Application of landslide progressive failure mechanical model based on the critical stress state
-
摘要: 边坡条分法物理意义是以强度折减表征材料峰值强度的下降程度。以不平衡推力部分强度折减法为例，推广传统假设，应用理想弹塑性模型和全过程剪应力-应变模型，在峰值剪应力和峰值应变相等条件下，模拟边坡的渐进破坏过程；提出了临界状态决定法，随着临界状态逐步移动，边坡不平衡力和驱动力越来越大，抗滑力越来越小，直至整体处于破坏状态。以湖北省恩施州稻池村边坡为例，以3种数值(部分强度折减、理想弹塑性和全过程剪应力-应变本构)模型揭示边坡渐进破坏过程中各参量变化特征。结果表明：3种数值条块法均能描述稻池村边坡渐进破坏过程，基于条分法和理想弹塑性模型部分强度折减系数大于全过程剪应力-应变本构模型稳定系数。Abstract: According to the physical significance of the slice method of slope, the strength softening behavior of the geo-material is characterized by strength reduction coefficient. The unbalanced thrust method hypothesis is generalized. And during the same state of peak shear stress and strain, the progressive failure process of landslide is simulated by using the perfect elastic-plastic model (PEPM) and the complete process shear stress-strain constitutive model (CPCM). Then, a determination method with critical stress state is proposed, and the partial strength reduction method (PSRM) is employed. The unbalance thrust force and driving sliding force become greater and greater, and the frictional resistance gets smaller and smaller during the deformation failure process. Taking the Daochicun landslide located in Enshi, Hubei Province as an example, the evolution characteristics in progressive failure process are revealed by the proposed method with three sorts of numerical simulations (PSRM, PEPM and CPCM). Results show that:the proposed generalized slice block method with the three numerical simulations can describe the progressive failure process of the landslide, the factor of safety of the PSRM and PEPM are more than that of the CPCM.
-
Key words:
- progressive failure /
- partial strength reduction method /
- constitutive model /
- slope
-
图 2 相连条块间应变及矢量关系图
Figure 2. Scheme of shear strain between slice blocks and its tensor relation
图 8 部分强度折减系数和剩余稳定系数关系
Figure 8. Relation of PSRM Fi and Fzsi with critical stress state slice block
图 9 临界条块为第12块时条块滑面力分布特征
Figure 9. Force distribution for the twelfth slice in the critical stress state
图 10 临界条块为第18块时条块滑面力分布特征
Figure 10. Force distribution for the eighteenth slice in the critical stress state
图 11 临界条块为第24块时条块滑面力分布特征
Figure 11. Force distribution for the twenty-forth slice in the critical stress state
-
[1] Fellenius W.Calculation of stability of earth dam[C]//Anon.Transactions: 2nd congress large dams.Washington, DC: [S.l.], 1936, 4: 445-462. [2] Bishop A W.The use of the slip circle in the stability analysis of slopes[J].Géotechnique, 1955, 5(1):7-17. doi: 10.1680/geot.1955.5.1.7 [3] Sarma S K, Tan D.Determination of critical slip surface in slope analysis[J].Géotechnique, 2006, 56(8):539-550. doi: 10.1680/geot.2006.56.8.539 [4] Kelesoglu M K.The evaluation of three-dimensional effects on slope stability by the strength reduction method[J].Ksce Journal of Civil Engineering, 2016, 20(1):1-14. http://d.wanfangdata.com.cn/periodical/5d824703afda941ac7d9b365be8994cd [5] Tiwari R C, Bhandary N P, Yatabe R.3D SEM approach to evaluate the stability of large-scale landslides in Nepal Himalaya[J].Geotechnical and Geological Engineering, 2015, 33(4):773-793. doi: 10.1007/s10706-015-9858-8 [6] 熊爽, 曾江波, 姚文敏, 等.降雨干湿循环作用下的渣土边坡稳定性[J].地质科技情报, 2018, 37(5):240-246. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzkjqb201805033 [7] Wei W B, Cheng Y M, Li L.Three-dimensional slope failure analysis by the strength reduction and limit equilibrium methods[J].Computers and Geotechnics, 2009, 36(1):70-80. http://www.sciencedirect.com/science/article/pii/S0266352X08000384 [8] Baker R.Nonlinear mohr envelopes based on triaxial data[J].Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(5):498-506. doi: 10.1061/(ASCE)1090-0241(2004)130:5(498) [9] Guo M, Ge X, Wang S.Slope stability analysis under seismic load by vector sum analysis method[J].Journal of Rock Mechanics and Geotechnical Engineering, 2011, 3(3):282-288. doi: 10.3724/SP.J.1235.2011.00282 [10] 卢应发, 杨丽平, 刘德富.一种新的节理本构模型及几种新的滑坡稳定系数计算方法[J].岩石力学与工程学报, 2013, 32(12):2431-2438. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb201312006 [11] 卢应发, 黄学斌, 刘德富.边坡力的分布特征和稳定性分析[J].岩土工程学报, 2017, 39(7):1321-1329. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ytgcxb201707019 [12] Lu Yingfa.Deformation and failure mechanism of slope in three dimensions[J].Journal of Rock Mechanics and Geotechnical Engineering, 2015, 7(2):109-119. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxyytgcxb-e201502001 -
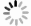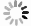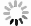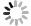
下载:
点击查看大图
图(12)
计量
- 文章访问数: 1022
- PDF下载量: 1152
- 被引次数: 0
