Abnormal event detection of city slope monitoring data based on multi-sensor information fusion
-
摘要: 为预防和管控城市突发地质灾害造成的人民生命和财产损失, 国家针对城市地质灾害易发地区部署了大量的各类传感器, 用来感知和监测城市边坡等地质体的变化情况, 以支持对地质灾害的预警。从边坡监测数据特点和时序数据分析技术出发, 针对监测数据噪声混杂、模式分析困难、预警阈值的不确定性等问题, 给出了一种基于多传感器信息融合的边坡监测数据异常事件检测方法。主要工作包括: ①边坡监测数据变化模式可以归结为周期项、趋势项以及噪声项的叠加, 实践中在预处理基础上对边坡监测数据进行周期为24 h的重采样, 同时趋势项可以近似看作是经典的牛顿运动, 以此构建形变运动模型, 为卡尔曼滤波的状态转移提供理论支持; ②采用集中式衰减记忆卡尔曼滤波, 引入衰减记忆因子, 对多传感器边坡监测数据进行特征级融合, 降低了噪声的影响, 提高了边坡监测数据的可靠性; ③引入惩罚系数, 应用改进的动态时间弯曲算法对于周期序列数据进行相似性度量。在此基础上基于K-means聚类和局部异常因子分析对边坡监测数据进行异常检测, 并基于3σ准则确定预警阈值。该方法能将正常模式和异常模式的时序数据进行区分, 有效检测出边坡监测数据的异常, 为灾害预防提供支持。最后以深圳市典型边坡监测数据为例验证了此方法的可行性。
-
关键词:
- 时序数据 /
- 多传感器信息融合 /
- 卡尔曼滤波 /
- 动态时间弯曲 /
- 边坡监测数据异常事件检测
Abstract: To prevent and control the loss of people's lives and property caused by sudden urban geological disasters, China has deployed a large number of sensors for urban geological disaster-prone areas to perceive changes in urban underground space. In this article, based on the characteristics of slope monitoring data and the analysis technology of time series data, aiming at problems such as noise mixtures in monitoring data, the difficulty of mode analysis and the uncertainty of early warning thresholds, a method of abnormal event detection in slope monitoring data based on multisensor information fusion is proposed. The results show that: ① Aiming at the disadvantage that the optimal estimation of the Kalman filter requires known noise information, the attenuation memory factor is introduced, and the centralized attenuation memory Kalman filter is used to fuse the multisensor slope monitoring data, which reduces the influence of noise and improves the reliability of slope monitoring data. ② The change mode of slope monitoring data can be summed up as the superposition of periodic term, trend term and noise term. The period is 24 hours, and the trend term can be approximately regarded as the classic Newtonian motion. Based on this, the deformation motion model can be constructed to provide theoretical support for the state transfer of the Kalman filter. ③ The penalty coefficient is introduced to make the improved DTW have a better measurement effect for the periodic sequence. On this basis, anomaly detection is carried out on the slope monitoring data based on K-means clustering, and local anomaly factors are used to analyse the abnormal conditions of the monitoring data. This method can distinguish the time series data of thenormal mode and abnormal mode better, detect abnormal slope monitoring data effectively, and provide guarantees for disaster prevention. Therefore, in view of the insufficiency of slope monitoring data processing and analysis processes, different information fusion technologies are adopted to improve the reliability and robustness of slope monitoring data. The feasibility of the proposed method is verified by slope monitoring data in Shenzhen. -
在众多的城市地质灾害中，由于滑坡地质灾害的突发性和复杂性，很难对其进行预防和管控。如何有效降低其造成的经济和人员损失，仍是一个亟待攻克的难关。在传感器、通讯和计算机技术支持下对城市边坡进行全面的自动化监测，同时开展边坡监测数据的挖掘和分析，从而达到实时管控及预警，对于城市安全运行和新型智慧城市建设具有重要意义[1-4]。
目前城市边坡监测技术已经从静态的人工监测转向了动态的、实时的自动化监测，从而满足对监测对象预警预报的准确性、及时性的要求[5]。边坡监测数据为典型的时序数据，具有高维、多源、异构、数据量大等特征。当数据存在异常模式时，可能表示着灾害孕育的前兆，对这些异常数据的进一步分析，有助于加深对边坡灾害发育过程的认识。目前，边坡自动化监测与信息融合技术相结合成为了一种新的发展趋势。例如，王腾军等[6]将GM(1, 1)模型与数据融合技术相结合，针对边坡形变量进行预测，以提高预测精度。侯圣山等[7]应用多传感器技术，对甘肃省3处较为危险的滑坡开展了监测预警，实现了对滑坡形变和环境因素的实时监控。智能算法的引入对边坡自动化监测产生了一定的作用，例如，王智伟等[8]对各种环境因子和滑坡位移变化量进行了显著性检查和筛选，选择影响较大的因子并使用BP神经网络对多源异构数据进行融合，认为该算法适用于滑坡变形预测。自适应卡尔曼滤波、基于位移参数等方法与多个位移传感器相结合，建立数据融合预测模型，不仅使得融合估计值更加准确，位移估计精度更高，而且还能够反映监测区的整体变化趋势[9-11]。
总体上，多传感器信息融合方法可概括为随机类和人工智能类两大类。随机类方法有加权平均法、卡尔曼滤波法、多贝叶斯估计法、证据推理、产生式规则等；而人工智能类方法则有模糊逻辑理论、神经网络、粗集理论、专家系统等[12]。信息融合过程中，异常模式的识别和分析对于边坡变形演化阶段的判别有着一定的辅助决策作用, 为此有不少学者展开了相关研究，例如，通过小波分析对滑坡演变过程中的突变异常点进行识别，分解后的信号在4个尺度上均表现出突变特征，以此可以作为突变的识别信号[13-14]。统计方法能够判断滑坡的位移变换规律，发现位移矢量角会随着边坡的失稳而出现相应异常，两者存在一定的相关性[15]。人工免疫思想与边坡稳定性预测相结合，或基于小样本在线自适应学习的异常检测技术，或基于人工神经网络(ANN)和模糊神经的预测技术等，均降低了建模的时间复杂度，提高了信息提取的效果[16-18]。但是，城市地质灾害监测数据处理与自动化监测技术的应用中仍然存在着一系列问题，例如数据可靠性差、模式分析困难、预警阈值的不确定性等。城市地质灾害监测数据的处理主要集中在位移形变有关数据受环境因素影响，监测的数据往往包含噪声，同时由于地质灾害的突发性和危险性，要求监测预警具备较高的实时性和准确性，为此笔者拟采用基于卡尔曼滤波的信息融合方法，该方法属于特征层的融合方法，不需大量的存储和计算开销，具备较高的实时性，融合结果的可靠性好，可以有效消除观测值中的噪声。针对于此，本研究思路是：结合城市边坡监测数据应用实际，重点研究数据预处理、信息融合、异常检测及预警等关键问题，先使用时序数据分析技术对监测数据进行处理，设计合适的相似性度量方法，在此基础上采用一种改进的集中式自适应卡尔曼滤波进行监测数据融合，最后采用基于概率统计的拉依达准则(3σ准则)(σ为标准差)对监测数据进行异常检测及预警。
1. 边坡数据的预处理
1.1 边坡数据预处理的方法
边坡监测方法通常包括：形变和位变(位移)监测、倾角监测、地下水位监测、降雨监测等。对所获得的一系列监测数据进行数据预处理，是提高数据融合和异常检测过程精度和性能的关键。对监测数据进行预处理，包括进行粗差检验和剔除、局部缺失的插补、平滑滤波去噪等操作。主要包含以下步骤[19]。
(1) 粗差的检验和剔除：粗差系指离群的误差，即奇异性误差。粗差无法从客观监测条件中寻找到合理性解释，其发生几率约为观察结果的1%~10%。粗差检验必须建立在一定准则的基础上，监测值若包含一个粗差，在对监测数据进行分析和预测之前需要进行粗差检验和剔除，以确保结果的正确性。通常包括原始监测数据的逻辑分析与原始监测数据的统计分析。逻辑分析以人工为主，而统计分析需要依据“3σ准则”进行剔除。
(2) 监测数据的插补：传感器所获取的数据，在时间变化上是连续的。后期数据处理过程中要求数据是等间隔的，因此需要对外界因素造成缺失的数据进行插补。通常采用线性插补的方法，其公式可以表示为：
y=f(t)+yi+1−yiti+1−ti(t−ti+1) (1) 式中：yi，yi+1均为监测值；t，ti+1均为采样时间。
(3) 监测数据平滑去噪：边坡的形变可以看成是趋势项和噪声项的结合，而去噪的目的就是为了消除信号中的噪声成分，提取出真实的形变值，从而提高后续数据融合、处理、分析的效果。通过小波变换，将信号分解成高频成分和低频成分，而噪声通常包含在高频成分中，通过构建门限阈值将高频成分中的噪声去除，最后通过逆变换将去除噪声的高频成分和低频成分进行重构，得到去噪信号。
(4) 监测系统中各个传感器的采样时间点和采样频率有所不同，这对于监测对象的观测是不同步的。需要对传感器所获取的异步监测数据进行配准，保证对监测对象的观测同步。通常是将不同时间间隔的传感器配准到一个采样间隔较长的传感器观测时间序列上，对于相同频率不同时刻的传感器，可以用插值拟合，近似拟合到同一观测时刻。
1.2 数据预处理实验与分析
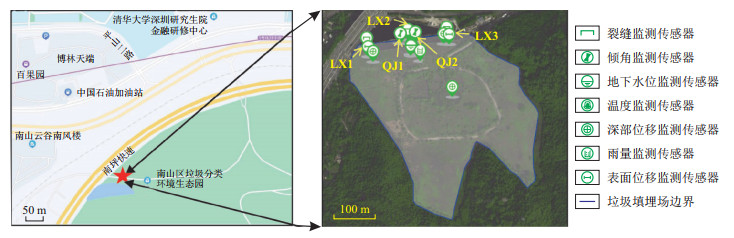
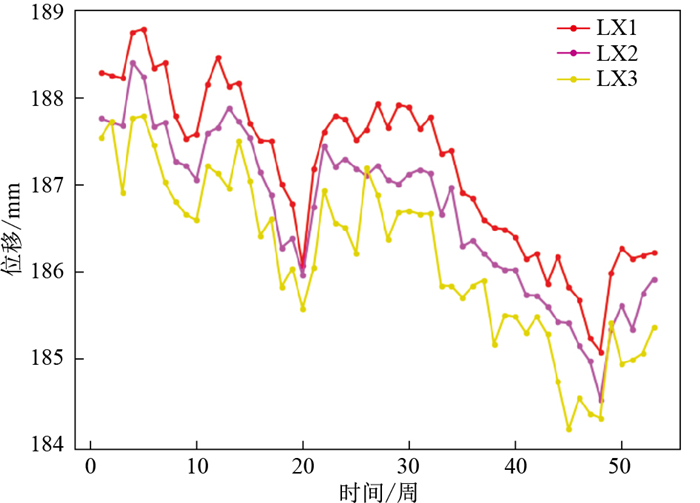
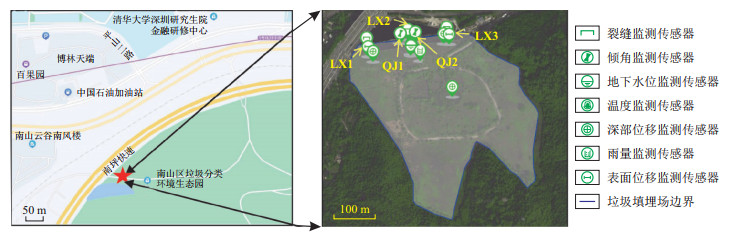
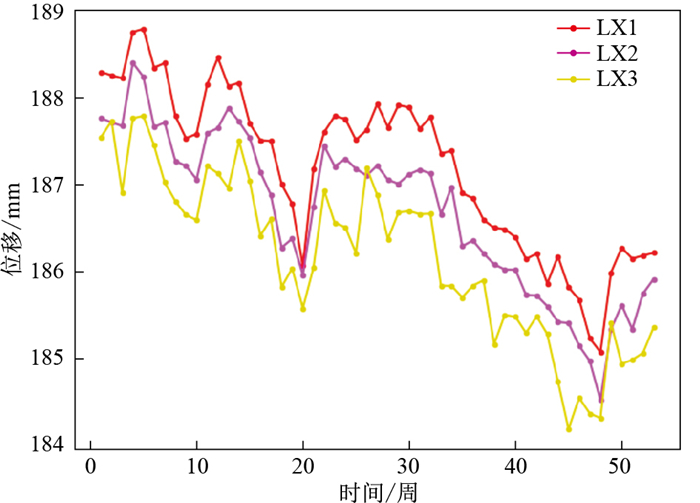
本研究的实验数据选自深圳市南山区平山垃圾填埋场北侧边坡的岩土体、挡土坝等监测数据。该填埋场位于塘朗山脚的山坳内，经过十多年的堆填目前已形成垃圾堆体边坡，填埋量达230万m3，为典型的城市人工堆填形成的边坡地带。为了边坡的安全管控，重点在边坡面向公路的北侧表面布设了裂缝监测点和表面水平位移监测点，同时在其垂直方向的不同深度布设了深部水平位移监测仪，进而共同监测边坡的水平位移和倾斜情况。此外，在地下水富集区布设了地下水位监测点和降雨量监测点。具体监测点位布置如图 1所示，图像中蓝色曲线圈部分为填埋场范围。这里采用边坡表面水平位移监测点LX1的监测数据作为实验数据，监测次数约290次，如表 1所示。
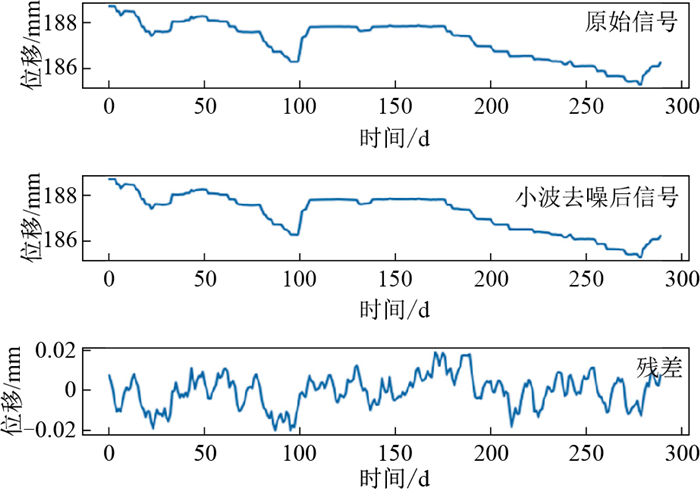
图 1 实验区传感器布置示意图Figure 1. Schematic diagram of the sensor layout in the experimental area表 1 边坡监测实验数据Table 1. Monitoring experimental data of the slope期数 位移量/mm 期数 位移量/mm 期数 位移量/mm 期数 位移量/mm 1 186.251 5 186.251 9 186.150 13 186.091 2 186.253 6 186.256 10 186.096 14 186.066 3 186.256 7 186.257 11 186.033 4 186.256 8 186.260 12 186.098 290 188.378 本研究釆用Daubechies小波[9]进行去噪，分解层数为3，阶数为10，阶数越大数据越平滑，并采用Python编程实现和进行计算处理，原始数据和去噪后数据对比图及残差图如图 2所示。
最后，通过计算模型的均方根(RMSE)、信号偏差(BIAS)和信噪比(SNR)对模型进行检验。均方根(RMSE)通过均方根误差大小来判断去噪效果，均方根误差越小，说明滤波效果越好。该模型去噪后计算得到RMSE=0.008 15。信号偏差(BIAS)表示去噪后估计信号与原始信号的偏差，偏差越接近于零越好。模型计算得到BIAS=0.006 4，非常接近于0。信噪比(SNR)越大说明信号中的噪声成分越小，则滤波效果越好。模型计算得到SNR=87.215。因此，使用Daubechies小波基对于高频率波动的数据进行去噪效果较好，但对非高频率波动的数据去噪反而可能丢失数据精度。
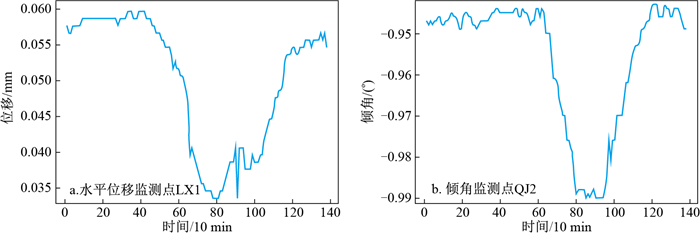
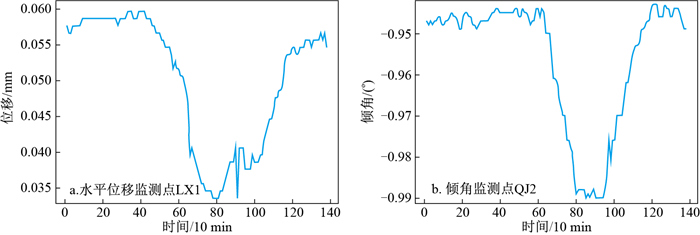
为了保证对监测目标观测数据的同步，需要对其进行时间配准。本研究使用的传感器的采样间隔均为10 min，部分传感器需要将其配准到同一时刻。本研究使用边坡表面水平位移监测点LX1以及倾角监测点QJ2于2021年2月24日的监测数据进行实验。数据如表 2所示，其对应的变化图像如图 3所示。
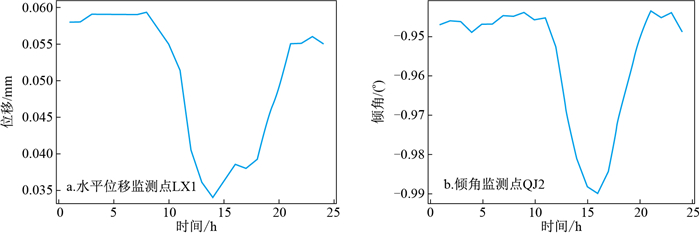
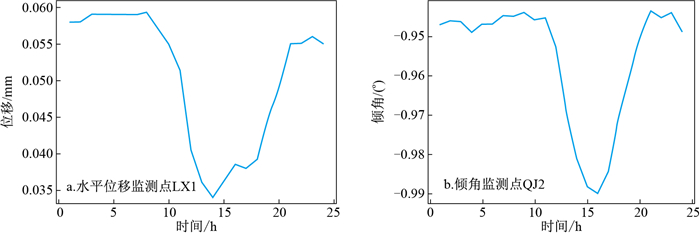
表 2 实验区水平位移监测点LX1及倾角监测点QJ2监测数据Table 2. Monitoring data of horizontal displacement and dip angle in monitoring area时间 LX1位移/mm 时间 QJ2倾角/(°) 00∶04∶31 186.258 00∶04∶43 -0.945 00∶14∶02 186.258 00∶15∶24 -0.947 00∶24∶44 186.257 00∶24∶57 -0.948 00∶35∶23 186.257 00∶35∶36 -0.947 00∶45∶00 186.258 00∶46∶20 -0.948 00∶56∶13 186.258 00∶54∶58 -0.947 23∶26∶28 186.257 23∶48∶30 -0.949 23∶36∶30 186.256 23∶59∶07 -0.949 23∶47∶06 186.257 23∶56∶44 186.255 
图 3 实验区水平位移监测点LX1(a)及倾角监测点QJ2(b)监测数据变化曲线Figure 3. Monitoring data of horizontal displacement LX1 (a) and dip angle QJ2 (b)分析观测数据可以发现，在当日LX1有138次采样，QJ2有136次采样，以10 min为采样周期，一天理论的采样次数应当为144次，由于各种原因，LX1数据缺失了6次，QJ2数据缺失了8次，同时由于初始采样时间点不同，随着时间的流逝，采样的时间点出现了偏移，从一开始采样的时间相差12 s，到当日的最后一个采样点相差了133 s，这种不同步的观测趋势必对后期处理分析造成影响。同时一天144次的采样次数，也会影响后期的运算效率，考虑到其在较短的时间内变化的幅度并不大，将其重采样至1次/h(即一天24次)为宜, 对2个传感器的监测数据进行配置得到的配准结果如图 4所示。
图 4 实验区水平位移监测点LX1(a)及倾角监测点QJ2(b)监测数据配准结果Figure 4. Registration results of the horizontal displacement LX1 (a) and dip angle QJ2 (b) monitoring data in monitoring area经过时间配准后，2个传感器的监测数据得到了同步，同时也消除了数据缺失带来的影响。由图 4可以看出两者的变化趋势大致相同，同时倾角相对于表面位移出现了一定的滞后，重采样也提升了后期算法运行的效率。
2. 多传感器边坡监测数据融合
2.1 基于集中式自适应卡尔曼滤波的数据融合
在监测系统中引入信息融合技术，可以补充有效信息量，提高测量精度与分辨率，增强特征提取效果。融合后的数据综合了多个传感器的数据信息，实现了信息互补，可以避免单一传感器数据导致的监测数据局部间断性、精度不足和信息不全面等问题。根据信息融合的处理信息所在的层次由低到高可以将信息融合分为：数据层融合、特征层融合、决策层融合[12]。
如前所述，卡尔曼滤波在边坡形变监测中已有广泛应用[9-11]。通过卡尔曼滤波，对边坡表面和深部部署的多个位移形变或其他类型传感器的信息进行融合，以得到边坡整体形变信息，从而对边坡的整体状况有一个全面的认知。实际应用中，标准的衰减记忆卡尔曼滤波虽然能在一定程度上抑制滤波器的发散，但是对于复杂的边坡结构仍不能满足其应用需求。为此，本研究采用一种集中式自适应卡尔曼滤波数据融合算法进行处理[11]，该算法简要介绍如下：
在第k个采样时刻，卡尔曼滤波算法定义残差序列为vk，如式(2)所示，其意义为真实值和测量值之间的误差。
v_{k}=\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k-1} (2) 式中：Zk为测量向量；Hk为测量矩阵； \hat{\boldsymbol{X}}_{k-1}为通过卡尔曼增益矩阵Kk计算得到后验估计。
由此可推其协方差满足：
E\left[\begin{array}{ll} v_{k} & v_{k}^{\mathrm{T}} \end{array}\right]=\boldsymbol{H}_{k} \boldsymbol{P}_{k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k} (3) 式中：Pk-1为误差协方差矩阵；Rk为观测噪声矩阵。
根据发散判断依据：
v_{k} v_{k}^{\mathrm{T}} \leqslant \gamma \cdot \operatorname{tr}\left[E\left(v_{k} \quad v_{k}^{\mathrm{T}}\right)\right] (4) 可得，当γ=1时有严格收敛判据，使用下式：
\boldsymbol{P}_{k}^{-}=\boldsymbol{A}\left(\lambda \boldsymbol{P}_{k-1}\right) \boldsymbol{A}^{\mathrm{T}}+\boldsymbol{Q} (5) 式中：A为状态转移矩阵；λ为自适应衰减记忆因子；Q为过程噪声矩阵。
替代式(3)中的Pk-1可得到：
\begin{aligned} E\left[\begin{array}{ll} v_{k} & v_{k}^{\mathrm{T}} \end{array}\right]=& \boldsymbol{H}_{k}\left[\boldsymbol{A}_{k}\left(\lambda \boldsymbol{P}_{k-1}^{*}\right) \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{Q}_{k-1}\right] \boldsymbol{H}_{k}^{\mathrm{T}}+\\ & \boldsymbol{R}_{k} \end{aligned} (6) 最后得到自适应衰减记忆因子λ为：
\lambda=\frac{v_{k}^{\mathrm{T}} v_{k}-\operatorname{tr}\left[\boldsymbol{H}_{k} \boldsymbol{Q}_{k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right]}{\operatorname{tr}\left[\boldsymbol{H}_{k} \boldsymbol{A}_{k} \boldsymbol{P}_{k-1}^{*} A_{k}^{\mathrm{T}} \boldsymbol{H}_{k}^{\mathrm{T}}\right]} (7) 随着监测技术与传感器观测精度的不断提高，测量误差也在逐步降低，传感器的观测值更加可靠，在衰减记忆卡尔曼滤波中通过增加新进测量值权重来遏制滤波器发散。这里在其基础上，通过限定记忆法进一步提高新进测量值权重，也就是说滤波器仅考虑最近N次测量，对于测量序列Z={Z1, Z2, …, Zk}，通过最近N次Zd, Zd+1, …, Zk来完成对X的估计，则带有限定记忆的卡尔曼滤波方程为：
\begin{aligned} \hat{\boldsymbol{X}}{}_{k}^{N}=& \boldsymbol{A}_{k, k-1} \hat{\boldsymbol{X}}{}_{k-1}^{N}+\boldsymbol{K}_{k}\left[\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \boldsymbol{A}_{k, k-1} \hat{\boldsymbol{X}}{}_{k-1}^{N}\right]-\\ & \overline{\boldsymbol{K}}_{k}\left[\boldsymbol{Z}_{d}-\boldsymbol{H}_{d} \boldsymbol{A}_{d, k} \boldsymbol{A}_{k, k-1} \hat{\boldsymbol{X}}_{k-1}^{N}\right] \end{aligned} (8) \boldsymbol{K}_{k}=\boldsymbol{P}_{k}^{N} \boldsymbol{H}_{k}^{\mathrm{T}} \boldsymbol{R}_{k}^{-1} (9) \overline{\boldsymbol{K}}_{k}=\boldsymbol{P}_{k}^{\mathrm{N}} \boldsymbol{A}_{d, k}^{\mathrm{T}} \boldsymbol{H}_{d}^{\mathrm{T}} \boldsymbol{R}_{d}^{-1} (10) \begin{aligned} \left(\boldsymbol{P}_{k}^{{N}}\right)^{-1}=& \boldsymbol{A}_{k-1, k}^{\mathrm{T}}\left(\boldsymbol{P}_{k-1}^{{N}}\right)^{-1} \boldsymbol{A}_{k-1, k}+\boldsymbol{H}_{k}^{\mathrm{T}} \boldsymbol{R}_{k}^{-1} \boldsymbol{H}_{k}-\\ &\boldsymbol{A}_{d, k}^{\mathrm{T}} \boldsymbol{H}_{d}^{\mathrm{T}} \boldsymbol{R}_{d}^{-1} \boldsymbol{H}_{d} \boldsymbol{A}_{d, k} \end{aligned} (11) 对于式(7)，依据过程噪声和观测噪声，实现了对卡尔曼增益的动态更新，使得改进的卡尔曼滤波具备更强的自适应性，通过限定记忆法，进一步加快了滤波器收敛速度，减少了系统不确定性对滤波器的影响，提高了最优估计值的精度和可靠性。
2.2 仿真实验与结果分析
使用Python语言编程进行仿真实验，进而验证算法的有效性。依据斋藤蠕变曲线模型，模拟生成边坡形变监测数据，将边坡形变量近似为经典牛顿运动模型，将边坡的形变位移和形变速率作为状态向量，建立边坡形变的运动模型如下：
\left\{\begin{array}{l} x(k+1)=x(k)+v_{x}(k) T+\frac{1}{2} w_{x}(k) T^{2} \\ y(k+1)=y(k)+v_{y}(k) T+\frac{1}{2} w_{y}(k) T^{2} \\ v_{x}(k+1)=v_{x}(k)+w_{x}(k) T \\ v_{y}(k+1)=v_{y}(k)+w_{y}(k) T \end{array}\right. (12) 式中: x(k)，y(k)为监测点的坐标；vx(k)，vy(k)分别为x和y方向上的速度；T为采样时间；w(k)为监测点的加速度。
边坡的形变状态方程可以表示如下：
\begin{gathered} {\left[\begin{array}{c} x(k+1) \\ y(k+1) \\ v_{x}(k+1) \\ v_{y}(k+1) \end{array}\right]=\left[\begin{array}{llll} 1 & 0 & T & 0 \\ 0 & 1 & 0 & T \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} x(k) \\ y(k) \\ v_{x}(k) \\ v_{y}(k) \end{array}\right]} \\ {\left[\begin{array}{cc} \frac{1}{2} T^{2} & 0 \\ 0 & \frac{1}{2} T^{2} \\ T & 0 \\ 0 & T \end{array}\right]\left[\begin{array}{l} w_{x}(k) \\ w_{y}(k) \end{array}\right]} \end{gathered} (13) 形变位移传感器的测量方程如下：
Z(k)=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right]\left[\begin{array}{c} x(k) \\ y(k) \\ v_{x}(k) \\ v_{y}(k) \end{array}\right]+v(k) (14) 式中：Z(k)为观测值；v(k)表示测量噪声。
对于卡尔曼滤波模型有:
\left\{\begin{array}{l} \boldsymbol{X}_{k}=\boldsymbol{A}_{k} \boldsymbol{X}_{k-1}+\boldsymbol{B} \boldsymbol{u}_{k-1}+\boldsymbol{W}_{k-1} \\ \boldsymbol{Z}_{k}=\boldsymbol{H}_{k} \boldsymbol{X}_{k}+\boldsymbol{V}_{k} \end{array}\right. (15) 对于式(15)有：
\begin{array}{l} \boldsymbol{A}_{k}=\left[\begin{array}{cccc} 1 & 0 & T & 0 \\ 0 & 1 & 0 & T \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right], \\ \boldsymbol{B}=\left[\begin{array}{cc} \frac{1}{2} T^{2} & 0 \\ 0 & \frac{1}{2} T^{2} \\ T & 0 \\ 0 & T \end{array}\right], \boldsymbol{W}_{k-1}=w(k) \end{array} (16) \boldsymbol{H}_{k}=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right], \boldsymbol{V}_{k}=v(k) (17) 初始化传感器监测点的坐标为[x(0), y(0)]T=[23.5, 8.96]T，初始化误差协方差矩阵为Px0=\left[\begin{array}{ll} 0.15 I & 0.2 I \\ -0.2 I & 0.1 I \end{array}\right] ，初始化系统测量噪声方差为1，采样时间间隔为1。假设\boldsymbol{A}=\left[\begin{array}{cc} I & 2 I \\ 0 & I \end{array}\right], \quad \boldsymbol{B}=\left[\begin{array}{l} 2 I \\ 2 I \end{array}\right] ， \boldsymbol{H}_{k}=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right]，对应的算法伪代码如下：
Algorithm 1: Improved centralized Kalman filter algorithm Inputs: A过程误差矩阵W B观测误差矩阵V C状态转移矩阵A D测量矩阵H E误差协方差矩阵P F初始状态向量X Algorithm steps 1 While Get(Lk) do 2 \hat{\boldsymbol{X}}_{k}^{-}=\boldsymbol{A} \hat{\boldsymbol{X}}_{k-1}+\boldsymbol{B} \boldsymbol{u}_{k-1} //预测 先验估计X 3 \boldsymbol{P}_{k}^{-}=\boldsymbol{A}\left(\lambda \boldsymbol{P}_{k-1}\right) \boldsymbol{A}^{\mathrm{T}}+\boldsymbol{Q} //预测 先验估计误差协方差 4 \boldsymbol{K}_{k}=\boldsymbol{P}_{k}^{-} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k}^{-} \boldsymbol{H}_{k}{}^{\mathrm{T}}+\boldsymbol{R}\right)-1 //校正 后验估计卡尔曼增益 5 \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}{}_{k}^{-}+\boldsymbol{K}_{k}\left[\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}{}_{k}^{-}\right] //校正 后验估计状态向量X 6 \boldsymbol{P}_{k}=\left[I-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right] \boldsymbol{P}_{k}^{-} //校正 后验估计误差协方差 7 End While Outputs: A最优估计状态向量\hat{X} 为了模拟真实环境下传感器受到的噪声干扰，在真实观测值的基础上，添加期望为0、方差为1的高斯白噪声，依据仿真模型得到的模拟数据如表 3所示，得到的数据融合结果如图 5所示。
表 3 仿真实验模拟数据Table 3. Simulation experiment data序号 真实值 传感器1测量值 传感器2测量值 融合值 1 25.003 24.519 24.527 24.570 2 25.038 24.829 26.115 25.254 3 25.055 26.308 25.166 25.712 4 25.127 24.303 25.867 25.457 5 24.977 24.414 24.335 24.894 6 24.818 24.314 24.808 24.677 48 32.456 258 67 31.489 33.981 32.569 49 32.911 428 72 32.389 34.334 33.258 50 33.593 419 76 33.824 33.252 33.723 统计分析传感器测量值和融合算法融合的最优估计值的均方根误差(RMSE)，如表 4所示。
表 4 不同方法的RMSETable 4. RMSE of different methods方法 RMSE 传感器1 0.710 2 传感器2 0.758 9 平均(传感器) 0.734 5 改进的自适应集中式卡尔曼滤波 0.335 8 可以看出采用改进的自适应集中式卡尔曼滤波数据融合算法，其仿真的融合数值与真实值更为接近，保留了原始数据的大部分信息，能够消除传感器的大部分噪声，相较于原始传感器观测值RMSE降低了54.25%。图 5中黑线为使用多传感器卡尔曼滤波算法进行数据融合得到的结果，相较于仅使用单一传感器，本研究提出的算法在处理过程中融合了多个传感器的信息，得到了当前时刻的最优估计值，融合的形变趋势更加贴合真实的形变趋势，且稳定性也较单一传感器更好。
2.3 边坡形变监测实验数据处理结果与分析
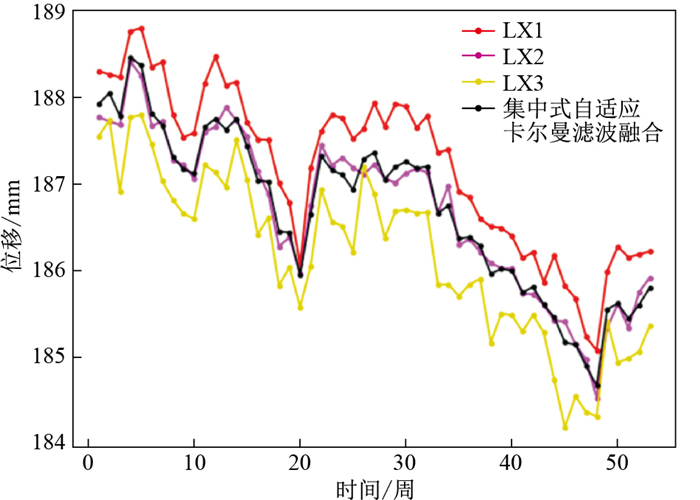
以深圳市的平山垃圾填埋场为例，监测项目现场共布设了20个传感器，其中包含3个边坡表面水平位移传感器(LX1，LX2，LX3)。每个传感器的采样间隔为1次/10 min，选取2020年3月-2021年3月的监测数据用于实验。为方便结果展示，对数据进行了重采样处理，采样频率调整至1次/1周，处理后得到了一年内53组边坡表面水平位移监测数据(表 5)，其对应的位移变化曲线如图 6所示。对这53组数据使用改进的集中式自适应卡尔曼滤波算法进行融合处理，分析近一年内边坡变形的情况。
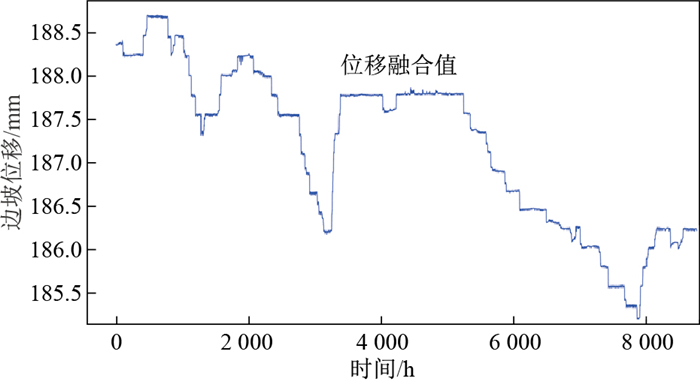
表 5 实验区3个边坡表面水平位移监测点的原始数据Table 5. Original data from three monitoring points in the experimental area位移/mm 监测日期 LX1 LX2 LX3 2020-03-18 188.294 187.763 187.543 2020-03-25 188.256 187.716 187.732 2020-04-01 188.224 187.674 186.910 2020-04-08 188.756 188.402 187.762 2020-04-15 188.792 188.239 187.790 2020-04-22 188.346 187.663 187.443 2020-04-29 188.745 187.861 187.542 2020-05-06 188.156 187.263 187.145 2021-03-03 186.147 185.333 184.981 2021-03-10 186.182 185.744 185.061 2021-03-17 186.214 185.912 185.355 
图 6 各水平位移监测点地表水平位移曲线Figure 6. Surface horizontal displacement curve of each monitoring point由图 6可以看出，各监测点的位移监测值随时间总体呈现出相同的变化趋势，反映出该监测区域的总体位移情况。不同时刻的位移监测值变化也有差异，可能由多种原因引起，例如地层本身物性或者结构的影响、传感器本身灵敏度的影响或是采样数据局部丢失等因素。使用改进的集中式自适应卡尔曼滤波算法对每个传感器的位移监测数据进行融合，得到的融合结果如图 7黑线所示。
图 7 各水平位移监测点地表水平位移及卡尔曼滤波数据融合结果曲线Figure 7. Surface horizontal displacement and Kalman filter data fusion curve of each monitoring point由图 7可以看出，在经过融合算法处理后，融合结果的形变曲线在一定的位移区间内波动，反映出该区域监测结果的总体变化趋势，且与各传感器的变化趋势吻合；此外，通过本研究的融合算法，对边坡不同位置的位移传感器所采集的数据进行融合，得到了边坡整体的水平位移最优估计值，提高了边坡水平位移监测数据的可靠性和观测精度，进一步消除了各种噪声的影响，为后续的数据挖掘与分析提供了可靠的数据支持。
3. 基于时间序列相似性度量的边坡监测数据异常检测
异常模式检测是数据挖掘与分析中重要的领域之一，目前该领域的主流算法分为以下4类[20]：①基于概率统计的算法，代表方法有3σ准则和马氏距离(Mahalanobis distance)；②基于最近邻的算法，其代表算法有KNN算法[20]、LOF算法等[21]；③基于聚类的算法，其代表算法有K-means、DBSCAN算法等；④基于分类的算法，属于有监督的方法，其代表算法有支持向量机、K近邻算法、决策树等，较为常用的算法是SVM算法[22]。目前，异常检测广泛应用于各个领域。上述不同的算法都有着各自的优缺点。基于概率统计的方法，当数据维度低时效果很好，其对模型的选取依赖度较高，具有较好的鲁棒性。基于距离的异常检测算法不需事先假设数据的分布，但是也不适用于高维数据，对于参数较为敏感，且无法检测出局部异常。基于聚类的异常检测算法，速度较快，可以实现实时检测，但检测效果依赖于聚类效果。异常检测算法的主要衡量指标是检测效率和检测准确率[23]，当前正朝着稳定性好、速度快、适用性强的方向发展。针对前面所述的这些问题，本研究将设计合适的相似性度量方法，在此基础上对监测数据进行分段并聚类，研究其变化模式，最后采用基于概率统计的拉依达准则对监测数据进行异常检测及预警。
3.1 基于改进DTW距离的边坡监测数据异常检测
3.1.1 带惩罚系数的DTW距离
在各类相似性度量方法中，动态时间弯曲(dynamic time warping，简称DTW)距离因其具备极强的鲁棒性而被广泛地应用于时间序列处理分析中，它能够解决欧式距离不能处理时序平移伸缩的问题，但边坡监测形变时间序列普遍存在波动大小不一、变化特征在时间跨度上没有对齐，造成采样时间间隔大小不一[24]。为改进DTW对周期序列度量不合理的缺点，引入惩罚系数，用以改善相似性度量，其求解过程[20]如下：
(1) 求解2个时序s1和s2的最长公共子串，长度记为a。由于s1和s2是数值型序列，存在一定的浮动偏差，在求最长公共子串时，设置了一个最大标准差的偏移容忍，当2个数值在标准差的容忍范围内时，也认为其是公共子串的一部分。
(2) 计算衰减系数： \alpha=1-\frac{a \times a}{\operatorname{len}\left(s_{1}\right) \times \operatorname{len}\left(s_{2}\right)}
3.1.2 LOF异常检测
使用局部异常因子(local outlier factor, 简称LOF)度量数据点的异常程度，LOF是一种基于局部密度的异常检测方法，其核心思想是异常数据点距离正常数据点较远，从而导致异常点周围的点较少，密度较低，也就是说LOF值越大，表示该数据点周围的数据点的密度越小，其为异常点的可能性越大。选用改进的DTW进行距离计算，通过LOF对边坡监测时间序列进行异常检测主要有5个步骤：①计算所有边坡形变时间序列的K近邻距离以及K近邻距离领域；②计算每个边坡形变时间序列的K近邻可达距离；③计算每个边坡形变时间序列的局部可达密度；④计算每个边坡形变时间序列的局部异常因子LOF值；⑤对LOF值进行排序，依据设定的阈值，输出λ个异常模式。
对于上述5个步骤，基于LOF边坡监测时间序列异常检测算法伪代码如下：
Algorithm 2:K-nearest neighbor local anomaly detection algorithm Inputs: A Timeseries TS B Number of nearest neighbors K Algorithm steps 1 L= len(TS); 2 for i in range(1, L) 3 for j in range(1, L) 4 if i!=j: 5 Data(i).add(point, dist(i, j)) 6 Sorted(Data(i)) 7 k-dist(p)= Data(i)[k][1] 8 for i in Data(i): 9 if Data(i)[1] < k-dist(p) 10 Nk(p).add(Data(i)[k][0]) 11 for i in range(1, L) 12 Data(i).lrd=getLrd 13 for i in range(1, L) 14 Data(i).lof=getLof Outputs: A Local Outlier Factor LOF 3.1.3 预警阈值选取方法
监测阈值主要通过设计计算结果、监测对象的相关规范规程、工程类比3种方法进行选取。基于3σ准则(拉依达准则)的边坡预警流程如下：①对历史监测数据进行分段，使用改进的DTW计算每段时间序列的LOF值；②统计LOF均值和标准差σ，得到安全区间[0, 3σ]；③监测数据新增时，计算其LOF并与安全区间所在范围进行比较，若超出区间范围，则将其视为异常并进行预警。
3.2 实验数据及结果分析
本研究以深圳市南山区的平山垃圾填埋场为例，并截选2020年2月29日-2021年2月27日的监测数据用以进行本次实验，反映出一个完整年度的变化情况。监测内容为：裂缝与边坡的表面位移、边坡深部水平位移、挡土坝倾角、地下水位与降雨量。本次实验所用的数据为表面水平位移数据，累积采集次数49 020次，采样频率为1次/10 min，共计365 d，表面水平位移情况如图 8所示。
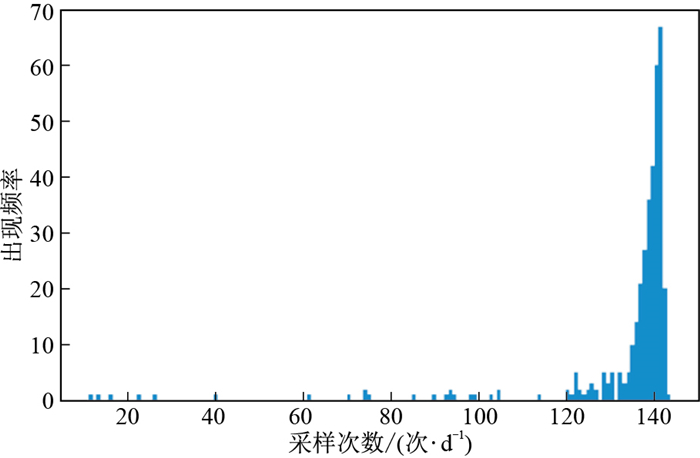
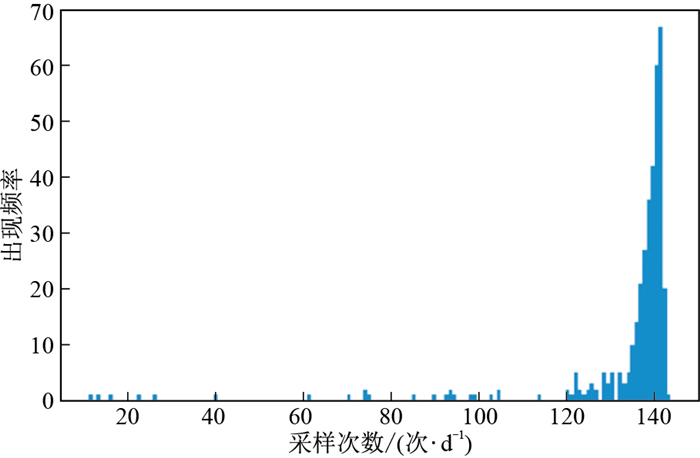
图 8 实验区边坡表面位移(近一年)Figure 8. Slope surface displacement in the experimental area(nearly one year)对每天的采样次数进行统计，得到的统计直方图如图 9所示。
从图 9中可以发现，大部分的采样次数大于120次，按每10 min采样一次，则一天所获得的采样次数应当为144次，这中间由于设备检修、传输等各种原因数据出现了缺失，考虑到数据在短时间内波动幅度不大，且前面发现了数据的变化周期为24 h，以日为单位，将每日获取的全部监测数据通过插值算法，重采样每日至24次，同时对数据进行归一化处理，从而降低数据维度，提高后续处理的效率。
3.2.1 K-means聚类分析以及LOF异常检测
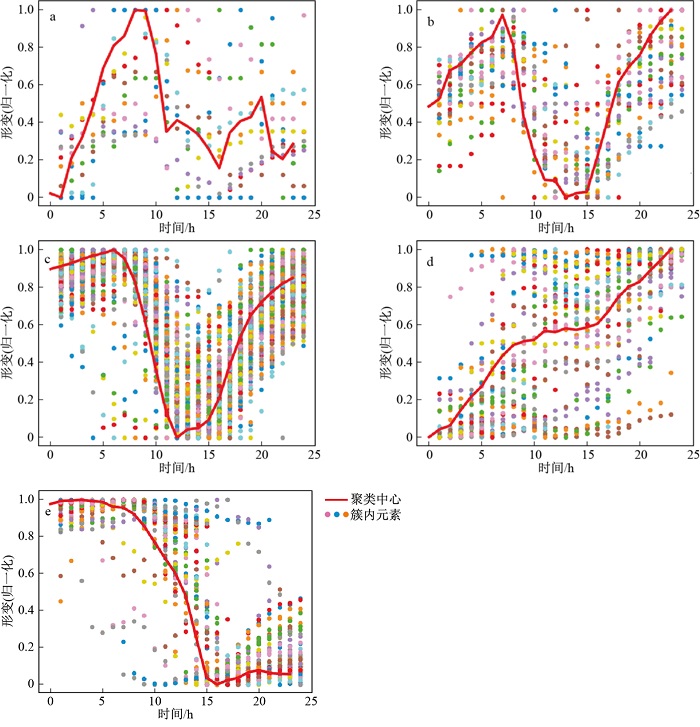
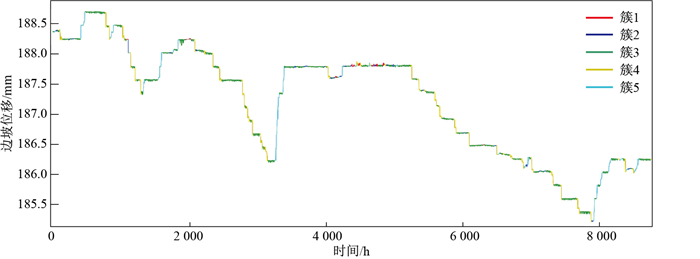
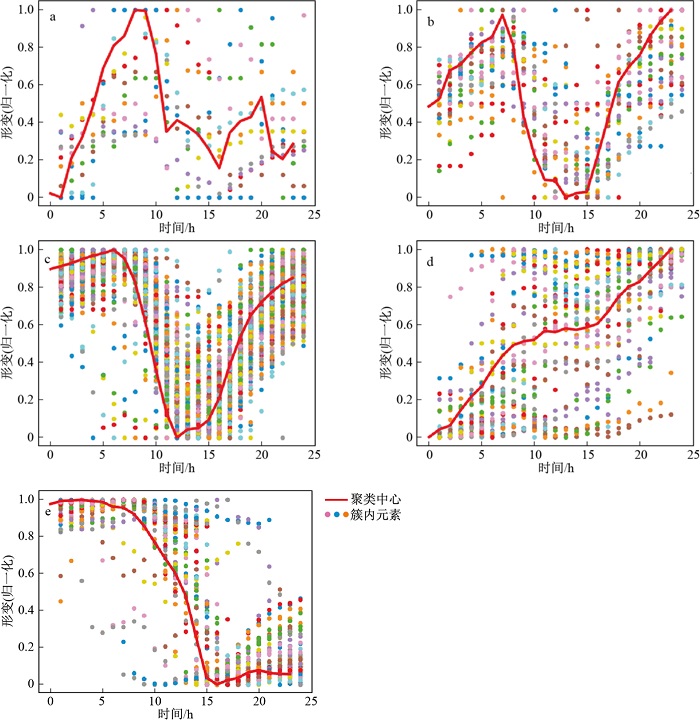
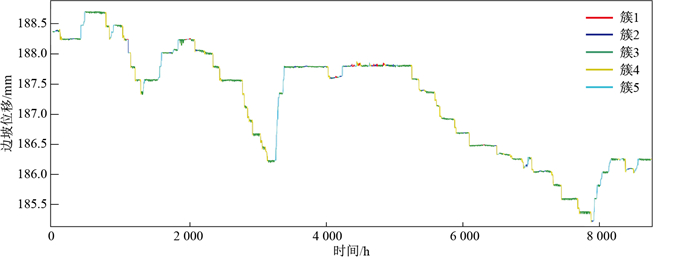
将数据从49 020条，重采样至365×24=8 760条，基于改进DTW距离，对数据进行K-means聚类，聚类个数设置为5，迭代次数设置为100，其中红色折线为每个簇的聚类中心，散点为该簇下的所有元素，得到的聚类结果如图 10中所示，每个簇的元素分别为11，27，230，58，39。
图 10 不同簇下的聚类结果a.簇1(11个元素)；b.簇2(27个元素)；
c.簇3(230个元素)；d.簇4(58个元素)；
e.簇5(39个元素)Figure 10. Clustering results under different clusters将聚类的结果投射在原始的时间序列数据上，得到的结果如图 11所示。
通过K-means将该时间段内的数据分成了5类，其中最大的簇类为簇3，共包含230个元素，其特征较为明显，为图 11中绿色标记的部分，表现为类正弦的周期变化；其次为簇4，有58个元素，其特征表现为日内的快速下行，形变幅度远超正常振幅，对应图 11中的黄绿色部分；簇5共有39个元素，其特征表现为日内快速上行，形变幅度远超正常振幅；再次为簇2，为淡蓝色部分，共有27个元素，其特征与簇3相似，不同之处在于其在日内的形变周期大致为簇3的1.5倍，起始于日内中值附近，上行至最大值后，再下行到最小值，最后再反弹到最大值；最后为簇1，有11个元素，没有明显的变化规律。整体上边坡的形变幅度在宏观上都是安全的，年累积形变幅度为3 mm, 在边坡监测的预警阈值可接受范围之内，因此簇3、簇4、簇5都是合理的变化模式，值得注意的是簇1和簇2，尤其是簇1其变化模式没有明显规律，与其他簇有着显著的区别。可以看到基于改进DTW距离度量的K-means聚类可以很好地将数据进行划分。
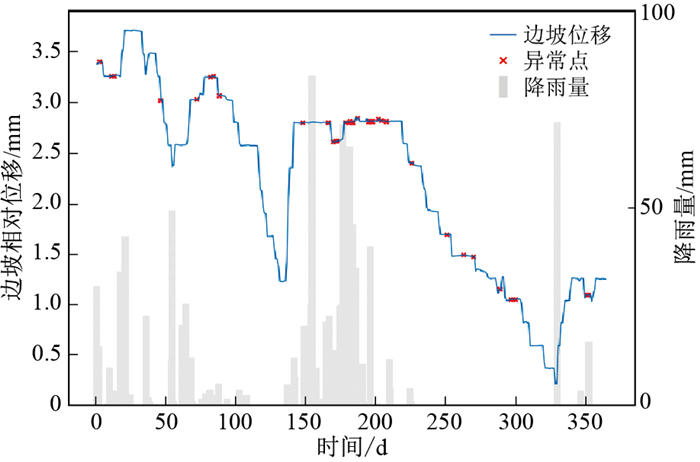
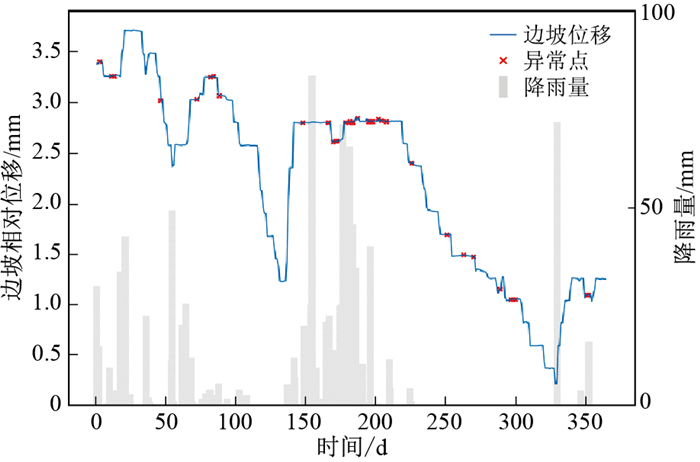
通过分析簇1和簇2的原始数据，以及历史降雨数据，发现簇1和簇2异常的原因大致可以归结为：降雨、数据缺失和未知原因3种类型。其中由降雨导致的异常事件居多，归纳降雨导致的地质异常事件日期主要包括2020年的3，6，7，8月，也存在着一些未知的异常事件，如：日期为“2020-10-05”处的异常等，需要进一步通过关联分析确认。
为了与实验区降雨量数据进行对比分析，将时间计算单位换算成天，对比结果如图 12所示，图中统计直方图代表日降雨量的分布。观察降雨与边坡表面位移异常可以发现，总体上有较好的对应关系，异常主要集中在降雨比较密集的6，7，8月份(本例中数据采集时间区间为2020年2月-2021年2月)。其他月份也存在异常(例如11月份)，关于这些异常存在的原因，需要进行其他因素的对比分析。
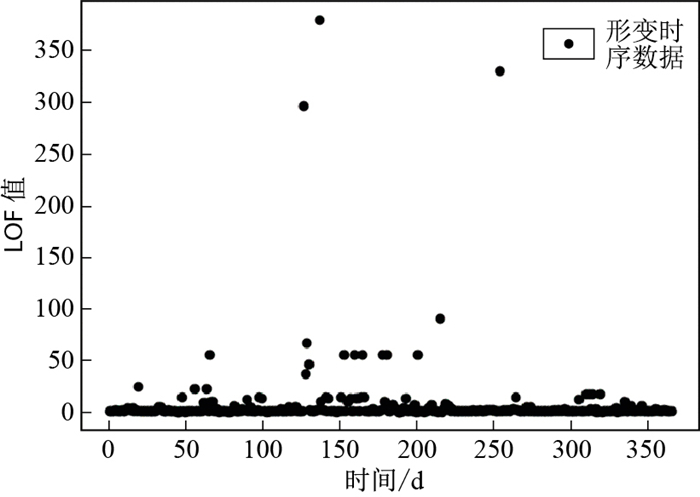
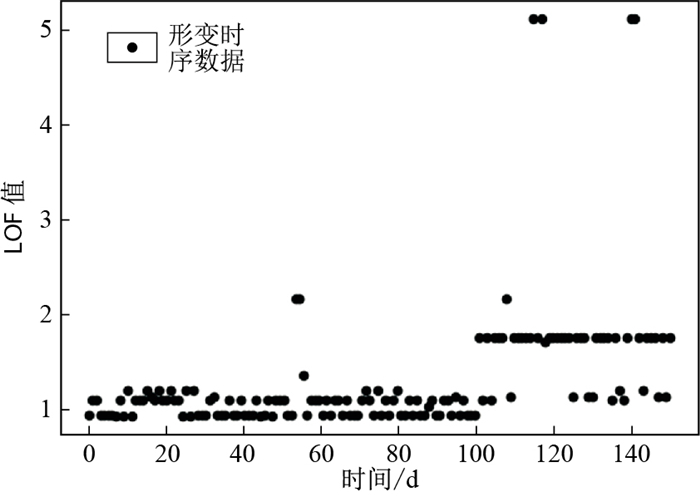
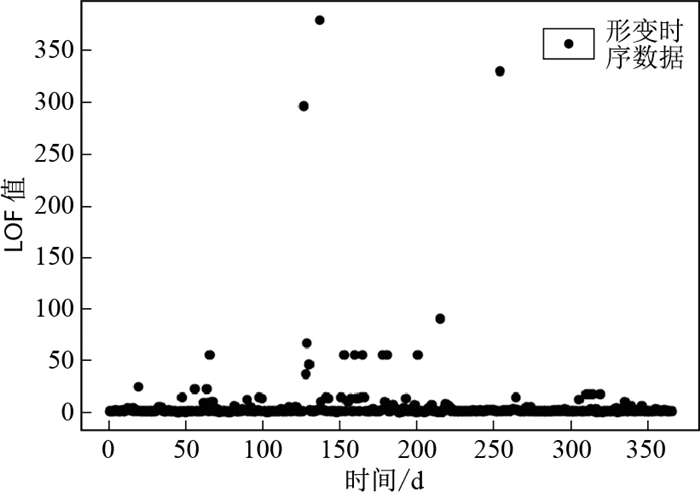
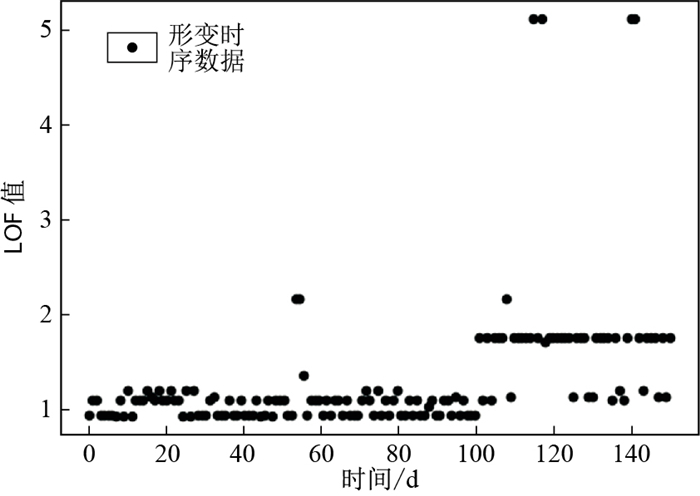
图 12 表面位移异常分布及日降雨量分布对比Figure 12. Comparison of surface displacement anomalies and daily rainfall试验中取k=10，使用LOF异常监测方法对时序数据进行异常检测，得到的结果如图 13所示，可以看出LOF较大的值主要集中在降雨较为密集的时间区间。
3.2.2 基于3σ准则的突变异常预警实验
本研究通过仿真模拟生成突变异常数据，以进行突变异常预警方法实验。突变异常仿真数据生成依据如下：①边坡从发现异常到失稳产生滑坡灾害的过程一般耗时仅数小时；②斋藤蠕变曲线模型；③《建筑边坡工程技术规范》(GB 50330-2013)。
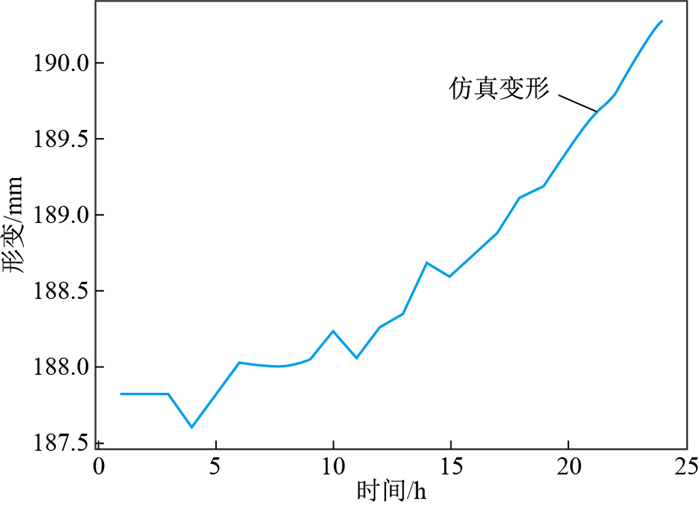
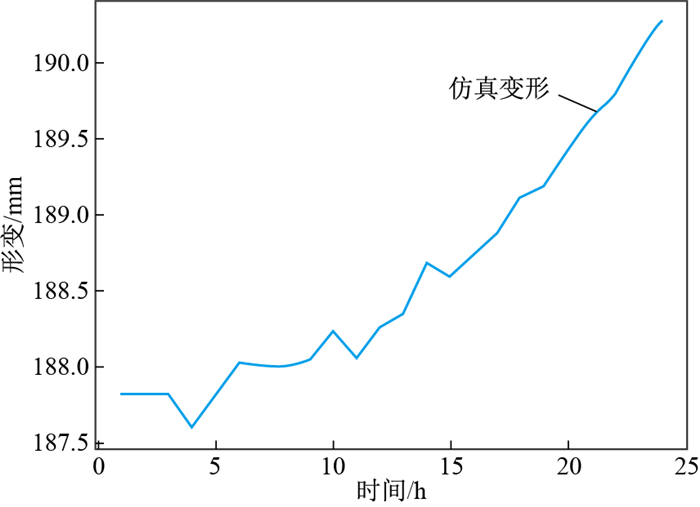
依据上述条件，实验的突变异常仿真数据生成步骤如下：①从全年的监测数据中随机选取一个时刻t，截取区间[t, t+24]的形变数据；②在形变区间上随机选取一点作为斋藤蠕变曲线模型中进入初加速阶段的突变异常点；③依据蠕变曲线模型在原有形变数据的基础上叠加加速形变阶段的形变值，以模拟边坡进入临滑阶段的形变，其累计形变幅度为四级预警阈值，以验证模型能否即时预警，从而开展防灾工作。
模拟仿真生成的突变异常数据变化模式如图 14所示。
在原有监测数据中选取100条数据作为正常形变数据，另外模拟仿真生成50条突变异常形变数据，组成共150条数据作为预警实验的数据集。在局部异常因子的基础上，依据拉依达准则(3σ准则)对形变数据进行异常检测。在正常的边坡监测数据中，发生滑坡的概率很小，因此可以认为突变异常为粗大误差。这种判别处理原理是以测量次数充分大为前提的，随着监测的不断进行，判别的精度会不断提高。对数据集进行局部异常因子计算，得到的结果如图 15所示，计算得到正常形变数据(即前100条数据)的LOF平均值为1.054 1，标准差为0.187，依据拉依达准则得到3σ值为1.054 1+0.187×3=1.615 1，则当LOF大于或等于该值时，我们将其视为异常，对比数据得到混淆矩阵如表 6所示。
图 15 仿真实验局部异常因子分析结果图(LOF≥1.615 1为异常)Figure 15. Result graph of the local anomaly factor of this simulation experiment(LOF≥1.615 1 for anomalies)表 6 混淆矩阵Table 6. Confusion matrix类别 正常 异常预警 正常(100) 98 2 异常(50) 12 38 本例中依据3σ准则通过计算可以得到基于LOF值的突变异常预警的总体准确率为73.3%，其中正常值的正确识别率98%，异常值的正确识别率76%。笔者提出的方法基于数理统计理论，不需要预先确定“阈值”，有助于解决阈值确定难题，具有实际意义。随着监测数据量的增加，或监测时间的增长，或传感器的个数增加，基于拉依达准则进行的异常预警准确率将进一步提高。
4. 结论与展望
(1) 通过分析发现边坡监测数据具有极强的周期性，其变化模式可以归结为周期项、趋势项以及噪声项的叠加。实践中在插补和配准等预处理基础上我们对边坡监测数据进行了周期为24 h的重采样，为后续数据处理降低维度，同时趋势项可以近似看作是经典的牛顿运动，以此构建形变运动模型，可以为卡尔曼滤波的状态转移提供理论支持。
(2) 针对基于单一传感器的数据处理与分析中数据可靠性较差的问题，采用改进的卡尔曼滤波方法融合多个传感器的数据进行信息互补，以提高监测系统的可靠性和鲁棒性。针对卡尔曼滤波最优估计需要已知噪声信息的缺点，引入了衰减记忆因子，采用集中式衰减记忆卡尔曼滤波，对多传感器边坡监测数据进行特征级融合，降低了噪声的影响，提高了边坡监测数据的可靠性。
(3) 引入惩罚系数，应用改进的DTW对于周期序列数据进行相似性度量，在此基础上基于K-means聚类和局部异常因子分析对边坡监测数据进行异常检测，并基于3σ准则确定预警阈值。实验结果表明，该方法能将正常模式和异常模式的时序数据进行区分，有效检测出边坡监测数据的异常，可以为灾害预警提供支持。依托深圳市典型边坡监测数据进行了方法可行性验证。
上述方法虽然形成了较为完整的边坡监测多传感器数据处理和分析集成应用方法，但以下方面的研究尚需进一步改进和深化：
(1) 虽然从边坡监测数据中检测出了异常，但是这些异常的原因有一部分尚不能得到很好的解释，而这些异常应当引起我们的重视，需要进一步分析这些异常模式产生的原因并改进不同类型传感器数据的关联融合算法，让我们对边坡的变化趋势有更深刻和更准确的认识。
(2) 基于改进的DTW相似性度量在计算过程中采用了动态规划的思想，时间开销较大，可以进一步对其进行改进以提升异常检测算法的效率。
(3) 不同类型传感器、不同频率监测和长期监测等数据的积累形成了边坡监测大数据，具有潜在的重要价值，有关智能处理方法和综合应用技术有待深入研究和开发。
深圳市地质局给予了监测数据和应用场景支持，在此深表谢意！ -
图 1 实验区传感器布置示意图
Figure 1. Schematic diagram of the sensor layout in the experimental area
图 3 实验区水平位移监测点LX1(a)及倾角监测点QJ2(b)监测数据变化曲线
Figure 3. Monitoring data of horizontal displacement LX1 (a) and dip angle QJ2 (b)
图 4 实验区水平位移监测点LX1(a)及倾角监测点QJ2(b)监测数据配准结果
Figure 4. Registration results of the horizontal displacement LX1 (a) and dip angle QJ2 (b) monitoring data in monitoring area
图 6 各水平位移监测点地表水平位移曲线
Figure 6. Surface horizontal displacement curve of each monitoring point
图 7 各水平位移监测点地表水平位移及卡尔曼滤波数据融合结果曲线
Figure 7. Surface horizontal displacement and Kalman filter data fusion curve of each monitoring point
图 8 实验区边坡表面位移(近一年)
Figure 8. Slope surface displacement in the experimental area(nearly one year)
图 10 不同簇下的聚类结果
a.簇1(11个元素)；b.簇2(27个元素)；
c.簇3(230个元素)；d.簇4(58个元素)；
e.簇5(39个元素)Figure 10. Clustering results under different clusters
图 12 表面位移异常分布及日降雨量分布对比
Figure 12. Comparison of surface displacement anomalies and daily rainfall
图 15 仿真实验局部异常因子分析结果图(LOF≥1.615 1为异常)
Figure 15. Result graph of the local anomaly factor of this simulation experiment(LOF≥1.615 1 for anomalies)
表 1 边坡监测实验数据
Table 1. Monitoring experimental data of the slope
期数 位移量/mm 期数 位移量/mm 期数 位移量/mm 期数 位移量/mm 1 186.251 5 186.251 9 186.150 13 186.091 2 186.253 6 186.256 10 186.096 14 186.066 3 186.256 7 186.257 11 186.033 4 186.256 8 186.260 12 186.098 290 188.378 
下载: 导出CSV
表 2 实验区水平位移监测点LX1及倾角监测点QJ2监测数据
Table 2. Monitoring data of horizontal displacement and dip angle in monitoring area
时间 LX1位移/mm 时间 QJ2倾角/(°) 00∶04∶31 186.258 00∶04∶43 -0.945 00∶14∶02 186.258 00∶15∶24 -0.947 00∶24∶44 186.257 00∶24∶57 -0.948 00∶35∶23 186.257 00∶35∶36 -0.947 00∶45∶00 186.258 00∶46∶20 -0.948 00∶56∶13 186.258 00∶54∶58 -0.947 23∶26∶28 186.257 23∶48∶30 -0.949 23∶36∶30 186.256 23∶59∶07 -0.949 23∶47∶06 186.257 23∶56∶44 186.255
下载: 导出CSV
Algorithm 1: Improved centralized Kalman filter algorithm Inputs: A过程误差矩阵W B观测误差矩阵V C状态转移矩阵A D测量矩阵H E误差协方差矩阵P F初始状态向量X Algorithm steps 1 While Get(Lk) do 2 \hat{\boldsymbol{X}}_{k}^{-}=\boldsymbol{A} \hat{\boldsymbol{X}}_{k-1}+\boldsymbol{B} \boldsymbol{u}_{k-1} //预测 先验估计X 3 \boldsymbol{P}_{k}^{-}=\boldsymbol{A}\left(\lambda \boldsymbol{P}_{k-1}\right) \boldsymbol{A}^{\mathrm{T}}+\boldsymbol{Q} //预测 先验估计误差协方差 4 \boldsymbol{K}_{k}=\boldsymbol{P}_{k}^{-} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k}^{-} \boldsymbol{H}_{k}{}^{\mathrm{T}}+\boldsymbol{R}\right)-1 //校正 后验估计卡尔曼增益 5 \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}{}_{k}^{-}+\boldsymbol{K}_{k}\left[\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}{}_{k}^{-}\right] //校正 后验估计状态向量X 6 \boldsymbol{P}_{k}=\left[I-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right] \boldsymbol{P}_{k}^{-} //校正 后验估计误差协方差 7 End While Outputs: A最优估计状态向量\hat{X}
下载: 导出CSV
表 3 仿真实验模拟数据
Table 3. Simulation experiment data
序号 真实值 传感器1测量值 传感器2测量值 融合值 1 25.003 24.519 24.527 24.570 2 25.038 24.829 26.115 25.254 3 25.055 26.308 25.166 25.712 4 25.127 24.303 25.867 25.457 5 24.977 24.414 24.335 24.894 6 24.818 24.314 24.808 24.677 48 32.456 258 67 31.489 33.981 32.569 49 32.911 428 72 32.389 34.334 33.258 50 33.593 419 76 33.824 33.252 33.723
下载: 导出CSV
表 4 不同方法的RMSE
Table 4. RMSE of different methods
方法 RMSE 传感器1 0.710 2 传感器2 0.758 9 平均(传感器) 0.734 5 改进的自适应集中式卡尔曼滤波 0.335 8
下载: 导出CSV
表 5 实验区3个边坡表面水平位移监测点的原始数据
Table 5. Original data from three monitoring points in the experimental area
位移/mm 监测日期 LX1 LX2 LX3 2020-03-18 188.294 187.763 187.543 2020-03-25 188.256 187.716 187.732 2020-04-01 188.224 187.674 186.910 2020-04-08 188.756 188.402 187.762 2020-04-15 188.792 188.239 187.790 2020-04-22 188.346 187.663 187.443 2020-04-29 188.745 187.861 187.542 2020-05-06 188.156 187.263 187.145 2021-03-03 186.147 185.333 184.981 2021-03-10 186.182 185.744 185.061 2021-03-17 186.214 185.912 185.355
下载: 导出CSV
Algorithm 2:K-nearest neighbor local anomaly detection algorithm Inputs: A Timeseries TS B Number of nearest neighbors K Algorithm steps 1 L= len(TS); 2 for i in range(1, L) 3 for j in range(1, L) 4 if i!=j: 5 Data(i).add(point, dist(i, j)) 6 Sorted(Data(i)) 7 k-dist(p)= Data(i)[k][1] 8 for i in Data(i): 9 if Data(i)[1] < k-dist(p) 10 Nk(p).add(Data(i)[k][0]) 11 for i in range(1, L) 12 Data(i).lrd=getLrd 13 for i in range(1, L) 14 Data(i).lof=getLof Outputs: A Local Outlier Factor LOF
下载: 导出CSV
-
[1] 吴冲龙, 刘刚, 王力哲, 等. 基于大数据的城市地质环境智能监管思路与方法[J]. 地质科技通报, 2020, 39(1): 157-163. doi: 10.19509/j.cnki.dzkq.2020.0117Wu C L, Liu G, Wang L Z, et al. Thinking and methods of intelligent supervision of urban geological environment based on big data[J]. Bulletin of Geological Science and Technology, 2020, 39(1): 157-163(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0117 [2] 刘军旗, 刘强, 刘千慧, 等. 大数据时代地质灾害数据管理及应用模式探讨[J]. 地质科技通报, 2021, 40(6): 276-282, 292. doi: 10.19509/j.cnki.dzkq.2021.0627Liu J Q, Liu Q, Liu Q H, et al. Discussion of geological hazard data management and application model in big data era[J]. Bulletin of Geological Science and Technology, 2021, 40(6): 276-282, 292(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2021.0627 [3] 许强. 对滑坡监测预警相关问题的认识与思考[J]. 工程地质学报, 2020, 28(2): 360-374. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202002017.htmXu Q. Understanding the landslide monitoring and early warning: Consideration to practical issues[J]. Journal of Engineering Geology, 2020, 28(2): 360-374(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202002017.htm [4] 仝德富, 谭飞, 苏爱军, 等. 基于多源数据的谭家湾滑坡变形机制及稳定性评价[J]. 地质科技通报, 2021, 40(4): 162-170. doi: 10.19509/j.cnki.dzkq.2021.0432Tong D F, Tan F, Su A J, et al. Deformation mechanism and stability evaluation of Tanjiawan landslide based on multi-source data[J]. Bulletin of Geological Science and Technology, 2021, 40(4): 162-170(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2021.0432 [5] 熊寄然. GNSS技术在城市边坡监测中的应用[J]. 重庆建筑, 2019, 18(8): 47-49. https://www.cnki.com.cn/Article/CJFDTOTAL-CQJZ201908021.htmXiong J R. Application of GNSS technology in urban slope monitoring[J]. Chongqing Architecture, 2019, 18(8): 47-49(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-CQJZ201908021.htm [6] 王腾军, 赖百炼, 叶俊华, 等. 基于GM(1, 1)数据融合算法的滑坡预测研究[J]. 测绘通报, 2012(5): 63-65. https://www.cnki.com.cn/Article/CJFDTOTAL-CHTB201205021.htmWang T J, Lai B L, Ye J H, et al. Research on landslide prediction based on GM(1, 1) data fusion algorithm[J]. Bulletin of Surveying and Mapping, 2012(5): 63-65(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-CHTB201205021.htm [7] 侯圣山, 李昂, 陈亮, 等. 基于普适型仪器的滑坡监测预警初探: 以甘肃兰州岷县三处滑坡为例[J]. 中国地质灾害与防治学报, 2020, 31(6): 47-53. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDH202006006.htmHou S S, Li A, Chen L, et. al. Application of universal geo-hazard monitoring instruments in landslides and early warning of three landslides in Gansu Province: A case study in Minxian County and Lanzhou City of Gansu Province[J]. The Chinese Journal of Geological Hazard and Control, 2020, 31(6): 47-53(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDH202006006.htm [8] 王智伟, 王利, 黄观文, 等. 基于BP神经网络的滑坡监测多源异构数据融合算法研究[J]. 地质力学学报, 2020, 26(4): 575-582. https://www.cnki.com.cn/Article/CJFDTOTAL-DZLX202004014.htmWang Z W, Wang L, Huang G W, et al. Research on multi-source heterogeneous data fusion algorithm of landslide monitoring based on BP neural network[J]. Journal of Geomechanics, 2020, 26(4): 575-582(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZLX202004014.htm [9] 刘超云, 尹小波, 张彬. 基于Kalman滤波数据融合技术的滑坡变形分析与预测[J]. 中国地质灾害与防治学报, 2015, 26(4): 30-35. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDH201504007.htmLiu C Y, Yin X B, Zhang B. Analysis and prediction of landslide deformations based on data fusion technology of Kalman-filter[J]. The Chinese Journal of Geological Hazard and Control, 2015, 26(4): 30-35(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDH201504007.htm [10] 张福荣. 自适应卡尔曼滤波在变形监测数据处理中的应用研究[D]. 西安: 长安大学, 2009.Zhang F R. Application of adaptive kalman filter in deformation monitoring data processing[D]. Xi'an: Chang'an University, 2009(in Chinese with English abstract). [11] 朱自强, 吴顺川, 刘洋, 等. 基于自适应Kalman滤波融合技术的边坡变形分析[J]. 矿业研究与开发, 2020, 40(1): 16-21. https://www.cnki.com.cn/Article/CJFDTOTAL-KYYK202001004.htmZhu Z Q, Wu S C, Liu Y, et al. Slope deformation analysis based on adaptive Kalman-filter fusion technology[J]. Mining Research and Development, 2020, 40(1): 16-21(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-KYYK202001004.htm [12] 吴艳. 多传感器数据融合算法研究[D]. 西安: 西安电子科技大学, 2003.Wu Y. Study of multisensor data fusion algorithms[D]. Xi'an: Xidian University, 2003(in Chinese with English abstract). [13] Novikov I Y. Asymptotics of the roots of bernstein polynomials used in the construction of modified daubechies wavelets[J]. Mathematical Notes, 2002, 71(1): 217-229. [14] 李秀珍. 滑坡变形突变异常的小波识别方法[J]. 自然灾害学报, 2015, 24(6): 50-56. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH201506006.htmLi X Z. Wavelet identification method for deformation abnormality of landslides[J]. Journal of Natural Disasters, 2015, 24(6): 50-56(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH201506006.htm [15] 李新源, 贺可强, 贾玉跃, 等. 堆积层滑坡位移矢量角异常变化分析: 以新滩滑坡为例[J]. 价值工程, 2010, 29(17): 88-89. https://www.cnki.com.cn/Article/CJFDTOTAL-JZGC201017060.htmLi X Y, He K Q, Jia Y Y, et al. Analysis on the displacement vector angle abnormal of colluvial landslide: Xintan landslide as an example[J]. Value Engineering, 2010, 29(17): 88-89(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JZGC201017060.htm [16] 袁勇, 许强, 陈聆. 基于人工免疫算法的数据压缩技术在滑坡异常提取中的应用研究[J]. 成都理工大学学报: 自然科学版, 2007, 34(6): 621-625. https://www.cnki.com.cn/Article/CJFDTOTAL-CDLG200706008.htmYuan Y, Xu Q, Chen L. Application of data compression based on AIS to the extraction of landslide anomaly[J]. Journal of Chengdu University of Technology: Science & Technology Edition, 2007, 34(6): 621-625(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-CDLG200706008.htm [17] Li D, Liu S, Zhang H. A boundary-fixed negative selection algorithm with online adaptive learning under small samples for anomaly detection[J]. Engineering Applications of Artificial Intelligence, 2016, 50: 93-105. doi: 10.1016/j.engappai.2015.12.014 [18] Safa M, Sari P A, Shariati M, et al. Development of neuro-fuzzy and neuro-bee predictive models for prediction of the safety factor of eco-protection slopes[J]. Physica A: Statistical Mechanics and Its Applications, 2020, 550: 124046. [19] 陈小惠, 万德钧, 王庆. 模糊逻辑在分布式多目标跟踪融合中的应用研究[J]. 东南大学学报: 自然科学版, 2003, 33(6): 754-757. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX200306017.htmChen X H, Wan D Y, Wang Q. Study for distributed multitarget tracking fusion using fuzzy logic[J]. Journal of Southeast University: Natural Science Edition, 2003, 33(6): 754-757(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX200306017.htm [20] 卢鋆, 吴忠望, 王宇, 等. 基于KNN算法的异常行为检测方法研究[J]. 计算机工程, 2007, 33(7): 133-134, 138. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJC200707048.htmLu Y, Wu Z W, Wang Y, et al. Research on abnormal behavior detection based on KNN algorithm[J]. Computer Engineering, 2007, 33(7): 133-134, 138(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJC200707048.htm [21] Breunig M M, Kriegel H P, Raymond T N, et al. LOF: Identifying density-based local outliers[C]//Proc. ACM SIGMOD Int. Conf. on Management of Data. Dalles, TX, USA: [s. n. ], 2000: 1-12. [22] 武小年, 彭小金, 杨宇洋, 等. 入侵检测中基于SVM的两级特征选择方法[J]. 通信学报, 2015, 36(4): 23-30. https://www.cnki.com.cn/Article/CJFDTOTAL-TXXB201504003.htmWu X N, Peng X J, Yang Y Y, et al. Two-level feature selection method based on SVM for intrusion detection[J]. Journal on Communications, 2015, 36(4): 23-30(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-TXXB201504003.htm [23] 王思敬, 杨志法, 刘竹华. 地下工程岩体稳定分析[M]. 北京: 科学出版社, 1984.Wang S J, Yang Z F, Liu Z H. Stability analysis of underground engineering rock mass[M]. Beijing: Science Press, 1984(in Chinese). [24] Thuy H, Anh D T, Chau V. Efficient segmentation-based methods for anomaly detection in static and streaming time series under dynamic time warping[J]. Journal of Intelligent Information Systems, 2021, 56(3): 121-146. 期刊类型引用(9)
1. 张磊，巨能攀，何朝阳，解明礼，张成强，刘洋. 滑坡裂缝计时序数据实时异常检测分析. 岩石力学与工程学报. 2024(01): 206-215 . 
百度学术2. 李瑞晨，侯木舟，孔梦麟，谢昊含. 基于VMD-SegSigmoid-XGBoost-ClusterLSTM算法的山体滑坡表面位移预测. 科技通报. 2024(09): 111-115 . 百度学术3. 陈明月 ，辛家昭 ，郜海明 ，于德水 ，苟海东 . 联合卡尔曼滤波下基坑施工竖向位移监测数据融合方法. 建筑机械. 2024(12): 184-190 . 百度学术4. 肖自为，马源，李金林，龚弦，邓修林，程曦. 基于过程预警模型的矿山边坡监测系统研究与应用. 地质灾害与环境保护. 2024(04): 91-98 . 百度学术5. 郭传臣，杨敏. 基于光纤传感器的铁路工程边坡形变检测研究. 工程建设与设计. 2023(12): 104-106 . 百度学术6. 王金锟. 基于物联网的智慧教室环境多传感器节点数据自适应融合方法. 桂林航天工业学院学报. 2023(02): 226-231 . 百度学术7. 李东昆，高险峰，张乃平，卢宇亭. 基于改进K-means算法的光通信数据异常检测预警方法. 自动化与仪器仪表. 2023(07): 51-54 . 百度学术8. 陈根深，刘刚，陈麒玉，赵力行，向世泽，罗庆，张俊杰. 基于多源数据集成与WebGIS的三维矿山空间数据管理系统关键技术及应用. 软件导刊. 2023(11): 18-28 . 百度学术9. 施宝海. 基于传感器信息融合的自动扶梯电机运行监控技术. 设备管理与维修. 2023(22): 43-45 . 百度学术其他类型引用(5)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 1825
- PDF下载量: 187
- 被引次数: 14
