基于Hoek-Brown准则的节理岩体能量参数估算

柴波; 陶阳阳; 杜娟; 台大平; 王禹

doi:10.19509/j.cnki.dzkq.2020.0109

基于Hoek-Brown准则的节理岩体能量参数估算

doi: 10.19509/j.cnki.dzkq.2020.0109

柴波^1a,,
陶阳阳^1a,
杜娟^1b,
台大平²,
王禹^1a

基金项目:

国家自然科学基金项目 41572256

国家自然科学基金项目 41877253

中央高校基本科研业务费专项资金资助项目 CUGL160408

详细信息

作者简介:
柴波(1981-), 男, 教授, 博士生导师, 主要从事环境地质和工程地质方面的教学与研究工作。E-mail:chabo@cug.edu.cn

中图分类号: P642
计量
- 文章访问数: 617
- PDF下载量: 3423
- 被引次数: 0
出版历程
- 收稿日期: 2019-11-27

Energetics parameter estimation of jointed rock mass based on Hoek-Brown failure criterion

Chai Bo^{1a
,},
Tao Yangyang^1a,
Du Juan^1b,
Tai Daping²,
Wang Yu^1a

摘要

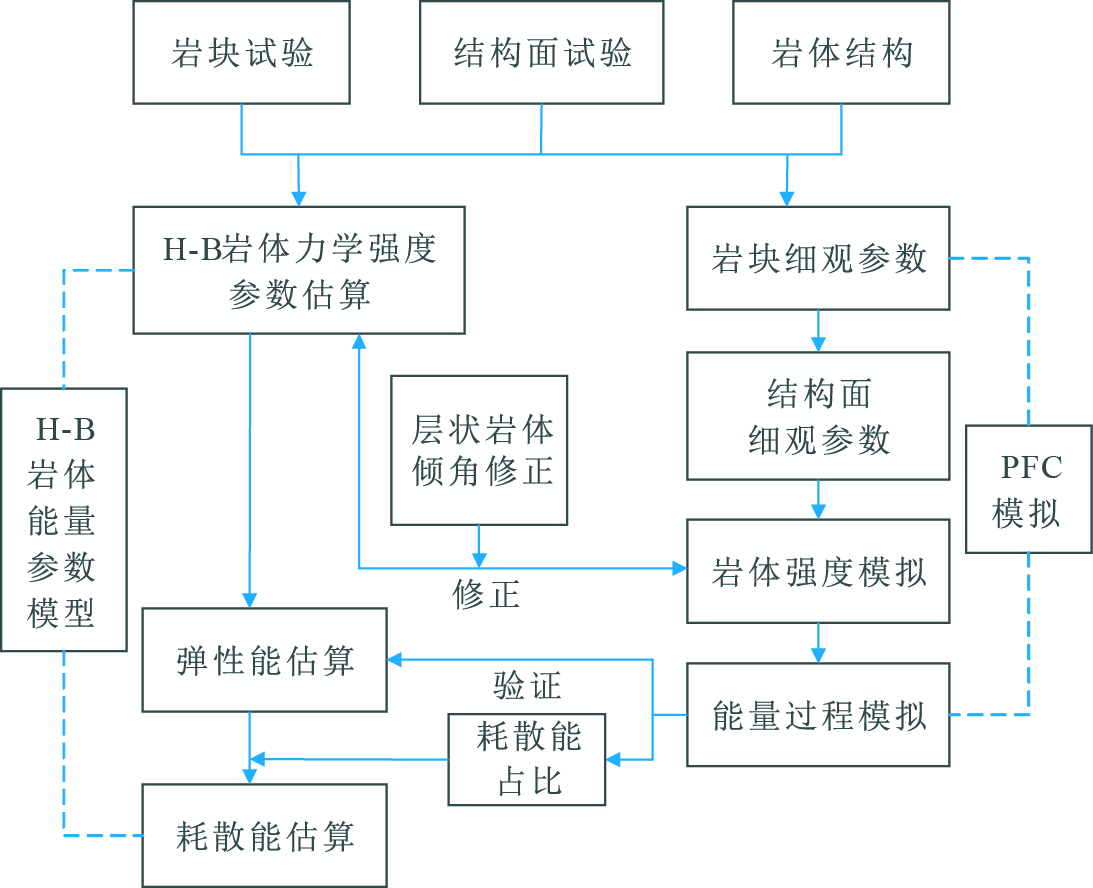
摘要: 岩体变形和破坏可以看作能量耗散和释放的过程。由于节理岩体结构复杂且难以开展室内试验，因此无法通过试验直接求取其能量学参数。基于Hoek-Brown准则和岩石能量理论，提出了节理岩体在临界状态能量学参数的估算方法。针对含贯通节理（或层面）岩体，通过修正岩块单轴抗压强度以体现贯通节理的方向效应。采用PFC^3D分别模拟小尺寸岩样（Φ50 mm×100 mm）和大尺寸岩体（Φ2 m×2 m）的三轴压缩试验，通过岩石三轴试验结果拟合岩石数值模拟的细观参数并应用于节理岩体的模拟。根据节理岩体模拟得到应力应变曲线和能量流，验证了Hoek-Brown准则对节理岩体能量参数估算的合理性。
- 岩体能量参数 /
- 三轴压缩试验 /
- 数值模拟 /
- 节理岩体
Abstract: The deformation and failure of rocks are a process of energy dissipation and release. For the jointed rock masses, the estimation of energetics parameters during loading procedures is a challenge because of their complex structures and difficulties of laboratory tests. The paper proposed a methodology for the energetics parameter estimation of jointed rock masses in critical state based on the Hoek-Brown failure criterion and rock energy theory. For the rock mass with continuous joints (or layers), the orientation effect of continuous joints was reflected by the revised uniaxial compressive strength of rock piece. The PFC^3Dnumerical simulation software was used to simulate the triaxial compressive process with small size models of rock pieces (Φ50 mm×100 mm) and big size models of rock masses (Φ2 m×2 m). The mesoscopic parameters of rock numerical model were calibrated by the result of triaxial compression test and applied for the numerical simulation of jointed rock mass. The estimated energetics parameters derived from Hoek-Brown failure criterion were proved to be accurate by the validation with simulated stress strain curves and energy curves.
- energetics parameters of rock mass /
- triaxial compressive test /
- numerical simulation /
- jointed rock mass

HTML全文

图 1 研究思路

Figure 1. Flow chart

下载: 全尺寸图片幻灯片

图 2 三轴循环加载试验下应力-应变曲线及模拟曲线

Figure 2. The stress-strain curves of triaxial cyclic loading test and the simulated curves of PFC

下载: 全尺寸图片幻灯片

图 3 含贯通节理岩体轴向应力应变曲线及能量流

Figure 3. The simulated axial stress and energy variation of layered rock masses

下载: 全尺寸图片幻灯片

图 4 含贯通节理岩体能量分配与应力比关系曲线

Figure 4. The ratio of dissipated energy to elastic energy with the ratio of stress to peak stress for layered rock masses

下载: 全尺寸图片幻灯片

图 5 含不同密度断续节理岩体应力应变曲线及能量流

Figure 5. The simulated axial stress and energy variation of jointed rock masses

下载: 全尺寸图片幻灯片

图 6 节理岩体力学参数估算与模拟

Figure 6. The estimated and simulated mechanical parameters of jointed rock mass

下载: 全尺寸图片幻灯片

图 7 耗散能和弹性能之比与应力和峰值应力之比

Figure 7. Ratio of dissipated energy to elastic energy with the ratio of stress to peak stress for jointed rock masses

下载: 全尺寸图片幻灯片

表 1 PFC^3D模型细观参数

Table 1. Mesoscopic parameters of PFC³⁰ rock model

	细观参数	取值
墙体	法向刚度/(N·m^-1)	1.2×10⁹
墙体	切向刚度/(N·m^-1)	1.2×10⁹
颗粒	法向刚度/(N·m^-1)	1.2×10⁸
	切向刚度/(N·m^-1)	1.2×10⁸
	密度/(g·cm^-3)	2 650
	最小粒径/m	1.0×10^-3
	粒径比	3.0
	摩擦系数	0.8
平行粘结模型	抗拉强度/Pa	2.0×10⁸
	内聚力/Pa	5.0×10⁷
	有效弹性模量	1.0×10⁹
	内摩擦角/(°)	30.0
平滑节理模型 (smooth-joint)	法向刚度/(N·m^-1)	1.0×10⁷0.1
	切向刚度(N/m)	1.0×10⁷
	抗拉强度/Pa	2.0×10⁶
	内聚力/Pa	5.0×10⁵
	摩擦系数	0.3
	影响范围	0.1

下载: 导出CSV

表 2 含不同倾角贯通节理岩体的三轴抗压强度

Table 2. Triaxial compressive strengths of layered rock mass with different layer dip angles

节理倾角/ (°)	PFC模拟 TCS(MPa)	σ_c修正系数	H-B估算 TCS/MPa
无	56	1	49.2
15	34	0.61	33.4
30	22	0.39	24.5
45	12	0.21	16.6
60	15	0.27	19.0
75	32	0.57	31.9
90	43	0.77	39.9

下载: 导出CSV

表 3 三组优势节理产状和直径分布参数

Table 3. The distribution parameters of orientations and diameters of dominant joint sets

优势组	产状				直径或迹长
优势组	分布	倾向/(°)	倾角/(°)	k	分布	a	最大/m	最小/m
1	Fisher	120	90	200	power-law	4	2.0	1.2
2		30	20	500		4	2.0	1.2
3		70	45	500		3.2	2.0	1.2

下载: 导出CSV

表 4 断续节理岩体峰值强度和弹性模量估算

Table 4. The estimated TCS and elastic modulus of jointed rock masses

节理密度/ (m²/m³)	J_v (条·m^-3)	GSI	m_b	S	a	σ₁/ MPa	E₀/GPa
节理密度/ (m²/m³)	J_v (条·m^-3)	GSI	m_b	S	a	σ₁/ MPa	PFC^3D	H-B	H-D1	H-D2
0.0	0.0	90	11.89	0.329	0.501	59.8	2.10	97.74	4.47	2.01
0.5	1.59	75	6.96	0.062	0.505	33.2	1.34	39.11	3.47	1.46
2.0	9.87	52	3.06	0.005	0.530	16.7	0.49	10.41	1.73	0.73
4.0	12.57	50	2.85	0.004	0.534	15.8	0.355	9.27	1.54	0.65
6.0	17.98	47	2.56	0.003	0.542	14.4	0.152	7.80	1.27	0.53

下载: 导出CSV

表 5 三轴加载试验含断续节理岩体峰值状态的弹性能估算值

Table 5. The estimated elastic energy in the peak stress of jointed rock mass under the triaxial loading

节理密度/ (m²·m^-3)	弹性能/10⁶J
节理密度/ (m²·m^-3)	PFC^3D	式(9)^*	式(2)
0	6.958	5.470	4.760
0.5	2.901	2.288	2.777
2	0.918	1.121	0.754
4	0.864	1.117	0.742
6	0.450	1.139	0.320
：使用式(9)估算时峰值强度采用H-B准则估算，弹性模量采用H-D准则估算；：使用式(2)估算时峰值强度和弹性模量均使用PFC^3D的模拟结果

下载: 导出CSV

参考文献(24)

[1]	Hoek E, Brown E T.Practical estimates of rock mass strength[J].International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8):1165-1186. doi: 10.1016/S1365-1609(97)80069-X
[2]	Cai M, Kaiser P K, Uno H, et al. Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system[J].International Journal of Rock Mechanics and Mining Sciences, 2004, 41(1):3-19. doi: 10.1016/S1365-1609(03)00025-X
[3]	Marinos V, Marinos P, Hoek E.The geological strength index:Applications and limitations[J].Bulletin of Engineering Geology and the Environment, 2005, 64(1):55-65. doi: 10.1007/s10064-004-0270-5
[4]	Dinc O S, Sonmez H, Tunusluoglu C, et al.A new general empirical approach for the prediction of rock mass strengths of soft to hard rock masses[J].International Journal of Rock Mechanics and Mining Sciences, 2011, 48(4):650-665. doi: 10.1016/j.ijrmms.2011.03.001
[5]	Jiang H.A failure criterion for rocks and concrete based on the Hoek-Brown criterion[J].International Journal of Rock Mechanics and Mining Sciences, 2017, 95:62-72. doi: 10.1016/j.ijrmms.2017.04.003
[6]	周广照, 彭云晖, 许思勇, 等.Hoek-Brown准则在岩石强度各向异性评价中的应用[J].地质科技情报, 2017, 36(2):285-292. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzkjqb201702038
[7]	Cai M, Horii H.A constitutive model of highly jointed rock masses[J].Mechanics of Materials, 1992, 13(3):217-246. doi: 10.1016/0167-6636(92)90004-W
[8]	宋康明, 姜阳厚, 谭志祥, 等.基于随机森林方法的岩石节理粗糙度系数研究[J].地质科技情报, 2018, 37(3):263-267. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzkjqb201803035
[9]	金丰年, 蒋美蓉, 高小玲.基于能量耗散定义损伤变量的方法[J].岩石力学与工程学报, 2004, 23(12):1976-1980. doi: 10.3321/j.issn:1000-6915.2004.12.004
[10]	谢和平, 鞠杨, 黎立云, 等.岩体变形破坏过程的能量机制[J].岩石力学与工程学报, 2008, 27(9):1729-1740. doi: 10.3321/j.issn:1000-6915.2008.09.001
[11]	Song D, Wang E, Li Z, et al.Energy dissipation of coal and rock during damage and failure process based on EMR[J].International Journal of Mining Science and Technology, 2015, 25(5):787-795. doi: 10.1016/j.ijmst.2015.07.014
[12]	黄达, 黄润秋, 张永兴, 等.粗晶大理岩单轴压缩力学特性的静态加载速率效应及能量机制试验研究[J].岩石力学与工程学报, 2012, 31(2):245-255. doi: 10.3969/j.issn.1000-6915.2012.02.003
[13]	温韬, 刘佑荣, 胡政, 等.高应力区砂岩加卸载条件下能量变化规律及损伤分析[J].地质科技情报, 2015, 34(2):200-206. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzkjqb201502029
[14]	朱泽奇, 盛谦, 肖培伟, 等.岩石卸围压破坏过程的能量耗散分析[J].岩石力学与工程学报, 2012, 31(2):245-255. doi: 10.3969/j.issn.1000-6915.2012.02.003
[15]	林杭, 李江腾, 曹平.岩石临界应变能释放率测试及其相关规律[J].中南大学学报:自然科学版, 2013, 44(2):714-717. http://d.old.wanfangdata.com.cn/Periodical/zngydxxb201302040
[16]	Wasantha P L P, Ranjith P G, Shao S S.Energy monitoring and analysis during deformation of bedded-sandstone:Use of acoustic emission[J].Ultrasonics, 2014, 54(1):217-226. doi: 10.1016/j.ultras.2013.06.015
[17]	Potyondy D O, Cundall P A.A bonded-particle model for rock[J].International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8):1329-1364. doi: 10.1016/j.ijrmms.2004.09.011
[18]	Potyondy D O.A flat-jointed bonded-particle material for hard rock[C]//Proceedings of the 46th Rock Mechanics/Geomechanics Symposium, Chicago, IL, American Rock Mechanics Association, 2012
[19]	赵忠虎, 谢和平.岩石变形破坏过程中的能量传递和耗散研究[J].四川大学学报:工程科学版, 2008.40(2):26-31. http://d.old.wanfangdata.com.cn/Periodical/scdxxb-gckx200802005
[20]	Hoek E, Diederichs M S.Empirical estimation of rock mass modulus[J].International Journal of Rock Mechanics and Mining Sciences, 2006, 43(2):203-215. doi: 10.1016/j.ijrmms.2005.06.005
[21]	Bahaaddini M, Sharrock G, Hebblewhite B K.Numerical direct shear tests to model the shear behaviour of rock joints[J].Computers and Geotechnics, 2013, 51(Complete):101-115. https://www.sciencedirect.com/science/article/pii/S0266352X13000293
[22]	Chang C, Zoback M D, Khaksar A.Empirical relations between rock strength and physical properties in sedimentary rocks[J].Journal of Petroleum Science and Engineering, 2006, 51(3/4):223-237. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cdd07ea33a0bb18b7ed228cb59864c8a
[23]	Rajmeny P K, Singh U K, Rathore S S.A new model to estimate rock mass strength accounting for the scale effect[J].International Journal of Rock Mechanics and Mining Sciences, 2004, 41(6):1013-1021. doi: 10.1016/j.ijrmms.2004.03.008
[24]	Schultz R A.Relative scale and the strength and deformability of rock masses[J].Journalof Structural Geology.1996, 18(9):1139-1149. doi: 10.1016/0191-8141(96)00045-4