Susceptibility evaluation of geological disasters in southern Huanggang based on samples and factor optimization
-
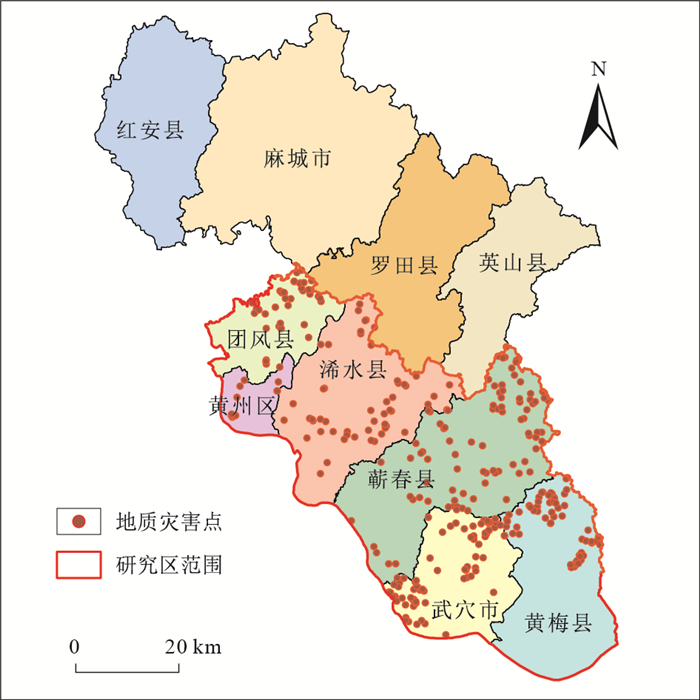
摘要: 为对比信息量模型中灾害数量和灾害面积2种样本的适用性，以黄冈南部地区作为研究对象，探讨了评价因子的优化组合形式，采用信息量模型，根据研究区工程地质条件和地质灾害的特征初选评价因子，结合成功率曲线确定2种样本的因子优化组合，进而通过灾害比率及典型地质灾害点验证易发性评价结果。结果表明：①在单因子评价结果中，2种样本的单因子评价结果的AUC值排列顺序不尽相同，但呈现出一定规律性；②各叠加因子评价结果的准确度均达到因子优化组合的94.9%以上，变化幅度相对较小，且呈现出随因子数量增加而增大的趋势，但并不是越多越好；③2种样本的易发性评价结果都显示出高、较高易发区主要集中于研究区中部及北部地区，低易发区和较低易发区多集中于长江沿岸以及研究区南部，与灾害分布位置相符；④2种样本均为地质灾害易发性评价中信息量模型的有效计算样本，且面积样本的准确度明显优于数量样本。Abstract: Taking southern Huanggang as the study area, this paper contrasted the applicability of the two kinds of calculation samples of the number of disasters and the disaster acreage in the information model, and explored the optimization combination of the evaluation factors. The study established the information model and selected the primary evaluation factors according to the engineering geological conditions and the characteristics of geological disasters of the study area. Also, the paper determined the optimization combination of factors with the success rate curve to verify the susceptibility evaluation results by disaster ratio and typical geological disaster. The results show that: ① In the single factor evaluation results, the order of the two AUC values is different but regular. ② The accuracy of each superposition factor evaluation result is above 94.9% of the optimal combination of factors, and the variation range is relatively small. This shows a trend of increase with the increase of the number of factors, but not as much as possible. ③ The results of the two calculation samples show that the high-prone areas are mainly concentrated in the central and northern parts of the study area, and that the low-prone areas are concentrated along the Yangtze River and in the southern part of the study area, consistent with the location of the disaster. ④ Both are the effective calculation samples of information value model in the geological disaster susceptibility evaluation, and the accuracy of the acreage sample is significantly better than that of the quantity sample.
-
图 1 研究区地理位置及灾害点分布
Figure 1. Location of the study area and distribution of disaster points
图 3 地形地貌因子分级及信息量
a.高程分级及信息量；b.高程因子状态分级图；c.坡度分级及信息量；d.坡度因子状态分级图；e.切割深度分级及信息量；f.切割深度因子状态分级图
Figure 3. Grading and information value of the topography factor
图 4 地质特征因子分级及信息量
a.地层分级及信息量；b.地层因子状态分级图；c.构造分级及信息量；d.构造因子状态分级图
Figure 4. Grading and information value of geological feature factor
图 5 人类工程活动因子分级及信息量
a.公路分级及信息量；b.公路因子状态分级图；c房屋分级及信息量；d.房屋因子状态分级图
Figure 5. Grading and information value of human engineering activity factor
图 6 地表水系因子分级及信息量
a.水系分级及信息量；b.水系因子状态分级图
Figure 6. Grading and information value of surface water system factor
图 7 土地分类因子分级及信息量
a.土地分类分级及信息量；b.土地分类因子状态分级图
Figure 7. Grading and information value of landclassification factor
图 8 面积(a)和数量(b)样本单因子成功率曲线
Figure 8. Success rate curves of single factor of area sample(a), and quantity sample(b)
图 10 面积样品(a)和数量样本(b)易发性评价结果
Figure 10. Evaluation result of susceptibility of area sample (a), and quantity sample (b)
图 11 研究区典型地质灾害平剖面图
Figure 11. Flat section of typical geological disaster in the study area
表 1 AUC值与准确性对照
Table 1. Comparison of AUC value and accuracy
AUC值 0.5 0.5~0.7 0.7~0.9 >0.9 准确性 无 一般 较高 高 
下载: 导出CSV
表 2 单因子成功率曲线对应的AUC值
Table 2. The AUC value of single factor success rate curve
评价因子 切割深度 坡度 构造 地层 高程 公路 土地分类 房屋 水系 面积样本 0.864 0.811 0.801 0.793 0.783 0.748 0.723 0.714 0.709 数量样本 0.695 0.663 0.570 0.638 0.671 0.563 0.628 0.549 0.523 差值 0.169 0.148 0.232 0.156 0.112 0.185 0.096 0.164 0.186
下载: 导出CSV
表 3 叠加因子成功率曲线对应的AUC值
Table 3. The AUC value of superposition factor success rate curve
因子叠加数量/个 面积样本 数量样本 差值 切割深度 0.864 2 0.695 1 0.169 1 2 0.878 4 0.709 4 0.169 0 3 0.905 7 0.714 9 0.190 8 4 0.911 1 0.719 3 0.191 7 5 0.918 9 0.718 4 0.200 4 6 0.922 2 0.721 6 0.200 6 7 0.924 3 0.726 3 0.198 0 8 0.925 3 0.725 5 0.199 8 9 0.922 6 0.726 2 0.196 4
下载: 导出CSV
表 4 研究区2种样本各分级灾害比率
Table 4. Each graded disaster ratio of the two kinds of sample in the study eara
易发等级 灾害密度/% 分级面积比/% 灾害比率 数量 面积 数量 面积 数量 面积 低易发区 1.7 0.1 20.7 19.2 0.084 0.007 较低易发区 7.0 2.4 16.4 21.8 0.425 0.110 中易发区 14.0 5.7 17.8 22.2 0.783 0.255 较高易发区 25.3 7.9 21.2 23.5 1.190 0.334 高易发区 52.0 83.9 23.8 13.3 2.186 6.324
下载: 导出CSV
表 5 浠水县2种样本各分级灾害比率
Table 5. Each graded disaster ratio of the two kinds of sample in Xishui County
易发等级 灾害密度/% 分级面积比/% 灾害比率 数量 面积 数量 面积 数量 面积 低易发区 0.9 0.2 4.5 5.3 0.190 0.041 较低易发区 2.6 3.5 11.9 18.6 0.215 0.191 中易发区 20.5 20.0 27.9 33.0 0.735 0.606 较高易发区 45.3 38.4 35.4 31.1 1.279 1.238 高易发区 30.8 37.8 20.2 12.0 1.522 3.148
下载: 导出CSV
-
[1] 王佳佳, 殷坤龙, 肖莉丽.基于GIS和信息量的滑坡灾害易发性评价:以三峡库区万州区为例[J].岩石力学与工程学报, 2014, 33(4):797-808. https://www.zhangqiaokeyan.com/academic-journal-cn_chinese-journal-rock-mechanics-engineering_thesis/0201254461687.html [2] 杜谦, 范文, 李凯, 等.二元Logistic回归和信息量模型在地质灾害分区中的应用[J].灾害学, 2017, 32(2):220-226. http://www.cnki.com.cn/Article/CJFDTotal-ZHXU201702039.htm [3] 朱吉祥, 张礼中, 周小元, 等.不同区域地质灾害评价方法的组合效应分析[J].地质科技情报, 2012, 31(1):100-105. http://www.cnki.com.cn/Article/CJFDTotal-DZKQ201201018.htm [4] 唐睿旋, 晏鄂川, 唐薇.基于粗糙集和BP神经网络的滑坡易发性评价[J].煤田地质与勘探, 2017, 45(6):129-138. http://www.cnki.com.cn/Article/CJFDTotal-MDKT201706021.htm [5] 高克昌, 崔鹏, 赵纯勇, 等.基于地理信息系统和信息量模型的滑坡危险性评价:以重庆万州为例[J].岩石力学与工程学报, 2006(5):991-996. http://d.wanfangdata.com.cn/periodical/yslxygcxb200605020 [6] 石菊松, 徐瑞春, 石玲, 等.基于RS和GIS技术的清江隔河岩库区滑坡易发性评价与制图[J].地学前缘, 2007, 14(6):119-128. http://www.cnki.com.cn/Article/CJFDTotal-DXQY200706015.htm [7] 冯杭建, 周爱国, 俞剑君, 等.浙西梅雨滑坡易发性评价模型对比[J].地球科学:中国地质大学学报, 2016, 41(3):403-415. http://www.cnki.com.cn/Article/CJFDTotal-DQKX201603006.htm [8] 范强, 巨能攀, 向喜琼, 等.基于结果验证的信息量法地质灾害易发性评价:以贵州省开阳县为例[J].人民长江, 2015, 46(15):65-68. http://www.cnki.com.cn/Article/CJFDTotal-RIVE201515016.htm [9] 戴悦.基于信息量模型的三峡库区滑坡区域危险性评价方法研究[D].北京: 清华大学, 2013. [10] Balamurugan G, Ramesh V, Touthang M.Landslide susceptibility zonation mapping using frequency ratio and fuzzy gamma operator models in part of NH-39, Manipur, India[J].Natural Hazards, 2016, 84(1):1-24. doi: 10.1007/s11069-016-2328-7 [11] Conoscenti C, Maggio C D, Rotigliano E.GIS analysis to assess landslide susceptibility in a fluvial basin of NW Sicily(Italy)[J].Geomorphology, 2008, 94(3/4):325-339. http://cn.bing.com/academic/profile?id=79f514a7c7547b1c61bfcc8d890bf414&encoded=0&v=paper_preview&mkt=zh-cn [12] 刘斌, 殷坤龙, 刘艺梁.基于栅格数据的巴东新城区滑坡空间预测[J].地质科技情报, 2010, 29(3):133-138. http://www.cnki.com.cn/Article/CJFDTotal-DZKQ201003023.htm [13] Pourghasemi H R, Jirandeh A G, Pradhan B, et al.Landslide susceptibility mapping using support vector machine and GIS at the Golestan Province, Iran[J].Journal of Earth System Science, 2013, 122(2):349-369. doi: 10.1007/s12040-013-0282-2 [14] Pradhan B.A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS[J].Computers & Geosciences, 2013, 51(2):350-365. http://cn.bing.com/academic/profile?id=82f21d3f6234e7c61410bbb9db3e3842&encoded=0&v=paper_preview&mkt=zh-cn [15] Bui D T, Pradhan B, Lofman O, et al.Regional prediction of landslide hazard using probability analysis of intense rainfall in the Hoa Binh Province, Vietnam[J].Natrual Hazards, 2013, 66(2):707-730. doi: 10.1007/s11069-012-0510-0 [16] 郑光明.基于信息量法的兰州市幅滑坡灾害易发性评价[D].北京: 中国地质大学(北京), 2017. [17] 李军, 周成虎.基于栅格GIS滑坡风险评价方法中格网大小选取分析[J].遥感学报, 2003, 7(2):86-92. http://www.cnki.com.cn/Article/CJFDTotal-YGXB200302001.htm [18] 阮沈勇, 黄润秋.基于GIS的信息量法模型在地质灾害危险性区划中的应用[J].成都理工学院学报, 2001, 28(1):89-92. http://www.cnki.com.cn/Article/CJFDTotal-CDLG200101017.htm [19] 杨永刚, 殷坤龙, 赵海燕, 等.基于C5.0决策树-快速聚类模型的万州区库岸段乡镇滑坡易滑性区划[J].地质科技情报, 2019, 38(6):189-197. http://www.cnki.com.cn/Article/CJFDTotal-DZKQ201906023.htm [20] 郭天颂, 张菊清, 韩煜, 等.基于粒子群优化支持向量机的延长县滑坡易发性评价[J].地质科技情报, 2019, 38(3):236-243. http://www.cnki.com.cn/Article/CJFDTotal-DZKQ201903025.htm [21] Ilia I, Tsangaratos P.Applying weight of evidence method and sensitivity analysis to produce a landslide susceptibility map[J].Landslides, 2016, 13(2):379-397. doi: 10.1007/s10346-015-0576-3 [22] Hung L Q, Van N T H, Duc D M, et al.Landslide susceptibility mapping by combining the analytical hierarchy process and weighted linear combination methods: A case study in the upper Lo River catchment(Vietnam)[J].Landslides, 2015, 13(5):1285-1301. http://cn.bing.com/academic/profile?id=eac74a331e179fd20bbe044a54e04203&encoded=0&v=paper_preview&mkt=zh-cn [23] 何文秀, 石云.黄土丘陵沟壑区地形复杂度分析[J].测绘科学, 2015, 40(10):146-152. http://www.cnki.com.cn/Article/CJFDTotal-CHKD201510031.htm [24] Basofi A, Fariza A, Ahsan A S, et al.A comparison between natural and Head/tail breaks in LSI(Landslide Susceptibility Index)classification for landslide susceptibility mapping: A case study in Ponorogo, East Java, Indonesia[C]//International Conference on Science in Information Technology.[S.l.]: IEEE, 2016. -
下载:
点击查看大图
计量
- 文章访问数: 712
- PDF下载量: 562
- 被引次数: 0
