Analysis of interaction between lake water and groundwater in beach of Maowusu Lake Basin
-
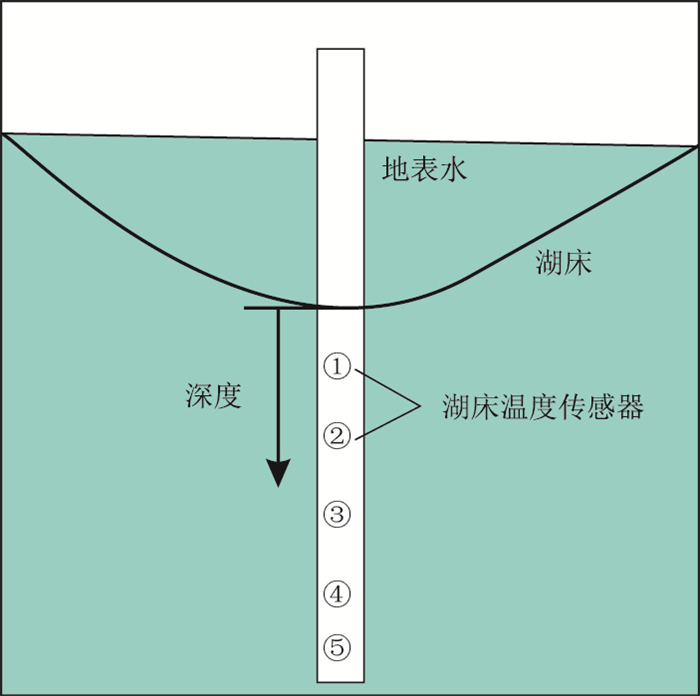
摘要: 湖水与地下水交互作用对于水资源合理开发与利用有着重要意义。基于温度示踪的原理，采用解析法、数值法2种方法，分析了湖床底部埋深0~0.4 m湖水与浅层地下水交互关系，并与水动力学方法进行了对比。结果表明，2018年5月20日至28日，湖水与地下水之间的垂向渗流速度为2×10-7~1×10-6 m/s，且在埋深0.4 m时大于埋深0.2 m处。降水会对解析法的结果造成一定影响，0.4 m处受到降雨影响表现为一定的滞后性。无降雨干扰情况下，数值法与水动力学方法估算结果较为吻合，且3种方法的计算结果处于同一数量级。同时，湖床沉积物体积热容和孔隙度2种参数对计算结果影响较大。在半干旱地区湖水与地下水交互研究中，数据较完备时，数值模拟法是更好的选择。
-
关键词:
- 湖水与地下水交互作用 /
- 温度示踪法 /
- VFLUX2 /
- VS2DH /
- 毛乌素湖盆滩地
Abstract: The interaction between lake water and groundwater is of great significance to the rational development and utilization of water resources. In this paper, based on temperature tracer principle, two methods including of the analytical method and numerical simulation method are used to comprehensively study the interaction between lake water and groundwater with a buried depth of 0-0.4 meters at the lake bed in the beach of Maowusu Lake Basin. In addition, compared with the result by hydrodynamic method. The results show that from May 20 to 28, 2018, the vertical seepage velocity between lake water and groundwater is 2×10-7-1×10-6 m/s, and the seepage velocity at the buried depth is 0.4 m is greater than that at the buried depth of 0.2 m. Precipitation have a certain impact on the results of analytic method, and there is a certain lag in the seepage velocity at the buried depth of 0.4 m. Without less rainfall interference, the results of numerical method and hydrodynamic method are of good agreement, furthermore the results of the three methods are in the same order of magnitude. At the same time, the volume heat capacity and porosity of lake bed sediments have great influence on the results. In the study of interaction between lake water and groundwater in semi-arid areas, numerical simulation is much better choice when the monitoring data are collected completely. -
图 1 湖床温度监测剖面示意图
Figure 1. Schematic diagram of temperature monitoring section of the lake bed
图 3 识别期不同深度模拟温度与实测温度对比
Figure 3. Comparison of simulated temperature and measured temperature at different depths in identification period
图 6 不同湖床深度垂向渗流速度变化
Figure 6. Variation of vertical seepage velocity at different lake bed depths
图 7 数值法(VS2DH)不同月份垂向渗流速度
Figure 7. Vertical seepage velocity in different months by VS2DH numerical method
图 9 湖床深度0.2 m处参数敏感性分析
Figure 9. Sensitivity analysis of 0.2 m lake bed depth parameters
图 10 湖床深度0.4 m处参数敏感性分析
Figure 10. Sensitivity analysis of 0.4 m lake bed depth parameters
图 11 湖床深度0.2 m处参数敏感性分析
Figure 11. Sensitivity analysis of 0.2 m lake bed depth parameters
图 12 湖床深度0.4 m处参数敏感性分析
Figure 12. Sensitivity analysis of 0.4 m lake bed depth parameter
图 13 数值法、解析法与水动力学法垂向渗流速度计算对比
Figure 13. Comparison of numerical method, analytical method and hydrodynamic vertical seepage velocity calculation
表 1 模型识别期的水力学参数
Table 1. Hydraulic parameters model of identification period
参数名 KZZ/ Khh Khh/ (m·s-1) 给水度 孔隙度/% 残余含水率 α/(1· m-1) n 粉砂 1 6.55×10-7 0.1 0.39 0.029 0.057 1.553 细砂 1 5.78×10-6 0.15 0.38 0.029 0.04 8.61 注：Khh为垂向渗透系数；α与进气值有关；n为曲线形状参数 
下载: 导出CSV
表 2 模型识别的热力学参数
Table 2. Thermodynamic parameters of model identification period
参数名 α1 αt Cs/(J·m-3) λmr/(W·m-1·℃-1) λms/(W·m-1·℃-1) Cw/(J·m-3) 粉砂 0.095 0.009 5 2 500 000 0.38 2 4 200 000 细砂 0.095 0.009 5 1 800 000 0.4 1.5 4 200 000 注：λmr为残余含水率下的热通量；λms是饱和含水率下的热通量；Cs为沉积物体积热容；Cw为水体积热容
下载: 导出CSV
表 3 识别期不同深度温度模拟值与实测值误差分析
Table 3. Error snalysis of simulated and measured temperature at different depths in identification period
指标 深度/m 0.15 0.35 0.65 0.85 RE 0.015 5 0.029 9 0.065 9 0.050 8 RMSE/℃ 1.352 8 1.044 9 1.262 9 0.905 1 RE.相对误差；RMSE.均方根误差，下同
下载: 导出CSV
表 4 验证期不同深度温度模拟值与实测值误差分析
Table 4. Error analysis of simulated and measured temperature at different depths in verification period
指标 深度/m 0.15 0.25 0.65 0.85 RE 0.054 6 0.049 1 0.020 1 0.022 2 RMSE/℃ 1.799 3 1.686 2 1.338 5 1.075 6
下载: 导出CSV
-
[1] 余忠波. 地下水水文学原理[M]. 北京: 科学出版社, 2008.Yu Z B. Principles of groundwater hydrology[M]. Beijing: Science Press, 2008(in Chinese). [2] 袁晓芳, 邓娅敏, 杜尧, 等. 江汉平原高砷地下水稳定碳同位素特征及其指示意义[J]. 地质科技通报, 2020, 39(5): 156-163. doi: 10.19509/j.cnki.dzkq.2021.0008Yuan X F, Deng Y M, Du Y, et al. Characteristics of stable carbon isotopes and its implications on arsenic enrichment in shallow groundwater of the Jianghan Plain[J]. Bulletin of Geological Science and Technology, 2020, 39(5): 156-163(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2021.0008 [3] Cartwright K. Tracing shallow groundwater systems by soil temperatures[J]. Water Resources Research, 1974, 10(4): 847-855. doi: 10.1029/WR010i004p00847 [4] Stonestrom D A, Constantz J. Heat as a tool for studying the movement of groundwater near streams[J]. Circular, 2003, 1260: 1-96. [5] Hatch C E, Fisher A T, Revenaugh J S, et al. Quantifying surface water-groundwater interactions using time series analysis of streambed thermal records: Method development[J]. Water Resources Research, 2006, 42(10): 1-14. [6] Stallman R W. Steady one-dimensional fluid flow in a semi-infinite porous medium with sinusoidal surface temperature[J]. Journal of Geophysical Research, 1965, 70(12): 2821-2827. doi: 10.1029/JZ070i012p02821 [7] Goto S, Yamano M, Kinoshita M. Thermal response of sediment with vertical fluid flow to periodic temperature variation at the surface[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B1): 1-11. [8] Keery J, Binley A, Crook N, et al. Temporal and spatial variability of groundwater-surface water fluxes: Development and application of an analytical method using temperature time series[J]. Journal of Hydrology, 2007, 336(1/2): 1-16. [9] Mccallum A M, Andersen M S, Rau G C, et al. A 1-D analytical method for estimating surface water-groundwater interactions and effective thermal diffusivity using temperature time series[J]. Water Resources Research, 2012, 48(11): 1-8. [10] Luce C H, Tonina D, Gariglio F, et al. Solutions for the diurnally forced advection-diffusion equation to estimate bulk fluid velocity and diffusivity in streambeds from temperature time series[J]. Water Resoures, 2013, 49(1): 488-506. doi: 10.1029/2012WR012380 [11] 张佳, 霍艾迪, 赛佳美, 等. 基于温度示踪的渭河西咸新区段潜流交换研究[J]. 人民黄河, 2017, 39(10): 66-69. doi: 10.3969/j.issn.1000-1379.2017.10.014Zhang J, Huo A D, Sai J M, et al. Hyporheic study of Weihe River in Xixian new zone based on temperature tracer[J]. Yellow River, 2017, 39(10): 66-69(in Chinese with English abstract). doi: 10.3969/j.issn.1000-1379.2017.10.014 [12] 葛孟琰, 马瑞, 孙自永, 等. 高寒山区河水与地下水相互作用的温度示踪: 以黑河上游葫芦沟流域为例[J]. 地球科学, 2018, 43(11): 4246-4255. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX201811039.htmGe M Y, Ma R, Sun Z Y, et al. Using heat tracer to estimate river water and groundwater interactions in alpine and cold regions: A case study of Hulugou watershed in upper reach of Heihe River[J]. Earth Science, 2018, 43(11): 4246-4255(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX201811039.htm [13] Kurylyk B L, Irvine D J, Bense V F. Theory, tools, and multidisciplinary applications for tracing groundwater fluxes from temperature profiles[J]. WIREs Water, 2019, 6(1): 1-23. [14] 廖婷, 邢新丽, 石明明, 等. 神农架大九湖PAHs多介质归趋模拟[J]. 地质科技通报, 2020, 39(5): 148-155. doi: 10.19509/j.cnki.dzkq.2020.0512Liao T, Xing X L, Shi M M, et al. Multimedia fate modeling of PAHs in Dajiuhu, Shennongjia[J]. Bulletin of Geological Science and Technology, 2020, 39(5): 148-155(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0512 [15] Gosselin J S, Rivard C, Martel R, et al. Application limits of the interpretation of near-surface temperature time series to assess groundwater recharge[J]. Journal of Hydrology, 2016, 538: 96-108. doi: 10.1016/j.jhydrol.2016.03.055 [16] Lautz L K. Impacts of nonideal field conditions on vertical water velocity estimates from streambed temperature time series[J]. Water Resources Research, 2010, 46(1): 1-14. [17] Roshan H, Rau G C, Andersen M S, et al. Use of heat as tracer to quantify vertical streambed flow in a two dimensional flow field[J]. Water Resources Research, 2012, 48(10): 1-16. [18] Kulongoski J T, Izbicki J A. Simulation of fluid, heat transport to estimate desert stream infiltration[J]. Ground Water, 2008, 46(3): 462-474. doi: 10.1111/j.1745-6584.2007.00403.x [19] Barlow J, Coupe R H. Groundwater and surface-water exchange and resulting nitrate dynamics in the Bogue Phalia Basin in northwestern Mississippi[J]. Journal of Environmental Quality, 2012, 41(1): 155. doi: 10.2134/jeq2011.0087 [20] Russo T A, Fisher A T, Roche J W. Improving riparian wetland conditions based on infiltration and drainage behavior during and after controlled flooding[J]. Journal of Hydrology, 2012, 432/433: 98-111. doi: 10.1016/j.jhydrol.2012.02.022 [21] Ebrahim G Y, Hamonts K, Griensven A, et al. Effect of temporal resolution of water level and temperature inputs on numerical simulation of groundwater-surface water flux exchange in a heavily modified urban river[J]. Hydrological Processes, 2013, 27(11): 1634-1645. doi: 10.1002/hyp.9310 [22] Koch F W, Voytek E B, Day-Lewis F D, et al. 1D TempPro V2: New features for inferring groundwater/surface-water exchange[J]. Groundwater, 2016, 54(3): 434-439. doi: 10.1111/gwat.12369 [23] Su X R, Shu L C, Lu C P. Impact of a low-permeability lens on dune-induced hyporheic exchange[J]. Hydrological Sciences Journal, 2018, 63(5): 818-835. doi: 10.1080/02626667.2018.1453611 [24] Gordon R P, Lautz L K, Briggs M A, et al. Automated calculation of vertical pore-water flux from field temperature time series using the VFLUX method and computer program[J]. Journal of Hydrology, 2012, 420: 142-158. [25] Healy R W, Ronan A D. Documentation of computer program VS2Dh for simulation of energy transport in variably saturated porous media; modification of the US Geological Survey's computer program VS2DT[J]. EP, 1996, 96: 4230. -
下载:
点击查看大图
计量
- 文章访问数: 695
- PDF下载量: 54
- 被引次数: 0
