Identification of Milankovich′s cycle and establishment of astronomical ruler: A case study from the first section of the Sangonghe Formation of Well Mo 21 in Mosuowan area
-
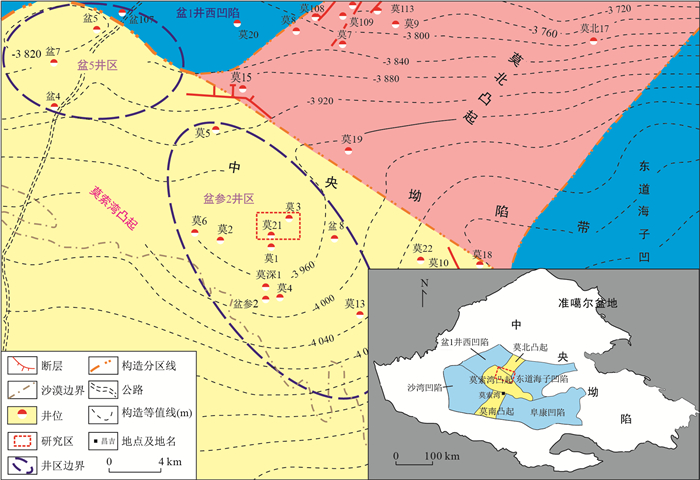
摘要: 依据米兰科维奇理论识别划分旋回，是对传统层序地层学的有力补充，具备高等时约束性，可实现高分辨率旋回识别与高精度等时地层格架的建立。莫索湾地区是准噶尔盆地油气勘探的有利区域之一，其中三工河组一段发育了有效的、成规模的致密气储集层。利用自然伽马测井数据，通过频谱分析等方法，对研究区目标层位进行了米兰科维奇信号识别与旋回划分。以405 ka周期滤波曲线作为基准，借助三工河组底界地质年龄，建立了浮动天文标尺。研究表明，三工河组一段存在米兰科维奇旋回。短期偏心率125 ka周期控制厚度约为29.73 m的旋回；斜率54 ka周期控制厚度约为12.47 m的旋回；岁差24 ka周期控制厚度约为5.62 m的旋回。三工河组一段地质年龄为189.951~190.800 Ma，共识别出了7个短期基准面旋回，由此划分出了7个五级层序，沉积速率从下到上，虽呈现出“减小-增大-持续减小-持续增大”的趋势，但整体变化不大；发育了B1、B2、C1三种类型的短期基准面旋回。Abstract: According to Milankovich′s theory, astronomical forces influence the Earth′s climate change, and the sedimentary process records this change. According to Milankovich′s theory, cycles can be identified and separated, which is a powerful complement to traditional sequence stratigraphy. It has a high-level time and month implementation, which can realize high-resolution periodic identification and the establishment of high-precision isochronous stratigraphic framework. The Mosuowan area is one of the favorable areas for oil and gas exploration in the Junggar Basin. Among them, the first section of the Sangonghe Formation has developed effective and large-scale tight gas reservoirs. Using natural gamma log data, through frequency spectrum analysis and other methods, Milankovich signal identification and period division were performed on the target layer in the study area. Based on the 405 ka periodic filtering curve, a floating astronomical scale based on the geological age at the bottom boundary of the Sangonghe Formation is established.Studies have shown that there is a Milankovich′s cycle in the first section of the Sangonghe Formation. The short-term eccentricity 125 ka period controls the cycle with a thickness of approximately 29.73 m; the slope 54 ka period controls the cycle with a thickness of approximately 12.47 m; the precession 24 ka cycle controls the thickness with a cycle of approximately 5.62 m. The geological age of the first section of the Sangonghe Formation is about 189.951-190.800 Ma. A total of seven short-term base-level cycles have been identified, and seven fifth-order sequences have been divided. "Small-increasing-continuously decreasing-continuously increasing" trend, but the overall change is not large. There are three types of short-term datum cycle: B1, B2, and C1.This article details the Milankovich′s cycle identification process and the establishment of astronomical scales, providing a reference and basis for the high-resolution cycle division of the study area.
-
图 8 自然伽马数据MTM频谱分析图
红线为红燥曲线，蓝线为90%置信度曲线
Figure 8. MTM spectrum analysis of natural gamma data
图 9 自然伽马EHA频谱分析图
白色虚线标注的为短偏心率125 ka周期
Figure 9. EHA spectrum analysis of natural gamma data
图 11 莫21井三工河组一段高分辨率旋回识别与划分
①理论周期滤波曲线中，红色为405 ka周期滤波曲线，蓝色为125 ka周期滤波曲线；②GR偏心率、斜率滤波曲线中的数字代表旋回个数；③GR偏心率、斜率、岁差滤波曲线对应的周期分别为125，54，24 ka
Figure 11. High-frequency cycles identification and division of the Sangonghe Formation in Well Mo 21
表 1 公式(1)中的部分参数[21]
Table 1. Some parameters in formula (1)
k μ′k/(″·a-1) b′k φ′k/(°) 1 3.199 279 0.010 739 170.739 2 13.651 920 0.008 147 109.891 3 10.456 224 0.006 222 -60.044 
下载: 导出CSV
表 2 公式(2)中的部分参数[21]
Table 2. Some parameters in formula (2)
vk/(″·a-1) ak φk/(°) 1 -0.000 001 0.013 774 49 107.581 2 -18.845 166 0.008 703 53 -111.310 3 -5.605 919 0.004 798 13 4.427
下载: 导出CSV
表 3 公式(3)中的部分参数[21]
Table 3. Some parameters in formula (3)
k μk/(″·a-1) bk φk/(°) 1 4.257 564 0.018 986 30.739 2 7.456 665 0.016 354 -157.801 3 17.910 194 0.013 055 140.577
下载: 导出CSV
表 4 轨道理论周期比值
Table 4. Ratio of theoretical orbital period
周期序号 理论天文周期/ka 与P1比值 E1 405 16.88 E2 125 5.21 E3 97 4.04 O1 54 2.25 O2 41 1.71 P1 24 1.00 注：E1，E2，E3为地球的3种偏心率周期；Q1，Q2为地球的2种倾斜度周期；P1为地球的1种岁差周期
下载: 导出CSV
-
[1] Milankovitch M. Kanon der Erdbestrahlung und seine anwendung anf das Eiszeitproblem[M]. Belgrad:Königlich Serbische Akademie, 1941:1-633. [2] 贾东力, 田景春, 林小兵, 等.塔里木盆地顺托果勒地区志留系柯坪塔格组米兰科维奇旋回沉积记录[J].石油与天然气地质, 2018, 39(4):749-758. https://www.cnki.com.cn/Article/CJFDTOTAL-SYYT201804013.htm [3] 吴怀春, 张世红, 冯庆来, 等.旋回地层学理论基础、研究进展和展望[J].地球科学:中国地质大学学报, 2011, 36(3):21-40. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX201103001.htm [4] Weedon G P.Time-series analysis and cyclostratigraphy: Examining stratigraphic records of environmental cycles[M]. Cambridge:Cambridge University Press, 2003. [5] Hinnov L A.New perspectives on orbitally forced stratigraphy[J]. Annual Review of Earth and Planetary Sciences, 2000, 28(1):419-475. doi: 10.1146/annurev.earth.28.1.419 [6] 石巨业, 金之钧, 刘全有, 等.基于米兰科维奇理论的高精度旋回识别与划分:以南图尔盖盆地Ary301井中侏罗统为例[J].沉积学报, 2017, 35(3):436-448. https://www.cnki.com.cn/Article/CJFDTOTAL-CJXB201703002.htm [7] 黄春菊.旋回地层学和天文年代学及其在中生代的研究现状[J].地学前缘, 2014, 21(2):48-66. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY201402006.htm [8] 况军, 姚根顺, 朱国华, 等.准噶尔盆地腹部地区侏罗系三工河组相对优质储集层的成因[J].石油勘探与开发, 2001, 28(6):34-37. doi: 10.3321/j.issn:1000-0747.2001.06.010 [9] 德勒达尔, 张有平, 帕尔哈提, 等.莫索湾地区侏罗系三工河组储集层沉积及成岩作用特征[J].新疆地质, 2003, 21(3):269-273. doi: 10.3969/j.issn.1000-8845.2003.03.002 [10] 吴晓智, 张丛侦, 徐长胜, 等.准噶尔盆地莫索湾凸起侏罗系三工河组沉积特征//佚名.第三届全国沉积学大会[C]. 2004. [11] 张冬玲, 鲍志东, 王建伟, 等.准噶尔盆地中部下侏罗统三工河组二段沉积相及储层特征[J].古地理学报, 2005, 7(2):185-196. doi: 10.3969/j.issn.1671-1505.2005.02.004 [12] 孙靖, 吴爱成, 王然, 等.准噶尔盆地中央坳陷莫索湾地区侏罗系三工河组深层致密砂岩气储集层特征及成因[J].古地理学报, 2017, 19(5):907-918. https://www.cnki.com.cn/Article/CJFDTOTAL-GDLX201705013.htm [13] 高崇龙, 纪友亮, 高志勇, 等.准噶尔盆地腹部深层储层物性保存过程多因素耦合分析[J].沉积学报, 2017, 35(3):577-591. https://www.cnki.com.cn/Article/CJFDTOTAL-CJXB201703015.htm [14] Hinnov L A.Cyclostratigraphy and its revolutionizing applications in the earth and planetary sciences[J]. Bulletin of the Geological Society of America, 2013,125(11/12):1703-1734. http://adsabs.harvard.edu/abs/2013GSAB..125.1703H [15] Hinnov L A, Ogg J G.Cyclostratigraphy and the astronomical time scale[J]. Stratigraphy, 2007, 4(2/3):239-251. http://www.researchgate.net/publication/248529016_Cyclostratigraphy_and_the_Astronomical_Time_Scale [16] 郭少斌, 陈成龙.利用米兰科维奇旋回划分柴达木盆地第四系层序地层[J].地质科技情报, 2007, 26(4):27-30. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ200704005.htm [17] 李斌, 孟自芳, 李相博, 等.靖安油田延长组米兰柯维奇沉积旋回分析[J].地质科技情报, 2005, 24(2):64-70. doi: 10.3969/j.issn.1000-7849.2005.02.012 [18] 李堃宇, 伊海生, 夏国清.基于测井曲线频谱分析柴达木盆地西部七个泉地区上、下油砂山组米兰科维奇旋回特征[J].地质科技情报, 2018, 37(3):87-91. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201803012.htm [19] 刘洋.东海盆地西湖凹陷沉积记录的天文旋回响应[J].地质科技情报, 2020, 39(3):120-128 https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202003016.htm [20] 蒋一鸣.西湖凹陷平湖斜坡带平湖组碎屑锆石U-Pb年龄及米兰科维奇旋回:对源-汇系统及沉积演化的约束[J].地质科技情报, 2019, 38(6):133-140. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201906016.htm [21] Laskar J, Robutel P, Joutel F, et al.A long-term numerical solution for the insolation quantities of the Earth[J]. Astronomy & Astrophysics, 2004,428(1):261-285. http://www.ingentaconnect.com/content/ssam/00046361/2004/00000428/00000001/art00034 [22] 唐凯, 唐正宏, 陶金河, 等.地球运动的长期演化研究进展[J].天文学进展, 2016, 34(2):181-195. https://www.cnki.com.cn/Article/CJFDTOTAL-TWJZ201602003.htm [23] Hinnov L A, Hilgen F J.The geologic time scale: Cyclostratigraphy and astrochronology[M].[S.l.]: Elsevier Science, 2012: 63-83. [24] Prokoph A, Villeneuve M, Agterberg F P, et al.Geochronology and calibration of global Milankovitch cyclicity at the Cenomanian-Turonian boundary[J]. Geology, 2001, 29(6):523-526. doi: 10.1130/0091-7613(2001)029<0523:GACOGM>2.0.CO;2 [25] Schnyder J, Ruffell A, Deconinck J O, et al.Conjunctive use of spectral gamma-ray logs and clay mineralogy in defining Late Jurassic-Early Cretaceous palaeoclimate change (Dorset, U.K.)[J]. Palaeogeography, Palaeoclimatology, Palaeoecology, 2006,299(4):303-320. http://www.sciencedirect.com/science/article/pii/S0031018205003780 [26] Li M, Huang C, Hinnov L, et al.Astrochronology of the Anisian stage (Middle Triassic) at the Guandao reference section, South China[J]. Earth & Planetary Science Letters, 2018,482:591-606. http://www.sciencedirect.com/science/article/pii/S0012821X17306866 [27] Shi J, Jin Z, Liu Q, et al.Terrestrial sedimentary responses to astronomically forced climate changes during the Early Paleogene in the Bohai Bay Basin, eastern China[J]. Palaeogeography, Palaeoclimatology, Palaeoecology, 2018,502:1-12. doi: 10.1016/j.palaeo.2018.01.006 [28] Liu Zhanhong, Huang C, Algeo T J, et al.High-resolution astrochronological record for the Paleocene-Oligocene (66-23 Ma) from the rapidly subsiding Bohai Bay Basin, northeastern China[J]. Palaeogeography, Palaeoclimatology, Palaeoecology, 2018,510:78-92. doi: 10.1016/j.palaeo.2017.10.030 [29] Postma G, Ten Veen J H.Astronomically and tectonically linked variations in gamma-ray intensity in Late Miocene hemipelagic successions of the Eastern Mediterranean Basin[J]. Sedimentary Geology, 1999,128(1/2):1-12. http://www.sciencedirect.com/science/article/pii/S0037073899000548 [30] Vugt N V, Langereis C G, Hilgen F J.Orbital forcing in Pliocene-Pleistocene Mediterranean lacustrine deposits: Dominant expression of eccentricity versus precession[J]. Palaeogeography, Palaeochimatology, Palaeoecology, 2002,172(3/4):193-205. http://www.sciencedirect.com/science/article/pii/S003101820100270X [31] Wonik T.Gammaray measurements in the Kirchrode Ⅰ and Ⅱ boreholes[J]. Palaeogeography, Palaeoclimatology, Palaeoecology, 2001,174(1/3):105. http://www.sciencedirect.com/science/article/pii/S0031018201002887 [32] Ruhl M, Hesselbo S P, Hinnov L, et al.Astronomical constraints on the duration of the Early Jurassic Pliensbachian Stage and global climatic fluctuations[J]. Earth & Planetary Science Letters, 2016,455:149-165. [33] Hüsing S K, Deenen M H L, Koopmans J G, et al.Magnetostratigraphic dating of the proposed Rhaetian GSSP at Steinbergkogel (Upper Triassic, Austria):Implications for the Late Triassic time scale[J]. Earth & Planetary Science Letters, 2011,302:216. http://www.sciencedirect.com/science/article/pii/S0012821X10007648 [34] Renne P R, Deino A L, Hilgen F J, et al.Time scales of critical events around the Cretaceous-Paleogene boundary[J]. Science, 2013,339:684-687. doi: 10.1126/science.1230492 [35] 周路, 张义杰, 雷德文, 等.准噶尔盆地莫索湾凸起构造特征[J].中国石油勘探, 2005, 10(1):16-21. doi: 10.3969/j.issn.1672-7703.2005.01.003 [36] 王剑, 靳军, 向宝力, 等.莫索湾凸起八道湾组储层成岩特征及孔隙演化研究[J].非常规油气, 2015, 2(1):21-27. doi: 10.3969/j.issn.2095-8471.2015.01.004 [37] Yang M, Wang J, Gao Z, et al.Coordinated robust routing by dual cluster heads in layered wireless sensor networks[C]//Anon.8th International symposium on parallel architectures, Algorithms and Networks (ISPAN'05).[S.l.]: IEEE, 2005. [38] 吴雅娟, 高兴, 王辉, 等.改进的小波阈值法在测井曲线去噪中的应用[J].计算机系统应用, 2013, 22(3):182-185. doi: 10.3969/j.issn.1003-3254.2013.03.043 [39] Thomson D J.Spectrum estimation and harmonic analysis[J]. Proceedings of the IEEE, 1982, 70(9):1055-1096. doi: 10.1109/PROC.1982.12433 [40] Meyers R S.Seeing red in cyclic stratigraphy:Spectral noise estimation for astrochronology[J]. Paleoceanography, 2012, 27(3):3228-3240. doi: 10.1029/2012PA002307 [41] Meyers S R, Sageman B B, innov L A.Integrated Quantitative stratigraphy of the Cenomanian-Turonian Bridge Creek Limestone Member using evolutive harmonic analysis and stratigraphic modeling[J]. Journal of Sedimentary Research, 2001, 71(4):628-644. doi: 10.1306/012401710628 [42] Meyers S R, Sageman B B.Quantification of deep-time orbital forcing by average spectral misfit[J]. American Journal of Science, 2007,307(5):773-792. doi: 10.2475/05.2007.01 [43] 杨涵菲.晚白垩世松辽盆地嫩江组米兰科维奇旋回的识别及其古气候响应[D].北京: 中国地质大学(北京), 2017. [44] 石巨业, 金之钧, 刘全有, 等.基于米兰科维奇理论的湖相细粒沉积岩高频层序定量划分[J].石油与天然气地质, 2019, 40(6):1205-1214. https://www.cnki.com.cn/Article/CJFDTOTAL-SYYT201906005.htm [45] Boulila S, Galbrun B, Miller K G, et al.On the origin of Cenozoic and Mesozoic "third-order" eustatic sequences[J]. Earth & Planetary Science Letters, 2011,109(3/4):94-112. http://www.sciencedirect.com/science/article/pii/S0012825211001474 [46] Vail P R.The stratigraphic signatures of tectonics, eustacy and sedimentology: An overview[M]//Anon.Cycles and events in stratigraphy.Berlin: Springer-Verlag, 1991: 617-659. [47] Vail P R, Mitchum J R R M, Thompson Ⅲ S.Seismic stratigraphy and global changes of sea level.Part 3: Relative changes of sea level from coastal onlap[M]// Anon.Seismic Stratigraphy: Applications to hydrocarbon explcration.[S.l.]: American Association of Petroleum Geologists, 1977, 29(22): 63-81. [48] 梅冥相.长周期层序形成机制的探索:层序地层学进展之二[J].古地理学报, 2010, 12(6):711-728. https://www.cnki.com.cn/Article/CJFDTOTAL-GDLX201006010.htm [49] 徐强, 姜烨, 董伟良, 等.中国层序地层研究现状和发展方向[J].沉积学报, 2003, 21(1):155-167. doi: 10.3969/j.issn.1000-0550.2003.01.025 [50] 张坦, 张昌民, 瞿建华, 等.基于米兰科维奇理论的高频沉积旋回识别与对比:以准噶尔盆地玛湖凹陷百口泉组为例[J].东北石油大学学报, 2017, 41(5):54-61. doi: 10.3969/j.issn.2095-4107.2017.05.006 [51] 魏小松, 陆江, 刘蕾, 等.涠西南凹陷流沙港组一段天文旋回识别及高频层序划分[J].中国海上油气, 2018, 30(6):99-108. https://www.cnki.com.cn/Article/CJFDTOTAL-ZHSD201806012.htm [52] 邹卓延, 黄春菊, 李明松, 等.晚渐新世-早中新世气候变化在赤道大西洋的天文响应[J].中国科学:地球科学, 2016, 46(9):1231-1240. https://www.cnki.com.cn/Article/CJFDTOTAL-JDXK201609008.htm [53] 伊海生.地层记录中旋回层序界面的识别方法及原理[J].沉积学报, 2012, 30(6):991-998. https://www.cnki.com.cn/Article/CJFDTOTAL-CJXB201206000.htm [54] 郑荣才, 尹世民, 彭军.基准面旋回结构与叠加样式的沉积动力学分析[J].沉积学报, 2000, 18(3):369-375. doi: 10.3969/j.issn.1000-0550.2000.03.008 -
下载:
点击查看大图
图(11) / 表(4)
计量
- 文章访问数: 851
- PDF下载量: 867
- 被引次数: 0
