Machine learning based on landslide susceptibility assessment with Bayesian optimized the hyperparameters
-
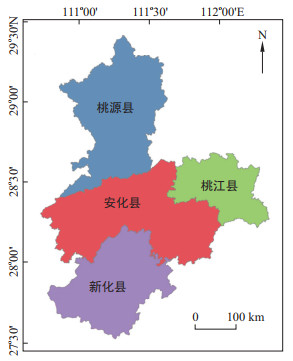
摘要: 利用机器学习模型进行滑坡易发性评价时, 不同的超参数设置往往会导致评价结果的不同。采用贝叶斯算法对4种常见机器学习模型(逻辑回归LR、支持向量机SVM、人工神经网络ANN和随机森林RF)的超参数进行了优化, 探索了该算法对滑坡易发性机器学习模型的优化效果。以湘中地区4县(安化县、新华县、桃江县和桃源县)滑坡易发性评价为例说明该算法的可行性与适用性。基于滑坡历史编录, 确定研究区内1 017个滑坡点, 并选定15个滑坡影响因子, 以此构建滑坡易发性模型的训练集和测试集。利用贝叶斯优化算法对4种机器学习模型的主要超参数进行了优化, 依据优化后的超参数建立了4种优化模型, 并使用AUC值等指标来比较其预测能力。结果表明: 经超参数优化后的4种机器学习模型预测性能均有所提高, 且基于贝叶斯优化的随机森林模型表现最好。Abstract: In machine learning-based landslide susceptibility assessment, there are some differences in the evaluation results obtained by using different hyperparameters. This paper aims to use the Bayesian algorithm to optimize the hyperparameters of four common machine learning models (logistic regression, support vector machine, artificial neural network and random forest) and to explore the optimization effect of this algorithm. Taking the landslide susceptibility assessment of four counties (Anhua, Xinhua, Taojiang, and Taoyuan Counties) in central Hunan as an example, the feasibility and applicability of the algorithm are illustrated. Based on the landslide inventory, 1 017 landslide points in the study area were determined, and 15 landslide influencing factors were selected to construct the training set and test set. The Bayesian optimization algorithm is used to optimize the main hyperparameters of the four machine learning models, and four optimal models are established according to the optimized hyperparameters. The AUC value and other indicators are used to compare the predictive ability of different models. The results show that ① the prediction performance of the hyperparameters optimized models is better than that of the unoptimized models. ② Among the four optimization models, the coupling model of the random forest and Bayesian optimization algorithm has the best prediction performance.
-
Key words:
- landslide /
- susceptibility assessment /
- central Hunan /
- machine learning /
- hyperparameter optimization /
- Bayesian
-
表 1 研究区基于MIC的滑坡影响因子重要性排序
Table 1. Importance ranking of landslide conditioning factors based on MIC
滑坡影响因子 MIC 距道路距离 0.040 距河流距离 0.031 土地利用类型 0.028 高程 0.025 NDVI 0.018 地形湿度指数 0.018 地层岩性 0.017 年汛期降雨量 0.017 微地貌 0.015 坡度 0.013 坡位 0.010 距断层距离 0.008 剖面曲率 0.006 坡向 0.006 平面曲率 0.003 表 2 4种机器学习模型中主要优化的超参数
Table 2. Main optimized hyperparameters in the four machine learning models
模型 超参数 解释 LR solver 损失函数最小化算法包括:sag, Newton CG, lbfgs和liblinear penalty 正则化方法包括:L1和L2 C 正则化系数 SVM kernel 核函数类型包括:linear, poly, rbf, sigmoid和precomputed C 正则化系数 gamma rbf, poly和sigmoid的核函数系数 ANN hidden_layer_sizes 隐藏层层数以及每层的神经元个数 solver 权重求解器包括:lbfgs, sgd和adam alpha L2的正则化系数 RF max_depth 单个决策树的深度 max_features 单个决策树划分时考虑的最大特征数 min_samples_split 分裂一个内部节点(非叶子节点)需要的最小样本数 n_estimators 森林中决策树的个数 表 3 优化前后4种机器学习模型与贝叶斯算法耦合的AUC值比较
Table 3. Comparison of AUC values of the four models before and after optimization by Bayesian
模型类型 LR SVM ANN RF AUC 无超参数优化 0.661 0.701 0.705 0.745 超参数优化 0.708 0.739 0.741 0.771 提升幅度/% 7.1 5.4 5.1 3.5 表 4 超参数优化后的模型性能统计指标
Table 4. Statistical indicators of model performance after hyperparameter optimization
统计指标 LR SVM ANN RF TP 188 188 190 197 TN 192 200 204 221 FP 114 115 105 93 FN 113 104 108 96 敏感度/% 62.46 64.38 63.76 67.24 特异度/% 62.75 63.49 66.02 70.38 准确度/% 62.60 63.92 64.91 68.86 表 5 历史滑坡在各易发性等级的分布情况
Table 5. Distribution of historical landslides in different susceptibility classes
模型 易发性等级 面积/km2 面积占比/% 历史滑坡数 历史滑坡数占比/% 历史滑坡数/面积比值 LR 低 1 212.830 8.05 85 8.36 0.070 1 较低 2 683.407 17.82 68 6.69 0.025 3 中 4 495.363 29.85 239 23.50 0.053 2 较高 4 281.440 28.43 320 31.47 0.074 7 高 2 387.226 15.85 305 29.99 0.127 8 SVM 低 1 909.117 12.68 29 2.85 0.015 2 较低 4 118.570 27.35 150 14.75 0.036 4 中 4 770.588 31.68 309 30.38 0.064 8 较高 2 611.681 17.34 278 27.34 0.106 4 高 1 650.310 10.96 251 24.68 0.152 1 ANN 低 1 777.697 11.80 93 9.14 0.052 3 较低 3 226.806 21.43 104 10.23 0.032 2 中 4 726.266 31.38 281 27.63 0.059 5 较高 3 783.506 25.12 324 31.86 0.085 6 高 1 551.991 10.31 215 21.14 0.138 5 RF 低 3 114.347 20.68 71 6.98 0.022 8 较低 3 761.539 24.98 158 15.54 0.042 0 中 3 198.268 21.24 204 20.06 0.063 8 较高 2 792.637 18.54 258 25.37 0.092 4 高 2 193.475 14.56 326 32.06 0.148 6 -
[1] 黄发明, 殷坤龙, 蒋水华, 等. 基于聚类分析和支持向量机的滑坡易发性评价[J]. 岩石力学与工程学报, 2018, 37(1): 156-167. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201801016.htmHuang F M, Yin K L, Jiang S H, et al. Landslide susceptibility assessment based on clustering analysis and support vector machine[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 156-167(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201801016.htm [2] 程温鸣, 彭令, 牛瑞卿. 基于粗糙集理论的滑坡易发性评价: 以三峡库区秭归县境内为例[J]. 中南大学学报: 自然科学版, 2013, 44(3): 1083-1090. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201303036.htmCheng W M, Peng L, Niu R Q. Landslide susceptibility assessment based on rough set theory: Taking Zigui County territory in Three Gorges Reservoir for example[J]. Journal of Central South University: Science and Technology Edition, 2013, 44(3): 1083-1090(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201303036.htm [3] 黄发明, 陈佳武, 唐志鹏, 等. 不同空间分辨率和训练测试集比例下的滑坡易发性预测不确定性[J]. 岩石力学与工程学报, 2021, 40(6): 1155-1169. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106008.htmHuang F M, Chen J W, Tang Z P, et al. Uncertainties of landslide susceptibility prediction due to different spatial resolutions and different proportions of training and testing datasets[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(6): 1155-1169(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106008.htm [4] Reichenbach P, Rossi M, Malamud B D, et al. A review of statistically-based landslide susceptibility models[J]. Earth Science Reviews, 2018, 180: 60-91. doi: 10.1016/j.earscirev.2018.03.001 [5] Reichenbach P, Galli M, Cardinali M, et al. Geomorphological mapping to assess landslide risk: Concepts, methods and applications in the Umbria region of central Italy[M]. [S.l.]: John Wiley & Sons Ltd., 2004. [6] Galli M, Ardizzone F, Cardinali M, et al. Comparing landslide inventory maps[J]. Geomorphology, 2008, 94(3/4): 289. https://www.sciencedirect.com/science/article/pii/S0169555X07002681 [7] Hansen A, Franks C, Kirk P, et al. Appication of GIS to hazard assessment, with particular reference to landslide in Hong Kong[C]//Carrara A, Guzzeti F. Geographical information system in assessing natural hazards. Dordrecht: The Netherlands, Kluwer Academic Publisher, 1995. [8] 仉义星, 兰恒星, 李郎平, 等. 综合统计模型和物理模型的地质灾害精细评估: 以福建省龙山社区为例[J]. 工程地质学报, 2019, 27(3): 608-622. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201903020.htmZhang Y X, Lan H X, Li L P, et al. Combining statistical model and physical model for refined assessment of geological disaster: A case study of Longshan Community in Fujian Province[J]. Journal of Engineering Geology, 2019, 27(3): 608-622(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201903020.htm [9] 胡燕, 李德营, 孟颂颂, 等. 基于证据权法的巴东县城滑坡灾害易发性评价[J]. 地质科技通报, 2020, 39(3): 187-194. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202003023.htmHu Y, Li D Y, Meng S S, et al. Landslide susceptibility evaluation in Badong County based on weights of evidence method[J]. Bulletin of Geological Science and Technology, 2020, 39(3): 187-194(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202003023.htm [10] Tien-Bui D, Tuan T A, Klempe H, et al. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree[J]. Landslides, 2016, 13(2): 361-378. doi: 10.1007/s10346-015-0557-6 [11] 胡涛, 樊鑫, 王硕, 等. 基于逻辑回归模型和3S技术的思南县滑坡易发性评价[J]. 地质科技通报, 2020, 39(2): 113-121. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202002013.htmHu T, Fan X, Wang S, et al. Landslide susceptibility evaluation of Sinan County using logistics regression model and 3S technology[J]. Bulletin of Geological Science and Technology, 2020, 39(2): 113-121(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202002013.htm [12] 王进, 郭靖, 王卫东, 等. 权重线性组合与逻辑回归模型在滑坡易发性区划中的应用与比较[J]. 中南大学学报: 自然科学版, 2012, 43(5): 1932-1939. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201205051.htmWang J, Guo J, Wang W D, et al. Application and comparison of weighted linear combination model and logistic regression model in landslide susceptibility mapping[J]. Journal of Central South University: Science and Technology Edition, 2012, 43(5): 1932-1939(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201205051.htm [13] 郭天颂, 张菊清, 韩煜, 等. 基于粒子群优化支持向量机的延长县滑坡易发性评价[J]. 地质科技情报, 2019, 38(3): 236-243. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201903025.htmGuo T S, Zhang J Q, Han Y, et al. Evaluation of landslide susceptibility in Yanchang County based on particle swarm optimization-based support vector machine[J]. Geological Science and Technology Information, 2019, 38(3): 236-243(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201903025.htm [14] 钟定清, 王艾伦, 何谦, 等. 交流电力测功机的支持向量机模糊PID控制策略[J]. 中南大学学报: 自然科学版, 2020, 51(3): 661-667. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202003010.htmZhong D Q, Wang A L, He Q, et al. SVR-fuzzy-PID strategy of AC electrical dynamometer[J]. Journal of Central South University: Science and Technology Edition, 2020, 51(3): 661-667(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202003010.htm [15] 吴雨辰, 周晗旭, 车爱兰. 基于粗糙集-神经网络的IBURI地震滑坡易发性研究[J]. 岩石力学与工程学报, 2021, 40(6): 1226-1235. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106013.htmWu Y C, Zhou H X, Che A L. Susceptibility of landslides caused by IBURI earthquake based on rough set-neural network[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(6): 1226-1235(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202106013.htm [16] 刘正洲, 潘伟, 吴爱祥, 等. 硫化矿石常温氧化模拟及基于神经网络的氧化活性预测[J]. 中南大学学报: 自然科学版, 2020, 51(4): 863-871. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202004001.htmLiu Z Z, Pan W, Wu A X, et al. Normal temperature oxidation simulation of sulfide ores and prediction of oxidation activity with neural network[J]. Journal of Central South University: Science and Technology Edition, 2020, 51(4): 863-871(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202004001.htm [17] 张纫兰, 王少军, 李江风. 基于Mamdani FIS模型的滑坡易发性评价研究[J]. 岩土力学, 2014, 35(增刊2): 437-444. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2014S2062.htmZhang R L, Wang S J, Li J F. Research on landslide susceptibility based on Mamdani-FIS model[J]. Rock and Soil Mechanics, 2014, 35(S2): 437-444(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2014S2062.htm [18] 杨永刚, 殷坤龙, 赵海燕, 等. 基于C5.0决策树-快速聚类模型的万州区库岸段乡镇滑坡易发性区划[J]. 地质科技情报, 2019, 38(6): 189-197. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201906023.htmYang Y G, Yin K L, Zhao H Y, et al. Landslide susceptibility evaluation for township units of bank section in Wanzhou district based on C5.0 decision tree and K-means cluster model[J]. Geological Science and Technology Information, 2019, 38(6): 189-197(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201906023.htm [19] 焦江丽, 张雪英, 李凤莲, 等. 同分布强化学习优化多决策树及其在非平衡数据集中的应用[J]. 中南大学学报: 自然科学版, 2019, 50(5): 1112-1118. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201905014.htmJiao J L, Zhang X Y, Li F L, et al. Identically distributed multi-decision tree based on reinforcement learning and its application in imbalanced data sets[J]. Journal of Central South University: Science and Technology Edition, 2019, 50(5): 1112-1118(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201905014.htm [20] 郑迎凯, 陈建国, 王成彬, 等. 确定性系数与随机森林模型在云南芒市滑坡易发性评价中的应用[J]. 地质科技通报, 2020, 39(6): 131-144. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202006015.htmZheng Y K, Chen J G, Wang C B, et al. Application of certainty factor and random forests model in landslide susceptibility evaluation in Mangshi City, Yunnan Province[J]. Bulletin of Geological Science and Technology, 2020, 39(6): 131-144(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202006015.htm [21] Wang B H, Gong N Z. Stealing hyperparameters in machine learning[C]//Anon. 2018 Ieee Symposium on Security and Privacy. New York: IEEE, 2018: 36-52. [22] Aditian A, Kubota T, Shinohara Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia[J]. Geomorphology, 2018, 318: 101-111. doi: 10.1016/j.geomorph.2018.06.006 [23] 徐峰, 范春菊, 徐勋建, 等. 基于变分模态分解和AMPSO-SVM耦合模型的滑坡位移预测[J]. 上海交通大学学报, 2018, 52(10): 1388-1395. https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT201810031.htmXu F, Fan C J, Xun X J, et al. Displacement prediction of landslide based on variational model decomposition and AMPSO-SVM coupling model[J]. Journal of Shanghai Jiaotong University, 2018, 52(10): 1388-1395(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT201810031.htm [24] Ghawi R, Pfeffer J. Efficient hyperparameter tuning with grid search for text categorization using KNN approach with BM25 similarity[J]. Open Comput Science, 2019, 9(1): 160-180. doi: 10.1515/comp-2019-0011 [25] 连志鹏, 徐勇, 付圣, 等. 采用多模型融合方法评价滑坡灾害易发性: 以湖北省五峰县为例[J]. 地质科技通报, 2020, 39(3): 178-186. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202003022.htmLian Z P, Xu Y, Fu S, et al. Landslide susceptibility assessment based on multi-model fusion method: A case study in Wufeng County, Hubei Province[J]. Bulletin of Geological Science and Technology, 2020, 39(3): 178-186(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202003022.htm [26] Weiss A. Topographic position and landforms analysis[C]//Anon. Poster presentation, ESRI user conference. San Diego, CA: [s.n.], 2001: 200. [27] Moore I, Grayson R, Ladson T. Digital terrain modeling: A review of hydrological, geomorphological, and biological applications[J]. Hydrological Processes, 1991, 5: 3-30. doi: 10.1002/hyp.3360050103 [28] 郭子正, 殷坤龙, 黄发明, 等. 基于滑坡分类和加权频率比模型的滑坡易发性评价[J]. 岩石力学与工程学报, 2019, 38(2): 287-300. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201902007.htmGuo Z Z, Yin K L, Huang F M, et al. Evaluation of landslide susceptibility based on landslide classification and weighted frequency ratio model[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(2): 287-300(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201902007.htm [29] Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20(3): 273-297. doi: 10.1007%2FBF00994018.pdf [30] Liu J, Li S L, Chen T. Landslide susceptibility assesment based on optimized random forest model[J]. Geomatics and Information Science of Wuhan University, 2018, 43(7): 1085-1091. https://www.sciencedirect.com/science/article/pii/S0169555X20301732 [31] 吴润泽, 胡旭东, 梅红波, 等. 基于随机森林的滑坡空间易发性评价: 以三峡库区湖北段为例[J]. 地球科学, 2021, 46(1): 321-330. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX202101025.htmWu R Z, Hu X D, Mei H B, et al. Spatial susceptibility assessment of landslides based on random forest: A case study from Hubei section in the Three Gorges Reservoir area[J]. Earth Science, 2021, 46(1): 321-330(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX202101025.htm [32] Snoek J, Larochelle H. Practical bayesian optimization of machine learning algorithms[C]//Anon. Advances in Neural Information Processing Systems 25. Lake Tahoe, Nevada, United States: [s.n.], 2012. [33] Garrido-Merchan E C, Hernandez-Lobato D. Dealing with categorical and integer-valued variables in Bayesian optimization with gaussian processes[J]. Neurocomputing, 2020, 380: 20-35. doi: 10.1016/j.neucom.2019.11.004 [34] Reshef D N, Reshef Y A, Finucane H K, et al. Detecting novel associations in large data sets[J]. Science, 2011, 334: 1518-1524. doi: 10.1126/science.1205438 [35] 黄发明, 叶舟, 姚池, 等. 滑坡易发性预测不确定性: 环境因子不同属性区间划分和不同数据驱动模型的影响[J]. 地球科学, 2020, 45(12): 4535-4549. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX202012017.htmHuang F M, Ye Z, Yao C, et al. Uncertainties of landslide susceptibility prediction: Different attribute interval divisions of environmental factors and different data-based models[J]. Earth Science, 2020, 45(12): 4535-4549(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX202012017.htm [36] Chen W, Baveja A, Melamed B. Temporal shaping of simulated time series with cyclical sample paths[J]. Probability in the Engineering and Information Science, 2018, 32(1): 126-143. doi: 10.1017/S0269964816000401 [37] Youssef A M, Al-Kathery M, Pradhan B. Landslide susceptibility mapping at Al-Hasher area, Jizan (Saudi Arabia) using GIS-based frequency ratio and index of entropy models[J]. Geosciences Journal, 2015, 19(1): 113-134. doi: 10.1007/s12303-014-0032-8 [38] Chen W, Xie X, Peng J, et al. GIS-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method[J]. Catena, 2018, 164: 135-149. doi: 10.1016/j.catena.2018.01.012 [39] Hong H, Ilia I, Tsangaratos P, et al. A hybrid fuzzy weight of evidence method in landslide susceptibility analysis on the Wuyuan area, China[J]. Geomorphology, 2017, 290: 1-16. doi: 10.1016/j.geomorph.2017.04.002 [40] 苏百灵, 刘琳, 谭立云. 湖南省安化县地质灾害调研报告[J]. 科学技术创新, 2019, 33(4): 44-45. doi: 10.3969/j.issn.1673-1328.2019.04.028Su B L, Liu L, Tan L Y. Investigation report on geological hazards in Anhua County, Hunan Province[J]. Scientific and Technological Innovation, 2019, 33(4): 44-45(in Chinese with English abstract). doi: 10.3969/j.issn.1673-1328.2019.04.028 -





 下载:
下载: