Inversion of Rayleigh wave dispersion curves based on antlion optimizer
-
摘要:
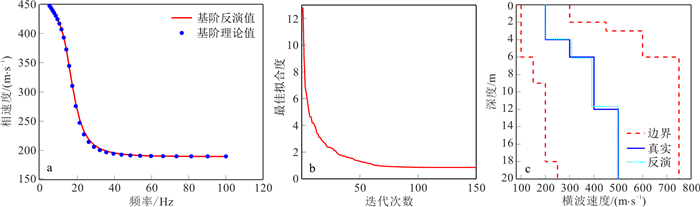
反演瑞雷波频散曲线获得横波速度剖面, 是近地表瑞雷波勘探中最重要的步骤之一; 瑞雷波频散曲线反演是一个多极值、高度非线性问题, 为此引入蚁狮优化算法求解该类问题。蚁狮优化算法是一种群智能算法, 是模仿蚁狮设置陷阱捕食的行为建立的全局优化算法, 该算法收敛速度较快且降低了不同的参数设置对结果产生的影响。通过使用蚁狮优化算法对典型的理论地质模型进行了频散曲线反演, 反演结果表明蚁狮优化算法能够运用在瑞雷波频散曲线反演中且精度较高, 在实测资料中与传统非线性方法进行了对比, 验证了基于蚁狮优化算法频散曲线反演的优势与实用性。
Abstract:Inverting Rayleigh wave dispersion curves to obtain S-wave velocity profiles is one of the most important steps in near-surface Rayleigh wave exploration. Rayleigh wave inversion is a multi-extremum, nonlinear problem, and this paper introduces the antlion optimizer to solve this type of problem. The antlion optimizer is a swarm intelligence algorithm, which is a global optimizer that imitates the behavior of the antlion setting trap predation, which converges faster and reduces the effect of different parameter settings on the result. By using the antlion optimizer to invert the dispersion curve of the typical theoretical geological model, the inversion results show that the antlion optimizer can be applied to the inversion of the dispersion curve with high accuracy, and the advantages and practicality of the dispersion curve inversion based on the antlion optimizer are verified in the measured data compared with the traditional nonlinear methods.
-
Key words:
- Rayleigh wave /
- dispersion curve /
- nonlinear algorithm /
- antlion optimizer
-
图 1 模型1的反演结果
a.基阶反演频散曲线对比图；b.迭代收敛曲线图；c.横波速度剖面对比
Figure 1. Inversion results of Model 1
图 2 模型2的反演结果
a.基阶反演频散曲线对比图；b.迭代收敛曲线图; c.横波速度剖面对比
Figure 2. Inversion results of Model 2
图 3 模型3的反演结果
a.基阶反演频散曲线对比图；b.迭代收敛曲线图; c.横波速度剖面对比
Figure 3. Inversion results of Model 3
图 4 实测资料及其反演
a.实测地震记录；b.实测频散能量图; c.横波速度剖面; d.反演实测对比; e.横波速度迭代曲线; f.层厚度迭代曲线; g.迭代收敛曲线对比; h.实测资料与反演结果对比
Figure 4. Field dataset and inversion results
表 1 模型1参数及反演搜索范围
Table 1. Parameters of Model 1 and search space in the inversion
层号 理论模型 搜索范围 横波速度/(m·s-1) 纵波速度/(m·s-1) 密度/(g·cm-3) 层厚度/m 横波速度/(m·s-1) 层厚度/m 1 200 663 1.9 4 100~300 2~6 2 300 1 149 1.9 2 150~450 1~3 3 400 1 774 1.9 6 200~600 3~9 4 500 2 030 1.9 半空间 250~750 半空间 
下载: 导出CSV
表 2 模型1反演结果统计
Table 2. Statistics of Model 1 inversion results
模型参数 理论值 统计结果 反演结果 相对误差/% 总误差/% Vs1/(m·s-1) 200 200.14 0.07 2.95 Vs2/(m·s-1) 300 307.59 2.53 Vs3/(m·s-1) 400 390.91 2.27 Vs4/(m·s-1) 500 499.31 0.14 H1/m 4 3.96 1.00 H2/m 2 2.15 7.50 H3/m 6 5.57 7.17
下载: 导出CSV
表 3 模型2参数及反演搜索范围
Table 3. Parameters of Model 2 and search space in the inversion
层号 理论模型 搜索范围 横波速度/(m·s-1) 纵波速度/(m·s-1) 密度/(g·cm-3) 层厚度/m 横波速度/(m·s-1) 层厚度/m 1 200 663 1.8 4 100~300 2~6 2 150 497 1.8 2 100~300 1~3 3 300 994 1.8 6 150~450 3~9 4 400 1 326 1.8 半空间 200~600 半空间
下载: 导出CSV
表 4 模型2反演结果统计
Table 4. Statistics of Model 2 inversion results
模型参数 理论值 统计结果 反演结果 相对误差/% 总误差/% Vs1/(m·s-1) 200 200.60 0.30 3.27 Vs2/(m·s-1) 150 147.98 1.34 Vs3/(m·s-1) 300 308.96 2.99 Vs4/(m·s-1) 400 397.25 0.68 H1/m 4 4.20 5.00 H2/m 2 1.93 3.50 H3/m 6 5.50 8.33
下载: 导出CSV
表 5 模型3参数及反演搜索范围
Table 5. Parameters of Model 3 and search space in the inversion
层号 理论模型 搜索范围 横波速度/(m·s-1) 纵波速度/(m·s-1) 密度/(g·cm-3) 层厚度/m 横波速度/(m·s-1) 层厚度/m 1 150 497 1.8 4 50~250 2~6 2 250 829 1.8 2 100~400 1~3 3 200 663 1.8 3 100~400 1.5~4.5 4 400 1 327 1.8 半空间 200~600 半空间
下载: 导出CSV
表 6 模型3反演结果统计
Table 6. Statistics of Model 3 inversion results
模型参数 理论值 统计结果 反演结果 相对误差/% 总误差/% Vs1/(m·s-1) 150 151.33 0.88 3.60 Vs2/(m·s-1) 250 249.31 0.28 Vs3/(m·s-1) 200 217.65 8.82 Vs4/(m·s-1) 400 399.15 0.21 H1/m 4 4.23 5.75 H2/m 2 2.14 7.00 H3/m 3 2.95 1.67
下载: 导出CSV
-
[1] 顾汉明, 宋先海, 刘江平, 等. 用瞬态瑞雷波反演横波速度评价高速公路压碾效果[J]. 地质科技情报, 2001, 20(2): 100-102. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ200102026.htmGu H M, Song X H, Liu J P, et al. Evaluation of the effect of compacting highway surface using shear velocity inversed by instantaneous Rayleigh wave[J]. Geological Science and Technology Information, 2001, 20(2): 100-102(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ200102026.htm [2] 唐韬, 肖晓, 李青. 瞬态瑞雷面波在探测铁路岩溶灾害上的应用[J]. 工程地球物理学报, 2019, 16(3): 339-350. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDQ201903014.htmTang T, Xiao X, Li Q. The application of transient Rayleigh wave to detecting railway karst disaster[J]. Chinese Journal of Engineering Geophysics[J]. 2019, 16(3): 339-350(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-GCDQ201903014.htm [3] 刘威, 朱鸿鹄, 王涛, 等. 基于分布式声波传感的大地探测技术研究进展[J]. 地质科技通报, 2023, 42(1): 29-41. doi: 10.19509/j.cnki.dzkq.2022.0228Liu W, Zhu H H, Wang T, et al. Research progress of earth exploration technologies based on distributed acoustic sensing[J]. Bulletin of Geological Science and Technology, 2023, 42(1): 29-41(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2022.0228 [4] 罗银河, 夏江海, 刘江平, 等. 基阶与高阶瑞利波联合反演研究[J]. 地球物理学报, 2008, 51(1): 242-249. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200801031.htmLuo Y H, Xia J H, Liu J P, et al. Joint inversion of fundamental and higher mode Rayleigh waves[J]. Chinese Journal of Geophysics, 2008, 51(1): 242-249(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200801031.htm [5] 闫英伟, 王者江, 韩飞, 等. 多模式面波非线性反演[J]. 吉林大学学报: 地球科学版, 2019, 49(6): 1768-1779. https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ201906023.htmYan Y W, Wang Z J, Han F, et al. Nonlinear inversion of multi-mode surface waves[J]. Journal of Jilin University: Earth Science Edition, 2019, 49(6): 1768-1779(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ201906023.htm [6] Zhang S X, Chan L S, Chen C Y, et al. Apparent phase velocities and fundamental-mode phase velocities of Rayleigh waves[J]. Soil Dynamics and Earthquake Engineering, 2003, 23(7): 563-569. doi: 10.1016/S0267-7261(03)00069-1 [7] 尹晓菲, 胥鸿睿, 郝晓菡, 等. 水平层状模型中多模式瑞雷波和拉夫波相速度频散曲线的灵敏度分析[J]. 石油地球物理勘探, 2020, 55(1): 136-146. https://www.cnki.com.cn/Article/CJFDTOTAL-SYDQ202001016.htmYin X F, Xu H R, Hao X H, et al. Sensitivity analysis of multi-mode Rayleigh and Love wave phase-velocity dispersion curves in horizontal layered models[J]. Oil Geophysical Prospecting, 2020, 55(1): 136-146(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-SYDQ202001016.htm [8] 于东凯, 宋先海, 江东威, 等. 改进蜂群算法及其在面波频散曲线反演中的应用[J]. 地球物理学报, 2018, 61(4): 1482-1495. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201804022.htmYu D K, Song X H, Jiang D W, et al. Improvement of artificial bee colony and its application in Rayleigh wave inversion[J]. Chinese Journal of Geophysics, 2018, 61(4): 1482-1495(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201804022.htm [9] 宋先海, 张学强, 王一鸣, 等. 近地表弹性介质瑞雷波勘探研究进展与展望[J]. 地质科技通报, 2020, 39(5): 173-182. doi: 10.19509/j.cnki.dzkq.2020.0608Song X H, Zhang X Q, Wang Y M, et al. Recent advances and prospects of near surface elastic Rayleigh waves[J]. Bulletin of Geological Science and Technology, 2020, 39(5): 173-182(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0608 [10] 杨博, 熊章强, 张大洲, 等. 利用自适应混沌遗传粒子群算法反演瑞雷面波频散曲线[J]. 石油地球物理勘探, 2019, 54(6): 1217-1227. https://www.cnki.com.cn/Article/CJFDTOTAL-SYDQ201906006.htmYang B, Xiong Z Q, Zhang D Z, et al. Rayleigh surface-wave dispersion curve inversion based on adaptive chaos genetic particle swarm optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(6): 1217-1227(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-SYDQ201906006.htm [11] 高旭, 于静, 李学良, 等. 自适应权重蜻蜓算法及其在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2021, 56(4): 745-757. https://www.cnki.com.cn/Article/CJFDTOTAL-SYDQ202104009.htmGao X, Yu J, Li X L, et al. Rayleigh wave dispersion curve inversion based on adaptive weight dragonfly algorithm[J]. Oil Geophysical Prospecting, 2021, 56(4): 745-757(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-SYDQ202104009.htm [12] Song X, Tang L, Lv X, et al. Application of particle swarm optimization to interpret Rayleigh wave dispersion curves[J]. Journal of Applied Geophysics, 2012, 84(9): 1-13. [13] Yamanaka H, Ishida H. Application of genetic algorithms to an inversion of surface-wave dispersion data[J]. Bulletin of the Seismological Society of America, 1996, 86(2): 436-444. http://www.researchgate.net/profile/Hiroaki_Yamanaka/publication/265158008_Application_of_Genetic_Algorithms_to_an_Inversion_of_Surface-Wave_Dispersion_Data/links/54487eb70cf2d62c3052a97b [14] Beaty K S, Schmitt D R, Sacchi M, et al. Simulated annealing inversion of multimode Rayleigh wave dispersion curves for geological structure[J]. Geophysical Journal International, 2002, 151(2): 622-631. http://sites.ualberta.ca/~dschmitt/papers/Sim_anneal_gji_2002.pdf [15] Mirjalili S. The ant lion optimizer[J]. Advances in Engineering Software, 2015, 83: 80-98. doi: 10.1016/j.advengsoft.2015.01.010 [16] 侯征, 熊盛青, 杨进, 等. 基于人工蜂群算法的瑞雷波多阶模式非线性联合反演研究[J]. 地球物理学进展, 2018, 33(1): 362-371. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201801049.htmHou Z, Xiong S Q, Yang J, et al. Research on nonlinear joint inversion of multimode Rayleigh wave based on artificial bee colony algorithm[J]. Progress in Geophysics, 2018, 33(1): 362-371(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201801049.htm -
下载:
点击查看大图
计量
- 文章访问数: 547
- PDF下载量: 41
- 被引次数: 0
