Analysis of the spatial variability on a fracture network based on an oriented semivariogram
-
摘要:
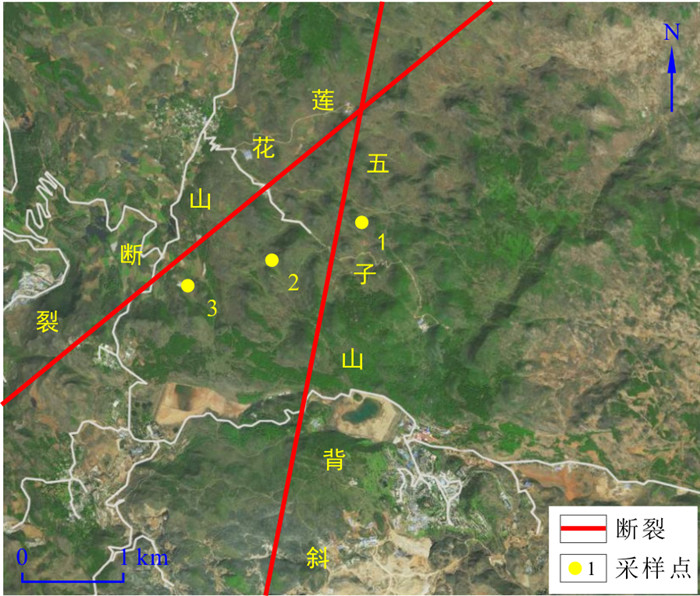
运用地质统计学中的定向半变异函数，研究了个旧高松矿田莲花山断裂和五指山背斜裂隙网络的空间变异性。首先基于ArcGIS将野外露头裂隙网络进行数字化处理并提取裂隙密度和强度，然后依托GSLIB对裂隙密度和强度图沿着0~175°方位角计算，创建了36个实验性半变异函数并进行克里金插值，最后创建归一化的半变异函数图，量化各个断裂强度和断裂密度的二维空间变异性。研究表明，越是靠近断层裂隙密度和强度的空间变化幅度越大，并且其空间变异性存在显著的各向异性。空间变异性最小的方向平行断层且靠近断层，最大方向垂直断层且靠近断层，在褶皱近端空间变异性最小的方向平行于褶皱轴面方向，最大的方向则垂直于褶皱轴面方向。裂隙网络空间变异性质反映了断层和褶皱对裂隙网络发育的不同影响，为构建矿田三维裂隙网络空间分布模型提供参考。
Abstract:Using an oriented semivariogram in geostatistics, this paper studied the spatial variability of the fissure network of Lianhuashan fault and Wuzhishan anticline in Gejiu Gaosong Ore Field. First, the field outcrop fracture network was digitized based on ArcGIS, and the fracture density and intensity were extracted. Then, based on GSLIB, the fracture density and intensity maps were calculated along the azimuth angle of 0-175°, 36 experimental semivariograms were created and Kriging interpolation was carried out, and finally, normalized semivariogram graphs were created to quantify the two-dimensional spatial variability of individual fracture intensity and density. It was indicated that the closer to the fault, the greater the spatial variation of the fracture density and intensity, and the its spatial variability was featured in significant anisotropy. The direction with the smallest spatial variability was parallel and close to the fault, the largest direction was perpendicular and close to the fault, the direction with the smallest spatial variability at the proximal fold was parallel to the axial direction of the fold, and the largest direction was perpendicular to the axial direction of the fold. The spatial variability of the fracture network reflected the different effects of faults and folds on the development of the fracture network and provided a reference for the establishment of a three-dimensional fracture network spatial distribution model in the ore field.
-
Key words:
- geostatistics /
- fracture network /
- spatial variability /
- Gaosong Ore Field /
- Kriging interpolation
-
图 3 裂隙网络轨迹数字化图(n代表相应区域的裂隙或交点数量)
Figure 3. Digitized map of the fracture network trajectory
图 4 创建半变异函数数据点含义图
Figure 4. Schematic diagram of creating a data point for a semivariogram
图 5 创建定向半变异函数变量示意图
Figure 5. Schematic diagram of creating a directional semivariogram variable
表 1 使用Gslib程序时所需输入参数及含义
Table 1. Input parameters and meanings required to use the Gslib program
输入参数 取值 含义 Number of lags 10 每个半方差函数的滞后数 Unit lag separation distance/m 10 每个滞后的间隔距离 Lags tolerance/m 5 滞后容许值 Azimuth/(°) 0, 5…, 175 方位角 Az tol/(°) 10 角度容许值 Bandwidth h/m 20 方位角带宽 Ndir 36 需要考虑的方向数 
下载: 导出CSV
表 2 样本属性
Table 2. Sample attribute
断裂强度 区域1 区域2 区域3 n 503 520 514 x 0.548 3 0.551 6 0.689 6 s 0.234 5 0.242 6 0.258 3 s2 0.054 9 0.058 9 0.066 7 CV 0.427 7 0.439 8 0.374 6 断裂密度 区域1 区域2 区域3 n 663 823 593 x 0.067 7 0.069 5 0.096 5 s 0.087 4 0.089 4 0.098 3 s2 0.007 6 0.007 9 0.009 6 CV 1.290 9 1.286 1 1.018 6 注：s为样本标准偏差; x为样本平均值；CV为变异系数
下载: 导出CSV
表 3 相对变异率
Table 3. Relative variation rate
属性 方位角/(°) 变异体积 相对变异率 区域1 断裂强度 10 103.44 1.28 50 80.62 断裂密度 10 92.93 1.18 50 78.80 区域2 断裂强度 10 93.06 0.82 50 113.52 断裂密度 10 81.26 0.82 50 99.45 区域3 断裂强度 10 83.96 0.77 50 108.51 断裂密度 10 81.17 0.64 50 126.24
下载: 导出CSV
-
[1] Isaaks E H, Srivastava M R. Applied geostatistics[M]. New York: Oxford University Press, 1989. [2] Deutsch C. Geostatistical reservoir modeling[M]. New York: Oxford University Press, 2002. [3] Stein M L. Local variogram models with negative inverse "range" parameters[J]. Spatial Statistics, 2022, 48: 10063. [4] Fouedjio F, Scheidt C, Yang L. A geostatistical implicit modeling framework for uncertainty quantification of 3D geo-domain boundaries: Application to lithological domains from a porphyry copper deposit[J]. Computers and Geosciences, 2021, 157: 104931. doi: 10.1016/j.cageo.2021.104931 [5] Journel D. GSLIB: Geostatistical software library and users guide[M]. New York: Oxford University Press, 1998. [6] Li L, Liu Y H, Liu W, et al. Crack evolution and failure modes of shale containing a pre-existing fissure under compression[J]. ACS Omega, 2021, 6(39): 25461-25475. doi: 10.1021/acsomega.1c03431 [7] Watkins H, Bond C E, Healy D, et al. Appraisal of fracture sampling methods and a new workflow to characterise heterogeneous fracture networks at outcrop[J]. Journal of Structural Geology, 2015, 72: 67-82. doi: 10.1016/j.jsg.2015.02.001 [8] Barbier M, Hamon Y, Callot J P, et al. Sedimentary and diagenetic controls on the multiscale fracturing pattern of a carbonate reservoir: The Madison Formation (Sheep Mountain, Wyoming, USA)[J]. Marine and Petroleum Geology, 2012, 29(1): 50-67. doi: 10.1016/j.marpetgeo.2011.08.009 [9] Mauldon M. Estimating mean fracture trace length and density from observations in convex windows[J]. Rock Mechanics and Rock Engineering, 1998, 31(4): 201-216. doi: 10.1007/s006030050021 [10] Ni A, Qin L X. Performance evaluation of transcriptomics data normalization for survival risk prediction[J]. Briefings in Bioinformatics, 2021, 22(6): bbab257. doi: 10.1093/bib/bbab257 [11] 倪春中, 刘春学, 张世涛, 等. 基于体视学技术的二维数据模拟三维裂隙网络[J]. 石油与天然气地质, 2014, 35(1): 148-152. https://www.cnki.com.cn/Article/CJFDTOTAL-SYYT201401020.htmNi C Z, Liu C X, Zhang S T, et al. 2D data simulation of 3D fracture network based on stereo technology[J]. Oil and Gas Geology, 2014, 35(1): 148-152(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-SYYT201401020.htm [12] 倪春中, 刘春学, 张世涛. 从岩石露头裂隙迹线估算裂隙三维空间方向[J]. 石油与天然气地质, 2013, 34(1): 102-106. https://www.cnki.com.cn/Article/CJFDTOTAL-SYYT201301015.htmNi C Z, Liu C X, Zhang S T, et al. Estimation of three-dimensional spatial orientation of fractures from rock outcrop fracture traces[J]. Oil and Gas Geology, 2013, 34(1): 102-106(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-SYYT201301015.htm [13] 薛佩佩, 文章, 梁杏. 地质统计学在含水层参数空间变异研究中的应用进展与发展趋势[J]. 地质科技通报, 2022, 41(1): 209-222. doi: 10.19509/j.cnki.dzkq.2022.0015Xue P P, Wen Z, Liang X. The application progress and development trend of geostatistics in the study of aquifer parameter spatial variation[J]. Bulletin of Geological Science and Technology, 2022, 41(1): 209-222(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2022.0015 [14] 王恺其, 肖凡. 多点地质统计学的理论、方法、应用及发展现状[J]. 地质科技情报, 2019, 38(6): 256-268. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201906031.htmWang K Q, Xiao F. Theory, method, application and development status of multi-point geostatistics[J]. Geological Science and Technology Information, 2019, 38(6): 256-268(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201906031.htm [15] 陈麒玉, 刘刚, 何珍文, 等. 面向地质大数据的结构-属性一体化三维地质建模技术现状与展望[J]. 地质科技通报, 2020, 39(4): 51-58. doi: 10.19509/j.cnki.dzkq.2020.0407Chen Q Y, Liu G, He Z W, et al. Status and prospect of structure-attribute integrated 3D geological modeling technology for geological big data[J]. Bulletin of Geological Science and Technology, 2020, 39(4): 51-58(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0407 [16] Ilyas A, Kashiwaya K, Koike K. Ni grade distribution in laterite characterized from geostatistics, topography and the paleo-groundwater system in Sorowako, Indonesia[J]. Journal of Geochemical Exploration, 2016, 165: 174-188. [17] Hanke J R, Fischer M P, Pollyea R M. Directional semivariogram analysis to identify and rank controls on the spatial variability of fracture networks[J]. Journal of Structural Geology, 2018, 108: 34-51. [18] 马峰, 曾武林, 陈刚, 等. 地下水封石油洞库深部岩体二维裂隙网络模拟[J]. 地质科技情报, 2011, 30(4): 104-107. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201104017.htmMa F, Zeng W L, Chen G, et al. Two-dimensional fracture network simulation of deep rock mass in underground oil-sealed oil caves[J]. Geological Science and Technology Information, 2011, 30(4): 104-107(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201104017.htm [19] 刘春学, 倪春中, 燕永锋, 等. 利用地质统计学方法模拟岩石裂隙网络的三维空间分布: 以云南个旧高松矿田为例[J]. 地球学报, 2013, 34(3): 347-353. https://www.cnki.com.cn/Article/CJFDTOTAL-DQXB201303013.htmLiu C X, Ni C Z, Yan Y F, et al. Using geostatistical methods to simulate the three-dimensional spatial distribution of rock fissure networks: Taking the Gejiu Gaosong ore field in Yunnan as an example[J]. Chinese Journal of Geosciences, 2013, 34(3): 347-353(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DQXB201303013.htm [20] Liu S F, Wan Z J, Zhang Y, et al. Research on evaluation and control technology of coal pillar stability based on the fracture digitization method[J]. Measurement, 2020, 158: 107713. [21] 蹇龙, 高建国, 亢亢, 等. 云南会泽铅锌矿床1号矿体Pb-Zn元素三维空间变异函数模拟[J]. 地质科技情报, 2015, 34(1): 154-159. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201501024.htmJian L, Gao J G, Kang K, et al. Three-dimensional spatial variation function simulation of Pb-Zn elements in No. 1 ore body of Huize lead-zinc deposit, Yunnan[J]. Geological Science and Technology Information, 2015, 34(1): 154-159(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201501024.htm [22] 周鹏哲, 高锐, 叶卓. 祁连山中部地壳各向异性研究: 来自远震接收函数的证据[J]. 地学前缘, 2022, 29(4): 154-159. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY202204023.htmZhou P Z, Gao R, Ye Z. Crustal anisotropy in the central Qilian Mountains: Evidence from teleseismic receiver functions[J]. Geoscience Frontiers, 2022, 29(4): 154-159(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY202204023.htm [23] 黄兵, 贺方舟, 姜恒. 基于双层规划的普通克里金插值方法研究[J]. 系统工程理论与实践, 2020, 40(5): 1317-1325. https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL202005017.htmHuang B, He F Z, Jiang H. Research on ordinary kriging interpolation method based on two-level programming[J]. Systems Engineering Theory and Practice, 2020, 40(5): 1317-1325(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL202005017.htm [24] Sen Z. Spatial modeling principles in earth sciences[M]. Berlin: Springer International Publishing, 2016. [25] 高歆. 基于线性GSI二维半变异函数各向异性结构建模及估计研究: 以DEM数据为例[J]. 地理研究, 2020, 39(11): 2607-2625. https://www.cnki.com.cn/Article/CJFDTOTAL-DLYJ202011013.htmGao X. Research on anisotropic structure modeling and estimation based on linear GSI two-dimensional semivariogram: Taking DEM data as an example[J]. Geographical Research, 2020, 39(11): 2607-2625(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DLYJ202011013.htm [26] 徐俊龙, 温兴平, 张皓楠, 等. 遥感线性构造中心对称度的尺度效应研究[J]. 地质科技情报, 2019, 38(3): 290-298. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201903032.htmXu J L, Wen X P, Zhang H N, et al. Research on the scale effect of the centrosymmetry of remote sensing linear structures[J]. Geological Science and Technology Information, 2019, 38(3): 290-298(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201903032.htm [27] Hanke J R. Quantifying the spatial variability of fractures and fracture network properties[D]. Dekalb: Northern Illinois University, 2015. [28] Marrett R, Gale J F, Gómez L A, et al. Correlation analysis of fracture arrangement in space[J]. Journal of Structural Geology, 2018, 108: 16-33. [29] 王铭鑫, 范超, 高秉博, 等. 融合半变异函数的空间随机森林插值方法[J]. 中国生态农业学报: 中英文, 2022, 30(3): 451-457. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTN202203010.htmWang M X, Fan C, Gao B B, et al. Spatial random forest interpolation method incorporating semivariograms[J]. Chinese Journal of Ecological Agriculture: Chinese and English, 2022, 30(3): 451-457(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTN202203010.htm [30] 杨阳, 李飒, 孙立强, 等. 半变异函数计算波动范围的方法研究[J]. 武汉大学学报: 工学版, 2021, 54(7): 618-626. https://www.cnki.com.cn/Article/CJFDTOTAL-WSDD202107006.htmYang Y, Li S, Sun L Q, et al. Research on the method of calculating the fluctuation range by semivariogram[J]. Journal of Wuhan University: Engineering Science Edition, 2021, 54(7): 618-626. (in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-WSDD202107006.htm -
下载:
点击查看大图
计量
- 文章访问数: 812
- PDF下载量: 40
- 被引次数: 0
