基于轮廓线层间形态插值的三维地质隐式曲面重构

王权; 邹艳红

doi:10.19509/j.cnki.dzkq.tb20220003

基于轮廓线层间形态插值的三维地质隐式曲面重构

doi: 10.19509/j.cnki.dzkq.tb20220003

王权^{a, b,},
邹艳红^{a, b, ,}

a.
中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083
b.
中南大学地球科学与信息物理学院, 长沙 410083

基金项目:

国家重点研发计划课题 2019YFC1805905

国家自然科学基金项目 41872249

湖南省科技创新计划项目 2021RC4055

详细信息

作者简介:
王权(1997-), 男, 现正攻读地质工程专业硕士学位, 主要从事三维地质建模研究。E-mail: 342008694@qq.com

通讯作者:
邹艳红(1971-), 女, 教授, 主要从事三维地学建模与成矿定量预测研究。E-mail: zouyanhong@csu.edu.cn

中图分类号: P628
计量
- 文章访问数: 673
- PDF下载量: 126
- 被引次数: 0
出版历程
- 收稿日期: 2022-01-04
- 录用日期: 2022-02-22
- 修回日期: 2022-02-21

Three-dimensional geological implicit surface reconstruction based on intermediate contour morphological interpolation

Wang Quan^{a, b
,},
Zou Yanhong^{a, b
, ,}

a.
Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education, Central South University, Changsha 410083, China
b.
School of Geosciences and Info-Physics, Central South University, Changsha 410083, China

摘要

摘要:
地质勘查剖面图上地质体轮廓线分布稀疏, 难以满足复杂地质表面的三维形态重构建模。为此, 提出了一种基于最大相似度匹配轮廓线层间形态插值的三维地质隐式曲面重建方法。该方法首先采用模糊匹配算法, 生成相邻剖面地质体轮廓线顶点映射集; 然后通过计算匹配点相似度获取相似系数, 基于最大相似度匹配原则建立最佳轮廓线顶点映射; 最后基于轮廓线对应顶点计算层间梯度插值作为形态约束, 采用径向基隐式曲面重建方法实现地质体三维曲面重建。通过实例的地质体轮廓线三维隐式建模结果, 验证了该方法不仅可以实现形状大小各异的层间轮廓线形态插值, 同时能够有效克服隐式曲面重建中由于数据稀疏而引起的曲面过度光滑或不连续的现象, 可以为基于隐函数的复杂地质表面重建提供基础。
- 轮廓线层间插值 /
- 相似度匹配 /
- 三维地质建模 /
- 径向基隐式曲面函数 /
- 形态约束
Abstract: Objective
In three-dimensional morphological reconstruction of complex geological surfaces, the sparse geological section data cannot meet the modelling requirements. To overcome it, in this paper, we propose a 3D geological implicit surface reconstruction method based on intermediate contour morphological interpolation at the maximum similarity.
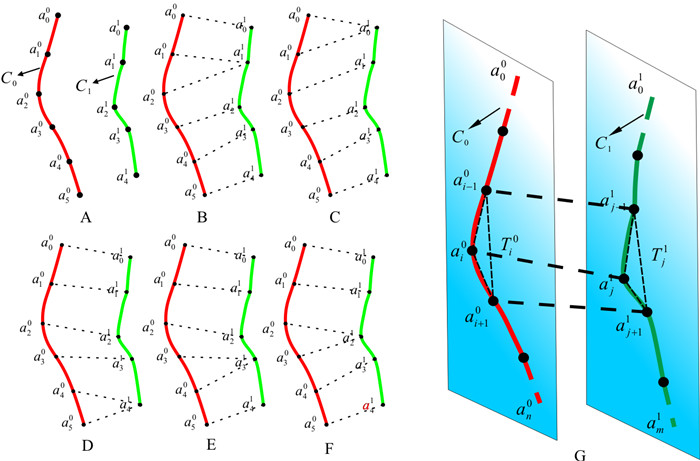
Methods
Firstly, a fuzzy vertex correspondence algorithm was used to generate multiple contour vertex mapping sets of two adjacent contours of the same geological body. Then, the contour similarity coefficient was obtained by calculating the similarity degree of matching points, and the best contour vertex matching map is established based on maximum similarity matching principle; Finally, through intermediate gradient interpolation, the result is used as a morphological constraint to participate in surface reconstruction with radial basis functions (RBFs).
Results
Taking the practical geological section as an example, we constructed the three-dimensional geological implicit model based on morphological interpolation.
Conclusion
Results show that the proposed method can not only realize reasonable intermediate morphology transition between two adjacent sparse contours, but also overcome the phenomenon of excessively smooth or discontinuous surfaces caused by sparse data during implicit surface reconstruction, providing a new basis for complex geological surface reconstruction based on implicit functions.
- intermediate contour interpolation /
- similarity matching /
- three-dimensional geological modeling /
- radial basis functions(RBFs) /
- morphological constraints
注释:

(所有作者声明不存在利益冲突)

HTML全文

图 1 轮廓线之间的特征点匹配方式与相似度计算(图中各物理量的含义见正文)

Figure 1. Vertex correspondence and similarity calculation between two adjacent contours

下载: 全尺寸图片幻灯片

图 2 不闭合轮廓线特征点相似图

A.不闭合轮廓线特征点相似图；B.不闭合轮廓线顶点对应示例；C.示例轮廓线特征图及最佳合法路径

Figure 2. Similarity graph of unclosed contour

下载: 全尺寸图片幻灯片

图 3 闭合轮廓线特征点相似图

A.闭合轮廓线特征点相似图；B.闭合轮廓线顶点对应示例；C.示例轮廓线特征图及最佳合法路径

Figure 3. Similarity graph of closed contour

下载: 全尺寸图片幻灯片

图 4 轮廓线层间梯度插值示意图

Figure 4. Diagram of intermediate contour gradient interpolation

下载: 全尺寸图片幻灯片

图 5 实例地层面轮廓线插值结果以及地层面模型比较图

a.地质剖面示意图; b.地层面轮廓线与梯度插值结果; c.直接基于轮廓线信息隐式构建的地层面模型; d.本方法层间形态插值后隐式构建的地层面模型

Figure 5. Contour interpolation of practical stratum interface and comparison with morphological model

下载: 全尺寸图片幻灯片

图 6 矿体剖面轮廓线插值结果以及矿体模型比较图

a.矿体轮廓线；b.直接基于轮廓线信息隐式构建的矿体模型；c.矿体剖面轮廓线梯度插值结果；d.本方法隐式构建的矿体模型

Figure 6. Contour interpolation of practical ore body and corresponding comparisons

下载: 全尺寸图片幻灯片

参考文献(34)

[1]	Cowan E J, Beatson R K, Ross H J, et al. Practical implicit geological modelling[C]//Anon. Fifth International Mining Geology Conference. Victoria: [s. n. ], 2003: 89-99.
[2]	Calcagno P, Courrioux G, Guillen A, et al. How 3D implicit geometric modelling helps to understand geology: The 3D GeoModeller methodology[C]//Anon. 11th International Congress for Mathematical Geology: Quantitative Geology from Multiple Sources. Belgium: [s. n. ], 2006.
[3]	邹艳红, 何建春. 移动立方体算法的地质体三维空间形态模[J]. 测绘学报, 2012, 41(6): 910-917. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201206022.htm Zou Y H, He J C. A spatial shape simulation method for three-dimensional geological body based on marching cubes algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 910-917(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201206022.htm
[4]	Guo J T, Wu L X, Zhou W H, et al. Section-constrained local geological interface dynamic updating method based on the HRBF surface[J]. Journal of Structural Geology, 2018, 107: 64-72. doi: 10.1016/j.jsg.2017.11.017
[5]	李章林, 吴冲龙, 张夏林, 等. 地质科学大数据背景下的矿体动态建模方法探讨[J]. 地质科技通报, 2020, 39(4): 59-68. doi: 10.19509/j.cnki.dzkq.2020.0408 Li Z L, Wu C L, Zhang X L, et al. Discussion on dynamic orebody modeling with geological science big data[J]. Bulletin of Geological Science and Technology, 2020, 39(4): 59-68(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0408
[6]	陈国旭, 田宜平, 张夏林, 等. 基于勘探剖面的三维地质模型快速构建及不确定性分析[J]. 地质科技情报, 2019, 38(2): 275-280. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201902033.htm Chen G X, Tian Y P, Zhang X L, et al. Rapid construction and uncertainty analysis of 3D geological models based on exploration sections[J]. Geological Science and Technology Information, 2019, 38(2): 275-280(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201902033.htm
[7]	张双腾, 张太怡. 连续断层图象计算机三维重建轮廓点匹配插补算法的研究[J]. 重庆大学学报, 1994, 17(2): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-FIVE402.000.htm Zhang S T, Zhang T Y. Study on computer 3D-reconstruction algorithm of the contour points matching interpolation for serial cross images[J]. Journal of Chongqing University, 1994, 17(2): 1-5(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-FIVE402.000.htm
[8]	杨洋, 潘懋, 吴耕宇, 等. 一种新的轮廓线三维地质表面重建方法[J]. 地球信息科学学报, 2015, 17(3): 253-259. https://www.cnki.com.cn/Article/CJFDTOTAL-DQXX201503002.htm Yang Y, Pan M, Wu G Y, et al. High quality geological surface reconstruction from planar contours[J]. Journal of Geo-information Science, 2015, 17(3): 253-259(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DQXX201503002.htm
[9]	许志勇, 于今, 王世耕. 基于拐点的层间插值算法[J]. 机械工程师, 2008, 8(2): 120-121. https://www.cnki.com.cn/Article/CJFDTOTAL-JXGU200802066.htm Xu Z Y, Yu J, Wang S G. Intermediate interpolation algorithm based on the inflection point[J]. Mechanical Engineer, 2008, 8(2): 120-121(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JXGU200802066.htm
[10]	贾超, 韩志刚, 陈素军. 一种基于关键点的断层轮廓插值方法[J]. 计算机工程与应用, 2007, 43(9): 78-80. https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200709022.htm Jia C, Han Z G, Chen S J. Key points-based interpolation method for slice contour[J]. Computer Engineering and Applications, 2007, 43(9): 78-80(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200709022.htm
[11]	李梅, 毛善君, 马蔼乃. 平行轮廓线三维矿体重建算法[J]. 计算机辅助设计与图形学学报, 2006, 18(7): 1017-1021. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF200607020.htm Li M, Mao S J, Ma A N. Building orebody solid model from planar contours[J]. Journal of Computer-Aided Design & Computer Graphics, 2006, 18(7): 1017-1021(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF200607020.htm
[12]	Kaick O V, Hamarneh G, Zhang H, et al. Contour correspondence via ant colony optimization[C]//Anon. Pacific Conference on Computer Graphics and Applications. Maui: [s. n. ], 2007: 271-280.
[13]	王文成, 李晓伟, 智佳, 等. 基于Hausdorff距离的轮廓线匹配[J]. 西安邮电学院学报, 2007, 12(3): 91-94. https://www.cnki.com.cn/Article/CJFDTOTAL-XAYD200703020.htm Wang W C, Li X W, Zhi J, et al. Contour matching based on Hausdorff distance[J]. Journal of Xi'an University of Posts and Telecommunications, 2007, 12(3): 91-94(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-XAYD200703020.htm
[14]	田宜平, 刘维安, 张夏林. 基于等角度变比例投影的矿体轮廓线自动匹配方法研究[J]. 地质科技通报, 2020, 39(1): 175-180. doi: 10.19509/j.cnki.dzkq.2020.0119 Tian Y P, Liu W A, Zhang X L. Automatic matching of ore body contour line based on equal-angle and variable proportion projection[J]. Bulletin of Geological Science and Technology, 2020, 39(1): 175-180(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0119
[15]	於文雪, 罗立民, 傅瑶, 等. 三维人脑计算机图谱表面重建的层间轮廓线插值[J]. 电子学报, 2000, 28(2): 52-54. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXU200002015.htm Yu W X, Luo L M, Fu Y, et al. Intermediate contour interpolation for computed altas surface reconstruction of 3-D human brain[J]. Acta Electronica Sinica, 2000, 28(2): 52-54(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZXU200002015.htm
[16]	Zhang Y. A fuzzy approach to digital image warping[J]. IEEE Computer Graphics and Applications, 1996, 16(4): 34-41.
[17]	谭国真, 高文. 多边形表示的相似度量[J]. 计算机辅助设计与图形学学报, 1995, 7(2): 96-102. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF502.003.htm Tan G Z, Gao W. Similarity measures for polygons representation[J]. Journal of Computer-Aided Design & Computer Graphics, 1995, 7(2): 96-102(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF502.003.htm
[18]	Lee E T. The shape-oriented dissimilarity of polygons and its application to the classification of chromosome images[J]. Pattern Recognition, 1974, 6(1): 47-60.
[19]	贾建, 康宝生. 分形图形融合算法研究[J]. 纯粹数学与应用数学, 2002, 18(2): 130-134. https://www.cnki.com.cn/Article/CJFDTOTAL-CCSX200202006.htm Jia J, Kang B S. On fractal image blending[J]. Pure and Applied Mathematics, 2002, 18(2): 130-134(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-CCSX200202006.htm
[20]	杨哲, 韩崇昭, 李晨, 等. 基于目标之间拓扑信息的数据关联方法[J]. 系统仿真学报, 2008, 20(9): 2357-2360. https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ200809031.htm Yang Z, Han C Z, Li C, et al. Data association based on target topology[J]. Journal of System Simulation, 2008, 20(9): 2357-2360(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ200809031.htm
[21]	张莹, 蒋大为, 张正贤, 等. 二维迭代函数系统分形吸引子自适应对应变形算法[J]. 计算机辅助设计与图形学学报, 2006, 18(7): 1039-1043. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF200607024.htm Zhang Y, Jiang D W, Zhang Z X, et al. Morphing of two-dimensional IFS fractal attractors with fuzzy correspondence[J]. Journal of Computer-Aided Design & Computer Graphics, 2006, 18(7): 1039-1043(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF200607024.htm
[22]	Lin W C, Liang C C. Dynamic elastic interpolation for 3D medical image reconstruction from serial cross sections[J]. Medical Imaging IEEE Transactions on, 1988, 7(3): 225-232.
[23]	吴松峻. 地形轮廓线三维表面重建算法研究[D]. 武汉: 华中科技大学, 2004. Wu S J. Study on algorithms for reconstructing 3-D surface from terrain contours[D]. Wuhan: Huazhong University of Science & Technology, 2004(in Chinese with English abstract).
[24]	赵增玉, 潘懋, 金毅, 等. 面向钻孔数据的矿体三维形态模拟[J]. 地质科技情报, 2011, 30(2): 122-126. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201102021.htm Zhao Z Y, Pan M, Jin Y, et al. Orebody morphological modeling from boreholes[J]. Geological Science and Technology Information, 2011, 30(2): 122-126(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201102021.htm
[25]	Ohtake Y, Belyaev A, Alexa M, et al. Multi-level partition of unity implicits[J]. ACM Transactions on Graphics, 2003, 22(3): 463-470.
[26]	Kazhdan M, Bolitho M, Hoppe H. Poisson surface reconstruction[C]//Anon. Eurographics Symposium on Geometry Processing. Cagliari: [s. n. ], 2006: 61-70.
[27]	Macedo I, Gois J P, Velho L. Hermite radial basis functions implicits[J]. Computer Graphics Forum, 2011, 30(1): 27-42.
[28]	Guo J T, Wu L X, Zhou W H, et al. Towards automatic and topologically consistent 3D regional geological modeling from boundaries and attitudes[J]. International Journal of Geo-Information, 2016, 5(2): 1-17.
[29]	邹艳红, 李高智, 毛先成, 等. 基于隐函数曲面的三维断层网络建模与不确定性分析[J]. 地质论评, 2020, 66(5): 1349-1360. https://www.cnki.com.cn/Article/CJFDTOTAL-DZLP202005023.htm Zou Y H, Li G Z, Mao X C, et al. Three-dimensional fault-network modeling and uncertainty analysis based on implicit function surface[J]. Geological Review, 2020, 66(5): 1349-1360(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZLP202005023.htm
[30]	Hillier M J, Schetselaar E M, de Kemp E A, et al. Three-dimensional modelling of geological surfaces using generalized interpolation with radial basis functions[J]. Mathematical Geosciences, 2014, 46(8): 931-953.
[31]	Gois J P, Trevisan D F, Batagelo H C. Generalized Hermitian radial basis functions implicits from polygonal mesh constraints[J]. Visual Computer, 2013, 29(6/8): 651-661.
[32]	Zhong D Y, Wang L G, Lin B I, et al. Implicit modeling of complex orebody with constraints of geological rules[J]. Transactions of Nonferrous Metals Society of China, 2019, 29(11): 2392-2399.
[33]	杨鸿翼, 刘亮明, 赵义来. 基于Kriging和Marching cube算法的地学3维形态模拟[J]. 中国图象图形学报, 2008, 13(3): 531-535. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTB200803026.htm Yang H Y, Liu L M, Zhao Y L, et al. 3D geological modelling based on Kriging and Marching cube algorithm[J]. Journal of Image and Graphics, 2008, 13(3): 531-535(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTB200803026.htm
[34]	Wang J, Zhao H, Bi L, et al. Implicit 3D modeling of ore body from geological boreholes data using Hermite radial basis functions[J]. Minerals, 2018, 8(10): 443-457.