A quantitative evaluation method regarding the natural void ratio of undisturbed loess
-
摘要:
天然孔隙比是初始结构的基本表征参数, 故从岩土角度对黄土天然孔隙比分布规律进行分析和预测, 对于掌握原位黄土灾变力学行为并进行灾害预警工作具有重要意义。通过选取典型场地不同层位原状黄土开展了颗粒分析试验、X射线衍射(XRD)试验、天然孔隙比试验和一维固结试验, 分析得到了天然孔隙比与颗粒组分、应力历史的相关规律。结果表明, 天然孔隙比受应力历史和颗粒级配影响, 上覆压力越大, 级配越均匀, 天然孔隙比越小, 同时含水状态也可能是天然孔隙比变化的原因之一。在此基础上, 以层位埋深、颗粒级配不均匀系数和曲率系数、天然含水量作为影响因素, 基于BP神经网络对天然孔隙比进行了定量评价。引入麻雀算法(SSA)与粒子群优化算法(PSO), 建立了BP、SSA-BP与PSO-BP神经网络的天然孔隙比预测模型。随机选取51组实测数据进行了模型训练, 将训练后的模型对16组验证与测试数据进行了预测, 并将预测结果与实测天然孔隙比进行了对比。结果表明基于PSO-BP的神经网络模型预测效果显著优于SSA-BP、BP神经网络模型, 可以有效预测天然孔隙比。
Abstract:Objective The natural void ratio is the most frequently used and important characterisation parameter of the initial structure at the macroscopic level. Therefore, the analysis and prediction of the distribution pattern of the natural void ratio of loess is important for understanding undisturbed loess disaster mechanics behaviour and for disaster early warning from the geotechnical point of view.
Methods In this study, particle analysis tests, XRD tests, natural void ratio tests and 1D consolidation tests were carried out on in situ soil samples from different layers of a typical loess site to analyse the correlation between the natural void ratio and particle fraction and stress history. The results show that the natural void ratio can be affected by the stress history and particle size distribution. The higher the overburden pressure is, the more uniform the grading is and the smaller the natural pore ratio is. The water content may be one of the reasons for the variation in the natural void ratio.
Results On this basis, the burial depth of the layer, the inhomogeneous coefficient and curvature coefficient of particle gradation, and the natural water content are selected as the influencing factors, and the natural void ratio is evaluated quantitatively based on the machine learning algorithm. The SSA and PSO algorithm were introduced to optimise the weights and thresholds of the BP neural network, and natural void ratio predicted models based on the BP, SSA-BP and PSO-BP neural networks were established. The trained BP, SSA-BP and PSO-BP neural network models were then used to predict 16 sets of validation and test data, and the predicted results were compared with the measured natural void ratios.
Conclusion The results show that the PSO-BP-based neural network model predicts significantly better than the SSA-BP and BP neural network models, and can effectively predict the natural void ratio.
-
Key words:
- undisturbed loess /
- natural void ratio /
- particle gradation /
- stress history /
- BP neural network
-
黄土是典型的干旱半干旱沉积物[1]。特定的赋存环境和复杂的形成历史造就了黄土独特的结构特性[2]，即以粉粒为主体骨架的架空结构[3]。在架空结构的控制作用下，典型黄土通常在宏观上表现出欠压实、低重度、低含水量以及垂直节理发育的特征，在微观上大孔隙结构较为明显[4]。冯立等[5]总结了黄土垂直节理微观特征在横纵方向上的发育规律，从不同尺度将微观孔隙展布形态与宏观垂直节理发育现象建立了联系，发现孔隙是黄土灾害发育的优势通道。罗浩等[6]对马兰黄土的变形与孔隙分布特征进行了研究，揭示了大、中架空孔隙在固结过程中的控制作用。实际上，黄土的初始结构作为内在因素，控制了其应力应变关系与灾变模式[7-11]，在给定应力路径条件下，初始结构决定了黄土的一系列力学行为。
土力学中通常利用天然孔隙比来反映黄土初始架空结构特征。从源头上来说，天然孔隙比是黄土地质沉积过程的宏观表现，是刻画黄土初始结构的直接指标。因此，从岩土角度评价天然孔隙比，可为黄土湿陷等灾变力学行为的预测预警提供关键支撑。井彦林[12]采用机器学习方法研究黄土湿陷性问题，提出了天然孔隙比与湿陷性相关性极强。马闫等[13]用数理统计的方法定量给出了湿陷系数与土性指标的关联程度，也提出了天然孔隙比与湿陷系数极为相关，并引入RBF神经网络建立了湿陷系数预测模型。此外，大量研究成果均证明了黄土天然孔隙比与湿陷性存在关联[14-16]。另一方面，Xu等[17-18]和Zuo等[19]的研究表明，黄土对初始结构及应力应变历史具有明显记忆性。在不同应力路径条件下，黄土力学行为显著受到初始孔隙比控制。由此可见，黄土天然孔隙比定量评价对于各类黄土灾变力学行为的预测也具有很大价值。
随着近年来西部大开发以及“一带一路”战略实施，黄土地区开展了大量的工程建设，亟需对黄土灾变结构力学效应进行高效准确的判断，定量预测原状黄土天然孔隙比是实现这一目的的关键切入点，然而目前相关研究仍然较少。笔者拟依托太原地铁1号线典型工程场地获取不同地质层位原状土样，开展室内试验获取天然孔隙比等相关数据，并在此基础上引入机器学习算法，分析天然孔隙比与颗粒组分、物质组成、应力历史、含水条件等因素的相关关系，定量揭示黄土天然孔隙比分布规律并做出预测。
1. 试验土样与方法
1.1 试验土样
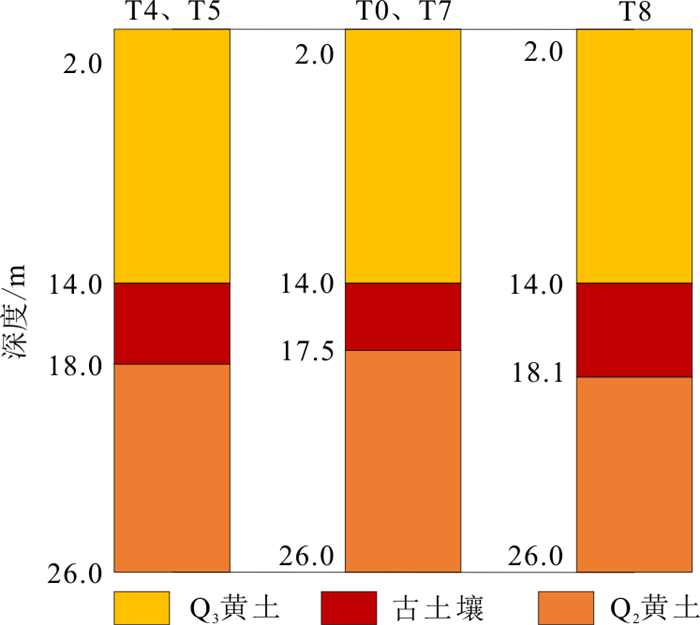
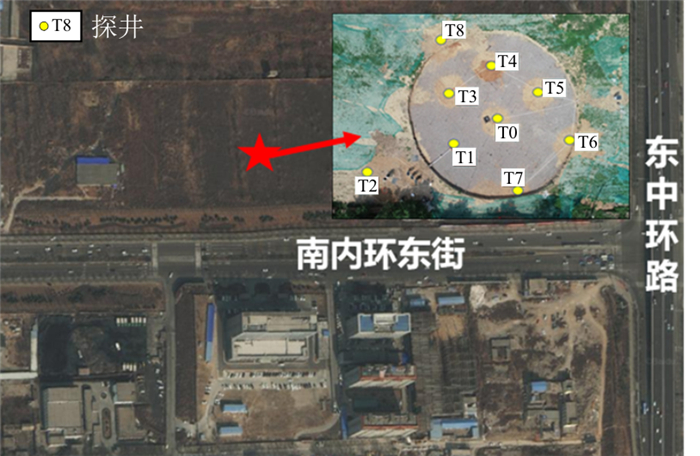
如图 1所示，本研究选取太原东山黄土台塬地区地铁1号线南内环东街站湿陷性黄土场地，试验土样取自T0, T4, T5, T7, T8共5个探井。取样过程中，发现探井T4, T5反映出的地质分层一致，探井T0, T7反映出的地质分层一致，两者之间由于地形起伏而略有差异(图 2)。自距地面2 m深度开始，每隔2 m进行1层取样，最深取样深度26 m。取样时，沿探井内壁按照25 cm×25 cm×15 cm的立方体进行切取，每层取4个试样，计为1组，共取土65组。将试样带回地面后立刻密封处理，尽可能保证运输过程中原状土的含水率不变以及土样不受扰动。
1.2 试验方法
粒径分布是黄土的基本属性之一，对其物理力学性质具有重要影响[20]。本研究利用西安交通大学激光粒度分析仪(LS-909)对探井T0, T5, T8不同深度共39组试样进行了测试，料径测试范围为0.000 2~2.1 mm。该场地黄土类型为粉黄土，最大粒径小于2.1 mm[2, 21]，不超过LS-909的量程。每组试样测试3次，确保误差不超过1%。
考虑到不同沉积年代土层在物质组成上存在细微差异，可能会导致天然孔隙比产生变化，因此选取Q3黄土、古土壤、Q2黄土样品进行X射线衍射试验(XRD)，扫描角度为10°~90°，以查明其物质组成情况。
保证天然孔隙比的测定精度是本研究的关键。根据《土工试验方法标准》(GB/T50123-2019)，在测定天然孔隙比前，首先测定环刀内径与质量。然后拆解现场取回的立方体土样包装，在拆解过程中尽可能避免由人为因素导致试样扰动的现象。接着利用环刀切入立方体土块中，并且在向下按压环刀过程中，采用削土刀切削试样周围土，防止环刀的切入阻力过大导致制样失败。在环刀彻底切入土样后，利用削土刀将环刀试样上下表面切平，原状试样制作完毕。切削下的余土用比重瓶法测定土粒比重，一组5个平行试验，去掉1个最大偏离值，其余4个取平均值作为土粒比重。随后测定原状试样质量以及烘干质量，得到含水率与密度指标，最终换算得到天然孔隙比。对于同一探井同一深度，至少进行一组3个平行样品测试，保证误差在1%以内，取平均值作为代表值。
对于同一沉积年代的土层，为探究应力历史对天然孔隙比的影响，试验仪器采用单杠杆固结仪，以一维固结试验模拟沉积应力。选取相对浅层土样进行加载，获取孔隙比随应力变化情况。对于Q3黄土，考虑到井深2 m处的试样容易受到地面工程扰动，井深4 m处的试样扰动概率较低且上覆荷载较低，故选取井深4 m处的试样进行加载；对于古土壤层，选择井深16 m处的试样进行加载；对于Q2黄土，选择井深22 m处的试样进行加载。具体加载方式见表 1。
表 1 一维固结试验方案Table 1. One-dimensional consolidation test scheme土层类型 固结压力/kPa Q3黄土 14.35, 64.40, 120.45, 222 古土壤 259, 333 Q2黄土 370, 480 5个探井的对应深度均进行一维固结试验，每个深度一组做3个平行试验，控制固结过程中千分表读数误差在2%以内，取千分表读数的平均值进行换算得到加载过程中的孔隙比。
2. 试验结果与分析
2.1 颗粒分布试验
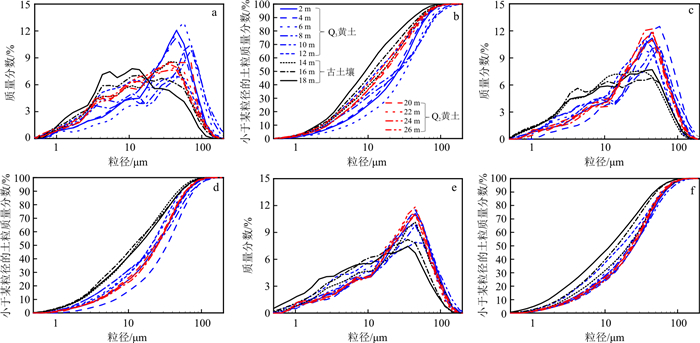
颗粒分布试验结果见图 3。对于T0探井，井深2~14 m的Q3黄土粒径分布整体差异不大，但其中井深2~8 m处试样粒径分布表现更一致，基本呈现单峰分布，8~12 m粒径分布的峰值含量相比更低且峰值粒径更大，并且逐步出现双峰分布，12~14 m粒径分布表现为双峰。对于T5和T8探井，2~14 m的Q3黄土与18~26 m的Q2黄土粒径分布曲线差距不大，基本表现为单峰型分布特征，个别深度(T5探井8，10 m)有双峰趋势。整体而言，40~50 μm范围内粒径含量最高，其微分含量大于10%。14~18 m的古土壤层粒径分布曲线在0~3 μm和大于60 μm范围内与Q3、Q2黄土的粒径分布近似一致，但古土壤在在3~50 μm范围内粒径分布密度更为均匀，特别是3~20 μm的颗粒含量相较黄土有显著增加，且随着深度的增大，细小颗粒含量有增大的趋势。可以看到，粒径分布曲线的差异与沉积地层划分具有一致性，从颗粒分布的角度上可以将Q3黄土、Q2黄土划分为一类，古土壤层划分为一类。
图 3 粒径级配曲线a.T0探井粒径微分质量分数曲线; b.T0探井累计质量分数曲线; c.T5探井粒径微分质量分数曲线; d. T5探井累计质量分数曲线; e.T8探井粒径微分质量分数曲线; f.T8探井累计质量分数曲线Figure 3. Particle size distribution curves2.2 XRD试验
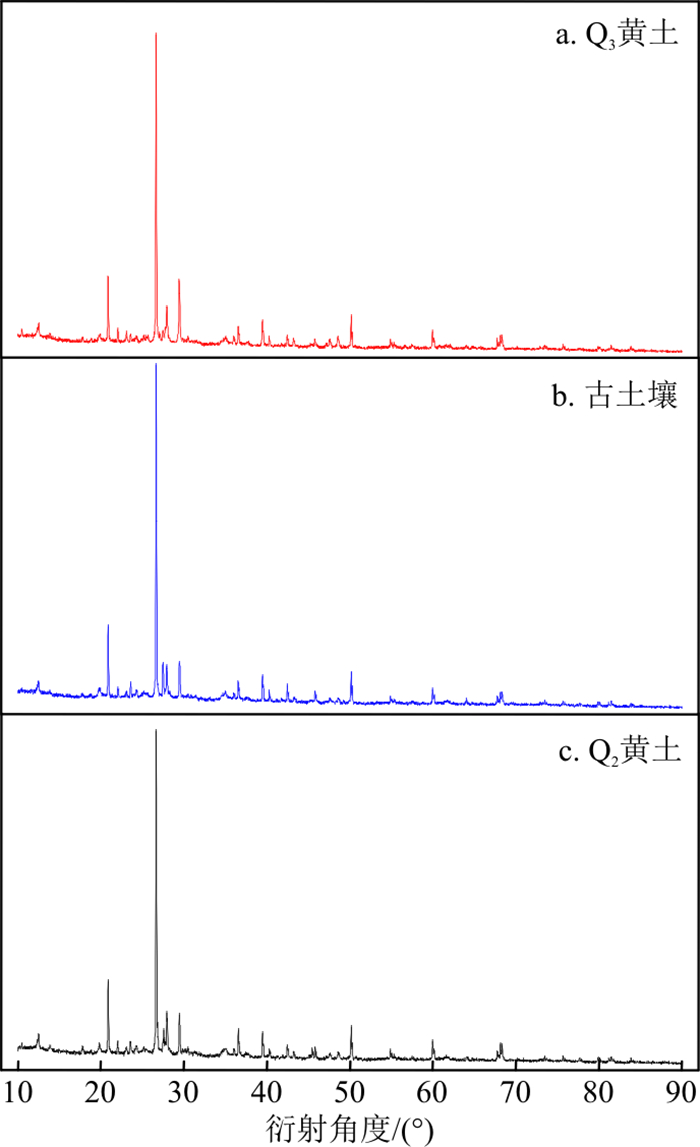
X射线衍射(XRD)试验结果如图 4所示。可得Q3黄土、古土壤、Q2黄土衍射角基本一致，表明试验场地内不同沉积年代黄土的物质组成一致。从地质成因方面而言，黄土源区包括青藏高原东北缘的祁连山、蒙古西部的戈壁-阿尔泰(Gobi-Altai)山脉以及蒙古南部的杭爱(Hangayn)山脉[22-23]。来自祁连山的黄土物源被黑河、石羊河、黄河以及其他主要由冰川融水补给的地表径流带到了腾格里沙漠、巴丹吉林沙漠以及毛乌素沙漠的边缘，来自戈壁-阿尔泰和杭爱山脉的黄土物源被降水引起的短期洪水带到了巴丹吉林沙漠北部[22-24]。在冬春季，受蒙古-西伯利亚高压系统影响，蒙古气旋产生的亚洲季风是黄土高原黄土形成的主要原因[23-24]。受到风成影响，黄土物质组分具有高度一致性[25]。因此，可以排除研究场地内天然孔隙比受到物质组成的影响。
图 4 Q3黄土(a)、古土壤(b)以及Q2黄土(c)的XRD曲线Figure 4. XRD curves of Q3 loess(a), paleosols (b) and Q2 loess (c)2.3 天然孔隙比测定与一维固结试验
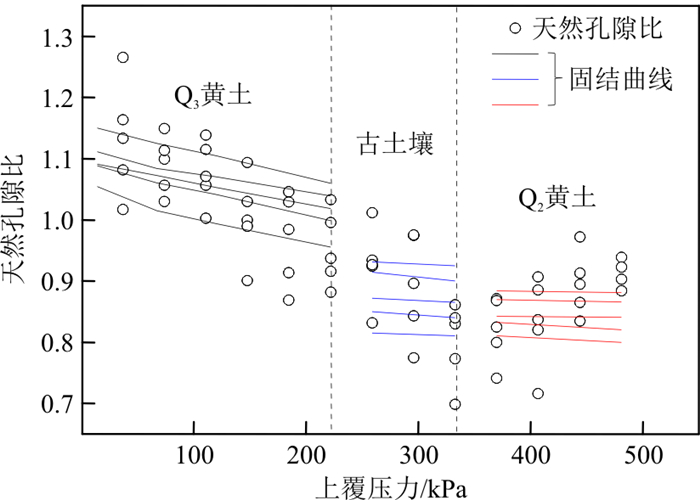
天然孔隙比的测试结果如图 5中空心圆点所示，按照土体密度，将不同深度换算为上覆压力。由图 5可以看出，对于同一深度，5个不同探井测得的孔隙并不相同，而是在一个范围内分布，这表现出了天然孔隙比均在场地尺度下的不确定性。然而从场地整体地层的角度，天然孔隙比的变化仍呈现出一定的规律。对于Q3黄土层和古土壤层，天然孔隙比随深度(应力)增大呈逐渐减小趋势；对于Q2黄土层，天然孔隙比随深度(应力)增大呈平缓甚至逐渐增大趋势。
图 5 天然孔隙比与Q3黄土、古土壤和Q2黄土的固结曲线Figure 5. Natural void ratio and consolidation curves of Q3 loess, paleosols and Q2 loess为了进一步明确应力历史对天然孔隙比的影响，将原位沉积与模拟加载2种应力历史条件下天然孔隙比的变化情况进行了对比。图 5中将各探井4, 16, 22 m土层样品的固结曲线与实测天然孔隙比进行了同时展示。
从Q3黄土的固结曲线与天然孔隙比关系(图 5)来看，在上覆压力为10~150 kPa时，天然孔隙比基本位于各条固结曲线上，变化趋势与固结变形一致；在上覆压力为180~220 kPa时，天然孔隙比低于固结曲线，表现出更明显的减小趋势。结果表明，Q3黄土天然孔隙比受应力历史主导，上覆荷载越大，天然孔隙比越小。值得注意的是，上覆压力180~220 kPa所对应的10~12 m深度土层，其天然含水量为12%~18%，而4 m深度土层的天然含水量约为10%。由于含水量越大，黄土初始孔隙结构破坏程度越高，黄土的天然孔隙比越小。因此不同深度土层天然含水量的差别可能是造成天然孔隙比随上覆压力增大而快速减小的原因。
从古土壤的固结曲线与天然孔隙比关系(图 5)来看，天然孔隙比随深度减小的趋势比固结曲线变化趋势更为显著。同时注意到14~18 m深度土层含水量维持在15%~18%范围内，表明此阶段应力历史与含水状态不是天然孔隙比变化的控制因素。从图 3可以发现古土壤层的粒径分布与黄土层不一致，细颗粒含量较高，而且随着深度增大细颗粒含量进一步增加，孔隙更容易被充填，宏观上形成较小孔隙比。因此对于古土壤层，控制天然孔隙比的主要影响因素为颗粒级配。
从Q2黄土固结曲线与天然孔隙比关系(图 5)来看，天然孔隙比变化趋势平缓乃至略微增大，固结曲线近似平行，表明此阶段应力历史不是天然孔隙比变化的控制因素。同时Q2黄土的粒径分布与Q3黄土的粒径分布近似，且随深度增加差别不大(图 3)，因此粒径分布也不是控制Q2黄土天然孔隙比发生变化的主要因素。注意到对于20~26 m深度黄土层，天然含水量范围随着深度增大从16%~18%减小到12%~13%，因此天然含水量的差异可能使得浅层Q2黄土初始孔隙结构受到破坏作用更强，孔隙比更小。
综上所述，由于地层情况不同，天然孔隙比在各个地层下受到的主要影响因素也不同，但可以发现，天然孔隙比受应力历史、粒径分布控制，含水状态也有可能是天然孔隙比变化的影响因素之一。
2.4 天然孔隙比影响因素分析
2.4.1 土层埋深
应力历史是天然孔隙比主要影响因子，而埋深是反映应力历史的重要指标[26-27]。根据实测天然孔隙比数据，当其他因素一定时，土层埋深与天然孔隙比近似成反比线性关系，而且固结试验结果表明，在低应力水平下，天然孔隙比与埋深的反比关系更为明显。随着应力水平的升高，天然孔隙比减小趋势逐渐变缓。
2.4.2 不均匀系数和曲率系数
根据试验结果，颗粒级配也是天然孔隙比的又一重要影响因子[28-30]。不均匀系数反映出级配曲线的陡缓情况。当其他情况一致时，不均匀系数越大，土颗粒的分散性越好，越容易形成较小的天然孔隙比。土的粒径级配曲线的另一重要指标是曲率系数, 可反映出级配曲线的连续性情况。为反映颗粒级配对天然孔隙比的控制作用，将不均匀系数与曲率系数均考虑为影响因素。
2.4.3 天然含水量
根据固结试验结果，Q2黄土的天然孔隙比与固结曲线所对应的孔隙比不同，且天然孔隙比出现上扬趋势。在粒径曲线、应力历史一致的情况下，水力历史的不同可能造成了孔隙比的异常变化。
如图 6所示，从场地整体地层的角度，天然孔隙比随天然含水量的增大而减小，因此将天然含水量作为天然孔隙比的影响因素是必要的[31-33]。
图 6 天然孔隙比随天然含水量变化散点图Figure 6. Scatter plot of the natural void ratio versus water content2.4.4 天然孔隙比定量评价方法
传统的数据分析方法，往往通过选取特定一维变量函数形式来描述2类指标之间的相关关系，在适用性和精确性上均有较大局限。通过上述分析可以看到，对于黄土天然孔隙比而言，其大小受多种因素影响，指标间存在多维相关关系，并且数据之间数学关系复杂，难以用特定的一维函数形式进行拟合。而机器学习中的BP(back propagation)神经网络算法具备自学习、自适应以及较强的非线性映射能力和泛化能力，能够对试验数据展开有效挖掘从而建立起多维变量之间的相关关系[34]。对于本项研究而言，通过BP神经网络算法的应用，则能反映出天然孔隙比受各个因素的共同影响情况。与此同时，考虑到BP神经网络存在的收敛速度较慢以及容易陷入局部最小的问题，本研究结合麻雀搜索算法(sparrow search algorithm, 简称SSA)以及粒子群算法(particle swarm optimization, 简称PSO)对BP神经网络的寻优能力进行优化，以期提高天然孔隙比定量评价的精度。
3. 基于神经网络的天然孔隙比预测
3.1 神经网络
3.1.1 BP神经网络
BP神经网络是误差反向传播的多层前馈网络。网络拓扑结构由输入层、隐含层以及输出层组成。其中单隐含层组成的前向3层神经网络可以实现自定义精度逼近非连续函数。故本研究采用单隐含层的BP神经网络。
3.1.2 基于SSA优化的BP神经网络
麻雀搜索算法[35]将麻雀觅食行为分为3类：①作为发现者去找寻食物；②作为加入者跟随发现者觅食；③作为侦察者决定是否放弃食物。
在SSA中，若确定麻雀数量n，最大迭代次数M，变量维数d，则每个麻雀的位置对应一个解。
发现者搜索范围最广，其位置更新公式如下：
xt+1ij={xtij⋅exp(−iα⋅M),R2<STxtij+QL,R2⩾ST (1) 式中: t为当前迭代数; xij为第i个麻雀在第j维的位置；α∈rand(0, 1];Q为服从正态分布的随机数; L为1×d的矩阵; R2为预警值; ST为安全值。
加入者跟随发现者进行觅食，以获取更高的适应度。位置更新公式如下：
xt+1ij={Q⋅exp(xtuj−xtiji2),i>n2xt+1pj+|xtij−xt+1pj|A+L, 其他 (2) 式中: xpj为目前发现者的最优位置; xuj为最差位置; A为一个随机赋值1或-1的1×d矩阵，其中A+=AT(AAT)-1。
由于存在捕食者威胁，10%~20%的麻雀被随机选择作为侦察者，在捕食者出现时提醒整个种群做出反捕食行为。
xt+1ij={xtbest +β|xtij−xtbj|,fi≠fgxtij+K|xtij−xtwj|(fi−fw)+ε,fi=fg (3) 式中: xbest为当前全局最优位置; xbj为第j维的最优位置；β为步长因子，是均值为0、方差为1的正态分布的随机数; K∈rand[－1, 1]，fi为当前麻雀的适应度值; fg与fw为当前全局最佳与最差适应度值；ε是常数，防止分母为0。
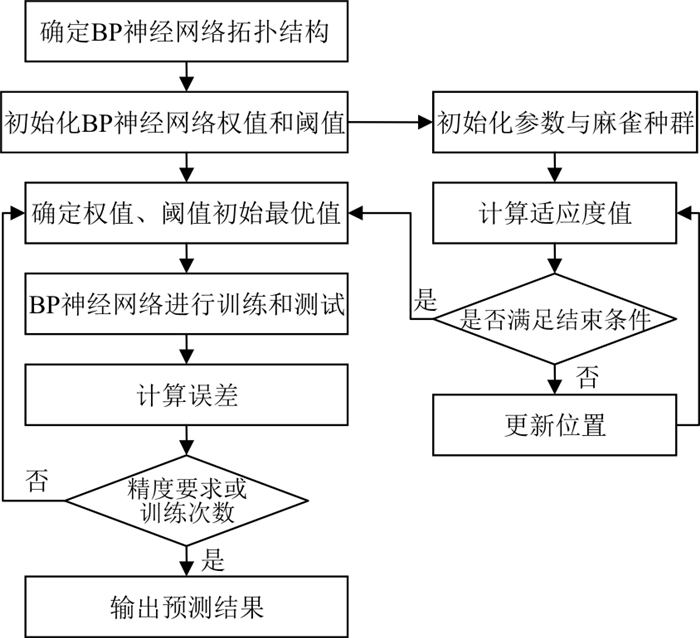
SSA-BP神经网络预测的流程如图 7所示。
3.1.3 基于PSO优化的BP神经网络
粒子群算法采用位置、速度与适应度值表示粒子特征[36], 通过个体极值与群体极值来确定最优位置。
在d维空间内，N个粒子组成的1个种群，找到个体极值与全局极值时，粒子进行速度更新与位置更新如下：
vt+1ij=wvtij+c1r1(ptej−xtij)+c2r2(ptgj−xtij)xt+1ij=xtij+vt+1ij (4) 式中: vij为第i个粒子在第j维的速度；c1, c2均为学习因子；r1, r2均为[0, 1]的随机数；pej为在第j维的个体极值；pgj为在第j维的全局极值。
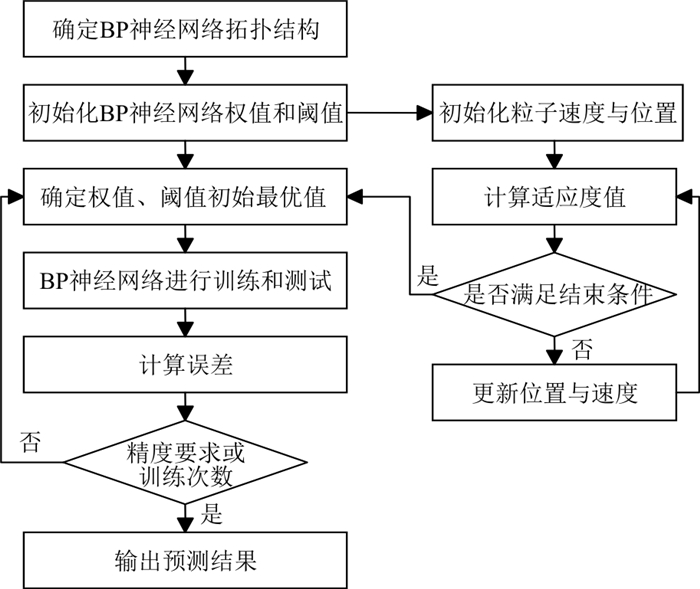
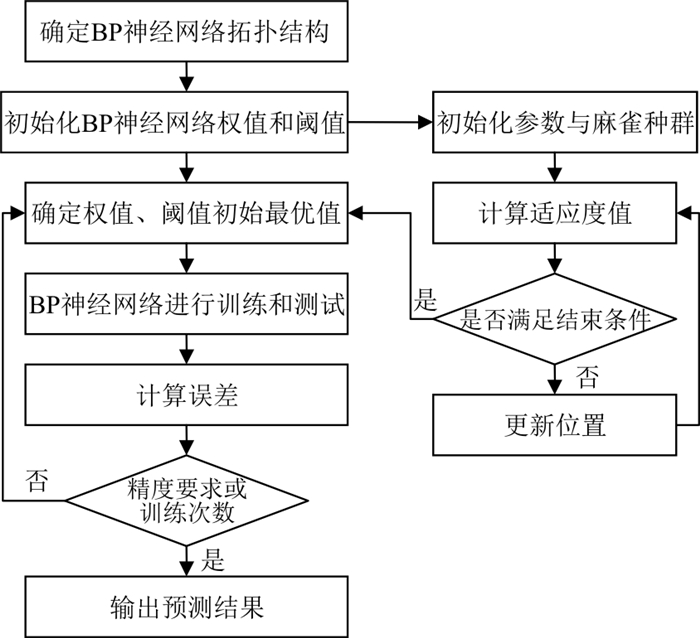
PSO-BP神经网络实质是将BP神经网络的权值和阈值映射为PSO粒子，通过对粒子速度和位置的更新迭代优化权值和阈值，从而提高BP神经网络的收敛速度和预测精度[37]。PSO-BP神经网络预测的流程如图 8所示。
3.2 影响因子的选取与构建
将选取的土层埋深、不均匀系数、曲率系数、天然含水量作为BP神经网络的输入，天然孔隙比作为输出，因此输入层节点个数O为4，输出层节点个数Q为1。
BP神经网络隐含层节点个数P按照经验公式[34]确定：$P=\sqrt{O+Q}+b $，b为1~10之间的常数，因此P的范围为3~12。综合考虑BP神经网络的收敛性能与泛化能力，确定隐含层节点个数为10。因此，BP神经网络为4-10-1的拓扑结构。在BP神经网络搭建过程中，隐含层分别采取Logsig函数和Tansig函数，输出层选择Purelin线性传递函数，其原因在于，通过所选取的4个输入指标预测天然孔隙比本质上是回归问题，不期望在输出层对数据进行处理。通过对比2类隐含层激活函数在验证集的表现，选择更好的函数搭配。训练函数采用Trainlm，训练次数为10 000，学习率为0.1，目标误差为10-6。根据BP神经网络的拓扑结构，SSA的种群规模为40，最大迭代次数100，ST取0.8，发现者占比20%。PSO的种群规模N为30，惯性权重为0.78，学习因子c1=c2=2，最大迭代次数为50。
3.3 预测结果与分析
利用构建的不同神经网络对太原市南内环东街站场地内黄土天然孔隙比进行预测。将室内试验实测数据分为训练集与验证集，随机选择实测数据的80%作为训练集，剩下的20%作为验证集。在此基础上增加训练集组数，探究样本数量对BP神经网络在验证集上的精度影响，选择训练集最佳样本数量，建立天然孔隙比预测模型，再利用验证集对模型的预测效果进行验证。同时，为了评估模型的最终泛化能力，选取地铁1号线沿线另一处典型黄土场地东太堡站，进一步收集3组天然黄土天然孔隙比及其影响因素的实测数据，作为测试集对模型进行测试。其中验证集与测试集数据见表 2。
表 2 天然孔隙比部分实测数据Table 2. Selected measured data for soil with natural void ratio类型 孔隙比 深度/m 曲率系数 不均匀系数 天然含水量/% 验证集 0.975 16 0.880 4 7.511 5 15.28 0.773 18 0.890 4 9.123 3 15.46 1.030 8 0.950 8 12.406 2 11.46 1.029 10 0.728 1 13.472 8 13.48 1.149 4 1.355 0 8.730 0 12.19 1.133 2 1.396 0 8.796 0 11.66 0.903 26 1.026 9 7.860 8 15.35 0.741 20 1.372 7 9.001 8 16.93 0.937 12 0.835 9 8.548 1 14.02 0.835 24 1.446 6 9.107 3 17.27 1.003 6 1.278 6 8.668 2 7.33 0.913 24 1.571 4 7.516 5 19.51 1.094 8 1.356 8 8.966 8 15.03 测试集 1.194 3.3 2.240 0 6.170 0 10.10 0.802 19.3 1.570 0 11.480 0 15.70 0.762 17.3 1.420 0 7.800 0 8.60 为确定不同隐含层激活函数对BP神经网络精度的影响，通过分别选择Logsig函数和Tansig函数，在训练集为80%的实测数据的模型框架中，研究BP神经网络的预测结果表现，如表 3所示。
表 3 隐含层激活函数对BP神经网络验证集预测结果影响Table 3. Influence of the hidden layer activation function on the BP neural network validation set predicted results隐含层函数 相关系数R2 均方误差MSE/% 平均绝对误差MAE/% 平均绝对百分比误差MAPE/% 纯均方误差MSPE/% Logsig 0.682 0.47 6.01 6.62 14.86 Tansig 0.729 0.40 5.64 6.16 13.57 根据表 3所示的结果，在隐含层函数为Tansig时，5个指标都有较为明显的提升，其中，相关系数(R2)提升比率为7%，均方误差(MSE)提升比率14.9%，平均绝对误差(MAE)提升比率为6.2%，平均绝对百分比误差(MAPE)提升比率为6.95%，纯均方误差(MSPE)提升比率为8.7%。由此可见，当隐含层函数为Tansig函数时，对于天然孔隙比的预测更为准确。因此，隐含层选择Tansig激活函数。
为确定不同训练集组数对BP神经网络预测效果的影响并选出最佳的训练集个数，通过增加样本数量，分别研究了训练集分别为51，52，53，54，55，56组时，BP神经网络的预测结果表现，如表 4所示。
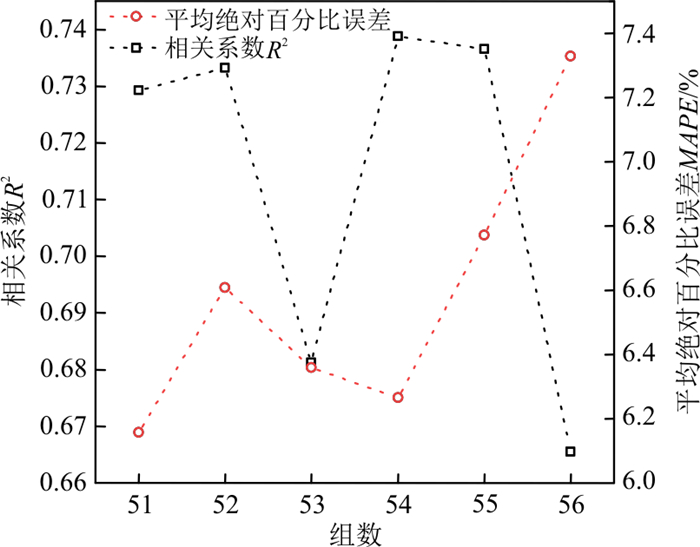
表 4 不同训练集组数下BP神经网络预测结果Table 4. Predicted results of the BP neural network under different numbers of trainings训练集组数 相关系数R2 均方误差MSE/% 平均绝对误差MAE/% 平均绝对百分比误差MAPE/% 纯均方误差MSPE/% 51 0.729 0.40 5.64 6.16 1.357 52 0.733 0.46 5.92 6.61 1.483 53 0.681 0.42 5.78 6.36 1.418 54 0.739 0.33 5.70 6.26 1.275 55 0.737 0.32 6.14 6.77 1.267 56 0.665 0.38 6.43 7.33 1.361 为更清楚地说明训练集组数对BP神经网络预测结果的影响，通过将验证集的数据增加至训练集中，改变训练集组数，由原来80%(51组)逐步增至87.5%(56组)，探究在不同训练组数下BP神经网络预测结果。选择相关系数R2和平均绝对百分比误差MAPE绘制预测结果随不同训练集组数图，如图 9所示。
图 9 不同训练集组数下验证集部分评价指标图Figure 9. Partial evaluation index chart of the validation set with different numbers of trainings当训练集从51组逐步增加至56组时，相关系数(R2)的变化并不是始终提升的，在训练集为54组时，相关系数(R2)提升最大，平均绝对百分比误差(MAPE)变化最小，相关系数(R2)从0.729提升至0.739，提升比率为1.3%。但平均绝对百分比误差(MAPE)从6.16%增至6.26%，下降比率为1.6%。综上可以发现，小幅度的提升训练集个数并不能显著增加BP神经网络在验证集上的精度。因此，综合考虑以51组为训练集搭建天然孔隙比预测模型。
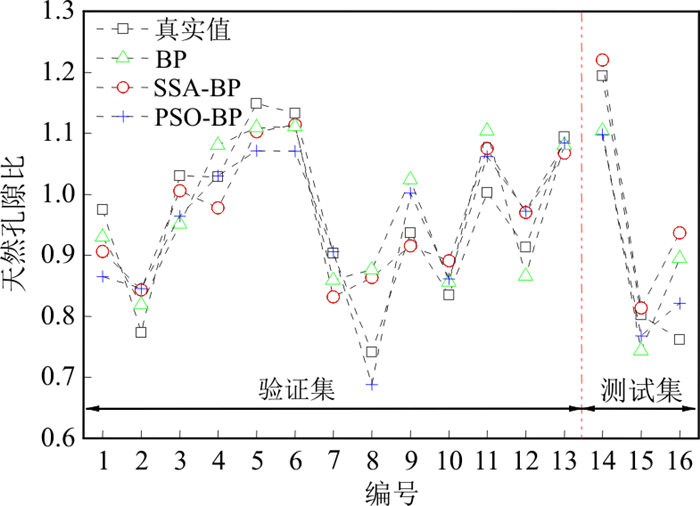
为定量评价基于神经网络的天然孔隙比预测模型的可靠性，保证3种方法的训练集与验证集一致，采用训练后的BP神经网络、SSA-BP神经网络和PSO-BP神经网络对20%的验证样本以及3组测试样本进行了预测，结果如图 10所示。
图 10 天然孔隙比预测值与真实值对比图Figure 10. Compared values of predicted and measured natural void ratio将预测结果与实际测量结果进行对比，采用相关系数(R2)、均方误差(MSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、纯均方误差(MSPE)5个指标对预测结果准确性进行评价，具体结果见表 5。从预测结果来看，PSO-BP神经网络的相关系数在验证集与测试集中均为最高，其中在验证集中相关系数为0.772，测试集中为0.946；SSA-BP神经网络相较于BP神经网络的提升效果不明显，验证集中各项评价指标与BP神经网络差别很小，且在测试集中，SSA-BP神经网络的均方误差与纯均方误差大于BP神经网络，表明麻雀算法的提升效果不稳定，泛化能力较弱；而PSO-BP神经网络的评价指标值均有显著提高。结果表明PSO-BP的神经网络预测模型优于SSA-BP神经网络和BP神经网络，可以有效预测天然孔隙比。
表 5 BP神经网络、SSA-BP神经网络、PSO-BP神经网络预测结果Table 5. Predicted results of the BP neural network, SSA-BP neural network, PSO-BP neural network类型 预测方法 相关系数R2 均方误差MSE/% 平均绝对误差MAE/% 平均绝对百分比误差MAPE/% 纯均方误差MSPE/% 验证集 BP神经网络 0.729 0.40 5.64 6.16 13.57 SSA-BP神经网络 0.769 0.35 5.45 6.05 12.97 PSO-BP神经网络 0.772 0.33 5.12 5.41 11.39 测试集 BP神经网络 0.756 0.21 9.39 10.77 10.19 SSA-BP神经网络 0.860 0.22 7.08 8.86 11.53 PSO-BP神经网络 0.946 0.09 6.33 6.71 6.00 4. 结论
(1) Q3黄土与Q2黄土的颗粒级配相似，呈单峰型分布特征，40~50 μm粒径含量最高，且其微分含量均大于10%。古土壤3~20 μm粒径的颗粒含量相较于黄土有显著增加，且随深度增加细颗粒含量有增大趋势。在物质组成方面，黄土层与古土壤层近似一致。
(2) 天然孔隙比具有随深度增加而减小的整体趋势。但由于地层情况不同，孔隙比在各个地层受到的主要影响因素也有所不同。黄土层天然孔隙比受应力历史主导，同时含水状态也可能是天然孔隙比变化的原因之一，古土壤层天然孔隙比受粒径分布主导。
(3) 天然孔隙比与应力历史、颗粒级配和水力历史有关。土层埋深是作为反映应力历史的重要指标，不均匀系数以及曲率系数是反映颗粒级配的重要指标，天然含水量是反映水力历史的重要指标。因此，天然孔隙比定量评价的影响因素可确定为土层埋深、不均匀系数、曲率系数和天然含水量。
(4) 根据选取的天然孔隙比影响因素以及实测数据，采用SSA算法与PSO算法对BP神经网络的初始权值、阈值进行优化，建立基于SSA-BP与PSO-BP神经网络的预测模型，能够解决BP神经网络陷入局部极小的问题，提高了天然孔隙比的预测精度。其中PSO-BP神经网络的优化效果高于SSA-BP神经网络，能够有效预测天然孔隙比。
(所有作者声明不存在利益冲突) -
图 3 粒径级配曲线
a.T0探井粒径微分质量分数曲线; b.T0探井累计质量分数曲线; c.T5探井粒径微分质量分数曲线; d. T5探井累计质量分数曲线; e.T8探井粒径微分质量分数曲线; f.T8探井累计质量分数曲线
Figure 3. Particle size distribution curves
图 4 Q3黄土(a)、古土壤(b)以及Q2黄土(c)的XRD曲线
Figure 4. XRD curves of Q3 loess(a), paleosols (b) and Q2 loess (c)
图 5 天然孔隙比与Q3黄土、古土壤和Q2黄土的固结曲线
Figure 5. Natural void ratio and consolidation curves of Q3 loess, paleosols and Q2 loess
图 6 天然孔隙比随天然含水量变化散点图
Figure 6. Scatter plot of the natural void ratio versus water content
图 9 不同训练集组数下验证集部分评价指标图
Figure 9. Partial evaluation index chart of the validation set with different numbers of trainings
图 10 天然孔隙比预测值与真实值对比图
Figure 10. Compared values of predicted and measured natural void ratio
表 1 一维固结试验方案
Table 1. One-dimensional consolidation test scheme
土层类型 固结压力/kPa Q3黄土 14.35, 64.40, 120.45, 222 古土壤 259, 333 Q2黄土 370, 480 
下载: 导出CSV
表 2 天然孔隙比部分实测数据
Table 2. Selected measured data for soil with natural void ratio
类型 孔隙比 深度/m 曲率系数 不均匀系数 天然含水量/% 验证集 0.975 16 0.880 4 7.511 5 15.28 0.773 18 0.890 4 9.123 3 15.46 1.030 8 0.950 8 12.406 2 11.46 1.029 10 0.728 1 13.472 8 13.48 1.149 4 1.355 0 8.730 0 12.19 1.133 2 1.396 0 8.796 0 11.66 0.903 26 1.026 9 7.860 8 15.35 0.741 20 1.372 7 9.001 8 16.93 0.937 12 0.835 9 8.548 1 14.02 0.835 24 1.446 6 9.107 3 17.27 1.003 6 1.278 6 8.668 2 7.33 0.913 24 1.571 4 7.516 5 19.51 1.094 8 1.356 8 8.966 8 15.03 测试集 1.194 3.3 2.240 0 6.170 0 10.10 0.802 19.3 1.570 0 11.480 0 15.70 0.762 17.3 1.420 0 7.800 0 8.60
下载: 导出CSV
表 3 隐含层激活函数对BP神经网络验证集预测结果影响
Table 3. Influence of the hidden layer activation function on the BP neural network validation set predicted results
隐含层函数 相关系数R2 均方误差MSE/% 平均绝对误差MAE/% 平均绝对百分比误差MAPE/% 纯均方误差MSPE/% Logsig 0.682 0.47 6.01 6.62 14.86 Tansig 0.729 0.40 5.64 6.16 13.57
下载: 导出CSV
表 4 不同训练集组数下BP神经网络预测结果
Table 4. Predicted results of the BP neural network under different numbers of trainings
训练集组数 相关系数R2 均方误差MSE/% 平均绝对误差MAE/% 平均绝对百分比误差MAPE/% 纯均方误差MSPE/% 51 0.729 0.40 5.64 6.16 1.357 52 0.733 0.46 5.92 6.61 1.483 53 0.681 0.42 5.78 6.36 1.418 54 0.739 0.33 5.70 6.26 1.275 55 0.737 0.32 6.14 6.77 1.267 56 0.665 0.38 6.43 7.33 1.361
下载: 导出CSV
表 5 BP神经网络、SSA-BP神经网络、PSO-BP神经网络预测结果
Table 5. Predicted results of the BP neural network, SSA-BP neural network, PSO-BP neural network
类型 预测方法 相关系数R2 均方误差MSE/% 平均绝对误差MAE/% 平均绝对百分比误差MAPE/% 纯均方误差MSPE/% 验证集 BP神经网络 0.729 0.40 5.64 6.16 13.57 SSA-BP神经网络 0.769 0.35 5.45 6.05 12.97 PSO-BP神经网络 0.772 0.33 5.12 5.41 11.39 测试集 BP神经网络 0.756 0.21 9.39 10.77 10.19 SSA-BP神经网络 0.860 0.22 7.08 8.86 11.53 PSO-BP神经网络 0.946 0.09 6.33 6.71 6.00
下载: 导出CSV
-
[1] 张炜, 张苏民. 非饱和黄土的结构强度特性[J]. 水文地质工程地质, 1990, 17(4): 22-25, 49.Zhang W, Zhang S M. Structural strength characteristics of unsaturated loess[J]. Hydrogeology & Engineering Geology, 1990, 17(4): 22-25, 49(in Chinese with English abstract). [2] 姜高磊, 刘林敬, 毕志伟, 等. 河北丰宁黄土粒度特征及其环境意义[J]. 地质科技情报, 2018, 37(4): 83-89. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201804011.htmJiang G L, Liu L J, Bi Z W, et al. Grain-size characteristics and its environmental significance of loess in Fengning, Hebei Province[J]. Geological Science and Technology Information, 2018, 37(4): 83-89(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201804011.htm [3] 党进谦, 李靖. 非饱和黄土的结构强度与抗剪强度[J]. 水利学报, 2001, 32(7): 79-83, 90.Dang J Q, Li J. Structural strength and shear strength of unsaturated loess[J]. Journal of Hydraulic Engineering, 2001, 32(7): 79-83, 90(in Chinese with English abstract). [4] 张伯平, 王力, 袁海智. 含水量对黄土结构强度影响的定量分析[J]. 西北农业大学学报, 1994, 22(1): 54-60.Zhang B P, Wang L, Yuan H Z. Quantitative analysis of influence of water content on structural strength of loess[J]. Journal of Northwest Agricultural University, 1994, 22(1): 54-60(in Chinese with English abstract). [5] 冯立, 张茂省, 胡炜, 等. 黄土垂直节理细微观特征及发育机制探讨[J]. 岩土力学, 2019, 40(1): 235-244.Feng L, Zhang M S, Hu W, et al. Discussion on microscopic, microcosmic characteristics and developmental mechanism of loess vertical joints[J]. Rock and Soil Mechanics, 2019, 40(1): 235-244(in Chinese with English abstract). [6] 罗浩, 伍法权, 常金源, 等. 马兰黄土孔隙结构特征: 以赵家岸地区黄土为例[J]. 工程地质学报, 2021, 29(5): 1366-1372.Luo H, Wu F Q, Chang J Y, et al. Pore characteristics of Malan loess: A case study at Zhaojia'an landslide[J]. Journal of Engineering Geology, 2021, 29(5): 1366-1372(in Chinese with English abstract). [7] 田堪良, 王沛, 张慧莉. 考虑结构性的原状黄土应力-应变关系的探讨[J]. 岩土力学, 2013, 34(7): 1893-1898.Tian K L, Wang P, Zhang H L. Discussion on stress-strain relation of intact loess considering soil structure[J]. Rock and Soil Mechanics, 2013, 34(7): 1893-1898(in Chinese with English abstract). [8] Jiang M, Zhang F, Hu H, et al. Structural characterization of natural loess and remolded loess under triaxial tests[J]. Engineering Geology, 2014, 181: 249-260. doi: 10.1016/j.enggeo.2014.07.021 [9] 郑佳, 庄建琦, 孔嘉旭, 等. 基于CT扫描的黄土孔隙结构特征研究[J]. 地质科技通报, 2022, 41(6): 211-222. doi: 10.19509/j.cnki.dzkq.2022.0210Zheng J, Zhuang J Q, Kong J X, et al. Study on pore structure characteristics of loess based on CT scanning[J]. Bulletin of Geological Science and Technology, 2022, 41(6): 211-222(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2022.0210 [10] 李泽坤, 马鹏辉, 彭建兵, 等. 黑方台地区马兰黄土渗透特性及结构损伤试验研究[J]. 地质科技通报, 2022, 41(6): 200-210. doi: 10.19509/j.cnki.dzkq.2022.0251Li Z K, Ma P H, Peng J B, et al. Experimental study on permeability characteristics and structural damage of Malan loess in Heifangtai area[J]. Bulletin of Geological Science and Technology, 2022, 41(6): 200-210(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2022.0251 [11] 井旭, 谢婉丽, 单帅. 原状及重塑黄土双轴试验微观力学特征离散元模拟[J]. 地质科技通报, 2021, 40(3): 184-193. doi: 10.19509/j.cnki.dzkq.2021.0311Jing X, Xie W L, Shan S. Discrete element simulation study on micromechanical characteristics of undisturbed and remolded loess in biaxial test[J]. Bulletin of Geological Science and Technology, 2021, 40(3): 184-193(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2021.0311 [12] 井彦林. 基于数据挖掘技术的黄土湿陷性研究[D]. 西安: 西安理工大学, 2006.Jing Y L. Study on loess collapsibility based on data mining[D]. Xi 'an: Xi 'an University of Technology, 2006(in Chinese with English abstract). [13] 马闫, 王家鼎, 彭淑君, 等. 黄土湿陷性与土性指标的关系及其预测模型[J]. 水土保持通报, 2016, 36(1): 120-128.Ma Y, Wang J D, Peng S J, et al. Relationship between physical-mechanical parameters and collapsibility of loess soil and its prediction model[J]. Bulletin of Soil and Water Conservation, 2016, 36(1): 120-128(in Chinese with English abstract). [14] 叶为民, 崔玉军, 黄雨, 等. 黄土的湿陷性及其评价准则[J]. 岩石力学与工程学报, 2006, 35(3): 550-556. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200603021.htmYe W M, Cui Y J, Huang Y, et al. Collapsibility of loess and its discrimination criteria[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 35(3): 550-556(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200603021.htm [15] 徐志军, 郑俊杰, 张军, 等. 聚类分析和因子分析在黄土湿陷性评价中的应用[J]. 岩土力学, 2010, 31(增刊2): 407-411. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2010S2073.htmXu Z J, Zheng J J, Zhang J, et al. Application of cluster analysis and factor analysis to evaluation of loess collapsibility[J]. Rock and Soil Mechanics, 2010, 31(S2): 407-411(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2010S2073.htm [16] 高凌霞, 栾茂田, 杨庆. 基于微结构参数主成分的黄土湿陷性评价[J]. 岩土力学, 2012, 33(7): 1921-1926. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201207002.htmGao L X, Luan M T, Yang Q. Evaluation of loess collapsibility based on principal components of microstructural parameters[J]. Rock and Soil Mechanics, 2012, 33(7): 1921-1926(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201207002.htm [17] Xu L, Coop M R. The mechanics of a saturated silty loess with a transitional mode[J]. Géotechnique, 2017, 67(7): 581-596. [18] Xu L, Gao C, Lan T, et al. Influence of grading on the compressibility of saturated loess soils[J]. Géotechnique Letters, 2020, 10(2): 198-204. [19] Zuo L, Xu L, Baudet B A, et al. The structure degradation of a silty loess induced by long-term water seepage[J]. Engineering Geology, 2020, 272: 105634. [20] Paz-Ferreiro J, Vázquez E V, Miranda J G V. Assessing soil particle-size distribution on experimental plots with similar texture under different management systems using multifractal parameters[J]. Geoderma, 2010, 160(1): 47-56. [21] 谢远云, 李长安, 何葵, 等. 青海省民和黄土的粒度组成及气候含义[J]. 地质科技情报, 2002, 21(2): 41-44. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ200202008.htmXie Y Y, Li C A, He K, et al. Climatic implication and grains size composition from Minhe loess in Qinghai Province[J]. Geological Science and Technology Information, 2002, 21(2): 41-44(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ200202008.htm [22] Sun J. Provenance of loess material and formation of loess deposits on the Chinese Loess Plateau[J]. Earth and Planetary Science Letters, 2002, 203(3/4): 845-859. [23] Li Y, Shi W, Aydin A, et al. Loess genesis and worldwide distribution[J]. Earth-Science Reviews, 2020, 201: 102947. [24] Liu Z, Liu F, Ma F, et al. Collapsibility, composition, and microstructure of loess in China[J]. Canadian Geotechnical Journal, 2016, 53(4): 673-686. [25] Derbyshire E. Geological hazards in loess terrain, with particular reference to the loess regions of China[J]. Earth-Science Reviews, 2001, 54(1/3): 231-260. [26] 曹宇清, 吴永, 安向勇, 等. 考虑应力历史和应力水平影响的土体压缩模量计算方法[J]. 工程地质学报, 2019, 27(4): 760-765. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201904009.htmCao Y Q, Wu Y, An X Y, et al. Calculation method of soil compression modulus considering the influence of stress history and stress level[J]. Journal of Engineering Geology, 2019, 27(4): 760-765(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201904009.htm [27] Estabragh A R, Javadi A A, Boot J C. Effect of compaction pressure on consolidation behaviour of unsaturated silty soil[J]. Canadian Geotechnical Journal, 2004, 41(3): 540-550. [28] Chang C S, Deng Y, Yang Z. Modeling of minimum void ratio for granular soil with effect of particle size distribution[J]. Journal of Engineering Mechanics, 2017, 143(9): 04017060. [29] Xu Z, Xu N, Wang H. Effects of particle shapes and sizes on the minimum void ratios of sand[J]. Advances in Civil Engineering, 2019, 2019: 5732656. [30] 简涛, 李喜安, 王力, 等. 颗粒组构对黄土压缩特性及其粒间状态的影响[J]. 科学技术与工程, 2018, 18(30): 212-219.Jian T, Li X A, Wang L, et al. Effect of grain fabric on compressive properties and intergranular state of loess[J]. Science Technology and Engineering, 2018, 18(30): 212-219(in Chinese with English abstract). [31] 杨坪, 吴民晖, 许德鲜. 含水率对重塑黄土的变形特性影响的实验研究[J]. 工程地质学报, 2015, 23(6): 1066-1071. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201506006.htmYang P, Wu M H, Xu D X. Experimental study on the effect of water content on deformation characteristics of remolded loess[J]. Journal of Engineering Geology, 2015, 23(6): 1066-1071(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201506006.htm [32] 张晓周, 卢玉东, 李鑫, 等. 增湿条件下泾阳南塬马兰黄土孔隙率变化研究[J]. 干旱区资源与环境, 2019, 33(6): 99-104.Zhang X Z, Lu Y D, Li X, et al. The change of Malan loess porosity in south Jingyang Plateau under humidification condition[J]. Journal of Arid Land Resources and Environment, 2019, 33(6): 99-104(in Chinese with English abstract). [33] Russell A R. How water retention in fractal soils depends on particle and pore sizes, shapes, volumes and surface areas[J]. Géotechnique, 2014, 64(5): 379-390. [34] 沈花玉, 王兆霞, 高成耀, 等. BP神经网络隐含层单元数的确定[J]. 天津理工大学学报, 2008, 91(5): 13-15. https://www.cnki.com.cn/Article/CJFDTOTAL-TEAR200805006.htmShen H Y, Wang Z X, Gao C Y, et al. Determination the number of BP neural network hidden layer units[J]. Journal of Tianjin University of Technology, 2008, 91(5): 13-15(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-TEAR200805006.htm [35] 薛建凯. 一种新型的群智能优化技术的研究与应用[D]. 上海: 东华大学, 2020.Xue J K. Research and application of a novel swarm intelligence optimization technique: Sparrow search algorithm[D]. Shanghai: Donghua University, 2020(in Chinese with English abstract). [36] Zhang W, Gu X, Tang L, et al. Application of machine learning, deep learning and optimization algorithms in Geoengineering and Geoscience: Comprehensive review and future challenge[J]. Gondwana Research, 2022, 109: 1-17. [37] 涂娟娟. PSO优化神经网络算法的研究及其应用[D]. 江苏镇江: 江苏大学, 2020.Tu J J. Research onlearning algorithm of neural network optimized with PSO and its application[D]. Zhenjiang Jiangsu: Jiangsu University, 2020(in Chinese with English abstract). 期刊类型引用(0)
其他类型引用(1)
-
下载:
下载:
点击查看大图
计量
- 文章访问数: 880
- PDF下载量: 57
- 被引次数: 1
