Axisymmetric simplified method for stability analysis of an circular-like mine slope
-
摘要:
为响应国家“绿水青山就是金山银山”的发展理念, 对废弃矿坑的开发再利用成为热点, 而采用合理的稳定性评价方法对废弃矿坑边坡加固设计是后续工作的关键。但这类矿坑边坡通常形状近似圆形或椭圆形, 三维空间效应不容忽略, 基于传统平面应变假设的简化方法对其进行稳定性分析似乎不太合理。在FLAC3D强度折减法的基础上, 提出了一种针对近似圆形矿坑边坡稳定性分析的轴对称模型简化计算方法。基于计算结果的对比分析表明:①对于这种类似圆形凹坡, 轴对称模型计算的安全系数比传统平面应变模型更准确, 减少了计算时间, 并且轴对称模型对于各种复杂程度不同的边坡类型同样适用;②轴对称模型计算的安全系数与三维模型计算的安全系数非常接近, 而传统平面应变模型计算的安全系数偏于保守;③将轴对称模型计算结果与现有研究对比, 表明两者结果相符, 并将其进一步应用于长沙冰雪世界项目矿坑边坡加固工程的稳定性分析中, 证明其可为类似工程的边坡稳定性评价提供参考。
Abstract:To follow the national development concept of "Lucid waters and lush mountains are invaluable assets", the reuse of abandoned mines has become a hotspot. A reasonable stability analysis method to reinforce the slope must be proposed. However, the shape of common mine slope is close to a circle or an ellipse, and thus the three-dimensional space effect of stability cannot be ignored. Based on the strength reduction method of FLAC3D, an axisymmetric numerical analysis method was proposed. Through comparative calculation and analysis, some conclusions can be obtained as follows: (1)For concave slopes with circular-likeshape, the safety factor calculated by the axisymmetric model is more accurate than that of the traditional plane strain model, the calculation time of the proposed model is less, and the proposed model is also applicable to various types of slopes. (2)The safety factor obtained from the axisymmetric model is close to the results obtained from the 3-D model, while the safety factor obtained from the traditional plane strain model is conservative.(3)The calculation results of the axisymmetric model are also consistent with the results from the literature. The proposed model is further applied to the stability analysis of a mine slope reinforcement in Changsha Ice World, which can also be applied in the slope stability evaluation of similar projects.
-
Key words:
- mine slope /
- FLAC3D /
- axisymmetric model /
- plane strain model
-
资源开发利用为国民经济快速发展提供了保障, 同时也对人类生存环境造成了不同程度的破坏, 露天资源开采形成的众多高陡岩质边坡是其典型代表, 资源开发完成后遗留下来的采场积水成渊, 导致地表环境持续恶化, 成为社会公害。“绿水青山就是金山银山”为新时代[1]正确处理经济发展与环境修复和保护指明了方向, 对废弃采场进行生态修复或者二次开发再利用成为国家的战略目标, 符合国家“可持续发展”的科学理念。在对废弃采场开发再利用的过程中, 对采场边坡进行稳定性评价及加固治理是重中之重, 是后续工程正常进行的前提, 需要采用科学合理的分析方法。
常用的边坡稳定性计算方法主要有两大类[2-3]:极限平衡法和强度折减法。极限平衡法应用最早, 其原理是将超静定的滑坡失稳问题引入部分假设条件后转化为静定问题, 从而进行求解。强度折减法是在计算机技术发展下出现的一种边坡稳定性数值计算方法, 现已被广泛使用。强度折减法相比于极限平衡法有较多优势:首先, 强度折减法考虑了应力应变之间的本构关系和变形协调条件, 计算结果相对准确;其次, 强度折减法能够模拟边坡的变形过程和滑动面形状而不需要对滑动面进行假设;最后, 强度折减法能够对复杂地貌、地质构造的边坡进行计算。在稳定性分析时, 分析模式均可分为二维分析[4-7]和三维分析[8-10], 二维分析是以弹性力学中平面应变问题为基础, 假定坡体只受平行于横截面方向上的面力或约束[11], 从而将三维空间问题转化为平面问题, 边坡的稳定性可用边坡典型断面的稳定性来代替, 简化了计算。三维分析模式是弹性力学三维空间问题在工程中的完全应用, 通过建立区域所在的整体三维模型, 加上特定初始条件和边界条件, 求得与真实情况相符的整体边坡最小安全系数, 对边坡稳定性做出合理评价。采用二维分析模式对边坡稳定性进行评价时, 计算速度快、效率高, 能辅助快速进行边坡的加固设计, 但由于二维分析模式是以平面应变问题为前提的, 故适用于一些坡面形态平直的边坡类型, 而对于这类废弃采场边坡, 由于资源开采工程的特点, 其坡面形态往往为近似圆形的凹形边坡, 三维空间效应对边坡稳定性的影响[12]不可忽略, 因而采用三维分析模式是较好的选择。针对坡面形态对边坡稳定性的影响这一问题, Baker等[13]研究了凸形边坡的曲率半径R与坡高H之比变化时边坡稳定性的变化, 发现随R/H的增大凸形边坡的稳定性逐渐降低。王家臣等[14]建立了考虑水平凸形边坡破坏机理的边坡稳定性三维极限平衡方法, 研究了坡面形态的相对曲率半径对凸形边坡稳定性的影响。赵衡等[15]认为圆形凸坡的破坏模式接近于轴对称破坏, 并提出了轴对称破坏模式下圆形凸坡安全系数的极限平衡法, 纠正了以往对平面应变模式计算圆形凸坡安全系数偏于不安全的认识。卢坤林等[16]通过资料统计分析、模型试验和理论计算等方法对凸坡、平坡和凹坡的稳定性进行了研究, 得出了凸形边坡稳定性较差而凹形边坡稳定性较好的结论。
上述研究者在不同坡面形态下边坡的三维稳定性方面做了大量探索, 提出了凸形边坡考虑空间形状效应的三维稳定性分析方法, 但三维分析模式计算耗时较长, 无法在边坡加固设计时对边坡稳定性进行快速评价。尤其在采用有限元强度折减法时, 模型的单元数量会导致计算时间成倍增加, 效率极低。但若采用二维分析模式, 即采用平面应变假定来简化, 对于坡面形态近似圆形的边坡类型可能会产生较大的误差。笔者针对圆形凹坡的稳定性分析, 采用强度折减法并借助FLAC3D软件, 提出一种考虑凹形边坡三维空间效应, 将三维数值模型按轴对称问题简化为二维数值模型的计算方法。相比于二维平面应变简化计算模式, 该方法计算的安全系数更加接近三维计算模式, 并且计算时间比三维计算模式大幅缩短。
1. 轴对称模型简化计算方法
1.1 模型建立
FLAC3D软件内置强度折减法是工程中常用的一种边坡稳定性分析方法, 该方法主要以数值计算的收敛性作为边坡失稳的依据[17], 其精度被工程行业所接受。在边坡稳定性分析时, 为提高计算效率, 一般在整个边坡体中取部分典型剖面, 建立边坡的二维数值模型, 以平面应变问题计算边坡的安全系数, 这种计算方法在坡体纵向尺寸较大时(即长直坡类型)无疑是合理的, 但对于形状近似于圆形的边坡, 若仍以平面应变问题来简化处理, 显然与弹性力学中平面应变问题的前提条件不符, 计算得到的安全系数可能存在较大误差。为此, 根据这类近似圆形边坡的几何形状、约束情况及受力特点, 结合弹性力学中的轴对称问题, 建立以轴对称简化后的二维计算模型。
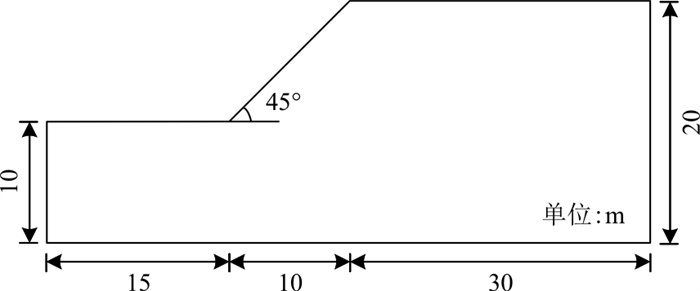
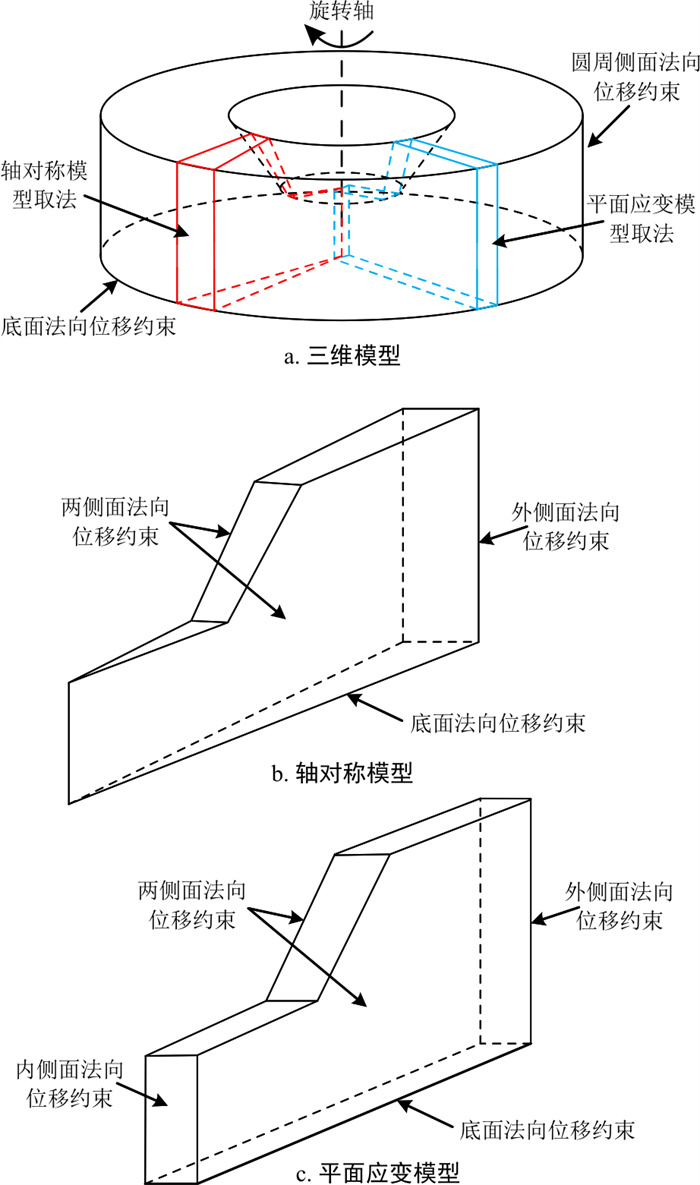
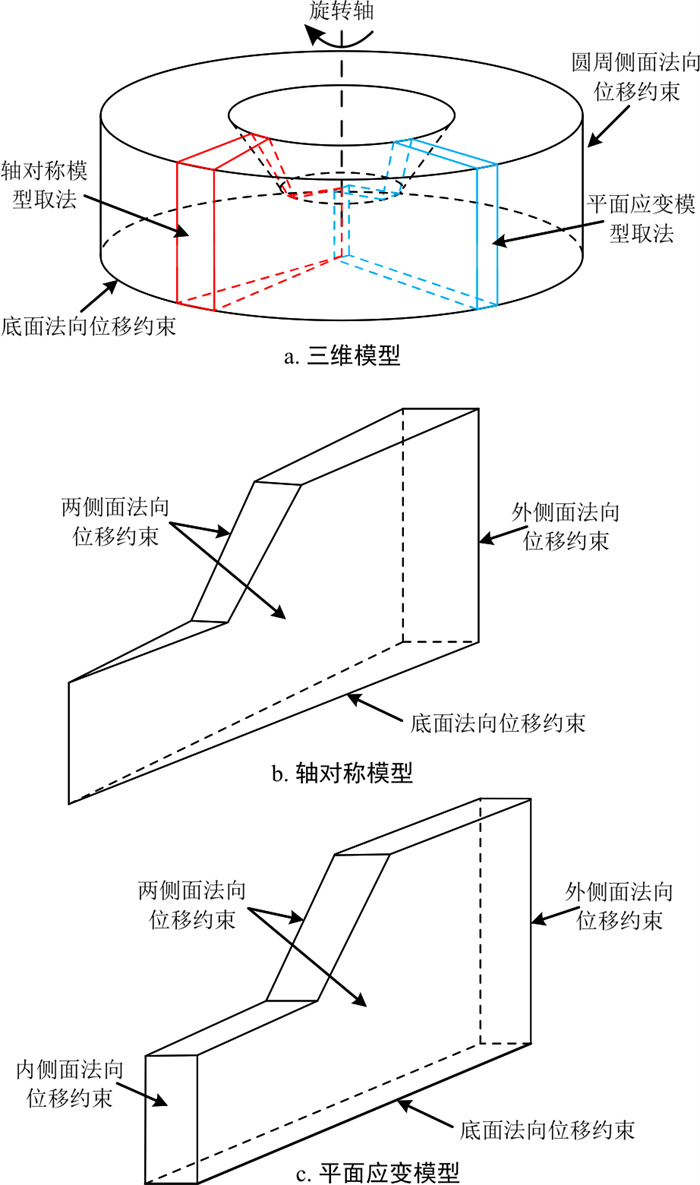
根据文献[18]中对强度折减法计算边坡安全系数时数值模型边界范围的优化结论, 建立坡角β=45°、坡高H=10 m的边坡模型, 以得到最优的计算精度, 边坡尺寸示意如图 1所示。根据该边坡尺寸, 以左侧边界为旋转中心轴旋转360°建立三维圆形凹坡数值模型, 该三维模型为完全均质的, 以下简称其为“三维模型”,如图 2-a所示。本研究轴对称简化二维模型的建立方法为:以三维模型为基础, 类似于轴对称问题基本方程的推导中单元体的取法[10], 从三维模型中心向外引2条射线, 以这2条射线在三维模型中切割出的楔形建立二维计算模型, 如图 2-a中红线所示, 最终得到完整的轴对称简化二维模型,如图 2-b所示, 以下简称其为“轴对称模型”。同时建立普通平面应变简化的二维计算模型, 以下简称“平面应变模型”, 如图 2-c所示。本研究所建立的轴对称模型与普通平面应变模型的本质区别在于边界条件设置的不同, 如图 2-b, c所示, 轴对称简化模型只存在3个侧面, 分别约束了3个侧面的法向位移, 这与三维模型中过中心任取的楔形体受力情况最接近, 而平面应变模型则有4个侧面, 分别约束了4个侧面的法向位移。
1.2 边界条件及本构参数
三维模型边界条件为模型圆周侧面法向位移约束, 底部法向位移约束, 其他面为自由面;轴对称模型边界条件为楔形体两侧面及外侧面法向位移约束, 底部法向位移约束, 其他面为自由面;平面应变模型边界条件为两侧面及内、外侧面法向位移约束, 底部法向位移约束, 其他面为自由面。计算土体用摩尔-库伦本构模型, 图 1所示边坡采用的力学参数如表 1所示。
表 1 土体力学参数表Table 1. Mechanical parameters of soil密度ρ/ (kg∙m-3) 弹性模量E/GPa 泊松比μ 黏聚力c/kPa 内摩擦角φ/(°) 2 400 4.3 0.2 28 27 1.3 结果验证
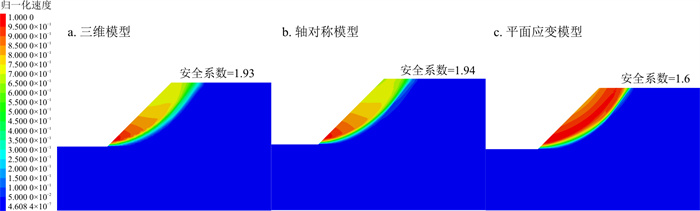
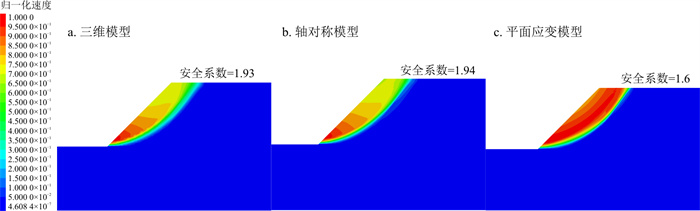
根据上文建立的模型, 分别计算3种模型的安全系数, 并得到临界状态下的速度云图。当边坡发生临界滑动时, 滑体内各点速度应大于0, 而其他稳定区域的速度应等于0。由于不同模型处于临界状态时的折减系数不同, 无法比较其数值的大小关系, 故只将各速度云图进行归一化(将模型中各点速度除以最大速度)后比较变化趋势。图 3分别为3种模型中间剖面归一化后的速度云图及相应安全系数, 可以看出, 采用本文所述方法建立的轴对称模型计算的边坡安全系数与三维模型计算得到的安全系数非常接近, 相差仅0.01, 说明了本文提出的简化模型的合理性。而相同条件下平面应变模型计算的安全系数相比于三维模型来说偏小且差距较大, 相差达0.33。另外通过归一化后的速度云图也可看出, 轴对称模型的速度变化趋势与三维模型的变化趋势趋于一致, 即坡脚处首先发生滑动进而引起坡脚以上部分滑体发生滑动, 而平面应变模型的速度变化趋势则与三维模型差异较大, 这更加说明了本文所提出的轴对称模型与三维模型受力的相似性。
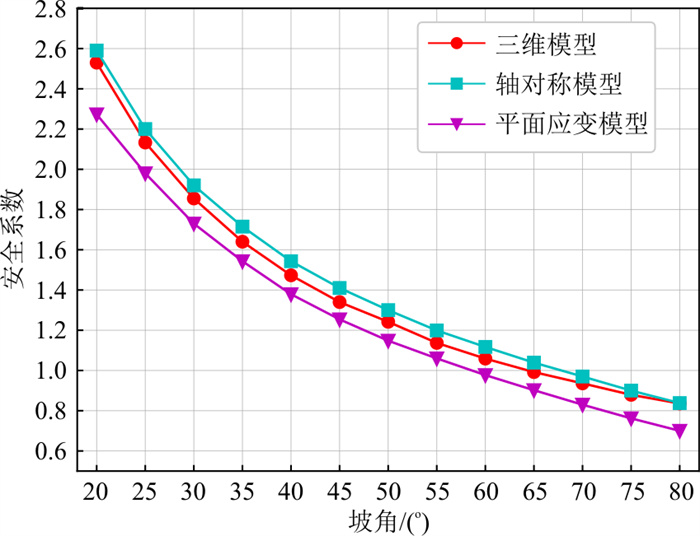
为进一步验证轴对称模型的合理性, 分别建立了不同坡角β的三维模型、轴对称模型和平面应变模型, 计算其安全系数, 以得到坡角变化时3种模型安全系数的差异。如图 4所示为3种模型计算的安全系数随边坡坡角变化曲线, 由曲线可知随着坡角增大边坡安全系数逐渐降低, 轴对称模型的安全系数与三维模型的安全系数更接近, 而平面应变模型的安全系数与三维模型的安全系数差距较大, 且其数值整体比三维模型偏小。
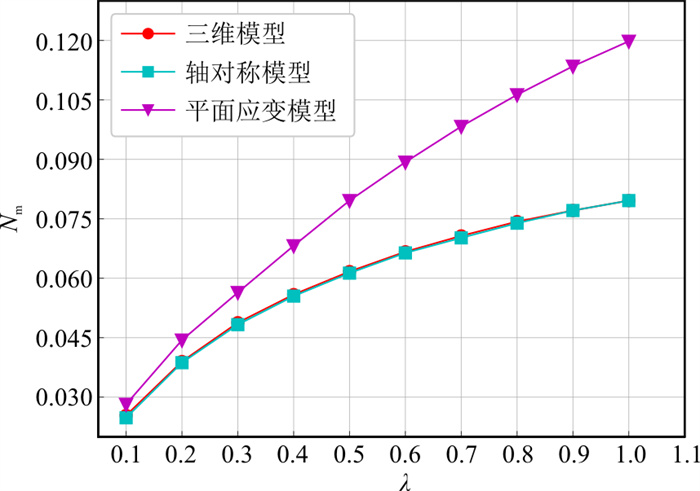
以上分析均基于一组相同的土体参数, 为此引入无量纲常数[6]Nm和λ, 以分析土体参数变化时, 3种模型安全系数的差异。Nm为无量纲化后安全系数的倒数, λ为考虑土体参数变化的无量纲化常数, 其定义分别为:
Nm=cFtrial ⋅1γH (1) λ=cγHtanφ (2) 式中:Ftrial为安全系数;γ为土体重度;H为坡高;c为黏聚力;φ为内摩擦角。
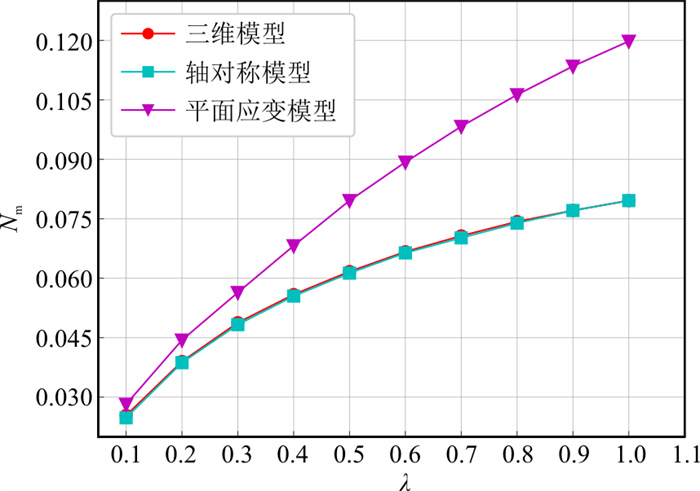
土体参数λ分别取为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0。图 5给出了3种模型Nm随λ的变化曲线, 可知在土体参数变化的情况下轴对称模型与三维模型计算的安全系数几乎一致, 而平面应变模型计算的结果与三维模型计算的结果差距较大, 并且这种差距随着土体参数Nm, λ的变大而增大, 所得结论与文献[13]相同。
1.4 复杂边坡模型分析
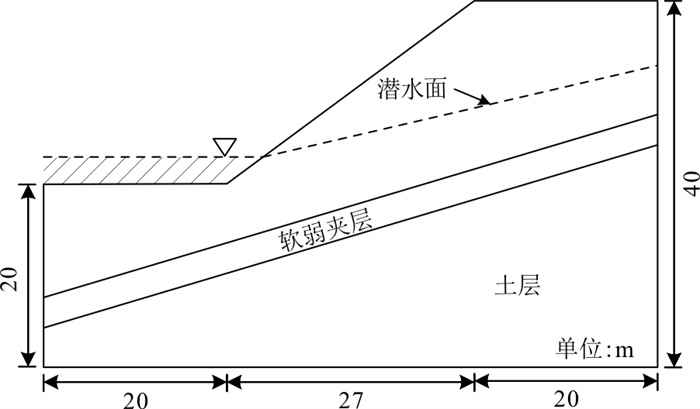
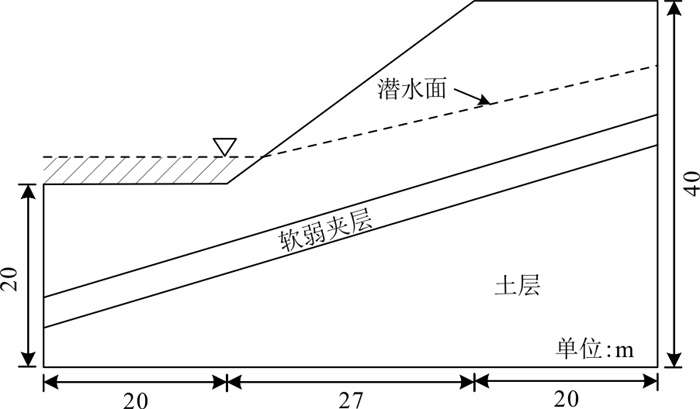
为验证轴对称模型对复杂边坡的适用性, 选取了澳大利亚计算机应用协会边坡分析中的第4考题, 如图 6所示, 该边坡由土层和软弱夹层组成, 其相应土体参数如表 2所示, 边坡中存在地下水并在坡脚处产生地表水, 地表水面高出地面3 m, 地下水孔压及潜水面位置通过在FLAC3D流体计算模式(model configure fluid)下设置相应孔压边界条件计算得到[19-20], 将地表水的作用以法向应力施加在地面积水处单元体表面。该边坡采用传统简化Bishop法计算得到的安全系数为0.739。
表 2 边坡土体力学参数Table 2. Mechanical parameters of slope土体类型 ρ/(kg·m-3) E/MPa μ c/kPa φ/(°) 软弱夹层 1 850 20 0.4 10 10 土层 1 800/2 000 80 0.3 28.5/26.0 20.0/18.0 注:“/”前后分别为土层的天然参数和饱和参数 以不同计算方法计算的安全系数结果如表 3所示, 表中极限平衡法一列为文献[10]中计算得到的值,可以看出, 对于该复杂边坡算例, 三维模型计算的安全系数与本文所提出轴对称模型计算的安全系数差距极小, 仅为0.049, 而平面应变模型计算的安全系数与三维模型相差较大, 差距达0.298, 这说明本文的轴对称模型对于复杂边坡模型同样适用。此外, 对比结果表明, 对于圆形凹坡, 平面应变模型与极限平衡法都是基于平面应变假定对三维空间问题进行的简化, 故两者的安全系数计算结果最为接近, 并且这2种方法均没有考虑空间形状效应对边坡稳定性的影响, 所以计算的安全系数均小于三维模型的安全系数。
表 3 不同方法的安全系数计算结果Table 3. Safety factor obtained from different methods三维模型 轴对称模型 平面应变模型 极限平衡法[10] 0.988 0.939 0.69 0.739 2. 应用实例
2.1 文献对比
Sun等[21]通过对ABAQUS中强度折减法进行改进, 以改进后的折减方法研究了边坡不同坡面形态对边坡三维稳定性的影响, 并通过大量计算, 绘制了不同坡面形态的边坡安全系数速查表(文献[21]中Fig. 8), 根据式(2)中的无量纲参数λ以及坡角β值可查得不同形态边坡的三维安全系数。本研究分别取λ=0.2,1.0, 坡角β=30°,45°,75°, 坡面形态为圆形的边坡, 首先按边坡参数查安全系数速查表得到其三维安全系数, 然后分别建立相应边坡的三维模型、轴对称模型和平面应变模型, 模型建立方法与前文所述方法完全一致, 计算得到相应边坡参数下的安全系数, 所得结果如表 4所示,可知对于所建立的各种边坡模型, 三维模型的安全系数计算结果与文献[21]中查表得到的考虑坡面形态的三维安全系数相差极小, 最小差值为0.01, 最大差值为0.1, 表明三维模型计算的安全系数较好地反映了圆形边坡的三维空间效应, 并且将本文所提出的轴对称模型计算的安全系数与文献[21]中的安全系数和三维模型的安全系数对比发现, 本文所提出的轴对称模型在减少了模型网格的情况下, 计算得到的安全系数与三维模型的计算结果相差无几, 最小差值为0.05, 最大差值为0.11, 计算结果更符合实际, 而平面应变模型计算的安全系数则与文献[21]的结果和三维模型的计算结果相差较大, 最大差值达到0.78, 过于保守, 这与文献[22]中的结论相符。
表 4 安全系数计算结果对比Table 4. Comparison of safety factorλ 坡角β/ (°) 文献[21] 结果 三维模型 轴对称模型 平面应变模型 0.2 30 1.91 1.97 1.87 1.60 45 1.58 1.57 1.50 1.25 75 1.08 1.14 1.04 0.81 1.0 30 2.38 2.37 2.26 1.60 45 2.06 2.02 1.95 1.55 75 1.51 1.61 1.56 1.21 2.2 工程应用
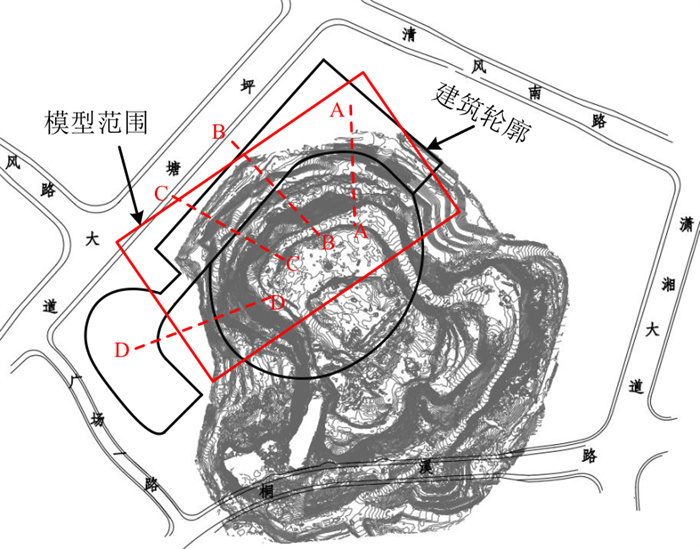
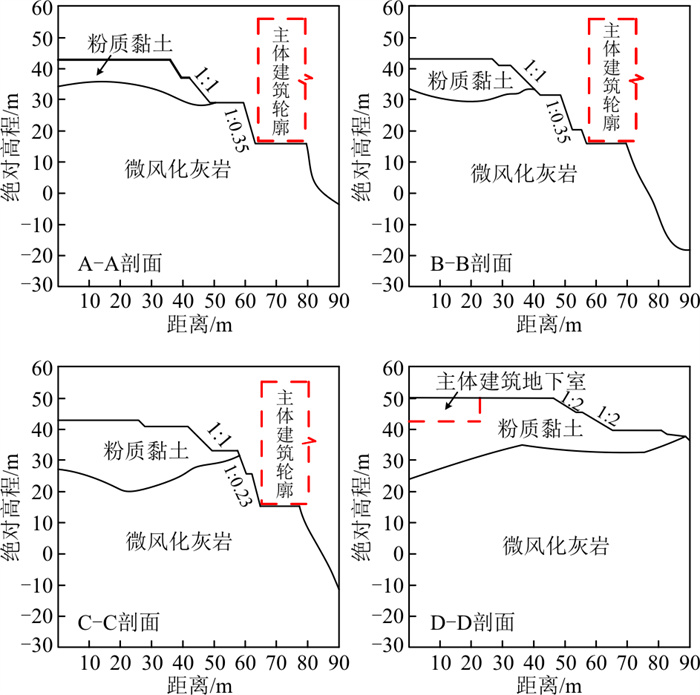
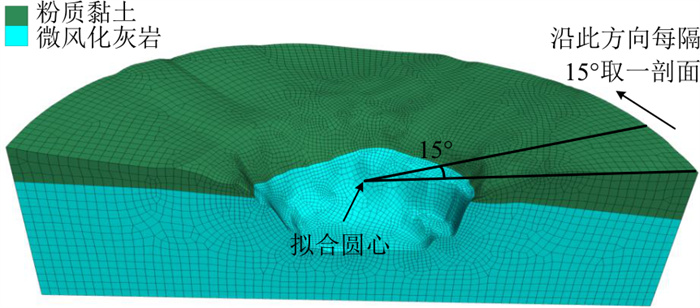
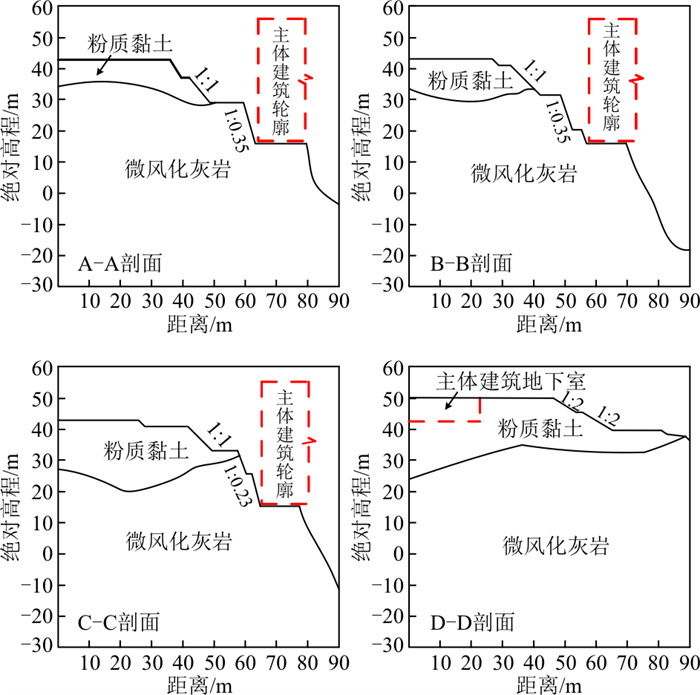
进一步将所提出的简化计算方法(轴对称模型)应用于长沙冰雪世界矿坑边坡加固工程, 所选取矿坑为经人工采石而成的似圆形岩质矿坑, 直径约180 m。坑壁边坡坡度一般在70°以上, 高度在70 m以上, 最高处有近100 m, 该矿坑所在区域地形平面图如图 7所示。根据勘察报告[23]结果, 该矿坑所在地区经历了槽、台、洼三大构造演化阶段, 现已进入余动期。至燕山晚期, 区域上整体处于缓慢间歇性抬升, 缺失古近系地层, 长期的侵蚀、剥蚀, 在近场地形成了不同级别的剥夷面和低丘岗地, 第四纪构造运动以差异性升降运动为主, 在场地内形成了多级阶地。边坡岩体大部分为古生界中泥盆统棋梓桥组浅灰色薄层至厚层灰岩, 基岩裸露, 表面见裂隙性溶蚀风化现象, 风化裂隙较发育, 岩体完整性受结构面溶蚀风化影响明显, 岩体强度有明显下降。坑壁顶部为较薄的红褐色人工填土和褐黄、褐灰色粉质黏土夹砾石, 其中A-A、B-B、C-C和D-D的地质剖面图如图 8所示。在工程修建前, 需对矿坑边坡进行削坡加固设计, 以保证后续项目的安全运营。根据岩土勘察报告[23]及相关岩体力学试验, 综合得到边坡岩土体的力学参数如表 5所示, 由于人工填土对边坡稳定性影响不大, 为简化计算, 后续稳定性评价中不考虑该地层。
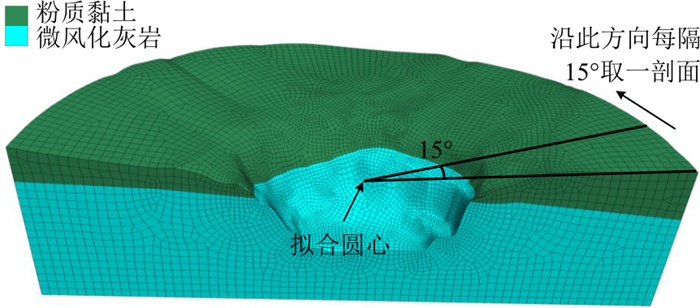
表 5 长沙冰雪世界项目边坡岩土体力学参数Table 5. Mechanical parameters of the slope in Changsha Ice World土体类型 ρ/(kg∙m-3) E/GPa μ c/kPa φ/(°) 粉质黏土 1 800 1.0 0.22 50 19 微风化灰岩 2 400 6 0.32 280 27 计算该矿坑边坡安全系数时, 先采用本文方法, 从模型左侧边界开始, 每隔15°取一剖面, 建立轴对称模型, 同时为对比计算, 建立相应剖面的平面应变模型和整体矿坑的三维模型并计算其安全系数。对于近似圆形矿坑边坡, 其轴对称模型的建立方法为:先基于整体的坡面形态, 拟合出最符合坡面形态的圆形, 以该圆的圆心向外引两条射线, 以两条射线间所切割形成的楔形建立最终轴对称模型。3种模型的边界约束条件与前文所述一致。
2.2.1 削坡处理前稳定性分析
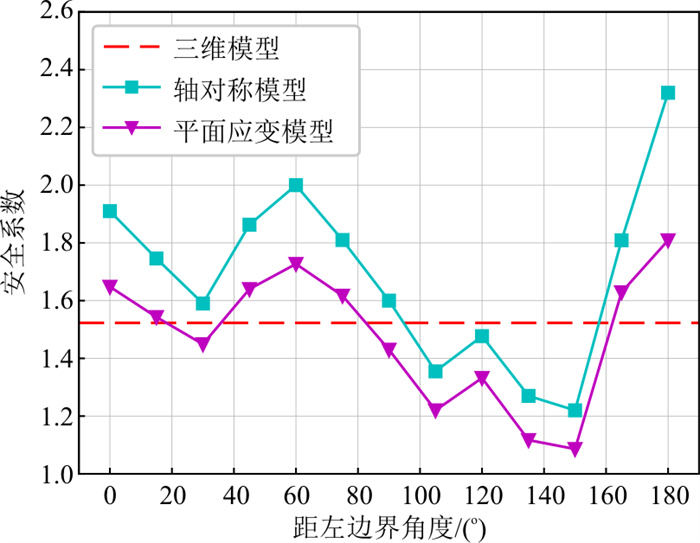
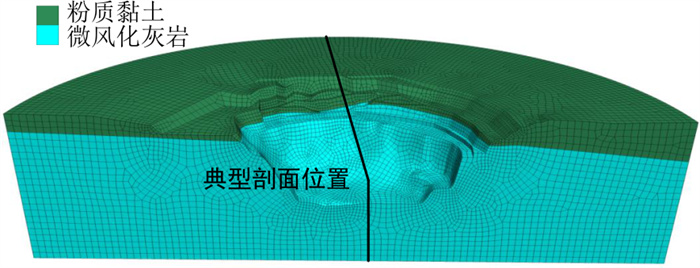
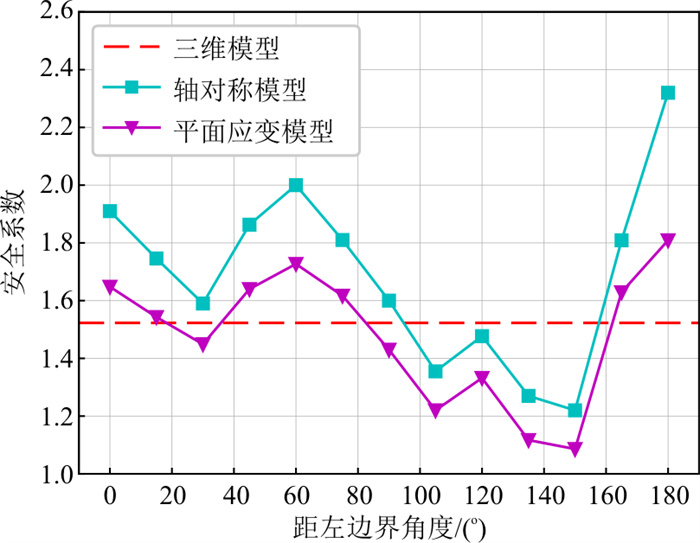
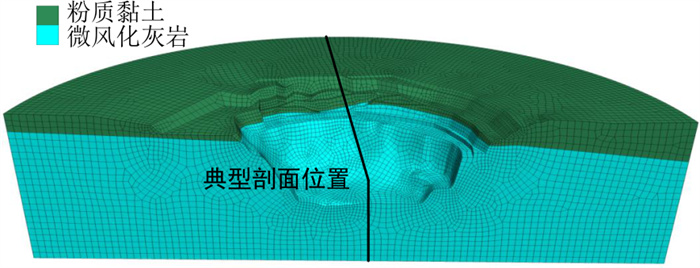
该矿坑边坡在削坡处理前的三维模型以及各剖面的位置如图 9所示, 分别计算三维模型和各剖面轴对称模型、平面应变模型的安全系数, 其中, 三维模型的安全系数由图 9所示的模型直接计算得到, 由于真实的边坡坡面形态及岩土体性质的差异, 故三维模型计算得到的安全系数为该边坡整体最小的安全系数, 该值仅表现出坡面中某一部分的稳定性, 本研究只作一参考值, 而在三维模型中取不同剖面计算二维安全系数时, 各剖面的坡面形态就因剖面位置的不同而不同, 相应计算得到的安全系数也不同。将3种模型的计算结果绘制成曲线, 如图 10所示, 可以看出, 该矿坑边坡的整体安全系数为1.53左右, 并结合各剖面的安全系数可得知, 最危险的剖面位于与模型左侧边界夹角为150°左右处, 以轴对称模型计算得该剖面的安全系数为1.21左右, 以平面应变模型计算得该剖面的安全系数为1.08左右, 表明该剖面附近极易发生失稳, 故需对该矿坑边坡进行削坡加固。
2.2.2 削坡处理后稳定性分析
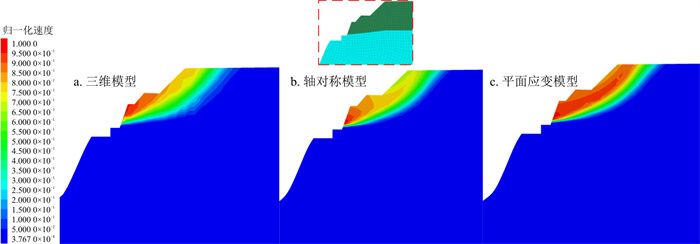
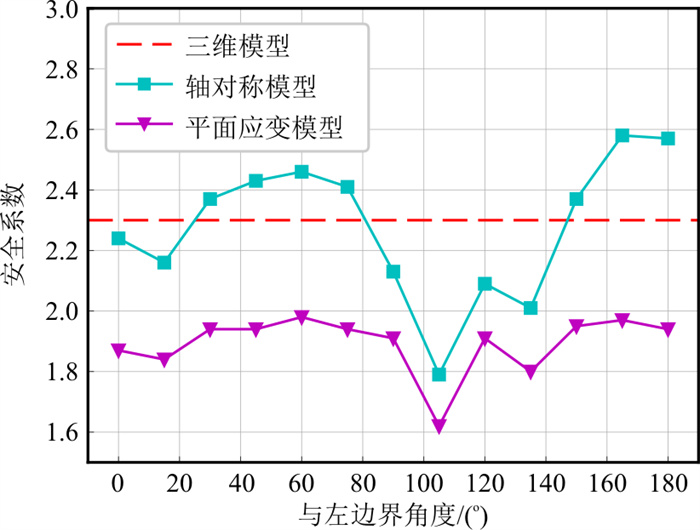
由前文计算得知该边坡在原始状态下稳定性较差, 容易失稳, 需对原始边坡进行削坡处理, 主要是针对上层软弱粉质黏土及部分岩体进行削坡处理, 削坡方案按照地质剖面图进行, 如图 11所示, 以原始地面及主体建筑标高为准, 采用分级放坡形式, 每级边坡顶部有2 m宽度的马道, 马道竖向距离一般不超过10 m, 土质边坡坡率一般为1∶2至1∶1, 岩质边坡可至1∶0.5左右, 坡面(含马道)均采用网喷混凝土进行防护, 削坡后的整体边坡模型如图 12所示。分别计算矿坑边坡三维模型的安全系数和各剖面轴对称模型、平面应变模型的安全系数, 如图 13所示, 可知经过削坡处理后, 边坡的整体安全系数从削坡前的1.53提高到2.3左右, 安全储备增加。各剖面的安全系数均有所提高, 削坡后的最危险剖面位于与模型左侧边界夹角为105°左右处, 其中以平面应变模型计算的安全系数较为保守, 安全系数仅1.61左右, 轴对称模型计算的安全系数较大, 在1.8左右, 这是由于传统平面应变模型的二维简化方式对于这种三维空间效应显著的边坡不太适用的原因, 而轴对称模型计算的安全系数考虑了边坡的三维空间效应, 这一点从该剖面的归一化速度云图(图 14)也可以看出, 轴对称模型的速度变化趋势与三维模型极为相似, 即速度最大值出现在坡脚处, 坡体内部的滑动是由坡脚滑动带动的, 相对而言, 平面应变模型的速度变化趋势与三维模型则相差较大, 表现为坡体内大部分区域滑动速度相同, 这与圆形凹坡的滑动方式不符[15]。
3. 结论
(1) 对于简单圆形均质凹坡, 通过改变坡角及土体参数对比计算, 所建立的轴对称模型计算的安全系数相比于传统以平面应变问题简化计算的安全系数更加准确;对于复杂程度各异的边坡类型, 通过对比计算发现, 本文所提出的轴对称模型建立方法同样适用。
(2) 以本文方法建立的轴对称模型计算边坡安全系数时, 结果要比真实值稍偏大, 而以传统平面应变模型计算的安全系数比真实值偏小, 趋于保守。在边坡加固设计时, 过于保守的安全系数会导致材料成本的增加。
(3) 将本文方法计算的安全系数与现有文献[21]对比, 两者结果相差不大, 表明本文方法不仅计算得到的安全系数准确, 而且能减少计算时间。
(4) 在类似工程中按照本文方法建立典型剖面的简化计算模型进行边坡稳定性评价, 在一定程度上提高了计算效率, 并且本文方法基于强度折减法, 相比于极限平衡法, 完全满足岩土体的应力应变本构关系, 更符合实际情况, 能满足快速辅助边坡加固设计的需求。
(5) 本文方法对近似圆形的矿坑边坡有较好的适用性, 但若边坡曲率变化很大, 则该方法后续还要进一步考虑边坡曲率对计算结果的影响, 需结合具体工程深入研究。
-
表 1 土体力学参数表
Table 1. Mechanical parameters of soil
密度ρ/ (kg∙m-3) 弹性模量E/GPa 泊松比μ 黏聚力c/kPa 内摩擦角φ/(°) 2 400 4.3 0.2 28 27 表 2 边坡土体力学参数
Table 2. Mechanical parameters of slope
土体类型 ρ/(kg·m-3) E/MPa μ c/kPa φ/(°) 软弱夹层 1 850 20 0.4 10 10 土层 1 800/2 000 80 0.3 28.5/26.0 20.0/18.0 注:“/”前后分别为土层的天然参数和饱和参数 表 3 不同方法的安全系数计算结果
Table 3. Safety factor obtained from different methods
三维模型 轴对称模型 平面应变模型 极限平衡法[10] 0.988 0.939 0.69 0.739 表 4 安全系数计算结果对比
Table 4. Comparison of safety factor
λ 坡角β/ (°) 文献[21] 结果 三维模型 轴对称模型 平面应变模型 0.2 30 1.91 1.97 1.87 1.60 45 1.58 1.57 1.50 1.25 75 1.08 1.14 1.04 0.81 1.0 30 2.38 2.37 2.26 1.60 45 2.06 2.02 1.95 1.55 75 1.51 1.61 1.56 1.21 表 5 长沙冰雪世界项目边坡岩土体力学参数
Table 5. Mechanical parameters of the slope in Changsha Ice World
土体类型 ρ/(kg∙m-3) E/GPa μ c/kPa φ/(°) 粉质黏土 1 800 1.0 0.22 50 19 微风化灰岩 2 400 6 0.32 280 27 -
[1] 彭柏兴, 王会云, 王小平, 等. 长沙冰雪世界高陡边坡工程地质特征及其稳定性评价[J]. 城市勘测, 2021(5): 181-187. https://www.cnki.com.cn/Article/CJFDTOTAL-CSKC202105045.htmPeng B X, Wang H Y, Wang X P, et al. Engineering geological characteristics and stability evaluation of high and steep slopes in Changsha Ice World[J]. Urban Geotechnical Investigation & Surveying, 2021(5): 181-187(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-CSKC202105045.htm [2] 肖锐铧, 王思敬, 贺小黑, 等. 非均质边坡多级稳定性分析方法[J]. 岩土工程学报, 2013, 35(6): 1062-1068. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201306012.htmXiao R H, Wang S J, He X H, et al. Multi-level stability analysis of inhomogeneous slopes[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(6): 1062-1068(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201306012.htm [3] 吴益平, 卢里尔, 薛阳. 基于临界状态的边坡渐进破坏力学模型分析及应用[J]. 地质科技通报, 2020, 39(5): 1-7. doi: 10.19509/j.cnki.dzkq.2020.0501Wu Y P, Lu L R, Xue Y. Application of landside progressive failure mechanical model based on the stress state[J]. Bulletin of Geological Science and Technology, 2020, 39(5): 1-7(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0501 [4] 赵尚毅, 郑颖人, 时卫民, 等. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报, 2002, 24(3): 343-346. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200203016.htmZhao S Y, Zheng Y R, Shi W M, et al. Analysis on safety factor of slope by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 343-346(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200203016.htm [5] 周珂, 黄小城, 雷德阳, 等. 平面剪切岩质边坡滑裂面的确定及稳定性分析[J]. 地质科技通报, 2022, 41(2): 325-334. doi: 10.19509/j.cnki.dzkq.2022.0062Zhou K, Huang X C, Lei D Y, et al. Determinations of the critical sliding surface of planar sliding rock slopes and their stability analysis[J]. Bulletin of Geological Science and Technology, 2022, 41(2): 325-334(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2022.0062 [6] Michalowski R L. Stability charts for uniform slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(4): 351-355. http://www.researchgate.net/profile/Radoslaw_Michalowski/publication/245293997_Stability_Charts_for_Uniform_Slopes/links/567ea4fe08aebccc4e05d233.pdf [7] 连镇营, 韩国城, 孔宪京. 强度折减有限元法研究开挖边坡的稳定性[J]. 岩土工程学报, 2001, 23(4): 407-411. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200104004.htmLian Z Y, Han G C, Kong X J. Stability analysis of excavation by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4): 407-411(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200104004.htm [8] 张雪娅, 秦庆词, 张雪娇. MIDAS三维数值软件在深凹露天边坡稳定性评价中的应用[J]. 化工矿物与加工, 2019, 48(7): 56-59. https://www.cnki.com.cn/Article/CJFDTOTAL-HGKJ201907015.htmZhang X Y, Qin Q C, Zhang X J. Application of MIDAS three-dimensional numerical software in stability evaluation of deep concave slope[J]. Industrial Minerals & Processing, 2019, 48(7): 56-59(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-HGKJ201907015.htm [9] 王龙. 非饱和土边坡三维稳定性极限分析研究[D]. 上海: 上海大学, 2019.Wang L. Limit analysis of three-dimensional stability of unsaturated soil slopes[D]. Shanghai: Shanghai University, 2019(in Chinese with English abstract). [10] 徐文刚, 余旭荣, 年廷凯, 等. 基于FLAC3D的三维边坡稳定性强度折减法计算效率改进算法及其应用[J]. 吉林大学学报: 地球科学版, 2021, 51(5): 1347-1355. https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ202105007.htmXu W G, Yu X R, Nian T K, et al. Optimization and application of FLAC3D strength-reduction computation in three-dimension slope stability analysis[J]. Journal of Jilin University: Earth Science Edition, 2021, 51(5): 1347-1355(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ202105007.htm [11] 徐芝纶. 弹性力学简明教程[M]. 北京: 高等教育出版社, 1980.Xu Z L. A concise course in elasticity[M]. Beijing: Higher Education Press, 1980(in Chinese). [12] 孙朝燚, 陈从新, 郑允, 等. 基于空间效应的弃渣场边坡稳定性方法探讨[J]. 西南交通大学学报, 2019, 54(1): 97-105. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201901013.htmSun C Y, Chen C X, Zheng Y, et al. Discussion on slope stability analysis method of abandoned dreg site based on spatial effect[J]. Journal of Southwest Jiaotong University, 2019, 54(1): 97-105(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201901013.htm [13] Baker R, Leshchinsky D. Stability analysis of conical heaps[J]. Doshitsu Kögakkai Ronbun Hökokushuü, 1987, 27(4): 99-110. http://ci.nii.ac.jp/naid/110003985196/en [14] 王家臣, 杜竞中. 水平凸型边坡破坏分析[J]. 中国矿业大学学报, 1992, 21(2): 105-111. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD199202013.htmWang J C, Du J Z. The failure analysis of horizontal convex earth slopes[J]. Journal of China University of Mining & Technology, 1992, 21(2): 105-111(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD199202013.htm [15] 赵衡, 宋二祥. 圆形凸坡的稳定性分析[J]. 岩土工程学报, 2011, 33(5): 730-737. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201105015.htmZhao H, Song E X. Stability analysis of circular convex slopes[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(5): 730-737(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201105015.htm [16] 卢坤林, 朱大勇. 坡面形态对边坡稳定性影响的理论与试验研究[J]. 岩石力学与工程学报, 2014, 33(1): 35-42. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201401004.htmLu K L, Zhu D Y. Theoretical and experimental study of effect of slope topography on its stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(1): 35-42(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201401004.htm [17] 赵尚毅, 郑颖人, 张玉芳. 有限元强度折减法中边坡失稳的判据探讨[J]. 岩土力学, 2005, 26(2): 332-336. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX20050200Y.htmZhao S Y, Zheng Y R, Zhang Y F. Study on slope failure criterion in strength reduction finite element method[J]. Rock and Soil Mechanics, 2005, 26(2): 332-336(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX20050200Y.htm [18] 张鲁渝, 郑颖人, 赵尚毅, 等. 有限元强度折减系数法计算土坡稳定安全系数的精度研究[J]. 水利学报, 2003, 34(1): 21-27. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200301004.htmZhang L Y, Zheng Y R, Zhao S Y, et al. The feasibility study of strength-reduction method with FEM for calculating safety factors of soil slope stability[J]. Journal of Hydraulic Engineering, 2003, 34(1): 21-27(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200301004.htm [19] 肖景红, 王敏, 王川, 等. 含优势渗流层边坡降雨入渗下的可靠度分析[J]. 地质科技通报, 2021, 40(6): 193-204. doi: 10.19509/j.cnki.dzkq.2021.0619Xiao J H, Wang M, Wang C. Reliability analysis of slope with dominant seepage interlayer under rainfall infiltration[J]. Bulletin of Geology Science and Technology, 2021, 40(6): 193-204(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2021.0619 [20] 曾江波, 付智勇, 肖林超, 等. 基于降雨作用下滑面抗剪强度动态变化的层状边坡稳定性评价[J]. 地质科技情报, 2018, 37(4): 225-231. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201804031.htmZeng J B, Fu Z Y, Xiao L C, et al. Slope stability evaluation considering variation of shear strength of slip surface in layered slope under rainfall[J]. Geological Science and Technology Information, 2018, 37(4): 225-231(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201804031.htm [21] Sun C W, Chai J R, Xu Z G, et al. 3D stability charts for convex and concave slopes in plan view with homogeneous soil based on the strength-reduction method[J]. International Journal of Geomechanics, 2017, 17(5): 06016034. [22] Cheng Y M, Liu H T, Wei W B, et al. Location of critical three-dimensional non-spherical failure surface by NURBS functions and ellipsoid with applications to highway slopes[J]. Computers and Geotechnics, 2005, 32(6): 387-399. http://www.onacademic.com/detail/journal_1000034063069210_a3fc.html [23] 长沙市规划勘测设计研究院. 长沙冰雪世界项目岩土工程详细勘察报告[R]. 长沙: 长沙市规划勘测设计研究院, 2014.Changsha Planning & Design Survey Research Institute. Geotechnical engineering detailed investigation report of Changsha Ice World[R]. Changsha: Changsha Planning & Design Survey Research Institute, 2014(in Chinese). 期刊类型引用(1)
1. 马明强. 废弃矿坑修复过程中边坡稳定性研究. 世界有色金属. 2025(01): 136-138 .  百度学术
百度学术其他类型引用(0)
-






 下载:
下载:














 下载:
下载:




 百度学术
百度学术