Research on audio-frequency magnetotelluric detection capability of geothermal clay cap based on trans-dimensional Bayesian inversion
-
摘要:
在地热探测中, 黏土盖层作为水热型地热系统的典型标志, 其埋藏深度及分布范围可为圈定地热资源的范围及确定地热钻井位置提供重要依据。黏土盖层通常由水热作用所形成的黏土层所构成, 表现为低阻特征, 利用音频大地电磁法可以对低阻盖层有效成像。为了获得黏土盖层位置分布及成像结果的不确定性信息, 采用一维变维度贝叶斯反演方法, 利用音频大地电磁数据对地热区低阻盖层的探测能力进行研究。首先进行模型试验, 建立一个典型地热系统的地电模型, 利用一维变维度贝叶斯算法对合成数据进行反演, 获得地下电性结构和界面位置不确定性信息。接着将其应用于山西阳高地热区一条实测音频大地电磁数据处理。模型试验发现该方法对低阻黏土盖层具有较为准确的识别能力, 所获得的低阻盖层上、下界面不确定分析的结果也较为可靠。实测数据试验发现, 该方法对浅层低阻盖层具有较好的识别能力, 并可以给出盖层界面位置的不确定性评价。该测线的二维非线性共轭梯度反演结果验证了一维贝叶斯反演的可靠性。该方法对浅层地热黏土盖层具有较准确的成像能力和不确定性分析能力, 在地热探测中具有较强的应用前景。
Abstract:Objective In geothermal exploration, a clay cap is a typical hydrothermal geothermal system, and its depth and distribution range can provide crucial information for delineating the scope of geothermal resources and determining the location of geothermal drilling. Clay caps are usually composed of a clay layer formed through hydrothermal reactions and are characterized by low resistance. The low-resistivity cap can be effectively imaged using the audio-frequency magnetotelluric method. To obtain uncertainty information about the distribution of clay cap layers and imaging results, this paper employs the 1D trans-dimensional Bayesian inversion method to investigate the detection capabilities of low-resistance cap layers in geothermal areas through audio electromagnetic data.
Methods In this paper, a model test is first carried out to establish a geoelectric model of a typical geothermal system.Subsequently, a 1D trans-dimensional Bayesian algorithm is used to invert the synthetic data to obtain the uncertainty information of the subsurface electrical structure and interface position. Then, the method was applied to the processing of measured audio frequency magnetotelluric data in the Yanggao geothermal area of Shanxi Province.
Results This method has relatively accurate identification ability for low-resistivity clay caps, and the obtained uncertainty analysis results of the upper and lower interfaces of low-resistivity caps are also relatively reliable according to numerical tests. It was found that this method has a good ability to identify shallow low-resistivity caps and can provide an uncertainty evaluation of the clay cap interface position via field data tests. The 2D inversion results of this survey line verify the reliability of the 1D inversion.
Conclusion This method has relatively accurate imaging capabilities and uncertainty analysis capabilities for shallow geothermal clay caprocks and has strong application prospects in geothermal detection.
-
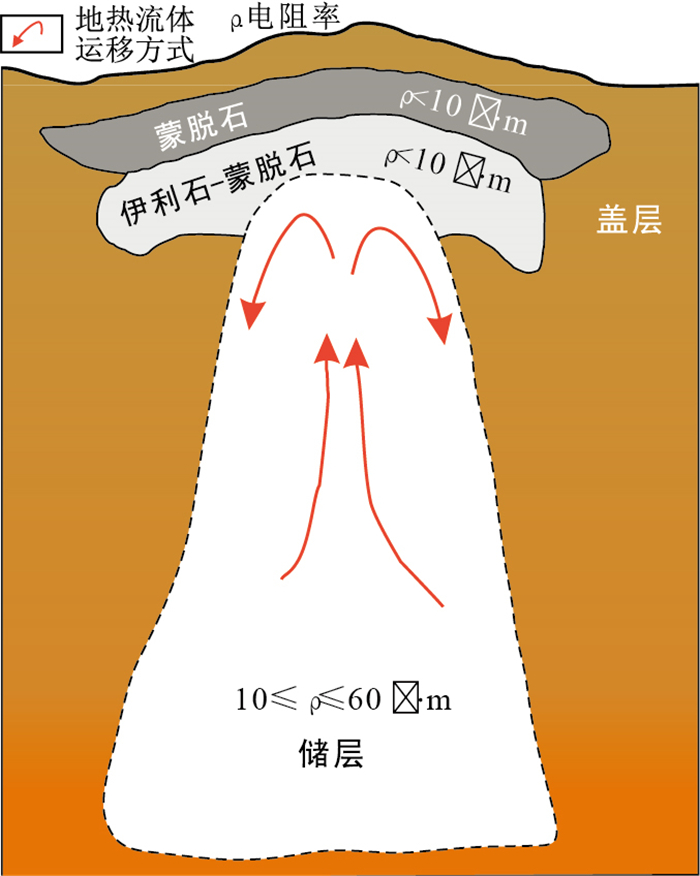
图 1 对流型水热系统概念图(据文献[34]修改)
Figure 1. Conceptual diagram of a convective hydrothermal system
图 3 地热地电模型测点布置图
Figure 3. Position of measuring point for geothermal geoelectric model
图 4 L4测线贝叶斯反演电阻率-深度后验概率分布图
Figure 4. Bayesian inversion resistivity-depth posterior probability distribution map of L4 measuring line
图 5 L4测线均值电阻率拟二维剖面图
Figure 5. Proposed-two-dimensional profile of mean resistivity of L4 measuring line
图 6 L4测线界面位置概率拟二维剖面
Figure 6. Proposed-two-dimensional profile of interface position probability of L4 measuing line
图 9 实测数据一维贝叶斯反演电阻率-深度后验概率分布图
Figure 9. 1D Bayesian inversion resistivity-depth posterior probability distribution map of measured data
-
[1] 曾昭发, 陈雄, 李静, 等. 地热地球物理勘探新进展[J]. 地球物理学进展, 2012, 27(1): 168-178. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201201020.htmZENG Z F, CHEN X, LI J, et al. Advancement of geothermal geophysics exploration[J]. Progress in Geophysics, 2012, 27(1): 168-178. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201201020.htm [2] ZHOU W L, HU X Y, GUO H D, et al. Three-dimensional magnetotelluric inversion reveals the typical geothermal structure of Yanggao geothermal field in Datong Basin, northern China[J]. Geothermics, 2022, 105: 102505. doi: 10.1016/j.geothermics.2022.102505 [3] 孙明行, 张起钻, 刘德民, 等. 广西干热型地热资源成因机制与赋存模式[J]. 地质科技通报, 2022, 41(3): 330-340. doi: 10.19509/j.cnki.dzkq.2022.0037SUN M H, ZHANG Q Z, LIU D M, et al. Genesis and occurrence models of hot-dry geothermal resources in Guangxi[J]. Bulletin of Geological Science and Technology, 2022, 41(3): 330-340. (in Chinese with English abstract) doi: 10.19509/j.cnki.dzkq.2022.0037 [4] 孟甲, 秦鹏, 史启朋, 等. 断陷盆地碳酸盐岩热储勘查及研究: 以鱼台凹陷为例[J]. 地质科技通报, 2022, 41(4): 38-45. doi: 10.19509/j.cnki.dzkq.2022.0035MENG J, QIN P, SHI Q P, et al. Exploration and study on carbonate thermal reservoirs in fault basins: A case from Yutai Sag[J]. Bulletin of Geological Science and Technology, 2022, 41(4): 38-45. (in Chinese with English abstract) doi: 10.19509/j.cnki.dzkq.2022.0035 [5] HAN Q, KELBERT A, HU X Y. An electrical conductivity model of a coastal geothermal field in southeastern China based on 3D magnetotelluric imaging[J]. Geophysics, 2021, 86(4): B265-B276. doi: 10.1190/geo2019-0446.1 [6] HE L F, CHEN L, DOR J I, et al. Mapping the geothermal system using AMT and MT in the Mapamyum (QP) field, Lake Manasarovar, southwestern Tibet[J]. Energies, 2016, 9(10): 855. doi: 10.3390/en9100855 [7] CHENG Y Z, PANG Z H, DI Q Y, et al. Three-dimensional resistivity structure in the hydrothermal system beneath Ganzi Basin, eastern margin of Tibetan Plateau[J]. Geothermics, 2021, 93: 102062. doi: 10.1016/j.geothermics.2021.102062 [8] CHENG Y Z, PANG Z H, KONG Y L, et al. Imaging the heat source of the Kangding high-temperature geothermal system on the Xianshuihe fault by magnetotelluric survey[J]. Geothermics, 2022, 102: 102386. doi: 10.1016/j.geothermics.2022.102386 [9] HEISE W, CALDWELL T G, BIBBY H M, et al. Three-dimensional modelling of magnetotelluric data from the Rotokawa geothermal field, Taupo Volcanic Zone, New Zealand[J]. Geophysical Journal International, 2008, 173(2): 740-750. doi: 10.1111/j.1365-246X.2008.03737.x [10] CONSTABLE S, KEY K, LEWIS L. Mapping offshore sedimentary structure using electromagnetic methods and terrain effects in marine magnetotelluric data[J]. Geophysical Journal International, 2009, 176(2): 431-442. doi: 10.1111/j.1365-246X.2008.03975.x [11] ROBERTSON K, THIEL S, MEQBEL N. Quality over quantity: On workflow and model space exploration of 3D inversion of MT data[J]. Earth, Planets and Space, 2020, 72(1): 2. doi: 10.1186/s40623-019-1125-4 [12] CONSTABLE S C, PARKER R L, CONSTABLE C G. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300. doi: 10.1190/1.1442303 [13] AUKEN E, CHRISTIANSEN A V. Layered and laterally constrained 2D inversion of resistivity data[J]. Geophysics, 2004, 69(3): 752-761. doi: 10.1190/1.1759461 [14] TARANTOLA A. Inverse problem theory and methods for model parameter estimation[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2005. [15] CHEN J S, KEMNA A, HUBBARD S S. A comparison between Gauss-Newton and Markov-chain Monte Carlo-based methods for inverting spectral induced-polarization data for Cole-Cole parameters[J]. Geophysics, 2008, 73(6): F247-F259. doi: 10.1190/1.2976115 [16] 尹彬, 胡祥云. 非线性反演的贝叶斯方法研究综述[J]. 地球物理学进展, 2016, 31(3): 1027-1032. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201603012.htmYIN B, HU X Y. Overview of nonlinear inversion using Bayesian method[J]. Progress in Geophysics, 2016, 31(3): 1027-1032. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ201603012.htm [17] GUO R W, DOSSO S E, LIU J X, et al. Frequency- and spatial-correlated noise on layered magnetotelluric inversion[J]. Geophysical Journal International, 2014, 199(2): 1205-1213. doi: 10.1093/gji/ggu329 [18] MANDOLESI E, OGAYA X, CAMPANYÀ J, et al. A reversible-jump Markov chain Monte Carlo algorithm for 1D inversion of magnetotelluric data[J]. Computers & Geosciences, 2018, 113: 94-105. [19] XIANG E M, GUO R W, DOSSO S E, et al. Efficient hierarchical trans-dimensional Bayesian inversion of magnetotelluric data[J]. Geophysical Journal International, 2018, 213(3): 1751-1767. doi: 10.1093/gji/ggy071 [20] BLATTER D, KEY K, RAY A, et al. Bayesian joint inversion of controlled source electromagnetic and magnetotelluric data to image freshwater aquifer offshore New Jersey[J]. Geophysical Journal International, 2019, 218(3): 1822-1837. doi: 10.1093/gji/ggz253 [21] PENG R H, HAN B, LIU Y J, et al. A Julia software package for transdimensional Bayesian inversion of electromagnetic data over horizontally stratified media[J]. Geophysics, 2022, 87(5): F55-F66. doi: 10.1190/geo2021-0534.1 [22] CONWAY D, SIMPSON J, DIDANA Y, et al. Probabilistic magnetotelluric inversion with adaptive regularisation using the No-U-turns sampler[J]. Pure and Applied Geophysics, 2018, 175(8): 2881-2894. doi: 10.1007/s00024-018-1870-5 [23] CHEN J S, HOVERSTEN G M, KEY K, et al. Stochastic inversion of magnetotelluric data using a sharp boundary parameterization and application to a geothermal site[J]. Geophysics, 2012, 77(4): E265-E279. doi: 10.1190/geo2011-0430.1 [24] 周思杰, 黄清华. 基于贝叶斯方法的二维大地电磁尖锐边界反演研究[J]. 地球物理学报, 2018, 61(8): 3420-3434. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201808027.htmZHOU S J, HUANG Q H. Two-dimensional sharp boundary magnetotelluric inversion using Bayesian theory[J]. Chinese Journal of Geophysics, 2018, 61(8): 3420-3434. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201808027.htm [25] BLATTER D, RAY A, KEY K. Two-dimensional Bayesian inversion of magnetotelluric data using trans-dimensional Gaussian processes[J]. Geophysical Journal International, 2021, 226(1): 548-563. doi: 10.1093/gji/ggab110 [26] 王贵玲, 蔺文静. 我国主要水热型地热系统形成机制与成因模式[J]. 地质学报, 2020, 94(7): 1923-1937. doi: 10.3969/j.issn.0001-5717.2020.07.002WANG G L, LIN W J. Main hydro-geothermal systems and their genetic models in China[J]. Acta Geologica Sinica, 2020, 94(7): 1923-1937. (in Chinese with English abstract) doi: 10.3969/j.issn.0001-5717.2020.07.002 [27] ARDID A, DEMPSEY D, BERTRAND E, et al. Bayesian magnetotelluric inversion using methylene blue structural priors for imaging shallow conductors in geothermal fields[J]. Geophysics, 2021, 86(3): E171-E183. doi: 10.1190/geo2020-0226.1 [28] MALINVERNO A. Parsimonious Bayesian Markov chain Monte Carlo inversion in a nonlinear geophysical problem[J]. Geophysical Journal International, 2002, 151(3): 675-688. doi: 10.1046/j.1365-246X.2002.01847.x [29] MINSLEY B J. A trans-dimensional Bayesian Markov chain Monte Carlo algorithm for model assessment using frequency-domain electromagnetic data[J]. Geophysical Journal International, 2011, 187(1): 252-272. doi: 10.1111/j.1365-246X.2011.05165.x [30] METROPOLIS N, ROSENBLUTH A W, ROSENBLUTH M N, et al. Equation of state calculations by fast computing machines[J]. Journal of Chemical Physics, 1953, 21(6): 1087-1092. doi: 10.1063/1.1699114 [31] HASTINGS W K. Monte Carlo sampling methods using Markov chains and their applications[J]. Biometrika, 1970, 57(1): 97-109. doi: 10.1093/biomet/57.1.97 [32] GREEN P J. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination[J]. Biometrika, 1995, 82(4): 711-732. doi: 10.1093/biomet/82.4.711 [33] AGOSTINETTI N P, MALINVERNO A. Receiver function inversion by trans-dimensional Monte Carlo sampling[J]. Geophysical Journal International, 2010, 181(2): 858-872. [34] PELLERIN L, JOHNSTON J M, HOHMANN G W. A numerical evaluation of electromagnetic methods in geothermal exploration[J]. Geophysics, 1996, 61(1): 121-130. doi: 10.1190/1.1443931 [35] KELBERT A, MEQBEL N, EGBERT G D, et al. ModEM: A modular system for inversion of electromagnetic geophysical data[J]. Computers & Geosciences, 2014, 66: 40-53. [36] 杨建中. 阳高县平山村P1地热井地热资源评价[J]. 山西建筑, 2014, 40(20): 238-240. https://www.cnki.com.cn/Article/CJFDTOTAL-JZSX201420126.htmYANG J Z. Geothermal resource evaluation of P1 geothermal well in Pingshan Village, Yanggao County[J]. Shanxi Architecture, 2014, 40(20): 238-240. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-JZSX201420126.htm -
下载:
点击查看大图
计量
- 文章访问数: 205
- PDF下载量: 45
- 被引次数: 0
