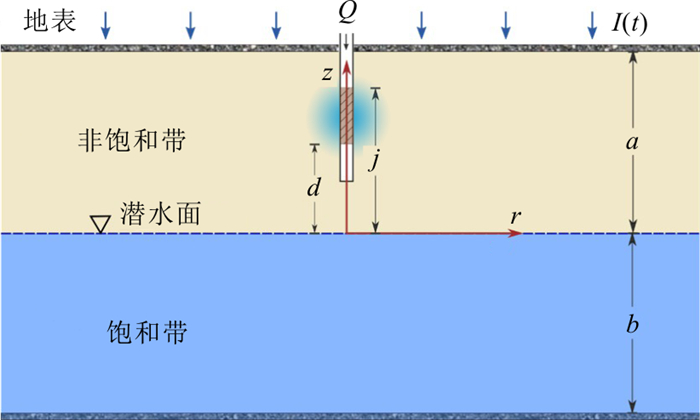
Analysis of unsaturated-saturated flow induced by a vadose zone well injection
-
摘要:
包气带井回灌是人工补给含水层的重要方法。在回灌过程中，非饱和带水力参数的准确描述对于提高评价精度、增强回灌管理具有重要意义。目前已有的许多包气带井回灌的解析模型是基于Gardner土壤水分特征曲线模型(含二参数)建立的，随着三参数模型(MB模型)和四参数模型(MN模型)的提出，一个值得关注的问题是使用更加灵活的土壤水分特征曲线模型是否能提高回灌系统中非饱和-饱和流的模拟精度。本研究采用MN模型(Gardner模型和MB模型为其子集)建立了包气带井回灌模型，使用COMSOL Multiphysics对模型进行求解，所得解用于研究在回灌过程中非饱和带水力参数和地表通量对非饱和-饱和流的影响，并比较在回灌过程中基于不同土壤水分特征曲线模型所得到的水力响应。试验结果分析发现包气带井回灌引起的水力响应以及地表通量对回灌的影响均会受到非饱和带渗透性以及储水能力的影响，相对渗透系数指数
ω k影响非饱和带渗透系数的变化，持水指数ω c影响非饱和带的储水能力，将指数参数简化为ω k=ω c=ω 会在计算和预测包气带井回灌引起的水力响应时带来一定的误差。压力头阈值差b 1=ψ a-ψ k的绝对值较小时，对水头增量的影响也较小，此时将其简化为b 1=ψ a-ψ k=0所带来的误差也较小。本研究成果可以帮助学者们提高对包气带井回灌过程的认识，对于回灌方案设计、实施和管理具有重要的实际意义。-
关键词:
- 包气带井 /
- 人工回灌 /
- 非饱和-饱和流 /
- 土壤水分特征曲线模型
Abstract:Objective Vadose zone well (VZW) injection is an effective method of managed aquifer recharge (MAR). To improve VZW injection management, it is of great importance to accurately describe the unsaturated zone properties. Several analytical models have been developed for VZW injection based on the two-parameter constitutive model (Gardner model). As the three-parameter model (MB model) and four-parameter model (MN model) have been proposed, it is of interest to know whether the application of more flexible constitutive models is able to improve the analysis of unsaturated-saturated flow induced by VZW injection.
Methods In this study, the MN model (which includes the Gardner model and MB model as subsets) was employed to establish a VZW injection model. The model was solved using COMSOL Multiphysics. The results are utilized to investigate the unsaturated-saturated flow induced by VZW injection for different values of the unsaturated zone properties to analyse the influences of the ground surface flux (GSF), and to compare the hydraulic responses based on different exponential constitutive models.
Results The analysis demonstrates that the hydraulic response induced by VZW injection and the influence of ground surface flux are affected by the hydraulic conductivity and the water storage capacity of the unsaturated zone. The relative hydraulic conductivity exponent
ω k affects the change in hydraulic conductivity of the unsaturated zone. The moisture retention exponentω c affects the water storage capacity of the unsaturated zone. The approximation ofω k=ω c=ω will result in some errors in the calculation and prediction of the hydraulic response caused by VZW injection. When the absolute value difference of the pressure head thresholdb 1=ψ a-ψ k is small, its effect on the water head increment is small. In this case, it is reasonable to assume thatb 1=ψ a-ψ k=0.Conclusion This study can help scholars improve the understanding of the VZW injection process and has important practical significance for the design, implementation and management of injection schemes.
-
图 1 包气带井回灌以及地表通量所引起的非饱和-饱和流示意图
a为非饱和带厚度；b为饱和带厚度；d为回灌井段底部到初始地下水的垂直距离；I(t)为地表通量；Q为流量；r为沿水平径向水流方向的坐轴标；j为回灌井段顶部到初始地下水位的垂直距离
Figure 1. Schematic diagrams of unsaturated-saturated flow induced by vadose zone well injection and ground surface flux
图 2 包气带井回灌的二维轴对称数值模型示意
bD为无量纲饱和带厚度；dD为底部到初始地下水位的垂直距离；jD为回灌井段顶部到初始地下水位的无量纲垂直距离
Figure 2. Geometry of the 2D axisymmetric numerical model
图 3 不同无量纲相对渗透系数指数ωDk对应的无量纲水头增量uD和sD随tD的变化(a)以及$\frac{\partial u_{\mathrm{D}}}{\partial t_{\mathrm{D}}} $和$\frac{\partial s_{\mathrm{D}}}{\partial t_{\mathrm{D}}} $随tD的变化(b)
非饱和带取样点rD=0.1, zD=0.1，参数ωDc=1, b1D=ψDa-ψDk=0；饱和带取样点rD=0.1, zD=-0.1，参数ωDc=1, b1D=ψDa-ψDk=0。图中虚线代表基于Gardner模型所求得的不同ωD对应的解
Figure 3. For different values of the dimensionless relative hydraulic conductivity exponent ωDk: the dimensionless hydraulic head increments uD and sD vs. the dimensionless time tD (a); $\frac{\partial u_{\mathrm{D}}}{\partial t_{\mathrm{D}}} $ and $\frac{\partial s_{\mathrm{D}}}{\partial t_{\mathrm{D}}} $ vs. tD (b)
图 4 不同无量纲持水指数ωDc对应的无量纲水头增量uD和sD随tD的变化(a)以及$\frac{\partial u_{\mathrm{D}}}{\partial t_{\mathrm{D}}} $和$\frac{\partial s_{\mathrm{D}}}{\partial t_{\mathrm{D}}} $随tD的变化(b)
非饱和带取样点rD=0.1, zD=0.1，参数ωDk=3, b1D=ψDa-ψDk=0；饱和带取样点rD=0.1, zD=-0.1，参数ωDk=3, b1D=ψDa-ψDk=0。图中虚线代表基于Gardner模型所求得的不同ωD对应的解
Figure 4. For different values of the dimensionless moisture retention exponent ωDc: the dimensionless hydraulic head increments uD and sD vs. the dimensionless time tD (a); $\frac{\partial u_{\mathrm{D}}}{\partial t_{\mathrm{D}}} $ and $\frac{\partial s_{\mathrm{D}}}{\partial t_{\mathrm{D}}} $ vs. tD (b)
图 5 不同b1D=ψDa-ψDk对应的无量纲水头增量uD(a)和sD(b)随tD的变化
a.取样点rD=0.1, zD=0.1, 参数ωDk=3, ωDc=1; b.取样点rD=0.1, zD=-0.1, 参数ωDk=3, ωDc=1
Figure 5. Dimensionless hydraulic head increments uD (a) and sD(b) vs. the dimensionless time tD for different values of b1D=ψDa-ψDk
图 6 在tD∈[200, 250)期间施加ID=1时，不同无量纲相对渗透系数指数ωDk对应的时间无量纲水头增量uD(a)和sD(b)随tD的变化
a.取样点rD=0.1, zD=0.1，参数ωDc=3, b1D=ψDa-ψDk=0；b.取样点rD=0.1, zD=-0.1，参数ωDc=3, b1D=ψDa-ψDk=0。图中虚线代表施加相同ID情况下基于Gardner模型所求得的不同ωD对应的解
Figure 6. For different values of the dimensionless relative hydraulic conductivity exponent ωDk: The dimensionless hydraulic head increments uD (a) and sD (b) vs. the dimensionless time tD with ID=1 during tD∈[200, 250)
图 7 在tD∈[200, 250)期间施加ID=1时，不同无量纲持水指数ωDc对应的无量纲水头增量uD(a)和sD(b)随tD的变化
a.取样点rD=0.1, zD=0.1，参数ωDk=0.5, b1D=ψDa-ψDk=0；b.取样点rD=0.1, zD=-0.1，参数ωDk=0.5, b1D=ψDa-ψDk=0。图中虚线代表施加相同ID情况下基于Gardner模型所求得的不同ωD对应的解
Figure 7. For different values of the dimensionless relative hydraulic conductivity exponent ωDk: The dimensionless hydraulic head increments uD (a) and sD (b) vs. the dimensionless time tD with ID=1 during tD∈[200, 250)
图 8 在tD∈[200, 250)期间不同b1D=ψDa-ψDk对应的无量纲水头增量uD(a)和sD (b)随tD的变化
a.取样点rD=0.1, zD=0.1，参数ωDk=1, ωDc=3；b.取样点rD=0.1, zD=-0.1，参数ωDk=1, ωDc=3;实线为施加ID=1的情况，虚线为不施加ID的情况
Figure 8. Dimensionless hydraulic head increments uD (a) and sD (b) vs. the dimensionless time tD for b1D=ψDa-ψDk with ID=1 during tD∈[200, 250) (solid curves) and without ID (dotted curves)
-
[1] Sprenger C, Hartog N, Hernández M, et al. Inventory of managed aquifer recharge sites in Europe: Historical development, current situation and perspectives[J]. Hydrogeology Journal, 2017, 25(6): 1909-1922. doi: 10.1007/s10040-017-1554-8 [2] Ghayoumian J, Saravi M M, Feiznia S, et al. Application of GIS techniques to determine areas most suitable for artificial groundwater recharge in a coastal aquifer in southern Iran[J]. Journal of Asian Earth Sciences, 2007, 30(2): 364-374. doi: 10.1016/j.jseaes.2006.11.002 [3] Karlsen R H, Smits F, Stuyfzand P, et al. A post audit and inverse modeling in reactive transport: 50 years of artificial recharge in the Amsterdam Water Supply Dunes[J]. Journal of Hydrology, 2012, 454: 7-25. [4] Lacher L, Turner D, Gungle B, et al. Application of hydrologic tools and monitoring to support managed aquifer recharge decision making in the upper San Pedro River, Arizona, USA[J]. Water, 2014, 6(11): 3495-3527. doi: 10.3390/w6113495 [5] Kuster M, Díaz-Cruz S, Rosell M, et al. Fate of selected pesticides, estrogens, progestogens and volatile organic compounds during artificial aquifer recharge using surface waters[J]. Chemosphere, 2010, 79(8): 880-886. doi: 10.1016/j.chemosphere.2010.02.026 [6] Sharma S K, Kennedy M D. Soil aquifer treatment for wastewater treatment and reuse[J]. International Biodeterioration & Biodegradation, 2017, 119(S1): 671-677. [7] 杜新强, 王钰升, 冶雪艳, 等, 大清河流域平原区地下水人工补给潜力与补给方式分析[J]. 吉林大学学报: 地球科学版, 2022, 52(2): 535-549. https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ202202016.htmDu X Q, Wang Y S, Ye X Y, et al. Artificial aquifer recharge potential and methods in plain area of Daqing river basin[J]. Journal of Jilin University: Earth Science Edition, 2022, 52(2): 535-549(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ202202016.htm [8] García-Menéndez O, Ballesteros B J, Renau-Pruñonosa A, et al. Using electrical resistivity tomography to assess the effectiveness of managed aquifer recharge in a salinized coastal aquifer[J]. Environmental Monitoring and Assessment, 2018, 190(2): 1-19. [9] Shammas M I. The effectiveness of artificial recharge in combating seawater intrusion in Salalah coastal aquifer, Oman[J]. Environmental Geology, 2008, 55(1): 191-204. doi: 10.1007/s00254-007-0975-4 [10] Shi X, Jiang S, Xu H, et al. The effects of artificial recharge of groundwater on controlling land subsidence and its influence on groundwater quality and aquifer energy storage in Shanghai, China[J]. Environmental Earth Sciences, 2016, 75(3): 1-18. [11] Bouwer H. Artificial recharge of groundwater: Hydrogeology and engineering[J]. Hydrogeology Journal, 2002, 10(1): 121-142. doi: 10.1007/s10040-001-0182-4 [12] Dillon P. Future management of aquifer recharge[J]. Hydrogeology Journal, 2005, 13(1): 313-326. doi: 10.1007/s10040-004-0413-6 [13] Dillon P, Toze S, Page D, et al. Managed aquifer recharge: Rediscovering nature as a leading edge technology[J]. Water Science and Technology, 2010, 62(10): 2338-2345. doi: 10.2166/wst.2010.444 [14] 张学真. 地下水人工补给研究现状与前瞻[J]. 地下水, 2005, 27(1): 25-28, 66. doi: 10.3969/j.issn.1004-1184.2005.01.011Zhang X Z. Research situation and prospective of artificial groundwater recharge[J]. Ground Water, 2005, 27(1): 25-28, 66(in Chinese with English abstract). doi: 10.3969/j.issn.1004-1184.2005.01.011 [15] 郭华明, 王焰新, 王润福, 等, 人类活动影响下的大同市浅层地下水环境演化[J]. 地质科技情报, 2002, 21(4): 65-72. doi: 10.3969/j.issn.1000-7849.2002.04.014Guo H M, Wang Y X, Wang R F, et al. Environmental evolution of shallow groundwater in Datong City under the influence of human activities[J]. Geological Science and Technology Information, 2002, 21(4): 65-72(in Chinese with English abstract). doi: 10.3969/j.issn.1000-7849.2002.04.014 [16] 韩鹏飞, 王旭升, 张俊, 等. 近50 a来新疆孔雀河灌区地下水流系统演变特征[J]. 地质科技通报, 2022, 41(1): 109-118. doi: 10.19509/j.cnki.dzkq.2022.0023Han P F, Wang X S, Zhang J, et al. Evolution characteristics of groundwater flow systems in the past 50 years in Kongqi River irrigation district, Xinjiang, China[J]. Bulletin of Geological Science and Technology, 2022, 41(1): 109-118(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2022.0023 [17] Heilweil V M, Benoit J, Healy R W. Variably saturated groundwater modelling for optimizing managed aquifer recharge using trench infiltration[J]. Hydrological Processes, 2015, 29(13): 3010-3019. doi: 10.1002/hyp.10413 [18] Bouwer H, Pyne R, Brown J, et al. Design, operation and maintenance for sustainable underground storage facilities[R]. Denver: Report, American Water Works Association Research Foundation, Denver, CO, 2008. [19] Jansen H, Stenstrom M, De Koning J. Development of indirect potable reuse in impacted areas of the United States[J]. Water Science and Technology, 2007, 55(1/2): 357-366. [20] Liu G, Knobbe S, Reboulet E C, et al. Field investigation of a new recharge approach for ASR projects in near-surface aquifers[J]. Groundwater, 2016, 54(3): 425-433. doi: 10.1111/gwat.12363 [21] Lluria M. Successful application of managed aquifer recharge in the improvement of the water resources management of semi-arid regions: Examples from Arizona and the Southwestern USA[J]. Boletín Geológicoy Minero, 2009, 120(2): 111-120. [22] Hao Q, Shao J, Cui Y, et al. Applicability of artificial recharge of groundwater in the Yongding River alluvial fan in Beijing through numerical simulation[J]. Journal of Earth Science, 2014, 25(3): 575-586. doi: 10.1007/s12583-014-0442-6 [23] Wang W, Sun X, Xu Y. Recent advances in managed aquifer recharge in China[C]//Anon. Proceedings of the 2010 International Conference on Challenges in Environmental Science and Computer Engineering, F, 2010. [S. l.]: IEEE. [24] Händel F, Binder M, Dietze M, et al. Experimental recharge by small-diameter wells: The Pirna, Saxony, case study[J]. Environmental Earth Sciences, 2016, 75(10): 1-8. [25] Jokela P, Kallio E. Sprinkling and well infiltration in managed aquifer recharge for drinking water quality improvement in Finland[J]. Journal of Hydrologic Engineering, 2015, 20(3): B4014002. doi: 10.1061/(ASCE)HE.1943-5584.0000975 [26] San-Sebastián-Sauto J, Fernández-Escalante E, Calero-Gil R, et al. Characterization and benchmarking of seven managed aquifer recharge systems in south-western Europe[J]. Sustainable Water Resources Management, 2018, 4(2): 193-215. doi: 10.1007/s40899-018-0232-x [27] Moench A F. Importance of the vadose zone in analyses of unconfined aquifer tests[J]. Groundwater, 2004, 42(2): 223-233. doi: 10.1111/j.1745-6584.2004.tb02669.x [28] Nwankwor G, Cherry J, Gillham R. A comparative study of specific yield determinations for a shallow sand aquifer[J]. Groundwater, 1984, 22(6): 764-772. doi: 10.1111/j.1745-6584.1984.tb01445.x [29] Nwankwor G, Gillham R, Van Der Kamp G, et al. Unsaturated and saturated flow in response to pumping of an unconfined aquifer: Field evidence of delayed drainage[J]. Groundwater, 1992, 30(5): 690-700. doi: 10.1111/j.1745-6584.1992.tb01555.x [30] Kool J, Parker J, Van Genuchten M T. Determining soil hydraulic properties from one-step outflow experiments by parameter estimation: I. Theory and numerical studies[J]. Soil Science Society of America Journal, 1985, 49(6): 1348-1354. doi: 10.2136/sssaj1985.03615995004900060004x [31] Zachmann D, Duchateau P, Klute A. Simultaneous approximation of water capacity and soil hydraulic conductivity by parameter identification1[J]. Soil Science, 1982, 134(3): 157-163. doi: 10.1097/00010694-198209000-00002 [32] Zachmann D, Duchateau P, Klute A. The calibration of the richards flow equation for a draining column by parameter identification 1[J]. Soil Science Society of America Journal, 1981, 45(6): 1012-1015. doi: 10.2136/sssaj1981.03615995004500060002x [33] Russo D. Determining soil hydraulic properties by parameter estimation: On the selection of a model for the hydraulic properties[J]. Water Resources Research, 1988, 24(3): 453-459. doi: 10.1029/WR024i003p00453 [34] Gardner W. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table[J]. Soil Science, 1958, 85(4): 228-232. doi: 10.1097/00010694-195804000-00006 [35] Kroszynski U I, Dagan G. Well pumping in unconfined aquifers: The influence of the unsaturated zone[J]. Water Resources Research, 1975, 11(3): 479-490. doi: 10.1029/WR011i003p00479 [36] Chang C H, Huang C S, Yeh H D. Analysis of three-dimensional unsaturated-saturated flow induced by localized recharge in unconfined aquifers[J]. Hydrology and Earth System Sciences, 2018, 22(7): 3951-3963. doi: 10.5194/hess-22-3951-2018 [37] Liang X, Zhan H, Zhang Y K, et al. Base flow recession from unsaturated-saturated porous media considering lateral unsaturated discharge and aquifer compressibility[J]. Water Resources Research, 2017, 53(9): 7832-7852. doi: 10.1002/2017WR020938 [38] Lin Y C, Li M H, Yeh H D. An analytical model for flow induced by a constant-head pumping in a leaky unconfined aquifer system with considering unsaturated flow[J]. Advances in Water Resources, 2017, 107: 525-534. doi: 10.1016/j.advwatres.2017.05.018 [39] Tartakovsky G D, Neuman S P. Three-dimensional saturated-unsaturated flow with axial symmetry to a partially penetrating well in a compressible unconfined aquifer[J]. Water Resources Research, 2007, 43(1): W01410. [40] Moench A F. Analytical and numerical analyses of an unconfined aquifer test considering unsaturated zone characteristics[J]. Water Resources Research, 2008, 44(6): W06409. [41] Mathias S A, Butler A P. Linearized Richards' equation approach to pumping test analysis in compressible aquifers[J]. Water Resources Research, 2006, 42(6): W06408. [42] Mishra P K, Neuman S P. Improved forward and inverse analyses of saturated-unsaturated flow toward a well in a compressible unconfined aquifer[J]. Water Resources Research, 2010, 46(7): W07508. [43] Liang X, Zhan H, Zhang Y K. Aquiferrecharge using a vadose zone infiltration well[J]. Water Resources Research, 2018, 54(11): 8847-8863. doi: 10.1029/2018WR023409 [44] Qi C, Zhan H, Liang X, et al. Influence of time-dependent ground surface flux on aquifer recharge with a vadose zone injection well[J]. Journal of Hydrology, 2020, 584: 124739. doi: 10.1016/j.jhydrol.2020.124739 [45] Brooks R H, Corey A T. Properties of porous media affecting fluid flow[J]. Journal of the Irrigation and Drainage Division, 1966, 92(2): 61-90. doi: 10.1061/JRCEA4.0000425 [46] Mualem Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research, 1976, 12(3): 513-522. doi: 10.1029/WR012i003p00513 [47] Van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils 1[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. doi: 10.2136/sssaj1980.03615995004400050002x [48] 王大纯. 水文地质学基础[M]. 北京: 地质出版社, 1986.Wang D C. Fundamentals of hydrogeology[M]. Beijing: Geological Publishing House, 1986(in Chinese). [49] Philip J R. Theory of infiltration: Advances in hydroscience[M]. [S. l.]: Elsevier, 1969. [50] 陈刚, 陈爱娣, 杨杏玲. 再谈量纲分析法[J]. 物理通报, 2000(12): 6-8. https://www.cnki.com.cn/Article/CJFDTOTAL-WLTB200012003.htmChen G, Chen A D, Yang X L. Talking about dimensional analysis[J]. Physics Bulletin, 2000(12): 6-8(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-WLTB200012003.htm [51] Maliska C R. On the physical significance of some dimensionless numbers used in heat transfer and fluid flow[J]. Federal University of Santa Catarina, Florianópolis, SC, 1990, 137: 1-12. [52] Moench A F. Transient flow to a large-diameter well in an aquifer with storative semiconfining layers[J]. Water Resources Research, 1985, 21(8): 1121-1131. doi: 10.1029/WR021i008p01121 [53] Martin R. Clogging issues associated with managed aquifer recharge methods[M]. [S. l.]: IAH Commission on Managing Aquifer Recharge, Australia, 2013. [54] Xian Y, Jin M, Zhan H, et al. Reactive transport of nutrients and bioclogging during dynamic disconnection process of stream and groundwater[J]. Water Resources Research, 2019, 55(5): 3882-3903. doi: 10.1029/2019WR024826 [55] Zhang X Z, Huo A D, Wang J C. The comparative analysis of two injection modes and recharge capacity estimation for a radial well in the loess area of China[J]. Earth and Enovironmental Science, 2020, 467: 012059. [56] Jeong H Y, Jun S C, Cheon J Y, et al. A review on clogging mechanisms and managements in aquifer storage and recovery (ASR) applications[J]. Geosciences Journal, 2018, 22(4): 667-679. doi: 10.1007/s12303-017-0073-x -
下载:
点击查看大图
计量
- 文章访问数: 706
- PDF下载量: 43
- 被引次数: 0
