考虑河床渗透性影响的基流退水过程解析模型

摘要:
基流退水过程分析是流域尺度平均水文地质参数估计的有效方法之一, 但传统基流退水过程模型未考虑河床的渗透性, 其对参数估计的影响并不清楚。针对这个问题, 建立了降水入渗及河水位波动驱动下, 考虑河床渗透性影响的潜水含水层地下水流数学模型, 运用格林函数方法推导出水位及流量的解析解, 并利用数值模拟验证了解析解。结果表明, 在降水入渗强度波动的驱动下, 河床渗透性越小, 降水入渗引起更高的地下水位上升, 更低的基流量峰值, 更慢的基流退水过程; 河水位波动驱动下, 河床渗透性更低时, 地下水位对河水位波动的响应更弱, 地表水-地下水交互通量更小; 河床渗透性显著影响基流退水曲线, 退水早期, 低渗透性的河床导致曲线斜率远大于3, 而退水后期, 曲线斜率趋近于1, 且其不受河床渗透性影响。当河床渗透性较差时, 由于忽略了河床渗透性的影响, 传统模型会过高估计基流量, 过低估计含水层的渗透系数。
- 基流退水过程 /
- 含水层补给 /
- 河水位波动 /
- 河床渗透性 /
- 解析解
Abstract: Objective
Baseflow recession analysis is an effective approach to estimating watershed-scale hydrogeological parameters. However, the traditional baseflow recession model did not consider the effects of semipervious riverbanks, and their influence on parameter estimation is unclear.
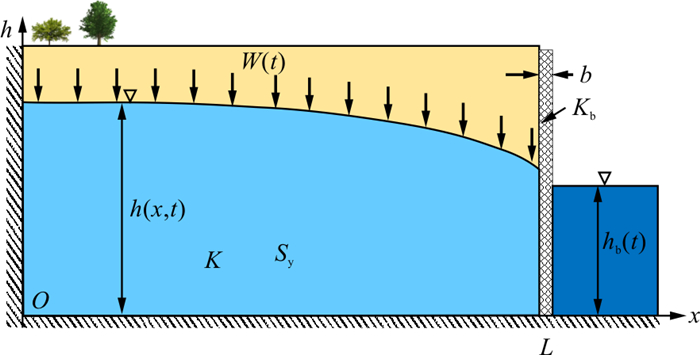
Methods
To address this issue, a mathematical model for groundwater flow in an unconfined aquifer with time-dependent recharge and river stages is presented. The effects of the semipervious riverbank are specifically taken into consideration. The analytical solutions of the hydraulic head and discharge are derived by using Green's function method, and their validities are tested by numerical simulations.
Results
The results show that, forced by the fluctuating recharge rate, the lower riverbank permeability leads to a higher peak of hydraulic heads, a lower baseflow, and slower baseflow recessions. For the case forced by the fluctuating river stages, the lower riverbank permeability leads to the weaker responses of water flow to the fluctuated river stage and the lower fluxes of surface water-groundwater interaction. The riverbank permeability significantly affects the baseflow recession curves. During early stage, the low riverbank permeability caused the power index of the recession curve to be larger than 3. For later stage, the power index approaches 1, which is not affected by the riverbank permeability.
Conclusion
For a low riverbank permeability, the traditional model will overestimate the baseflow and underestimate the hydraulic conductivities of aquifers because it neglects the effects of riverbank permeability.
- baseflow recession /
- aquifer recharge /
- river stage fluctuation /
- riverbank permeability /
- analytical solution
注释:

(所有作者声明不存在利益冲突)

HTML全文

图 1 潜水含水层剖面地下水流的概念模型

h(x, t)为地下水的水头；K为含水层渗透系数；W(t)为含水层随时间变化的补给率；S_y为给水度；K_b为河床渗透系数；b为河床厚度；h_b(t)为随时间波动的河床水位

Figure 1. Schematic diagram of groundwater flow in a cross-section of unconfined aquifers

下载: 全尺寸图片幻灯片

图 2 入渗补给波动下地下水位及基流的解析解和数值解对比

a.2次降水入渗补给事件；b.不同位置的地下水位；c.基流；W_D为降水入渗补给强度；h_D为河床水位；Q_D为基流量

Figure 2. Comparison of the analytical solution and the numerical solution for hydraulic heads and baseflow induced by time-varying recharge

下载: 全尺寸图片幻灯片

图 3 河水位波动下地下水位及基流解析解和数值解对比

a.河水位及不同位置地下水位；b.基流

Figure 3. Comparison of the analytical solution and the numerical solution for hydraulic heads and baseflow induced by time-varying river stages

下载: 全尺寸图片幻灯片

图 4 地下水位和基流在不同α影响下对补给波动的响应

a.2次降水入渗补给事件；b.x_D=0.5处地下水位；c.基流

Figure 4. Responses of hydraulic heads and baseflow induced by time-varying recharge

下载: 全尺寸图片幻灯片

图 5 x_D=0.5处地下水位和基流在不同α影响下对河水位波动的响应

a.河水位及不同α的地下水位；b.不同α的基流

Figure 5. Responses of hydraulic heads at x_D=0.5 and baseflow induced by time-varying river stages

下载: 全尺寸图片幻灯片

图 6 地下水位在不同α影响下对河水位波动的响应

a.α=0.1；b.α=1；c.α=10；d.无河床影响解

Figure 6. Responses of hydraulic heads induced by time-varying river stages for different α

下载: 全尺寸图片幻灯片

图 7 基流在W_D=0，h_bD=0.6时不同α影响下的变化

Figure 7. Change in baseflow with time for different α when W_D=0 and h_bD=0.6

下载: 全尺寸图片幻灯片

图 8 不同α的影响下-dQ_D/dt_D与Q_D的双对数坐标图

Figure 8. log-log plots for -dQ_D/dt_D vs. Q_D for different α

下载: 全尺寸图片幻灯片

图 9 不同α的退水曲线指数b随时间的变化

Figure 9. Changes in exponent b of the baseflow recession hydrograph with time at different α

下载: 全尺寸图片幻灯片

参考文献(20)

[1]	Fetter C W. Applied hydrogeology[M]. [S. l. ]: Waveland Press, 2018.
[2]	Freeze R A, Cherry J A. Groundwater[M]. [S. l. ]: Prentice Hall, 1979.
[3]	中国地质调查局. 水文地质手册[M]. 北京: 地质出版社, 2012. China Geological Survey. Handbook of hydrogeology[M]. Beijing: Geological Publishing House, 2012(in Chinese).
[4]	成建梅, 罗一鸣. 岩溶多重介质地下水模拟技术及应用进展[J]. 地质科技通报, 2022, 41(5): 220-229. doi: 10.19509/j.cnki.dzkq.2022.0220 Cheng J M, Luo Y M. Overview of groundwater modeling technology and its application in karst areas with multiple-void media[J]. Bulletin of Geological Science and Technology, 2022, 41(5): 220-229(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2022.0220
[5]	郑小康, 杨志兵. 岩溶含水层饱和-非饱和流动与污染物运移数值模拟[J]. 地质科技通报, 2022, 41(5): 357-366. doi: 10.19509/j.cnki.dzkq.2022.0211 Zheng X K, Yang Z B. Numerical simulation of saturated-unsaturated groundwater flow and contaminant transport in a karst aquifer[J]. Bulletin of Geological Science and Technology, 2022, 41(5): 357-366(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2022.0211
[6]	Liang X, Zhan H, Zhang Y K, et al. Base flow recession from unsaturated-saturated porous media considering lateral unsaturated discharge and aquifer compressibility[J]. Water Resources Research, 2017, 53(9): 7832-7852. doi: 10.1002/2017WR020938
[7]	Brutsaert W, Lopez J P. Basin-scale geohydrologic drought flow features of riparian aquifers in the southern Great Plains[J]. Water Resources Research, 1998, 34(2): 233-240. doi: 10.1029/97WR03068
[8]	Brutsaert W, Nieber J L. Regionalized drought flow hydrographs from a mature glaciated plateau[J]. Water Resources Research, 1977, 13(3): 637-643. doi: 10.1029/WR013i003p00637
[9]	徐磊磊, 刘敬林, 金昌杰, 等. 水文过程的基流分割方法研究进展[J]. 应用生态学报, 2011, 22(11): 3073-3080. https://www.cnki.com.cn/Article/CJFDTOTAL-YYSB201111041.htm Xu L L, Liu J L, Jin C J, et al. Baseflow separation methods in hydrological process research: A review[J]. Chinese Journal of Applied Ecology, 2011, 22(11): 3073-3080(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YYSB201111041.htm
[10]	Rupp D E, Selker J S. On the use of the Boussinesq equation for interpreting recession hydrographs from sloping aquifers[J]. Water Resources Research, 2006, 42(12): W12421.
[11]	Boussinesq J. Recherches théoriques sur l'écoulement des nappes d'eau infiltrées dans le sol et sur le débit des sources[J]. Journal de Mathématiques Pures et Appliquées, 1904, 10: 5-78.
[12]	Polubarinova-Kochina P Y. Theory of ground water movement[M]. Princeton: Princeton University Press, 2015.
[13]	Boussinesq J. Sur le débit, en temps de sécheresse, d'une source alimentée par une nappe d'eaux d'infiltration[J]. CR Hebd. Seanc. Acad. Sci. Paris, 1903, 136: 1511-1517.
[14]	Troch P A, Berne A, Bogaart P, et al. The importance of hydraulic groundwater theory in catchment hydrology: The legacy of Wilfried Brutsaert and Jean-Yves Parlange[J]. Water Resources Research, 2013, 49(9): 5099-5116.
[15]	Rupp D E, Selker J S. Drainage of a horizontal Boussinesq aquifer with a power law hydraulic conductivity profile[J]. Water Resources Research, 2005, 41(11): W11422.
[16]	Hayek M. Accurate approximate semi-analytical solutions to the Boussinesq groundwater flow equation for recharging and discharging of horizontal unconfined aquifers[J]. Journal of Hydrology, 2019, 570: 411-422.
[17]	Xian Y, Jin M, Zhan H. Buffer effect on identifying transient streambed hydraulic conductivity with inversion of flood wave responses[J]. Journal of Hydrology, 2020, 580: 124261.
[18]	Liang X, Zhan H, Schilling K. Spatiotemporal responses of groundwater flow and aquifer-river exchanges to flood events[J]. Water Resources Research, 2018, 54(3): 1513-1532.
[19]	Liang X, Zhang Y K. A new analytical method for groundwater recharge and discharge estimation[J]. Journal of Hydrology, 2012, 450: 17-24.
[20]	Liang X, Zhang Y K. Analytic solutions to transient groundwater flow under time-dependent sources in a heterogeneous aquifer bounded by fluctuating river stage[J]. Advances in Water Resources, 2013, 58: 1-9.