尺度效应最初是在研究渗透系数和溶质运移弥散度的过程中发现的一种现象：渗透系数和弥散度的实验室测量值往往比野外实测值小好几个数量级，这种渗透系数等参数随着研究尺度的变化而变化的现象称为尺度效应^[1-2]。一般而言，空间上分布的参数在高度非均质的条件下都具有强烈的尺度效应。目前，国内外对渗透性尺度效应的研究手段主要分为物理试验法和数值试验法。孙蓉琳等^[3]在溪洛渡坝区的玄武岩区域进行了多组不同尺度的水文地质试验，发现大尺度试验下得到的玄武岩渗透系数比小尺度试验更大且数值分布更为集中。刘日成等^[4]基于UDEC平台进行二次开发，研究了裂隙网络模型的尺度效应并确定了典型单元体(REV)尺度。高超等^[5]基于COMSOL数值模拟软件研究了单裂隙渗透性的尺度效应，结果表明单裂隙的渗透性随试样尺寸增大而增大，达到某一临界值后稳定。

在裂隙介质渗流场模拟过程中，由于尺度效应的存在，当试验测量尺度显著小于模拟尺度时，试验测量尺度得到的渗透性参数值往往不能直接运用于模拟尺度。因此，升尺度方法被提出来用以解决渗透性参数尺度转换的问题，其目的在于将精细尺度(试验尺度)下的参数转换为粗尺度(模拟尺度)研究中的参数，并同时保持该参数场的有效性。升尺度方法通常包括统计平均法、体积平均法、均匀化理论和重整化技术，而根据对象的不同，又可分为参数升尺度和过程升尺度2种：参数升尺度指对于地下水中溶质的有效迁移和反应参数升尺度；过程升尺度指迁移方程升尺度^[6-9]。覃荣高等^[10]对升尺度转换问题进行系统综述，指出了升尺度转换在目前水文地质研究中主要解决的问题以及存在的问题。郭富欣等^[11]对不同升尺度方法运算前后的模型分别进行数值模拟，通过数值模拟结果对比进行了升尺度方法优选以确定最适合研究区的升尺度方法。

由于结晶岩裂隙介质往往具有高度的非均质性和空间随机性，且岩石基质自身渗透性较低，其渗透性的空间尺度效应表现得尤为显著^[12]。因此对结晶岩裂隙介质渗透性升尺度转换的研究，具有十分重要的意义。然而，针对参数升尺度，大部分学者提出的升尺度算法是针对非均质孔隙介质的，裂隙介质的升尺度算法少，且大多是基于一定的研究场地，算法非常复杂，并不具有普适性，而升尺度的目的正是避免繁琐的计算，所以这些算法对于大型工程项目的实用性比较有限^[13-15]。针对目前存在的一些问题和实际工程需求，本研究将应用普适性的升尺度方法对结晶岩裂隙介质渗透性的升尺度转换做更为详细的探讨。

笔者拟以某地下水封洞库工程为例，在前期高精度勘察工作的基础上分析研究区裂隙发育规律，采用Monte-Carlo方法建立研究区岩体二维离散裂隙网络模型。通过编译对应MATLAB程序分别计算不同尺寸模拟域的渗透性参数，研究其随模拟域尺寸的变化规律并分析渗透性REV尺寸，之后对裂隙网络模型进行不同尺寸网格化处理，计算各个网格单元的等效渗透系数，并采用3种普适性的升尺度方法对小于REV尺寸的网格单元的等效渗透系数进行运算，并将计算结果与裂隙网络模型计算得到的对应复合网格单元的等效渗透系数进行对比，从而为实际模型应用中渗流场模拟提供借鉴。

1.   研究区二维离散裂隙网络模型

1.1   研究区概况

研究区地下水封洞库工程建设场地位于山东省烟台市临港经济技术开发区内，在大地构造上处于华北断块区东部的胶辽断块之中，地层岩性划分成3个种类：①第四系冲洪积层(Qhl，Qhb，$ \text{Q}\hat{s}$)；②燕山早期中粗粒黑云二长花岗岩(γ₅²⁽¹⁾)；③煌斑岩脉、石英脉等各种岩脉。库区选址已避开周边主要断裂，但洞库建设区域内仍发育多条次级断裂，破碎带以及节理裂隙密集带。

1.2   二维离散裂隙网络模型生成

基于Monte-Carlo法对二维离散裂隙网络进行模拟的前提是单个裂隙能够用裂隙的产状、迹长、隙宽以及中心点坐标等几何参数完全表征，即在确认这些几何参数以后，可以在裂隙网络模型中完全刻画出这条裂隙的所有信息^[16-19]。

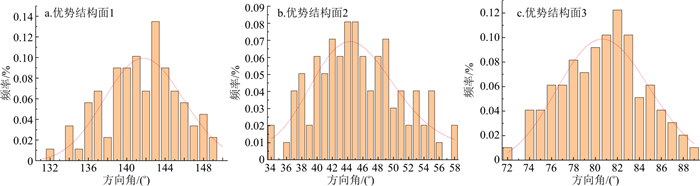
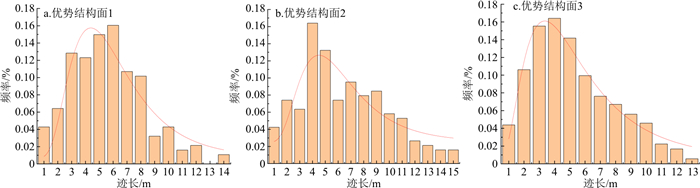
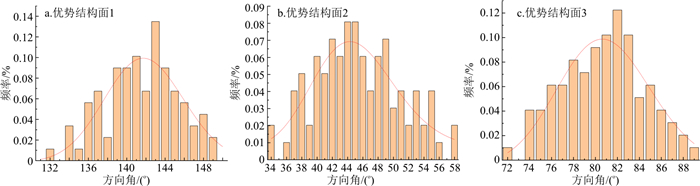
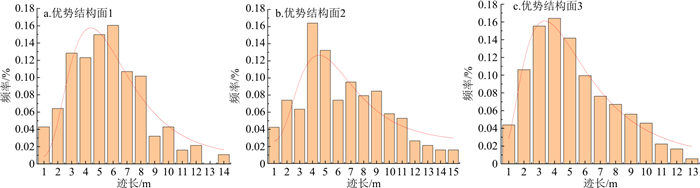
以研究区地下水封洞库的结晶岩裂隙介质统计数据为基础，主要是通过地表裂隙测量、水幕巷道地质素描图以及钻孔电视智能成像等数据资料对研究区内的裂隙几何特征参数进行统计和分析。研究区的地下裂隙岩体共发育3组较为明显的优势结构面，第1组裂隙结构面的倾向为NE0°~80°，倾角为30°~45°；第2组裂隙结构面的倾向为SE100°~140°，倾角为35°~50°；第3组裂隙结构面的倾向为NW290°~350°，倾角为70°~85°。3个优势裂隙组的裂隙方向角都近似服从正态分布(图 1)，迹长都近似服从对数正态分布(图 2)。由于岩体裂隙宽度大部分都在0.001 m以内，现有的技术手段都很难对这些裂隙宽度进行精确的测量，因此本研究参考前人给出的经验值，假定隙宽服从均值为0.000 4 m、标准差为0.0002 m的对数正态分布。3组裂隙的方向角、迹长、隙宽和密度的统计规律如表 1所示。此外，由于裂隙的分布具有高度的空间随机性，结合地质素描图中所观察到的裂隙发育情况，假设在二维裂隙网络模拟中，裂隙中心点的位置服从均匀分布。

图  1  优势结构面1，2，3方向角分布直方图

Figure  1.  Histogram of the angular distribution in directions 1, 2 and 3 of the dominant structural plane

下载: 全尺寸图片 幻灯片

图  2  优势结构面1，2，3迹长分布直方图

Figure  2.  Histogram of trace length distribution of dominant structural planes 1, 2 and 3

下载: 全尺寸图片 幻灯片

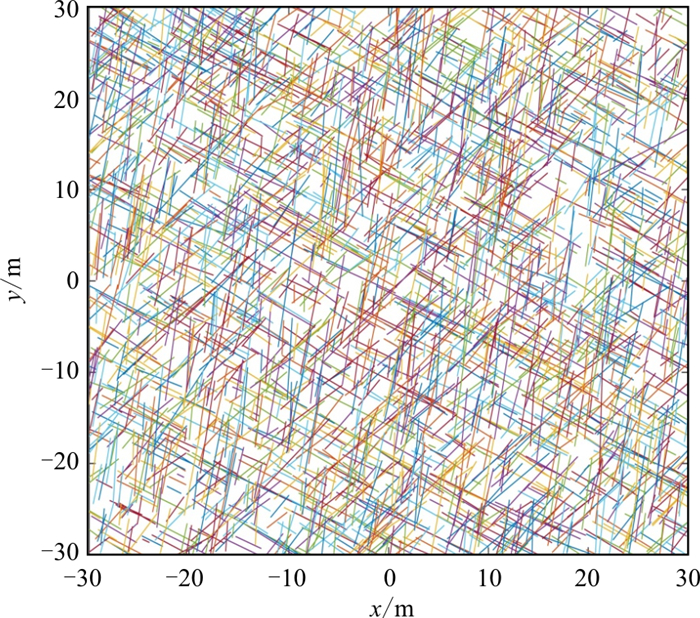
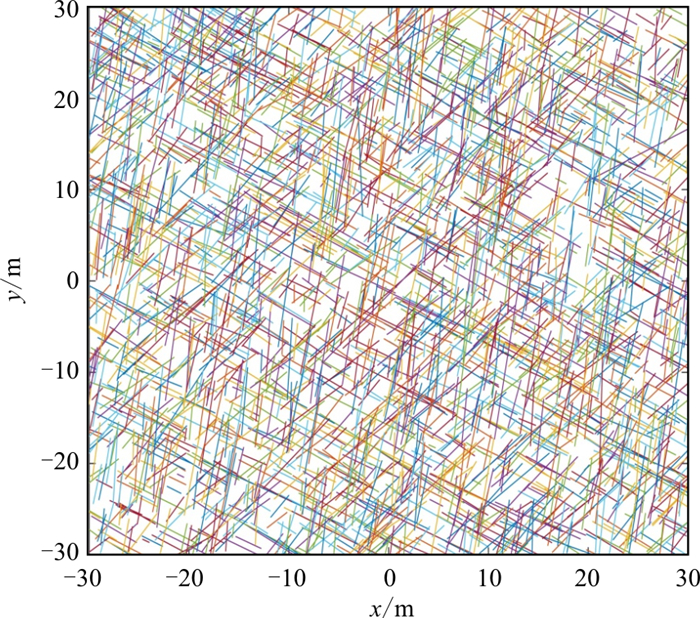
表  1  优势裂隙组各个几何参数分布类型及统计规律

Table  1.  Distribution types and statistical rules of geometric parameters in the dominant fracture group

优势裂隙组数	方向角(正态分布)			迹长(对数正态分布)			隙宽(对数正态分布)		密度/(条·m-2)
	均值/(°)	标准差/(°)		均值/m	标准差/m		均值/m	标准差/m
1	142.29	3.78		5.23	2.90		0.000 4	0.000 2	0.29
2	45.91	5.51		5.62	2.67		0.000 4	0.000 2	0.23
3	81.29	3.63		6.42	3.34		0.000 4	0.000 2	0.24

下载: 导出CSV 

| 显示表格

根据表 1中的迹长数据，迹长均值为5.23~6.42 m，为确保后续裂隙渗流计算数据稳定，确定裂隙生成域为60 m×60 m，计算域取30 m×30 m。在MATLAB环境中编写相应的程序，并将表 1中裂隙各个几何参数的概率分布模型参数代入，生成符合实际场地裂隙发育规律的二维裂隙网络模型，如图 3。其中第1组优势裂隙为1 044条，第2组优势裂隙为864条，第3组优势裂隙为828条，生成域内共2 736条裂隙，与表 1优势裂隙组密度分布情况一致。

图  3  基于烟台洞库数据的二维裂隙网络模型效果图

Figure  3.  Effect of the two-dimensional fracture network model based on Yantai cave data

下载: 全尺寸图片 幻灯片

2.   裂隙岩体渗透张量确定

离散裂隙网络渗流模型忽略了低渗透性的岩块孔隙系统，假定流体只在裂隙网络中运动，从而将裂隙岩体介质系统转化为裂隙网络介质系统。在左、右边界为存在水头差的定水头边界，水头值分别为15, 10 m，上下边界为隔水边界的条件下，本研究基于离散裂隙网络稳定渗流数学模型计算裂隙岩体渗透系数，并通过求解不同方向上的渗透系数来拟合渗透椭圆的方法，得到裂隙岩体的渗透张量。

左右定水头边界上的渗流量公式为：

式中: Q为渗流量；A₁，A₂，A₃为衔接矩阵，分别描述裂隙网络内节点、裂隙与上下边界交点和裂隙与左右边界交点与线单元的衔接关系；T为对角矩阵，该矩阵中对角线上的元素为$T_j=\frac{\rho g \lambda b_j^3}{\mu} \frac{h_j}{L_j} $，其中，ρ为裂隙密度，g为重力加速度，λ是与裂隙面粗糙程度相关的系数，本研究假设裂隙光直平滑，λ取1/12，b_j为第j条裂隙的隙宽，μ为地下水的动力黏滞系数；h_j为水头，L_j为渗透途径。H₁，H₂，H₃为水头矩阵，令渗流域内的裂隙网络内节点数为N₁，第二类边界点数量为N₂，第一类边界点数量为N₃，则H₁，H₂，H₃分别为N₁×1，N₂×1，N₃×1阶水头向量。

根据达西定律，沿着水头梯度方向上的渗透系数K可由下式求得：

式中：K为渗透系数；v为渗透流速；J为水力梯度；H₁、H₂为上下游过水断面的水头。

对于二维裂隙网络模型渗流分析问题，渗透张量K_ij是一个二阶对称张量。将结构面的渗透性平均到裂隙岩体中，得到均质各向异性的裂隙介质，K_ij为渗透张量，记作[K]。用矩阵可表示为：

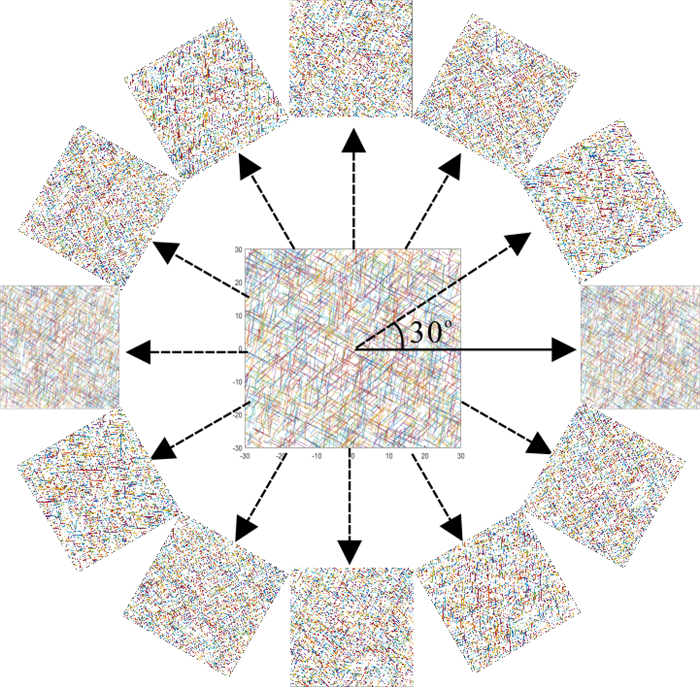
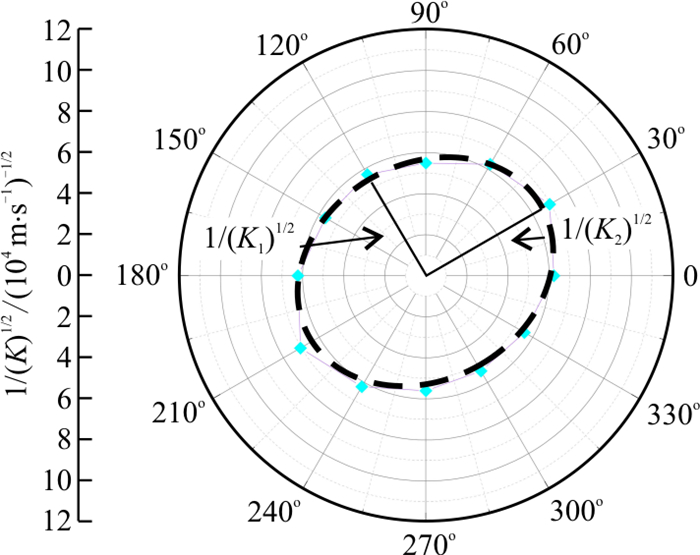
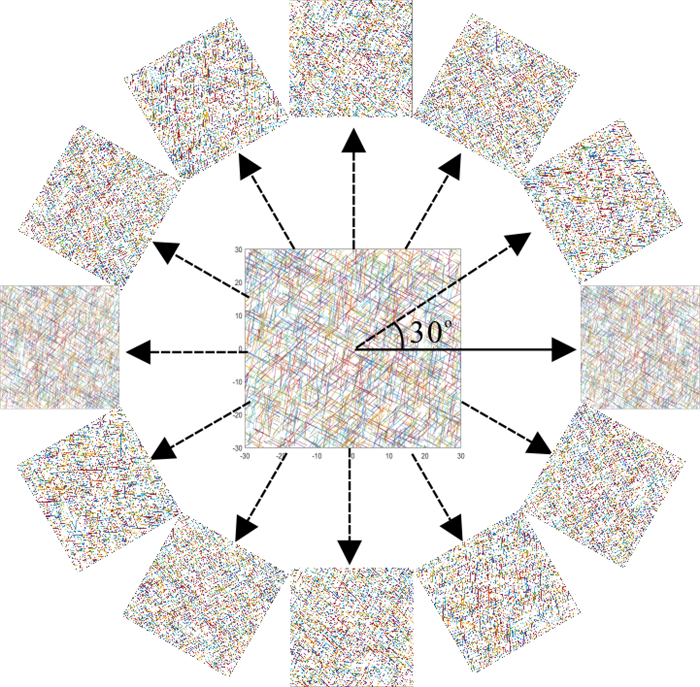
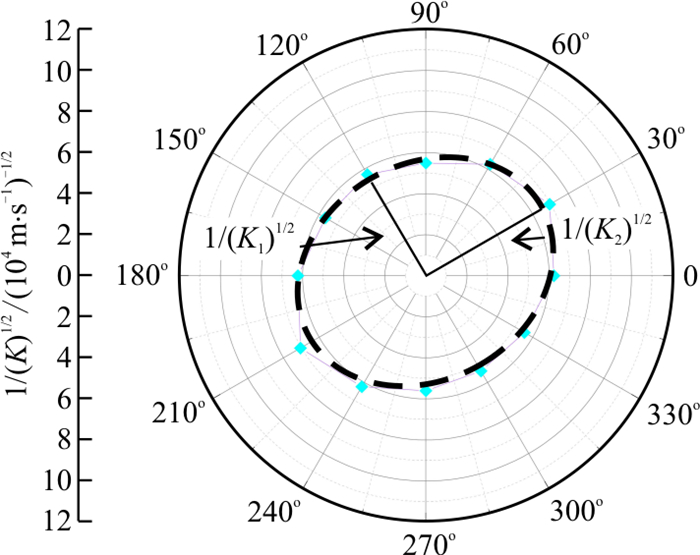
对于本研究的二维裂隙网络稳定渗流问题，求解裂隙介质渗透张量K_ij的具体过程如下：①根据上文所述的离散裂隙网络稳定渗流数学模型方法，在给定的边界条件下计算出计算域沿水力梯度方向上的等效渗透系数。②绕模型中心点旋转裂隙网络，设置为每隔30°旋转一次，共取得12个不同方向的计算域网络模型，并分别计算其沿水力梯度方向上的渗透系数，见图 4。③以12个方向的度数及对应角度所计算出的渗透系数的平方根倒数为坐标点，在极坐标系下采用最小二乘法将这12个点拟合成渗透椭圆，见图 5。④求出渗透椭圆的长半轴和短半轴长度，从而得到裂隙介质的渗透主值K₁、K₂，并根据渗透主值与极坐标的0°方向夹角θ确定渗透主方向，然后由下式计算出渗透张量的分量值：

图  4  裂隙网络模型绕中心点旋转示意图

Figure  4.  Diagram of the fracture network model rotating around the center point

下载: 全尺寸图片 幻灯片

图  5  裂隙网络模型渗透椭圆示意图

Figure  5.  Hydraulic conductivity ellipse diagram of the fracture network model

下载: 全尺寸图片 幻灯片

为了判断计算出的渗透张量能否较准确地表征裂隙网络模型的渗流特征，需要进行均方根误差RMS的计算。RMS是评价拟合过程中渗透系数计算值和渗透椭圆拟合值的拟合程度的一个重要指标，RMS越小代表拟合程度越好，其计算方法如下：

式中：N为不同方向计算出的渗透系数个数，取12；K_g(α)为方向角为α时的渗透系数计算值；K_c(α)为方向角为α时应用最小二乘法拟合出的渗透系数。

3.   渗透性REV分析

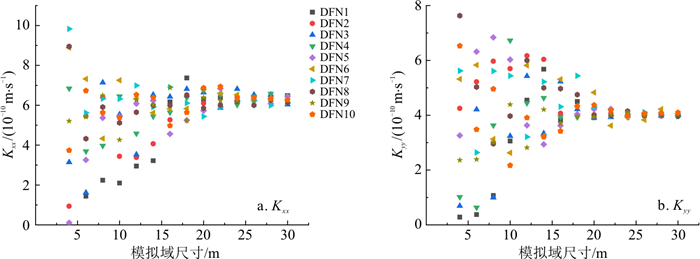
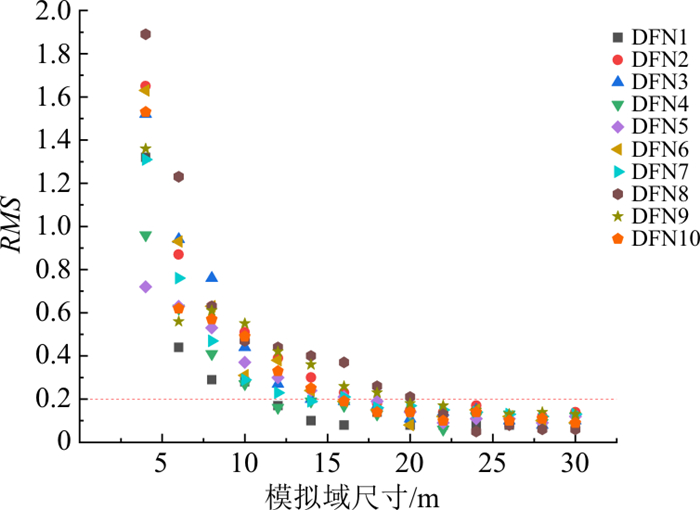
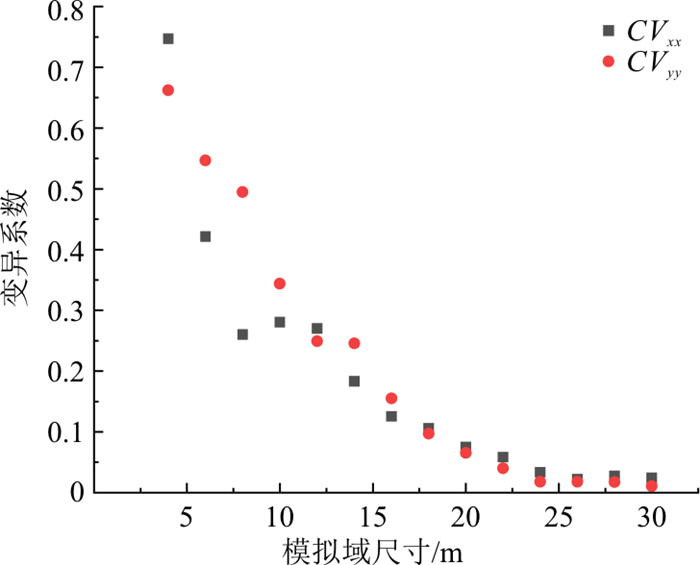
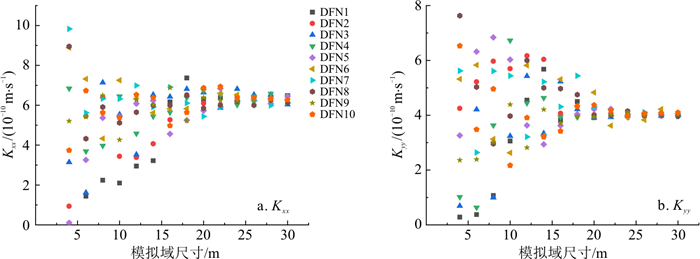
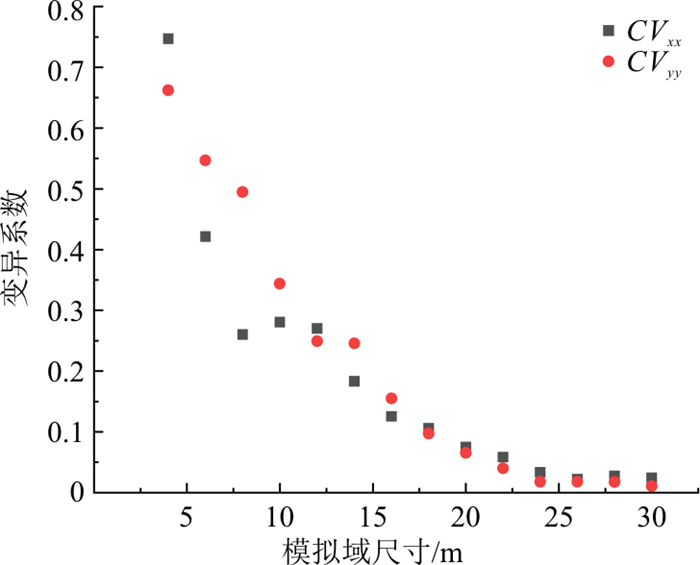
REV是能够从宏观角度反映出研究区某种属性的最小区域。对于本次的裂隙网络稳定渗流模拟研究来说，REV指的是渗透性典型单元体。本研究将根据变尺寸模拟域的渗透性相关参数：渗透张量分量K_xx，K_yy、均方根误差RMS、渗透张量分量的变异系数CV_xx，CV_yy随模拟域尺寸变化情况(如图 6~8所示)分析研究区渗透性REV。其中，为避免分析结果受到Monte-Carlo随机模拟技术生成的裂隙网络模型具有一定的随机性的影响，基于裂隙几何参数统计数据，重复生成了10组60 m×60 m的裂隙网络模型(DFN1~DFN10)，计算域取为30 m×30 m，分别计算了10组DFN模型在变尺寸模拟域(4 m×4 m, 6 m×6 m, ⋯, 30 m×30 m)中的渗透性参数并进行分析。

图  6  渗透张量分量随模拟域尺寸变化图

Figure  6.  Hydraulic conductivity tensor component changes with the size of the simulation domain

下载: 全尺寸图片 幻灯片

图  7  RMS随模拟域尺寸变化图

Figure  7.  RMS variation with the size of the simulation domain

下载: 全尺寸图片 幻灯片

图  8  变异系数随模拟域尺寸变化图

Figure  8.  Coefficient of variation with the size of the simulation domain

下载: 全尺寸图片 幻灯片

当K_xx、K_yy的数值基本稳定时，该裂隙网络模型的渗透性不再发生明显变化，认为此时研究尺寸达到了REV尺寸；根据Öhman等^[20]的研究，当RMS＜0.2时，可认为此时的研究尺寸达到了REV尺寸；对于CV_xx，CV_yy，设定一个容许值，当变异系数小于容许值时，可认为此时的研究尺寸达到了REV尺寸，根据Min等^[21]的研究，变异系数的容许值可取为10%。

结合图 6~8对渗透性参数K_xx，K_yy，RMS，CV_xx，CV_yy随着模拟域尺寸增加而变化的规律进行分析，可以发现10组离散裂隙网络模型的渗透性参数计算结果均显示出了相似的规律。在模拟域尺寸较小时，不同随机裂隙网络计算出的渗透性参数差异较大，各向异性显著；随着模拟域尺寸的增大，渗透性参数差异变小，且都在模拟域边长达到20 m或22 m时达到REV判定临界值，因此考虑到裂隙网络模型生成的随机性，可将该研究区的REV尺寸取为22 m×22 m。在达到REV尺寸后，模拟域可等效为连续介质处理，模拟域计算得到的渗透性参数可以代表研究区的渗透性特征。因此，渗流计算单元尺寸大于REV尺寸时，渗透性参数趋于一致，可以直接应用REV渗透性参数作为研究区内更大尺寸区域的等效渗透性参数进行裂隙介质渗流场模拟。

4.   等效渗透系数升尺度转换

本研究进行升尺度运算时没有考虑渗透主值与渗透主方向的影响，所以升尺度运算仅对裂隙网络旋转角度为0°时的等效渗透系数进行。由于升尺度运算采用4个网格单元的等效渗透系数进行最为合适，所以需改变裂隙网络模型生成域尺寸便于进行升尺度运算。基于裂隙几何参数分布规律及统计数据，设定裂隙网络模型生成域为80 m×80 m，计算域为40 m×40 m。网格单元尺寸极小时，裂隙网络连通性差，等效渗透系数计算结果没有规律性，故取最小网格单元尺寸为5 m×5 m。对裂隙网络模型进行不同尺寸网格化处理(5 m×5 m、10 m×10 m、20 m×20 m)，并对5 m×5 m、10 m×10 m网格单元的等效渗透系数进行升尺度运算。

为了便于区分，将升尺度运算得到的等效渗透系数记为K，5 m×5 m网格单元升尺度运算得到的等效渗透系数记为K₅，10 m×10 m网格单元升尺度运算得到的等效渗透系数记为K₁₀。裂隙网络模型计算得到的10 m×10 m复合网格单元的等效渗透系数记为K₁₀，20 m×20 m复合网格单元的等效渗透系数记为K₂₀。40 m×40 m的计算域可划分为64个5 m×5 m的网格单元，16个10 m×10 m的网格单元，4个20 m×20 m的网格单元，分别计算出10组裂隙网络模型不同尺寸网格单元的等效渗透系数，采用4个5 m×5 m网格单元的等效渗透系数进行升尺度运算以得到K₅与K₁₀对应，4个10 m×10 m网格单元的等效渗透系数进行升尺度运算以得到K₁₀与K₂₀对应。

本研究采用参数升尺度方法中的3种普适性的升尺度方法对5 m×5 m网格单元与10 m×10 m网格单元的等效渗透系数进行升尺度运算，这3种升尺度方法无需确定流动状态，可直观展现出网格单元的等效渗透系数是否具有代表性。

4.1   统计平均法

一个已知渗透系数分布的区块的等效渗透系数是有上限和下限的，其区间的范围由Wiener界限确定(调和平均数=下限，算术平均数=上限)^[22]。通常使用加权平均来描述Wiener界限之间的等效渗透系数范围，见式(8)。

式中: K_eff为等效渗透系数；V为区块体积；p为幂指数，指数范围为-1到1。当p=-1时，上式表示调和平均数K_h(下限)，当p=1时，上式表示算数平均数K_a(上限)，当p无限趋近于0时，上式表示几何平均数K_g。

4.2   标准重整化

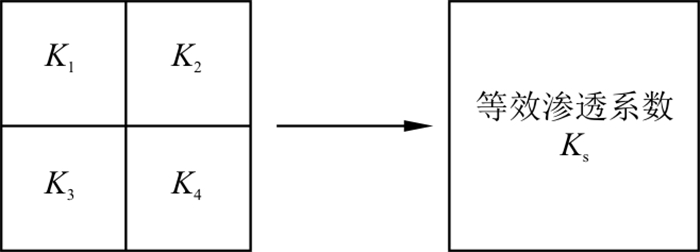
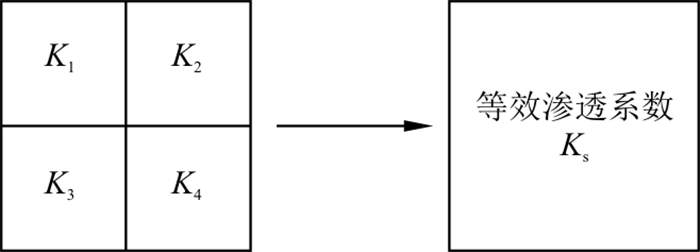
我们称King^[23]提出的升尺度方法为标准重整化，通过类比介质中流体流动与通过电阻的电流流动而提出的一种二维升尺度方法。二维标准重整化升尺度的等效渗透系数K_s是通过一系列连续的4个单元聚合来计算的，如图 9。通过下式来对二维网格单元的等效渗透系数进行升尺度运算：

图  9  二维标准重整化过程示意图

Figure  9.  Schematic diagram of a two-dimensional standard renormalization process

下载: 全尺寸图片 幻灯片

4.3   简化重整化

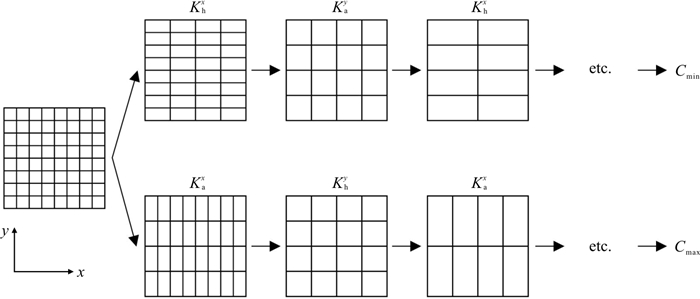
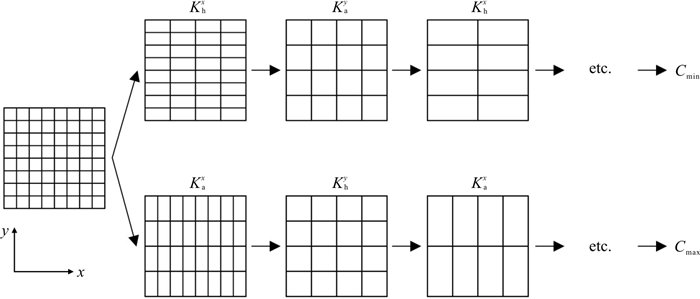
简化重整化方法是在综合了Cardwell & Parsons边界及重整化方法原理的基础上通过迭代算法对相邻单元的等效渗透系数进行组合，算法具体步骤为^{[11, 24]}：在第一步中，根据计算方向交替地以并联和串联的方式对单元进行分组。如果2个单元是串联的，它们被1个唯一的单元取代，等效渗透系数是单元渗透系数的调和平均值K_h^x。如果2个单元是并联的，等效渗透系数是单元渗透系数的算术平均值K_a^y。这个基本过程系统地重复，直到得到1个唯一的值。分组的顺序影响最终结果。在二维中，可以从沿着x方向的串联分组开始，然后沿着y方向并联分组，重复这个基本算法，直到得到一个表示C_min的值，见式(10)；或者可以从沿着y方向并联分组开始，然后沿着x方向串联分组，重复这个算法以得到一个表示C_max的值，见式(11)。具体二维简化重整化过程如图 10所示。

图  10  二维简化重整化过程示意图

Figure  10.  Schematic diagram of a two-dimensional simplified renormalization process

下载: 全尺寸图片 幻灯片

5.   结果与讨论

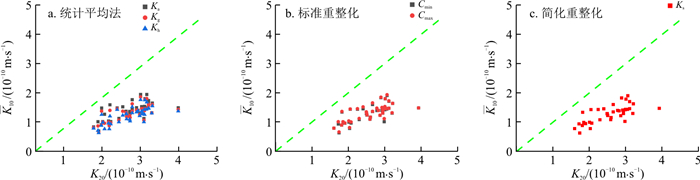
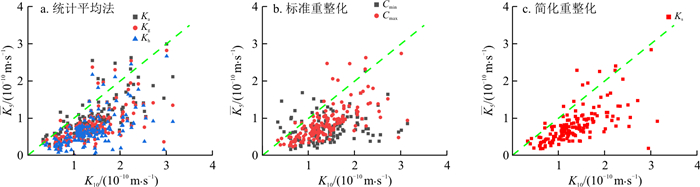
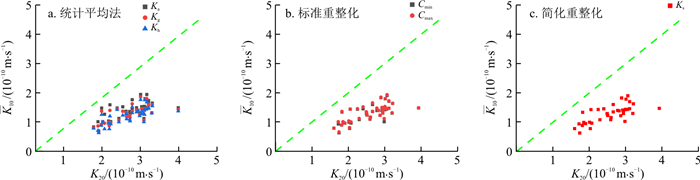
分别计算出10组裂隙网络模型不同尺寸网格单元(5 m×5 m，10 m×10 m，20 m×20 m)的等效渗透系数，通过以上3种升尺度方法对10组裂隙网络模型5 m×5 m网格单元与10 m×10 m网格单元的等效渗透系数进行升尺度运算，运算结果如图 11, 12所示，其中图 11以K₁₀为横坐标，K₅作为纵坐标，图 12以K₂₀为横坐标，K₁₀作为纵坐标，图 11, 12中均添加y=x虚线段。

图  11  m网格单元等效渗透系数升尺度展示图

Figure  11.  Upscaling diagram of the equivalent permeability coefficient of a 5 m grid cell

下载: 全尺寸图片 幻灯片

图  12  10 m网格单元等效渗透系数升尺度展示图

Figure  12.  Upscaling diagram of the equivalent permeability coefficient of a 10 m grid cell

下载: 全尺寸图片 幻灯片

如图 11，12所示，y=x虚线段上仅有极少数散点，拟合情况差。因此，对REV尺寸以下网格单元的等效渗透系数进行升尺度尝试，升尺度方法得到的等效渗透系数与裂隙网络模型复合网格单元计算得到的等效渗透系数有显著差异。因此判定使用REV尺寸以下网格单元的等效渗透系数进行参数升尺度运算不具有实际意义，REV尺寸以下网格单元的等效渗透系数只能代表本网格单元范围的渗透性特征，不具有区域代表性。

此外，在图 11中，有92.4%的散点位于y=x虚线段下部，在图 12中，全部散点位于y=x虚线段下部，可以认为，对于REV尺寸以下网格单元，升尺度方法得到的等效渗透系数往往存在低估的误差。对于裂隙岩体来说，一般情况下试验测量尺度较小，若是在裂隙介质统计数据不充足无法确定REV尺寸的情况下，可以认为对水文地质试验得到的较小尺度区域的渗透系数进行参数升尺度往往是存在低估误差的。只有当较小尺度试验作用在裂隙上时，所得的渗透系数值是偏高的，参数升尺度才可能出现高估的误差。

通过比较图 11，12发现，随着网格单元尺寸增大，程序计算得到的等效渗透系数也增大。这是由于小范围内定义的孤立裂隙和死端裂隙在大范围内可能成为连通裂隙，因此，随着网格单元尺寸逐渐增大，裂隙网络模型中的水流渗流途径逐渐增加，渗透性也随之增大。

诸如地下水封洞库工程渗流场数值模拟过程中，通常会采用分区加密的方式对钻孔、河流、洞室和模型边界附近进行局部加密，控制关键区域网格点距离不超过10 m，其他区域网格点距离最大可达数百米，此时对不同尺寸网格渗透性参数合理赋值便成了难题^{[12, 25]}。根据对裂隙介质渗透性的升尺度转换研究，对此难题提出解决建议：由于结构面的几何特征(产状、密度、迹长、隙宽)对裂隙介质的渗透性REV尺寸均存在一定影响，因此可根据当地地质条件对研究区域分区，统计分析各分区域的裂隙几何特征参数并进行裂隙网络模拟，分析各区域渗透性REV尺寸及其对应渗透系数。对于小于REV尺寸的网格，采用对应区域水文地质试验得到的渗透性参数进行空间变异分析和顺序指示模拟后得到渗透参数场并对网格进行赋值；对于大于REV尺寸的网格，采用对应区域REV的渗透性参数进行赋值。这一建议可为各类相关工程项目中的裂隙介质渗流场数值模拟提供理论依据。

6.   结论

(1) 渗流计算单元尺寸达到渗透性REV尺寸后，计算得到的渗透性参数可以直接代表研究区内更大尺寸区域的渗透性参数，无需进行升尺度运算。数据资料充足的裂隙介质研究区，可根据结构面发育特征不同应用本研究中裂隙网络随机模拟和渗流分析方法确定研究区不同分区渗透性REV，对于大于REV尺寸的网格，可直接采用对应分区REV尺寸的渗透性参数进行赋值。

(2) 渗流计算单元尺寸小于REV尺寸时，裂隙介质的渗透性具有非常强烈的非均质性和各向异性，计算得到的渗透性参数只能代表本单元范围的渗透性特征，无法有效代表研究区内更大尺寸区域的渗透性特征。

(3) 对于地表裂隙测量、地质素描图以及钻孔电视智能成像等数据资料不充足的裂隙介质研究区，往往难以确定研究区渗透性REV，这时对水文地质试验得到的较小尺度区域的渗透系数进行参数升尺度通常会存在低估的误差。