二维承压非稳定流水均衡区间的数值模拟

董贵明; 王颖; 詹红兵; 田娟; 李嘉宁; 代丽娜

doi:10.19509/j.cnki.dzkq.tb20230028

二维承压非稳定流水均衡区间的数值模拟

doi: 10.19509/j.cnki.dzkq.tb20230028

1.
中国矿业大学资源与地球科学学院, 江苏徐州 221116
2.
四川省水资源调度管理中心, 成都 610017
3.
美国德克萨斯农工大学地质与地球物理系, 德克萨斯 77843-3115
4.
江苏师范大学地理测绘与城乡规划学院, 江苏徐州 221116

基金项目:

国家自然科学基金项目 41202179

江苏省生态环境保护地下水监测监控与污染控制重点实验室开放课题 GWKL2201

详细信息

作者简介:
董贵明(1979—), 男, 副教授, 主要从事地下水数值模拟研究工作。E-mail: guiming14432@126.com

中图分类号: P641
计量
- 文章访问数: 559
- PDF下载量: 39
- 被引次数: 0
出版历程
- 收稿日期: 2023-01-17
- 录用日期: 2023-04-07
- 修回日期: 2023-03-31

Numerical simulation of the water budget interval for unsteady two-dimensional confined flow

1.
School of Resources and Geosciences, China University of Mining and Technology, Xuzhou Jiangsu 221116, China
2.
Sichuan Provincial Water Resources Dept., Chengdu 610017, China
3.
Department of Geology and Geophysics, Texas A&M University, TX 77843-3115, USA
4.
Department of Environmental Science, Jiangsu Normal University, Xuzhou Jiangsu 221116, China

摘要

摘要:
由于水文地质条件的复杂性和建模工作投入的有限性, 地下水数值模型往往存在不确定性。近50年来, 随机方法是其不确定性分析的主要方法之一。区间不确定性与随机不确定性不同, 是将水文地质参数等看做区间(范围), 而不再考虑其随机特征。从区间不确定性角度出发, 以非稳定二维承压水流为例, 提出了在已知水文地质参数等为区间的情况下, 基于一阶摄动展开的地下水均衡项区间的数值模拟方法。基于地下水流和污染物迁移三维数值模拟程序GFModel实现了这种方法。算例分析表明, 本研究方法当参数变化率在0.1以内的时候, 偏差相对误差整体上可以控制在10%以内, 该方法的计算效率明显高于等间距连续采样法。该方法的结果中不包含随机统计信息, 但在已知水文地质参数等为区间的情况下, 计算出水均衡项的区间, 将能在地下水资源的利用和保护决策中提供一定的理论依据。
- 地下水数值模拟 /
- 水均衡 /
- 区间 /
- GFModel /
- 不确定性 /
- 非稳定流
Abstract: Objective
Groundwater numerical models often have uncertainties due to the complexity of the hydrogeological conditions and the economic and time constraints in collecting a sufficiently large dataset as inputs for conducting modelling exercises. In the past 50 years, stochastic methods have been one of the main methods of uncertainty analysis. The interval uncertainty is different from the stochastic uncertainty, and it considers the hydrogeological parameters as the intervals (ranges) without considering their stochastic properties.
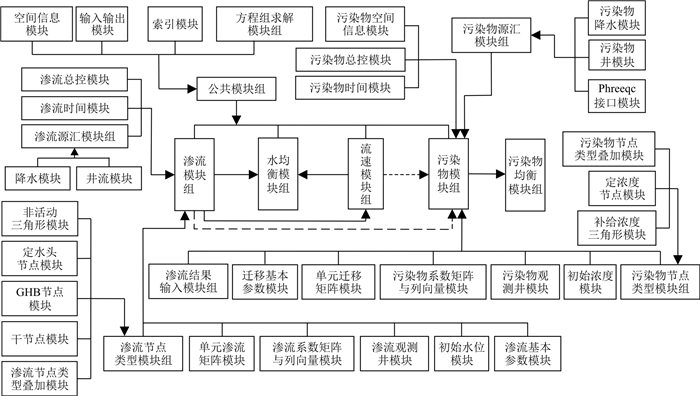
Methods
From the perspective of interval uncertainty, a numerical simulation method based on first-order perturbation expansion was proposed for simulating unsteady two-dimensional confined flow with known hydrogeological parameters as intervals in this paper.The proposed method is implemented based on GFModel, a three-dimensional (3D) numerical simulation platform for groundwater flow and pollutant migration.
Results
The analysis shows that the relative error can be controlled within 10% when the parameter change rate is less than 0.1. The computational efficiency of the proposed method is obviously higher than that of the continuous sampling method with equal spacing.
Conclusion
This method allows the interval of the head or water budget to be calculated without the requirement for detailed statistical information (which is usually unavailable in advance) if the intervals of hydrogeological parameters are known.It provides a theoretical basis for decisions on the use and protection of groundwater resources.
- groundwater numerical simulation /
- water balance /
- interval /
- GFModel /
- uncertainty /
- unsteady flow
注释:

(所有作者声明不存在利益冲突)

HTML全文

图 1 GFModel主要模块及其关系图

Figure 1. Main modules of GFModel and their relationship diagram

下载: 全尺寸图片幻灯片

图 2 模型渗透系数分区图

Figure 2. Zonation of hydraulic conductivities for the groundwater flow model

下载: 全尺寸图片幻灯片

图 3 不同时段地下水均衡区间对比

a, b, c.变化率为0.1; d, e, f.变化率为0.2; g, h, i.变化率为0.3

Figure 3. Comparison of the groundwater budget interval in different time

下载: 全尺寸图片幻灯片

表 1 理想模型含水层各项参数设定

Table 1. Aquifer parameter setting of the hypothetical model

参数	参数值	参数		参数值
含水层厚度/m	20	定水头边界水头/m		70
初始水头/m	80		水头/m	80
顶板高程/m	20	GHB边界	渗透系数/(m·d^-1)	6
底板高程/m	0	GHB边界	距离倒数/m^-1	0.01
贮水率/m^-1	1×10^-4

下载: 导出CSV

表 2 各分区渗透系数数值

Table 2. Hydraulic conductivity setting of each zone

分区号	1	2	3	4	5
渗透系数/(m·d^-1)	7	4	9	5	3

下载: 导出CSV

表 3 各分区观测井信息

Table 3. Observation well information for each zone

观测井编号	X/m	Y/m	观测井编号	X/m	Y/m
O-1	25	78	O-4	74	45
O-2	21	26	O-5	66	72
O-3	61	20

下载: 导出CSV

表 4 理想算例水均衡项(水量单位：m³)

Table 4. Groundwater budget in the hypothetical model

时段	抽水量	GHB边界侧向补给量	定水头边界侧向补给量	弹性释水量	均衡误差/ 10^-2
1	-5.00	5.06	-88.91	-88.85	0.00
2	-5.00	7.24	-40.33	-38.09	0.00
3	-5.00	8.48	-23.59	-20.11	0.00
4	-5.00	9.22	-15.49	-11.26	0.00
5	-5.00	9.67	-11.10	-6.43	0.00
6	-5.00	9.93	-8.63	-3.70	0.00
7	-5.00	10.09	-7.22	-2.13	0.00
8	-5.00	10.18	-6.41	-1.23	0.00
9	-5.00	10.23	-5.94	-0.71	0.00
10	-5.00	10.26	-5.67	-0.41	0.00
总计	-50.00	90.35	-213.30	-172.95	0.00
注：1.水量流入模拟区为+，流出为-；2.均衡误差=边界侧向补给量(GHB边界+定水头边界)-弹性释水量+抽水量

下载: 导出CSV

参考文献(29)

[1]	Sreekanth J, Moore C. Novel patch modelling method for efficient simulation and prediction uncertainty analysis of multi-scale groundwater flow and transport processes[J]. Journal of Hydrology, 2018, 559: 122-135. doi: 10.1016/j.jhydrol.2018.02.028
[2]	薛佩佩, 文章, 梁杏. 地质统计学在含水层参数空间变异研究中的应用进展与发展趋势[J]. 地质科技通报, 2022, 41(1): 209-222. doi: 10.19509/j.cnki.dzkq.2022.0015 Xue P P, Wen Z, Liang X. Application and development trend of geostatistics in the research of spatial variation of aquifer parameters[J]. Bulletin of Geological Science and Technology, 2022, 41(1): 209-222(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2022.0015
[3]	肖景红, 王敏, 王川, 等. 含优势渗流层边坡降雨入渗下的可靠度分析[J]. 地质科技通报, 2021, 40(6): 193-204. doi: 10.19509/j.cnki.dzkq.2021.0619 Xiao J H, Wang M, Wang C, et al. Reliability analysis of slope with dominant seepage interlayer under rainfall infiltration[J]. Bulletin of Geological Science and Technology, 2021, 40(6): 193-204(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2021.0619
[4]	孙晓卓, 曾献奎, 吴吉春, 等. 一种改进的地下水模型结构不确定性分析方法[J]. 水文地质工程地质, 2021, 48(6): 24-33. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG202106003.htm Sun X Z, Zeng X K, Wu J C, et al. An improved method for the structural uncertainty analysis of groundwater models[J]. Hydrogeology and Engineering Geology, 2021, 48(6): 24-33(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG202106003.htm
[5]	Niklas L, David G, James I, et al. On uncertainty quantification in hydrogeology and hydrogeophysics[J]. Advances in Water Resources, 2017, 110: 166-181. doi: 10.1016/j.advwatres.2017.10.014
[6]	钟乐乐, 曾献奎, 吴吉春. 基于高斯过程回归的地下水模型结构不确定性分析与控制[J]. 水文地质工程地质, 2019, 46(1): 1-10. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201901001.htm Zhong L L, Zeng X K, Wu J C. Analysis and control of structural uncertainty of groundwater model based on Gaussian process regression[J]. Hydrogeology and Engineering Geology, 2019, 46(1): 1-10(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201901001.htm
[7]	Sreekanth J, Catherine M. Novel patch modelling method for efficient simulation and prediction uncertainty analysis of multi-scale groundwater flow and transport processes[J]. Journal of Hydrology, 2018, 559: 122-135. doi: 10.1016/j.jhydrol.2018.02.028
[8]	Ata J, Mohammad Z, Ali N Z, et al. Groundwater management under uncertainty using a stochastic multi-cell model[J]. Journal of Hydrology, 2017, 551(S1): 265-277.
[9]	Kifanyi G E, Ndambuki J M, Odai S N, et al. Quantitative management of groundwater resources in regional aquifers under uncertainty: A retrospective optimization approach[J]. Groundwater for Sustainable Development, 2019, 8: 530-540. doi: 10.1016/j.gsd.2019.02.005
[10]	Sreekanth J, Catherine M, Leif W. Pareto-based efficient stochastic simulation-optimization for robust and reliable groundwater management[J]. Journal of Hydrology, 2016, 533: 180-190. doi: 10.1016/j.jhydrol.2015.12.001
[11]	Chen M J, Izady A, Abdalla O A, et al. A surrogate-based sensitivity quantification and Bayesian inversion of a regional groundwater flow model[J]. Journal of Hydrology, 2018, 557: 826-837.
[12]	Tang Z C, Lu Z Z, Wang P, et al. Efficient numerical simulation method for evaluations of global sensitivity analysis with parameter uncertainty[J]. Applied Mathematical Modelling, 2016, 40(1): 597-611.
[13]	徐亚宁, 卢文喜, 王梓博, 等. 考虑参数和边界条件不确定性的地下水污染随机模拟[J]. 中国环境科学, 2022, 42(7): 3244-3253. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHJ202207028.htm Xu Y N, Lu W X, Wang Z B, et al. Stochastic simulation of groundwater pollution considering uncertainty of parameters and boundary conditions[J]. China Environmental Science, 2022, 42(7): 3244-3253(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHJ202207028.htm
[14]	Han F, Zheng Y. Joint analysis of input and parametric uncertainties in watershed water quality modeling: A formal Bayesian approach[J]. Advances in Water Resources, 2018, 116: 77-94.
[15]	Joseph J, Ghosh S, Pathak A, et al. Hydrologic impacts of climate change: Comparisons between hydrological parameter uncertainty and climate model uncertainty[J]. Journal of Hydrology, 2018, 566: 1-22.
[16]	Marchant B, Mackay J, Bloomfield J. Quantifying uncertainty in predictions of groundwater levels using formal likelihood methods[J]. Journal of Hydrology, 2016, 540: 699-711.
[17]	Xie Y Q, Cook P G, Simmons C T, et al. Uncertainty of groundwater recharge estimated from a water and energy balance model[J]. Journal of Hydrology, 2018, 561: 1081-1093.
[18]	Albert C L, Merigó J M, Xu Y J. A coupled stochastic inverse sharp interface seawater intrusion approach for coastal aquifers under groundwater parameter uncertainty[J]. Journal of Hydrology, 2016, 540: 774-783.
[19]	Moore R E. Interval analysis[M]. Englewood Cliffs, New Jersey: Prentice-Hall, 1966.
[20]	Xie Y, Li Y, Huang G, et al. An interval fixed-mix stochastic programming method for greenhouse gas mitigation in energy systems under uncertainty[J]. Energy, 2010, 35(12): 4627-4644.
[21]	Gao W, Wu D, Song C, et al. Hybrid probabilistic interval analysis of bar structures with uncertainty using a mixed perturbation Monte-Carlo method[J]. Finite Elements in Analysis and Design, 2011, 47(7): 643-652.
[22]	Miao D, Huang W, Li Y, et al. Planning water resources systems under uncertainty using an interval-fuzzy De novo programming method[J]. Journal of Environmental Informatics, 2014, 24(1): 11-23.
[23]	Lü Z, Qiu Z Q. An iteration method for predicting static response of nonlinear structural systems with non-deterministic parameters[J]. Applied Mathematical Modelling, 2019, 68: 48-65.
[24]	Qiu Z Q, Xia H J. A novel interval linear programming based on probabilistic dominance[J]. Fuzzy and Systems, 2021, 434(S1): 20-47.
[25]	Dong G M, Tian J, Zhan H, et al. Groundwater flow determination using an interval parameter perturbation method[J]. Water, 2017, 9(12): 978.
[26]	Dong G M, Wang Y, Tian J, et al. Nonlinear expression of groundwater head interval based on the perturbation method[J]. Journal of Hydrologic Engineering, 2021, 26(8): 04021025.
[27]	Dong G M, Wang Y, Tian J, et al. Groundwater head uncertainty analysis in unsteady-state water flow models using the interval and perturbation methods[J]. Hydrogeology Journal, 2021, 29 (5): 1871-1883.
[28]	邱志平, 王晓军. 不确定性结构力学问题的集合理论凸方法[M]. 北京: 科学出版社, 2008. Qiu Z P, Wang X J. Convex method of set theory for uncertain structural mechanics problems[M]. Beijing: Science Press, 2008(in Chinese).
[29]	王颍. 二维承压水流地下水均衡项的区间分析方法及应用研究[D]. 江苏徐州: 中国矿业大学, 2020. Wang Y. Interval analysis method and application research of two-dimensional confined flow groundwater equilibrium term[D]. Xuzhou Jiangsu: China University of Mining and Technology, 2020(in Chinese with English abstract).