基于微观连续介质模型的反应溶质运移数值模拟方法

张倩; 董艳辉

doi:10.19509/j.cnki.dzkq.tb20230081

基于微观连续介质模型的反应溶质运移数值模拟方法

doi: 10.19509/j.cnki.dzkq.tb20230081

张倩^{1, 2, 3,},
董艳辉^{1, 2, 3, ,}

1.
中国科学院地质与地球物理研究所, 中国科学院页岩气与地质工程重点实验室, 北京 100029
2.
中国科学院地球科学研究院, 北京 100029
3.
中国科学院大学, 地球与行星科学学院, 北京 100049

基金项目:

国家自然青年科学基金项目 42202285

详细信息

作者简介:
张倩, E-mail: zhangqian@mail.iggcas.ac.cn

通讯作者:
董艳辉, E-mail: dongyh@mail.iggcas.ac.cn

中图分类号: P641.2;X143
计量
- 文章访问数: 706
- PDF下载量: 69
- 被引次数: 0
出版历程
- 收稿日期: 2023-02-16
- 录用日期: 2023-06-25
- 修回日期: 2023-06-17

Numerical simulation method for reactive solute transport based on micro-continuum medium model

ZHANG Qian^{1, 2, 3
,},
DONG Yanhui^{1, 2, 3
, ,}

1.
Key Laboratory of Shale Gas and Geoengineering, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
2.
Innovation Academy of Earth Science, Chinese Academy of Sciences, Beijing 100029, China
3.
College of Earth and Planetary Science, University of Chinese Academy of Sciences, Beijing 100049, China

More Information

Author Bio:
ZHANG Qian, E-mail: zhangqian@mail.iggcas.ac.cn

Corresponding author: DONG Yanhui, E-mail: dongyh@mail.iggcas.ac.cn

摘要

摘要:
地下环境中流固间的反应溶质运移过程控制着地质介质演化规律, 并受岩石固有非均质性的影响, 衍生出非线性行为与多尺度效应。为了面向更为复杂化的应用需求, 解析微观特征与表观行为间的响应-反馈机制成为了重要的科学与工程命题。本研究系统地介绍了微观连续介质概念与模型框架, 以及该模型方法的实现方式, 并归纳了其在不同研究体系中的应用实例, 最后重点分析了该方法在实验-数值联合研究中的发展前景与预期挑战。数值模拟方法已被广泛应用于反应溶质运移过程的定量研究之中, 但单一孔隙或达西尺度数值模型难以应对机理研究与实例应用间的时空尺度跨度。近年来多尺度数值模拟方法体系不断发展, 其中将Darcy-Brinkman-Stokes方程作为多流态数学统一表达, 以微观连续介质模型作为多尺度信息关联方式的数值模拟框架, 在流固界面追踪、高效数值求解等方面展现出一定的方法优势与应用潜力。
- 反应溶质运移 /
- 微观连续介质方法 /
- 多尺度数值模拟 /
- 机理解析
Abstract: Significance
Fluid-solid interactions in reactive solute transport processes, governed by physical and chemical heterogeneities, dictate the evolution of subsurface geomaterials, resulting in nonlinear behaviours and multiscale features. It has become increasingly evident that examining the feedback between microscopic features and macroscopic behaviours in geomaterials is critical in various academic and industrial applications.
Progress
In this study, we introduce the concept and framework, mathematical and numerical models of the micro-continuum medium, as well as multiscale solvers and applications. Challenges in co-designed simulations and experiments are also discussed.
Conclusion and Prospects
Despite offering valuable insights into reactive transport processes, continuum-scale modelling or pore-scale modelling suffers from a gap between theoretical understanding and computational prediction. Recently, an alternative conceptualization of the multiscale problem involves the implementation of the Darcy-Brinkman-Stokes (DBS) equation in a single micro-continuum domain to identify reactive transport patterns across spatial scales under changing flow regimes. As fluid-solid interfaces cannot be explicitly resolved as in pore-scale models, the micro-continuum medium approach has the advantage of accommodating complex geometries or evolving interfaces without increasing computational costs.
- reactive solute transport /
- micro-continuum medium approach /
- multiscale numerical simulation /
- mechanistic understanding
注释:

所有作者声明不存在利益冲突。

HTML全文

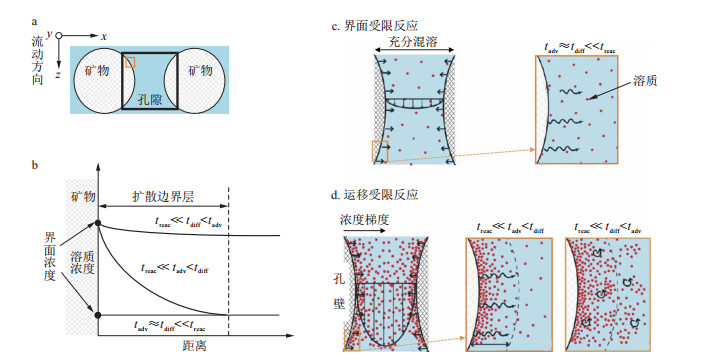
图 1 微观层次特征时间影响下的反应溶质运移模式示意图(据文献[6]修改)

a.孔隙结构概念图；b.不同反应模式下流固界面附近的浓度分布；c, d.2类反应模式主控机制示意图。
t_adv为对流特征时间；t_diff为扩散特征时间；t_reac为反应特征时间

Figure 1. Schematic diagram of reactive solute transport phenomena from a microscopic characteristic time

下载: 全尺寸图片幻灯片

图 2 多尺度数值模拟方法构建示意图

a.多尺度介质结构示意图; b.多尺度介质流态转换示意图; c.微观连续介质空间离散方法示意图

Figure 2. Schematic diagram of multiscale numerical simulation modeling

下载: 全尺寸图片幻灯片

图 3 不同模拟界面求解流程图

a.GeoChemFoam模拟界面；b.COMSOL-CrunchFlow模拟界面

Figure 3. Solution procedure of different modeling interfaces

下载: 全尺寸图片幻灯片

图 4 反应速率与扩散系数变化下的碳酸岩溶蚀演化模式(据文献[31]修改)

a.反应溶质运移模式图；b.面状溶蚀模式；c.锥状蚓孔模式；d.单枝蚓孔模式；e.分枝状蚓孔模式；f.均匀溶蚀模式; Pe, Da_Ⅰ.无量纲参数

Figure 4. Calcite dissolution pattern controlled by different reaction rates and diffusion coefficients

下载: 全尺寸图片幻灯片

图 5 非均质介质中生物膜生长特征模拟(据文献[32]修改)

a.微米CT灰度图像；b.孔隙度空间分布；c.不同模型硝酸盐穿透曲线对比

Figure 5. Numerical investigation of biofilm growth in heterogeneous porous media

下载: 全尺寸图片幻灯片

图 6 裂隙型介质溶蚀过程中的隙宽及浓度场演化(据文献[51]修改)

a.裂隙隙宽及浓度场演化；b.裂隙-不可渗透基质的演化过程；c.裂隙-可渗透基质的演化过程

Figure 6. Evolution of fracture aperture and concentrations in fracture media during dissolution

下载: 全尺寸图片幻灯片

图 7 裂隙型白云岩溶蚀演化特征数值模拟结果(据文献[42]修改)

a. 80 h酸蚀后的裂隙面与改造层空间结构; b. 80 h酸蚀后裂隙-孔隙介质中流场分布; c.80 h多矿物反应速率剖面(纵横比2∶1)

Figure 7. Numerical simulation results of fractured dolomite dissolution evolution

下载: 全尺寸图片幻灯片

参考文献(56)

[1]	BULTREYS T, DE BOEVER W, CNUDDE V. Imaging and image-based fluid transport modeling at the pore scale in geological materials: A practical introduction to the current state-of-the-art[J]. Earth-Science Reviews, 2016, 155: 93-128. doi: 10.1016/j.earscirev.2016.02.001
[2]	BECKINGHAM L E, STEEFEL C I, SWIFT A M, et al. Evaluation of accessible mineral surface areas for improved prediction of mineral reaction rates in porous media[J]. Geochimica et Cosmochimica Acta, 2017, 205: 31-49. doi: 10.1016/j.gca.2017.02.006
[3]	STEEFEL C I, APPELO C A J, ARORA B, et al. Reactive transport codes for subsurface environmental simulation[J]. Computational Geosciences, 2015, 19(3): 445-478. doi: 10.1007/s10596-014-9443-x
[4]	GUALDA G A R, BAKER D R, POLACCI M. Introduction: Advances in 3D imaging and analysis of geomaterials[J]. Geosphere, 2010, 6(5): 468-469. doi: 10.1130/GES00639.1
[5]	姚军, 孙海, 李爱芬, 等. 现代油气渗流力学体系及其发展趋势[J]. 科学通报, 2018, 63(4): 425-451. https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB201804006.htm YAO J, SUN H, LI A F, et al. Modern system of multiphase flow in porous media and its development trend[J]. Chinese Science Bulletin, 2018, 63(4): 425-451. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB201804006.htm
[6]	NOIRIEL C, DAVAL D. Pore-scale geochemical reactivity associated with CO₂ storage: New frontiers at the fluid-solid interface[J]. Accounts of Chemical Research, 2017, 50(4): 759-768. doi: 10.1021/acs.accounts.7b00019
[7]	STEEFEL C I, BECKINGHAM L E, LANDROT G. Micro-continuum approaches for modeling pore-scale geochemical processes[J]. Reviews in Mineralogy and Geochemistry, 2015, 80(1): 217-246. doi: 10.2138/rmg.2015.80.07
[8]	PEREZ L J, HIDALGO J J, PUYGUIRAUD A, et al. Assessment and prediction of pore-scale reactive mixing from experimental conservative transport data[J]. Water Resources Research, 2020, 56(6): e2019WR026452. doi: 10.1029/2019WR026452
[9]	YOON S, KANG P K. Mixing-induced bimolecular reactive transport in rough channel flows: Pore-scale simulation and stochastic upscaling[J]. Transport in Porous Media, 2023, 146(1): 329-350. http://www.nstl.gov.cn/paper_detail.html?id=18e5c713619af2bd0fadcd8441c1c201
[10]	DENG H, MOLINS S, STEEFEL C, et al. A 2.5D reactive transport model for fracture alteration simulation[J]. Environmental Science & Technology, 2016, 50(14): 7564-7571.
[11]	DENG H, VOLTOLINI M, MOLINS S, et al. Alteration and erosion of rock matrix bordering a carbonate-rich shale fracture[J]. Environmental Science & Technology, 2017, 51(15): 8861-8868.
[12]	SPOKAS K, PETERS C A, PYRAK-NOLTE L. Influence of rock mineralogy on reactive fracture evolution in carbonate-rich caprocks[J]. Environmental Science & Technology, 2018, 52(17): 10144-10152.
[13]	施斌. 论工程地质中的场及其多场耦合[J]. 工程地质学报, 2013, 21(5): 673-680. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201305001.htm SHI B. On fields and their coupling in engineering geology[J]. Journal of Engineering Geology, 2013, 21(5): 673-680. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201305001.htm
[14]	MOLINSS, TREBOTICH D, STEEFEL C I, et al. An investigation of the effect of pore scale flow on average geochemical reaction rates using direct numerical simulation[J]. Water Resources Research, 2012, 48(3): W03527.
[15]	MEHMANI A, VERMA R, PRODANOVIĈ M. Pore-scale modeling of carbonates[J]. Marine and Petroleum Geology, 2020, 114: 104141. doi: 10.1016/j.marpetgeo.2019.104141
[16]	DÁVILA G, LUQUOT L, SOLER J M, et al. Interaction between a fractured marl caprock and CO₂-rich sulfate solution under supercritical CO₂ conditions[J]. International Journal of Greenhouse Gas Control, 2016, 48: 105-119. doi: 10.1016/j.ijggc.2015.11.005
[17]	LI L, STEEFEL C I, YANG L. Scale dependence of mineral dissolution rates within single pores and fractures[J]. Geochimica et Cosmochimica Acta, 2008, 72(2): 360-377. doi: 10.1016/j.gca.2007.10.027
[18]	STEEFEL C I, MOLINS S, TREBOTICH D. Pore scale processes associated with subsurface CO₂ injection and sequestration[J]. Reviews in Mineralogy and Geochemistry, 2013, 77(1): 259-303. doi: 10.2138/rmg.2013.77.8
[19]	BLUNT M J, BIJELJIC B, DONG H, et al. Pore-scale imaging and modelling[J]. Advances in Water Resources, 2013, 51: 197-216. doi: 10.1016/j.advwatres.2012.03.003
[20]	ANOVITZ L M, COLE D R. Characterization and analysis of porosity and pore structures[J]. Reviews in Mineralogy and Geochemistry, 2015, 80(1): 61-164. doi: 10.2138/rmg.2015.80.04
[21]	OTT H, OEDAI S. Wormhole formation and compact dissolution in single-and two-phase CO₂-brine injections[J]. Geophysical Research Letters, 2015, 42(7): 2270-2276. doi: 10.1002/2015GL063582
[22]	HORSTEMEYER M F. Multiscale modeling: A review[M]. Dordrecht: Springer, 2009: 87-135.
[23]	KIM D, LINDQUIST W B. Dependence of pore-to-core up-scaled reaction rate on flow rate in porous media[J]. Transport in Porous Media, 2011, 89(3): 459-473. doi: 10.1007/s11242-011-9780-3
[24]	MATOUŠ K, GEERS M G D, KOUZNETSOVA V G, et al. A review of predictive nonlinear theories for multiscale modeling of heterogeneous materials[J]. Journal of Computational Physics, 2017, 330: 192-220. doi: 10.1016/j.jcp.2016.10.070
[25]	YOUSEFZADEH M, BATTIATO I. Physics-based hybrid method for multiscale transport in porous media[J]. Journal of Computational Physics, 2017, 344: 320-338. doi: 10.1016/j.jcp.2017.04.055
[26]	DENG H, STEEFEL C, MOLINS S, et al. Fracture evolution in multimineral systems: The role of mineral composition, flow rate, and fracture aperture heterogeneity[J]. ACS Earth and Space Chemistry, 2018, 2(2): 112-124. doi: 10.1021/acsearthspacechem.7b00130
[27]	BRINKMAN H C. A calculation of the viscosity and the sedimentation constant for solutions of large chain molecules taking into account the hampered flow of the solvent through these molecules[J]. Physica, 1947, 13(8): 447-448. doi: 10.1016/0031-8914(47)90030-X
[28]	GOLFIER F, ZARCONE C, BAZIN B, et al. On the ability of a Darcy-scale model to capture wormhole formation during the dissolution of a porous medium[J]. Journal of Fluid Mechanics, 2002, 457: 213-254. doi: 10.1017/S0022112002007735
[29]	GULBRANSEN A F, HAUGE V L, LIE K A. A multiscale mixed finite-element method for vuggy and naturally fractured reservoirs[J]. SPE Journal, 2010, 15(2): 395-403. doi: 10.2118/119104-PA
[30]	SOULAINE C, TCHELEPI H A. Micro-continuum approach for pore-scale simulation of subsurface processes[J]. Transport in Porous Media, 2016, 113(3): 431-456. doi: 10.1007/s11242-016-0701-3
[31]	SOULAINE C, ROMAN S, KOVSCEK A, et al. Mineral dissolution and wormholing from a pore-scale perspective[J]. Journal of Fluid Mechanics, 2017, 827: 457-483. doi: 10.1017/jfm.2017.499
[32]	YAN Z F, LIU C X, LIU Y Y, et al. Multiscale investigation on biofilm distribution and its impact on macroscopic biogeochemical reaction rates[J]. Water Resources Research, 2017, 53(11): 8698-8714. doi: 10.1002/2017WR020570
[33]	成建梅, 罗一鸣. 岩溶多重介质地下水模拟技术及应用进展[J]. 地质科技通报, 2022, 41(5): 220-229. doi: 10.19509/j.cnki.dzkq.2022.0220 CHENG J M, LUO Y M. Overview of groundwater modeling technology and its application in karst areas with multiple-void media[J]. Bulletin of Geological Science and Technology, 2022, 41(5): 220-229. (in Chinese with English abstract) doi: 10.19509/j.cnki.dzkq.2022.0220
[34]	郑小康, 杨志兵. 岩溶含水层饱和-非饱和流动与污染物运移数值模拟[J]. 地质科技通报, 2022, 41(5): 357-366. doi: 10.19509/j.cnki.dzkq.2022.0211 ZHENG X K, YANG Z B. Numerical simulation of saturated-unsaturated groundwater flow and contaminant transport in a karst aquifer[J]. Bulletin of Geological Science and Technology, 2022, 41(5): 357-366. (in Chinese with English abstract) doi: 10.19509/j.cnki.dzkq.2022.0211
[35]	MOLINS S, TREBOTICH D, MILLER G H, et al. Mineralogical and transport controls on the evolution of porous media texture using direct numerical simulation[J]. Water Resources Research, 2017, 53(5): 3645-3661. doi: 10.1002/2016WR020323
[36]	SZYMCZAK P, LADD A J C. Microscopic simulations of fracture dissolution[J]. Geophysical Research Letters, 2004, 31(23): L23606.
[37]	MOLINS S. Reactive interfaces in direct numerical simulation of pore-scale processes[J]. Reviews in Mineralogy and Geochemistry, 2015, 80(1): 461-481. doi: 10.2138/rmg.2015.80.14
[38]	许天福, 金光荣, 岳高凡, 等. 地下多组分反应溶质运移数值模拟: 地质资源和环境研究的新方法[J]. 吉林大学学报(地球科学版), 2012, 42(5): 1410-1425. https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ201205015.htm XU T F, JIN G R, YUE G F, et al. Subsurface reactive transport modeling: A new research approach for geo-resources and environments[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(5): 1410-1425. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ201205015.htm
[39]	SOULAINE C, GJETVAJ F, GARING C, et al. The impact of sub-resolution porosity of X-ray microtomography images on the permeability[J]. Transport in Porous Media, 2016, 113(1): 227-243. doi: 10.1007/s11242-016-0690-2
[40]	DENG H, SPYCHER N. Modeling reactive transport processes in fractures[J]. Reviews in Mineralogy and Geochemistry, 2019, 85(1): 49-74. doi: 10.2138/rmg.2019.85.3
[41]	黄朝琴. 基于离散缝洞网络模型的多尺度两相流动模拟理论研究[D]. 山东青岛: 中国石油大学(华东), 2012. HUANG Z Q. Theoretical study on multiscale modeling of two-phase flow based on discrete fracture-vug network model[D]. Qingdao Shandong: China University of Petroleum (East China), 2012. (in Chinese with English abstract)
[42]	ZHANG Q, DENG H, DONG Y H, et al. Investigation of coupled processes in fractures and the bordering matrix via a micro-continuum reactive transport model[J]. Water Resources Research, 2022, 58(2): e2021WR030578. doi: 10.1029/2021WR030578
[43]	STEEFEL C I, LASAGA A C. A coupled model for transport of multiple chemical species and kinetic precipitation/dissolution reactions with application to reactive flow in single phase hydrothermal systems[J]. American Journal of Science, 1994, 294(5): 529-592. doi: 10.2475/ajs.294.5.529
[44]	LASAGA A C. Chapter 4. Transition state theory[M]. Berlin, Boston: De Gruyter, 1981: 135-170.
[45]	SOULAINE C, PAVULURI S, CLARET F, et al. porous-Media 4Foam: Multi-scale open-source platform for hydro-geochemical simulations with OpenFOAM[J]. Environmental Modelling & Software, 2021, 145: 105199.
[46]	MAES J, MENKE H P. GeoChemFoam: Direct modelling of multiphase reactive transport in real pore geometries with equilibrium reactions[J]. Transport in Porous Media, 2021, 139(2): 271-299. doi: 10.1007/s11242-021-01661-8
[47]	JYOTI A, HAESE R R. Validation of a multicomponent reactive-transport model at pore scale based on the coupling of COMSOL and PhreeqC[J]. Computers & Geosciences, 2021, 156: 104870.
[48]	YOU J H, LEE K J. Pore-scale study to analyze the impacts of porous media heterogeneity on mineral dissolution and acid transport using darcy-brinkmann-stokes method[J]. Transport in Porous Media, 2021, 137(3): 575-602. doi: 10.1007/s11242-021-01577-3
[49]	MOLINS S, SOULAINE C, PRASIANAKIS N I, et al. Simulation of mineral dissolution at the pore scale with evolving fluid-solid interfaces: Review of approaches and benchmark problem set[J]. Computational Geosciences, 2021, 25(4): 1285-1318. doi: 10.1007/s10596-019-09903-x
[50]	MAES J, SOULAINE C, MENKE H P. Improved volume-of-solid formulations for micro-continuum simulation of mineral dissolution at the pore-scale[J]. Frontiers in Earth Science, 2022, 10: 917931. doi: 10.3389/feart.2022.917931
[51]	NOIRIEL C, SOULAINE C. Pore-scale imaging and modelling of reactive flow in evolving porous media: Tracking the dynamics of the fluid-rock interface[J]. Transport in porous media, 2021, 140(1): 181-213. doi: 10.1007/s11242-021-01613-2
[52]	MOLINS S, KNABNER P. Multiscale approaches in reactive transport modeling[J]. Reviews in Mineralogy and Geochemistry, 2019, 85(1): 27-48. doi: 10.2138/rmg.2019.85.2
[53]	CARRILLO F J, BOURG I C, SOULAINE C. Multiphase flow modeling in multiscale porous media: An open-source micro-continuum approach[J]. Journal of Computational Physics: X, 2020, 8: 100073. doi: 10.1016/j.jcpx.2020.100073
[54]	SOULAINE C, CREUX P, TCHELEPI H A. Micro-continuum framework for pore-scale multiphase fluid transport in shale formations[J]. Transport in Porous Media, 2019, 127(1): 85-112. doi: 10.1007/s11242-018-1181-4
[55]	GUO B, MA L, TCHELEPI H A. Image-based micro-continuum model for gas flow in organic-rich shale rock[J]. Advances in Water Resources, 2018, 122: 70-84. doi: 10.1016/j.advwatres.2018.10.004
[56]	LI P, DENG H, MOLINS S. The effect of pore-scale two-phase flow on mineral reaction rates[J]. Frontiers in Water, 2022, 3: 734518. doi: 10.3389/frwa.2021.734518