基于三维裂隙网络模拟和单孔压水试验的裂隙张开度确定方法

程锦波; 夏露; 于青春

doi:10.19509/j.cnki.dzkq.tb20230128

基于三维裂隙网络模拟和单孔压水试验的裂隙张开度确定方法

doi: 10.19509/j.cnki.dzkq.tb20230128

中国地质大学(北京)水资源与环境学院, 北京 100083

详细信息

作者简介:
程锦波, E-mail: cjb@cugb.edu.cn

通讯作者:
于青春, E-mail: yuqch@cugb.edu.cn

中图分类号: P641.135
计量
- 文章访问数: 353
- PDF下载量: 84
- 被引次数: 0
出版历程
- 收稿日期: 2023-03-13
- 录用日期: 2023-06-26
- 修回日期: 2023-04-28

Determination method of fracture aperture based on three-dimensional fracture network simulation and water injection tests

College of Water Resources and Environment, China University of Geosciences(Beijing), Beijing 100083, China

More Information

Author Bio:
CHENG Jinbo, E-mail: cjb@cugb.edu.cn

Corresponding author: YU Qingchun, E-mail: yuqch@cugb.edu.cn

摘要

摘要:
岩体裂隙的等效水力张开度(水力学等效隙宽)是岩体的关键力学几何参数之一。目前常采用交叉孔试验等大型试验方法获取野外深部岩体裂隙的张开度, 但该方法很少在一个工程中多次使用, 且难以分析裂隙张开度在空间上的变化。以三峡大坝右岸地下电站硐室围岩为例, 提出了一种联合利用常规单孔压水试验数据和三维裂隙网络模拟, 反演确定裂隙等效水力张开度的新方法。利用实测裂隙编录资料取得的统计数据开展裂隙产状随机模拟, 构建与压水试验钻孔连通的三维离散裂隙网络渗流模型, 拟合单孔压水稳态流量和压力的关系, 反演不同深度岩体的裂隙等效水力张开度。结果表明, 研究区岩体裂隙的等效水力张开度一般为0.07~0.30 mm, 符合对数正态分布的统计特征, 多数钻孔反演的裂隙等效水力张开度随埋深呈指数形式衰减, 少数钻孔呈现出裂隙等效水力张开度随机性强、随埋深变化不明显的特征。相较传统方法, 本方法反演结果显著不同, 有待进一步验证。
- 裂隙岩体 /
- 裂隙张开度 /
- 离散裂隙网络模型 /
- 数值模拟 /
- 压水试验 /
- 三峡大坝
Abstract: Objective
The aperture of fractures (hydraulic equivalent aperture of fractures) of rock fractures is one of the key mechanical parameters of rocks.It has significant indicative significance in water conservancy projects, geological surveys and so on.At present, large-scale test methods such as cross-hole tests are often used to obtain the fracture apertures of deep rock masses in the field, but this method is rarely used many times in projects, and it is difficult to analyse the spatial variation in the aperture of fractures. This spatial variation is precisely what we need to focus on and discuss because it affects the accurate definition and application of the hydraulic equivalent fracture aperture in engineering applications.
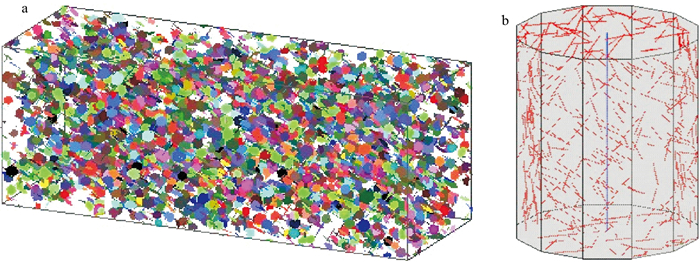
Methods
In this paper, taking the surrounding rock of an underground power station cavern on the right bank of the Three Gorges Dam as an example, a new inversion method for determining the hydraulic equivalent aperture of fractures is proposed by using conventional single-hole water injection test data and three-dimensional fracture network simulation. The statistical data obtained from the measured fracture cataloguing data are used to carry out random simulation of fracture characteristics, and a three-dimensional discrete fracture network seepage model connected with water injection test boreholes is constructed to fit the relationship between the single-hole steady-state flow rate and injection. The hydraulic equivalent apertures of fractures at different depths of rocks are inverted.
Results
The results show that the hydraulic equivalent aperture of fractures in the research area is generally 0.07-0.30 mm, which confirms to the statistical characteristics of the log-normal distribution. Most of the inverted hydraulic equivalent apertures of fractures in boreholes decrease exponentially with burial depth, while a few boreholes show strong randomness of the hydraulic equivalent aperture of fractures and no obvious change with burial depth.
Conclusion
Compared to those of traditional methods, the inversion results of this approach are significantly different and require further verification.
- fracture rock mass /
- fractures aperture /
- discrete fracture network model /
- numerical simulation /
- water injection test /
- Three Gorges Dam
注释:

所有作者声明不存在利益冲突。

HTML全文

图 1 三维裂隙网络随机模型

a.大范围直角坐标系裂隙网络; b.裁剪压水试验钻孔附近棱柱体内裂隙网络

Figure 1. Three-dimensional stochastic fracture network

下载: 全尺寸图片幻灯片

图 2 3013主硐左壁裂隙编录图

Figure 2. Mapped fractures on the left wall of the 3013 main tunnel

下载: 全尺寸图片幻灯片

图 3 不同区段裂隙倾向倾角等密图

Figure 3. Fracture dip direction and dip angle isodense graph for different segments

下载: 全尺寸图片幻灯片

图 4 不同区段实测裂隙产状的施密特极点图

Figure 4. Schmidt net of measured fractures in each section

下载: 全尺寸图片幻灯片

图 5 各区段实测裂隙迹线长度频率分布图

Figure 5. Trace length frequency distribution histogram of measured fractures in each section

下载: 全尺寸图片幻灯片

图 6 岩体透水率随试段埋深的变化

Figure 6. Variation in the rock mass permeability with the burial depth of the test section

下载: 全尺寸图片幻灯片

图 7 利用式(7)反算的裂隙等效水力张开度随埋深的变化

Figure 7. Variation in the equivalent hydraulic aperture of fractures with burial depth was calculated via the inverse method(7)

下载: 全尺寸图片幻灯片

图 8 某试段20次压水试验流量

Figure 8. Flow rate of 20 injection water tests in a test section

下载: 全尺寸图片幻灯片

图 9 张开度的频率分布柱状图及拟合曲线

Figure 9. Frequency distribution histogram and fitting curve of the equivalent hydraulic aperture of fractures

下载: 全尺寸图片幻灯片

图 10 多组裂隙平均等效水力张开度随试段埋深的变化

Figure 10. Average equivalent hydraulic aperture of fractures of multiple fractures changes with the burial depth of the test section

下载: 全尺寸图片幻灯片

表 1 各区段裂隙一维密度统计结果

Table 1. One-dimensional density calculation results for the fractures in each section

区段编号	初始测距/m	终止测距/m	一维密度/m^-1
A	0	35	1.06
B	35	170	1.14
C	170	235	1.03
D	235	360	0.85

下载: 导出CSV

表 2 各区段实测裂隙统计特征

Table 2. Statistical characteristics of the measured fractures in each section

区段	裂隙组	平均倾向/(°)	平均倾角/(°)	Fish分布K值	迹长均值/m	迹长标准差/m	一维密度/m^-1
A	1	85.5	36.6	15.8	2.05	0.43	0.31
	2	172.5	89.5	28.2	1.67	0.34	0.57
	3	291.7	58.7	14.1	2.78	0.75	0.17
B	1	107.1	38.7	7.7	1.58	0.84	0.41
	2	242.9	70.6	6.8	1.39	0.54	0.37
	3	355.3	69.2	8.3	1.54	0.80	0.33
C	1	29.4	72.4	5.9	1.56	0.48	0.38
	2	110.5	30.2	14.6	2.70	1.46	0.45
	3	285.9	64.5	6.1	1.58	0.98	0.20
D	1	100.3	46.7	10.0	2.25	0.87	0.32
	2	235.3	38.1	6.8	2.13	0.97	0.27
	3	347.1	72.7	5.7	2.16	1.22	0.26

下载: 导出CSV

表 3 各区段模拟裂隙统计特征

Table 3. Statistical characteristics of the simulated fractures in each section

区段	裂隙组	迹长均值/m	迹长标准差/m	三维密度/m^-3	直径均值/m	直径标准差/m
	1	1.89	0.39	0.17	1.92	0.27
A	2	1.61	0.30	0.24	1.82	0.38
	3	2.76	0.52	0.03	2.42	0.34
	1	1.62	1.08	0.06	1.73	1.06
B	2	1.39	0.57	0.30	1.59	0.62
	3	1.48	0.83	0.09	1.68	0.69
	1	1.74	0.70	0.32	1.53	0.47
C	2	2.97	1.47	0.04	2.23	1.07
	3	1.60	0.86	0.24	1.41	0.66
	1	2.60	0.87	0.06	2.09	0.72
D	2	2.46	0.95	0.14	2.02	0.90
	3	3.50	1.14	0.01	2.65	1.48

下载: 导出CSV

表 4 裂隙网络模拟反演的等效水力张开度均值

Table 4. Mean equivalent hydraulic aperture of fractures inversely estimated from fracture-network simulation

区段		A	B	C	D
区段		张开度均值/mm
裂隙组	1	0.195	0.108	0.113	0.081
	2	0.202	0.112	0.112	0.078
	3	0.201	0.104	0.110	0.083

下载: 导出CSV

参考文献(28)

[1]	王利, 孟兵兵, 曹运兴, 等. 水力压裂体积张开度模型[J]. 岩石力学与工程学报, 2020, 39(5): 887-900. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202005004.htm WANG L, MENG B B, CAO Y X, et al. A volumetric opening model of hydraulic fracturing[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(5): 887-900. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202005004.htm
[2]	刘世奇, 王鹤, 王冉, 等, 煤层孔隙与裂隙特征的研究进展[J]. 沉积学报, 2021, 39(1): 212-230. https://www.cnki.com.cn/Article/CJFDTOTAL-CJXB202101015.htm LIU S Q, WANG H, WANG R, et al. Research advances on characteristics of pores and fractures in coal seams[J]. Acta Sedimentologica Sinica, 2021, 39(1): 212-230. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-CJXB202101015.htm
[3]	SONG F, DONG Y H, XU Z F, et al. Granite microcracks: Structure and connectivity at different depths[J]. Journal of Asian Earth Sciences, 2016, 124: 156-168 doi: 10.1016/j.jseaes.2016.04.023
[4]	YU H C, YU H C, WANG G Q, et al. Experimental study on the effect of prefabricated fissures on the creep mechanical properties and acoustic emission characteristics of sandstone under uniaxial compression[J]. Frontiers in Earth Science, 2022, 10: 107-115.
[5]	WANG Z H, XU C S, PETER D. A modified cubic law for single-phase saturated laminar flow in rough rockfractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 103: 107-115. doi: 10.1016/j.ijrmms.2017.12.002
[6]	黄帆, 姚池, 周创兵, 等. 考虑裂隙迹长和开度相关性的随机裂隙网络数值模拟及渗流分析[J]. 水利水运工程学报, 2018(2): 35-42. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY201802005.htm HUANG F, YAO C, ZHOU C B, et al. Numerical simulation and seepage analysis of stochastic fracture network considering correlation between fracture trace length and aperture[J]. Hydro-Science and Engineering, 2018(2): 35-42. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY201802005.htm
[7]	胡成, 陈刚, 曹孟雄, 等. 基于离散裂隙网络法和水流数值模拟技术的地下水封洞库水封性研究[J]. 地质科技通报, 2022, 41(1): 119-126. 10.19509/j.cnki.dzkq.2022.0029 HU C, CHEN G, CAO M X, et al. Case study on water sealing efficiency of ground water storage caverns using disconcrete fracture network method and flow numerical simulation[J]. Bulletin of Geological Science and Technology, 2022, 41(1): 119-126. (in Chinesewith English abstract) 10.19509/j.cnki.dzkq.2022.0029
[8]	何忱, 姚池, 杨建华, 等. 基于等效离散裂隙网络的三维裂隙岩体渗流模型[J]. 岩石力学与工程学报, 2019, 38(增刊1): 2748-2759. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2019S1015.htm HE C, YAO C, YANG J H, et al. A 3D model for flow in fractured rock mass based on the equivalent discrete fracture network[J]. Chinese Journal of Rock Mechanics and Rock Mechanics and Engineering, 2019, 38(S1): 2748-2759. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2019S1015.htm
[9]	成建梅, 罗一鸣. 岩溶多重介质地下水模拟技术及应用进展[J]. 地质科技通报, 2022, 41(5): 220-229. doi: 10.19509/j.cnki.dzkq.2022.0220 CHENG J M, LUO Y M. Overview of groundwater modeling technology and its application in karst areas with multiplevoid media[J]. Bulletin of Geological Science and Technology, 2022, 41(5): 220-229. (in Chinese with English abstract) doi: 10.19509/j.cnki.dzkq.2022.0220
[10]	夏露, 谢娟, 于青春. 裂隙延展性统计分布离散性对岩体块体化程度REV的影响[J]. 水文地质工程地质, 2019, 46(4): 112-118. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201904016.htm XIA L, XIE J, YU Q C. Influence of statistical distribution dispersion in the fracture size on blockiness REV of fractured rock masses[J]. Hydrogeology & Engineering Geology, 2019, 46(4): 112-118. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201904016.htm
[11]	于青春, 陈德基, 薛果夫, 等. 裂隙岩体一般块体理论初步[J]. 水文地质工程地质, 2005, 32(6): 42-48. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG200506010.htm YU Q C, CHEN D J, XUE G F, et al. Preliminary study on general block method of fractured rock mass[J]. Hydrogeology & Engineering Geology, 2005, 32(6): 42-48. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG200506010.htm
[12]	MAXIMILIAN O, KOTTWITZ, ANTON A, et al. The hydraulic efficiency of single fractures: Correcting the cubic law parameterization for self-affine surface roughness and fracture closure[J]. Solid Earth, 2020, 11(3): 947-957.
[13]	LU Y Y, CHEN X Y, LI H L, et al. An improved cubic law for shale fracture considering the effect of loading path[J]. International Journal of Oil, Gas and Coal Technology, 2021, 26(1): 25-26.
[14]	ZHANG W J, PENG Z Y, HAN C H, et al. Numerical investigation of an equivalent hydraulic aperture for rough rock fractures based on cosimulation[J]. Computers and Geotechnics, 2023, 156: 105281.
[15]	BEAR J. Dynamics of fluids in porous media[M]. New York: Elsevier, 1972.
[16]	DAVID T S. An isotropic permeability of fractured media[J]. Water Resources Research, 1969, 5(12): 1273-1289.
[17]	于青春, 大西有三. 岩体三维不连续裂隙网络及其逆建模方法[J]. 地球科学, 2003, 28(5): 522-527. https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX200305008.htm YU Q C, OHNISHI Y Z. Three-dimensional discrete fracture network model and its inverse method[J]. Earth Science, 2003, 28(5): 522-526. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-DQKX200305008.htm
[18]	U.S. Committee for Rock Mechanics. Rock fracture and fluidflow: Contemporary understanding and applications[S]. Washington D.C. : National Academy Press, 1996.
[19]	KULATILAKE P H S, WANG W S, STEPHANSSON O. Effect of finite size joints on the deformability of jointed rock in three dimensions[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1993, 30(5): 479-501.
[20]	于青春, 刘丰收, 大西有三. 岩体非连续裂隙网络三维面状渗流模型[J]. 岩石力学与工程学报, 2005, 24(4): 662-668. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200504021.htm YU Q C, LIU F S, OHNISHI Y Z. Three-dimensional planar model for fluid flow in discrete fracture network of rock masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(4): 662-668. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200504021.htm
[21]	HE X P, SINAN M, KWAK H, et al. A corrected cu-bic law for single-phase laminar flow through rough-walled fractures[J]. Advances in Water Resources, 2021, 154: 103984.
[22]	YU Q. Analyses for fluid flow and solute transport in discrete fracture network[D]. Kyoto: Kyoto University, 2000.
[23]	Lugeon M. Barrages et géologie, méthodes de recherches: Terrassement et imperméabilisation[M]. Lausanne: Rouge, 1933.
[24]	陈崇希. Dupuit圆岛稳定井流模型的改进: 具入渗补给[J]. 水文地质工程地质, 2020, 47(5): 1-4. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG202106001.htm CHEN C X. Improvement of Dupuit model: With infiltration recharge[J]. Hydrogeology & Engineering Geology, 2020, 47(5): 1-4. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG202106001.htm
[25]	ZHOU J Q, CHEN Y F, TANG H M, et al. Disentangling the simultaneous effects of inertial losses and fracture dilation on permeability of pressurized fractured rocks (Article)[J]. Geophysical Research Letters, 2019, 46(15): 8862-8871.
[26]	张莉丽, 于青春, 王允, 等. 三峡工程地下电站主厂房围岩渗透性研究[J]. 地学前缘, 2010, (6): 286-290. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY201006040.htm ZHANG L L, YU Q C, WANG Y, et al. Permeability of the rock mass around the underground powerhouse of Three Gorges Project[J]. Earth Science Frontiers, 2010, 17(6): 286-290. (in Chinese with English abstract) https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY201006040.htm
[27]	MARDIA K V. Statistics of directional data[M]. Lon-don: Academic Press Inc., 1972.
[28]	朱建业. 《水利水电工程地质勘察规范》(GB 50287-99)[S]. 北京: 水利部水利水电规划设计总院, 2004. ZHU J Y. Code for water resources and hydropower engineering geological investigation (GB 50287-99)[S]. Beijing: General Institute of Water Conservancy and Hydropower Planning and Design, Ministry of Water Resources, 2004.