Research progress on coastal groundwater flow and solute transport processes based on MARUN
-
摘要:
为定量研究海岸带众多非线性因素对含水层中地下水流-溶质运移过程的影响, MARUN(Marine Unsaturated) 这款专门用于海岸带地下水数值模拟的软件被开发完成。从模型原理、算法特点、文献调研、案例分析等方面综述了MARUN的研究和应用进展。该软件适用于海岸带二维垂直剖面的地下水流及溶质运移反应的数值模拟。MARUN实现了变密度、变饱和度渗流与溶质运移的有限元算法, 质量集中的隐式差分离散, 以及Picard、Newton、Newton-Picard数值解法, 涵盖了海潮海浪、蒸发降雨和荷载效应等众多非线性因素, 具有专业性强、灵活性好、容错率高等特点, 但没有可视化界面。MARUN已在原油污染的海滩生物修复、潮间带浅层含水层海水-地下水循环过程、区域地下水流系统的演化等场景中取得一批富有特色的研究成果。未来, MARUN需要进一步拓展到三维空间, 耦合具有随机特征的物理化学过程, 以提高对滨海含水层中地下水流与溶质运移过程的模拟仿真水平。
Abstract:Sgnificance To quantitatively study the impact of various nonlinear factors in the coastal zone on groundwater flow and solute transport processes, MARUN (Marine Unsaturated) software for simulating groundwater flow in the coastal zone was developed.
Progress This paper reviews the research and application progress of MARUN from the aspects of model principles, algorithm characteristics, literature review, and case analyses. The software is suitable for numerical simulations of two-dimensional vertical profiles of groundwater flow and solute transport reactions in the coastal zone. MARUN implements a finite element algorithm for variable saturation and density flow and solute transport, mass-consistent implicit difference discretization, and Picard, Newton, and Newton-Picard numerical solution methods, covering many nonlinear factors such as tides, waves, evaporation, rainfall, and load effects. It is characterized by its high professionalism, good flexibility, and high fault tolerance, but it does not have a graphical user interface. MARUN has achieved a number of highlighted research results in scenarios such as bioremediation of crude oil pollution on beaches, seawater-groundwater circulation processes in shallow aquifers in intertidal zones, and the evolution of regional groundwater flow systems.
Conclusion and Prospects In the future, MARUN needs to be further expanded into three-dimensional space and coupled with physicochemical processes with random characteristics to improve its performance level of simulating groundwater flow and solute transport in coastal aquifers.
-
Key words:
- coastal zone /
- groundwater /
- numerical simulation /
- MARUN
-
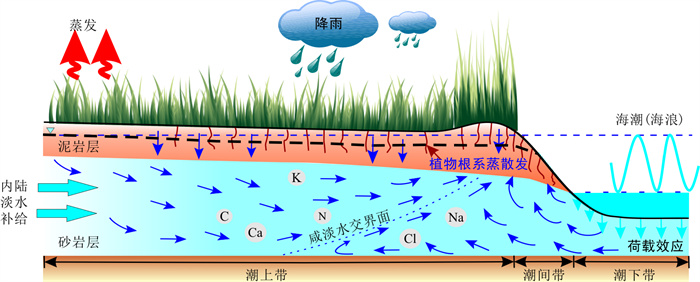
图 1 滨海含水层地下水流及溶质运移过程的概念模型(改自文献[27])
Figure 1. Scheme of the groundwater flow and solute transport in the coastal aquifer
图 3 利用MARUN再现的盐楔与淡水排泄通道(改自文献[53])
Figure 3. Salt wedges and freshwater discharge tube reproduced by MARUN
图 4 美国阿拉斯加海湾研究区(a), 石油污染物滞留的MARUN模型(b)及溢油滞留机理的阐述(c)(改自文献[56])
Figure 4. Alaska Gulf research area in United States (a), MARUN model of oil pollutant retention (b) and explanation of oil spill retention mechanism (c)
图 5 无量纲化的海滩剖面模型(改自文献[88])
Figure 5. A dimensionless beach profile model
表 1 国内外主要的地下水数值模拟软件
Table 1. Groundwater simulation software at home and abroad
软件名称 功能 特点 资料来源 MODFLOW 模拟孔隙介质中三维地下水流动及溶质运移过程 有限差分离散;具有模块化结构 文献[14] MT3DMS 模拟地下水流系统中的三维溶质迁移和简单化学反应过程 有限差分离散;支持模拟结果的可视化和后处理;与其他软件的耦合性强;处理复杂反应的能力不足;忽略了溶质运移引起的密度变化 文献[15] SEAWAT 模拟变密度的三维地下水流动及溶质和热运移过程 耦合了MODFLOW和MT3DMS;不能处理非饱和带地下水流问题 文献[17] PHREEQC 模拟多种复杂低温地球化学反应过程 强大的地球化学反应系统;支持与多种软件的耦合 文献[22] PHT3D 模拟三维平流-弥散多组分输运和生物地球化学反应过程 耦合了MT3DMS和PHREEQC;输入文件复杂;不能处理非饱和系统的反应性传输;地下水流的问题必须提前用外置软件(通常是MODFLOW)来解决 文献[16] GMS 模拟孔隙介质中的二维和三维地下水流动、溶质运移-反应过程 有限元、有限差分和有限体积离散;与MODFLOW,MT3DMS,PHT3D,SEAWAT等耦合;操作界面友好;前、后处理功能强大;具有完善的自检查功能 文献[18] FEFLOW 模拟多孔、裂隙介质中变饱和-变密度的二维和三维地下水流动、溶质和热运移过程 有限元离散;主要针对裂隙、断层、弱透水带等复杂地层条件;具有丰富实用的图形显示和数据结果分析工具 文献[19-20] SUTRA 模拟变饱和-变密度的二维和三维地下水流动、溶质(含吸附和衰变)和热运移过程 有限元和有限差分离散;网格剖分灵活;包含了河流、排水沟、蒸散等水文过程对模型的影响;具有通用的数值原理和程序结构 文献[21] TOUGH2/TOUGHREACT 模拟多孔、裂隙介质中二维和三维的多组分、多相非等温流体的运移和反应过程 有限差分离散;包含了气体溶解和排出、阳离子交换、水的络合反应、矿物的溶解和沉淀等多种化学过程 文献[23] HydroGeoSphere 模拟多孔、裂隙介质中区域地下水流动、溶质和热运移过程 控制体积的有限元离散;地表-地下水流系统的耦合;图形界面友好;用户操作简单;前、后处理功能强大 文献[24] 表 2 运用MARUN完成数值模拟研究的代表性文献综述
Table 2. A literature review of representative studies on numerical simulation conducted based on the MARUN model
序号 研究问题或模型特色 模型形状 地下水特性 含水层特性 典型边界条件 主要发现或结论 研究类别 资料来源 变饱和度 变密度 非均质性 各向异性 1 变饱和度 B √ - - - 海潮 模型首次考虑变饱和度作用,发现流场模拟结果对VG模型参数α的敏感度高于n Ⅱ 文献[26] 2 变密度 B √ √ - - 海潮 首次报道了海潮作用下海滩含水层中盐楔以及淡水排泄通道的存在 Ⅱ 文献[53] 3 各向异性 B √ √ - √ - 含水层的各向异性,会导致咸淡水界面向海移动,减小海水入侵的范围 Ⅰ 文献[54] 4 随机分形非均质性 B √ √ H √ 海潮 随机分形非均质极大改变了上盐羽的时空演化过程,导致局部孔隙水流速度增大,海滩表层出现瞬态优先流,演化出多个局部地下水循环单元及盐指 Ⅰ 文献[55] 5 分层非均质性 B √ √ S - 海潮 分层非均质会显著改变地下水流场,使得表层和底层出现明显的分带,诱导海水-地下水循环过程发生在高渗透层,盐分(或营养物)滞留在低渗透层 Ⅲ 文献[56] 6 海潮荷载效应 R - √ - - 海潮 海潮引起的荷载效应会增强近岸地下水的波动,减小海水与孔隙水的水力梯度;荷载作用越强,海水与孔隙水的波动就越同步,海底地下水排泄通量就越少 Ⅰ 文献[57] 7 海浪效应 B √ √ - - 海潮海浪 海浪作用增加了海底地下水交换通量,并在海滩表面产生了更宽的交换区,同时显著增加了上盐羽的分布范围 Ⅱ 文献[58] 8 蒸发作用 B √ √ - - 海潮蒸发 在相对潮湿的大气条件下,最大蒸发区域发生在潮间带;而当大气条件恒定且有利于蒸发(高温和低空气湿度)时,最大蒸发区域才向潮上带转移 Ⅲ 文献[59] 9 降雨作用 B √ √ - - 降雨蒸发 蒸发作用会显著增加孔隙水盐度,在地表形成高盐羽区和局部地下水循环单元;降雨补给会稀释表层高盐羽区,使盐分向下迁移,最终增加海底地下水排泄通量 Ⅲ 文献[60] 10 蒸散发作用 B √ - S √ 蒸散 从饱和-不饱和含水层条件以及地下水-河水交换速率两方面分析了植物分带的原因 Ⅲ 文献[31] 11 地层演化过程 RS √ √ S √ 海侵海退 首次完成了区域性尺度的地下水流模拟,再现了全新世珠江三角洲区域地下水流系统的演化过程 Ⅲ 文献[61] 注:对于模型形状,B表示带一定坡度的典型海滩剖面(图 1),R表示矩形剖面,RS表示区域尺度的地层剖面;对于含水层非均质性特征,S表示分层非均质性,H表示随机分形非均质性;“√”表示模型考虑的特性,“-”表示没有考虑的特性 -
[1] Beatley T, Brower D, Schwab A K. An introduction to coastal zone management[M]. Washington: Island Press, 2002. [2] Dominguez J M L. The coastal zone of Brazil: An overview[J]. Journal of Coastal Research, 2006, 39(1): 16-20. [3] Sun Z, Sun W, Tong C, et al. China's coastal wetlands: Conservation history, implementation efforts, existing issues and strategies for future improvement[J]. Environment International, 2015, 79: 25-41. doi: 10.1016/j.envint.2015.02.017 [4] Howarth R W. Coastal nitrogen pollution: A review of sources and trends globally and regionally[J]. Harmful Algae, 2008, 8(1): 14-20. doi: 10.1016/j.hal.2008.08.015 [5] Santos I R, Chen X, Lecher A L, et al. Submarine groundwater discharge impacts on coastal nutrient biogeochemistry[J]. Nature Reviews Earth & Environment, 2021, 2(5): 307-323. [6] Jiang T T, Pan J F, Pu X M, et al. Current status of coastal wetlands in China: Degradation, restoration, and future management[J]. Estuarine, Coastal and Shelf Science, 2015, 164: 265-275. doi: 10.1016/j.ecss.2015.07.046 [7] Zhang Y, Li H, Wang X, et al. Estimation of submarine groundwater discharge and associated nutrient fluxes in eastern Laizhou Bay, China using 222Rn[J]. Journal of Hydrology, 2016, 533: 103-113. doi: 10.1016/j.jhydrol.2015.11.027 [8] Kang Y, Liu Q, Cheng Y, et al. Combined freeze-sealing and New Tubular Roof construction methods for seaside urban tunnel in soft ground[J]. Tunnelling and Underground Space Technology, 2016, 58: 1-10. doi: 10.1016/j.tust.2016.04.001 [9] 王焰新, 甘义群, 邓娅敏, 等. 海岸带海陆交互作用过程及其生态环境效应研究进展[J]. 地质科技通报, 2020, 39(1): 1-10. doi: 10.19509/j.cnki.dzkq.2020.0101Wang Y X, Gan Y Q, Deng Y M, et al. Land-ocean interactions, and their eco-environmental effects in the coastal zone: Current progress and future perspectives[J]. Bulletin of Geological Science and Technology, 2020, 39(1): 1-10 (in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0101 [10] 易泽邦, 刘千红, 曹建劲, 等. 广州珠江三角洲海水入侵地区地下水微粒的TEM分析及意义[J]. 地质科技情报, 2015, 34(4): 194-199. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201504029.htmYi Z B, Liu Q H, Cao J J, et al. TEM analysis of groundwater microparticles in the Pearl River Delta of Guangzhou and its significance[J]. Geological Science and Technology Information, 2015, 34(4): 194-199 (in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ201504029.htm [11] Anderson M, Woessner W, Hunt R. Applied groundwater modeling: Simulation of flow and advective transport[J]. Journal of Hydrology, 1992, 140: 393-395. doi: 10.1016/0022-1694(92)90251-P [12] Anderson M P, Woessner W W, Hunt R J. Applied groundwater modeling: Simulation of flow and advective transport[M]. Amsterdam: Elsevier Press, 2015. [13] Kresic N. Hydrogeology and groundwater modeling[M]. Boca Raton: CRC Press, 2006. [14] Harbaugh A W, Banta E R, Hill M C, et al. MODFLOW-2000, The U.S. Geological survey modular ground-water model-user guide to modularization concepts and the ground-water flow process[M]. Colorado: U.S. Geological Survey, 2000. [15] Zheng C C, Hill M, Cao G, et al. MT3DMS: Model use, calibration, and validation[J]. Transactions of the ASABE, 2012, 55(4): 1549-1559. doi: 10.13031/2013.42263 [16] Appelo C A J, Rolle M. PHT3D: A reactive multicomponent transport model for saturated porous media[J]. Groundwater, 2010, 48(5): 627-632. doi: 10.1111/j.1745-6584.2010.00732.x [17] Langevin C D. User's guide to SEAWAT: A computer program for simulation of three-dimensional variable-density groundwater flow[R]. Techniques of Water-Resources Investigations 6-A7. Tallahassee: U.S. Geological Survey, 2002. [18] Xiao B Z. The software (GMS) of groundwater modeling system[J]. Hydrogeology and Engineering Geology, 2003, 5: 53-55. [19] Trefry M G, Muffels C. FEFLOW: A finite-element ground water flow and transport modeling tool[J]. Groundwater, 2007, 45(5): 525-528. doi: 10.1111/j.1745-6584.2007.00358.x [20] Diersch H J G. FEFLOW: Finite element modeling of flow, mass and heat transport in porous and fractured media[M]. Berlin: Springer Press, 2014. [21] Provost A M, Voss C I. SUTRA, a model for saturated-unsaturated, variable-density groundwater flow with solute or energy transport: Documentation of generalized boundary conditions, a modified implementation of specified pressures and concentrations or temperatures, and the lake capability[R]. Techniques and Methods 6-A52, Reston: U.S. Geological Survey, 2019. [22] Parkhurst D L, Appelo C A J. Description of input and examples for PHREEQC version 3: A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations[R]. Techniques and Methods 6-A43, Denver: U.S. Geological Survey, 2013. [23] Croucher A E, O'Sullivan M J. Application of the computer code TOUGH2 to the simulation of supercritical conditions in geothermal systems[J]. Geothermics, 2008, 37(6): 622-634. doi: 10.1016/j.geothermics.2008.03.005 [24] Brunner P, Simmons C T. HydroGeoSphere: A fully integrated, physically based hydrological model[J]. Groundwater, 2012, 50(2): 170-176. doi: 10.1111/j.1745-6584.2011.00882.x [25] Boufadel M C. Nutrient transport in beaches: Effect of tides, waves, and buoyancy[D]. Cincinnati: University of Cincinnati, 1998. [26] Boufadel M C, Suidan M T, Venosa A D. A numerical model for density-and-viscosity-dependent flows in two-dimensional variably saturated porous media[J]. Journal of Contaminant Hydrology, 1999, 37(1/2): 1-20. [27] Xiao K, Wilson A M, Li H, et al. Crab burrows as preferential flow conduits for groundwater flow and transport in salt marshes: A modeling study[J]. Advances in Water Resources, 2019, 132: 103408. doi: 10.1016/j.advwatres.2019.103408 [28] Van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. doi: 10.2136/sssaj1980.03615995004400050002x [29] Van Der Kamp G, Gale J E. Theory of earth tide and barometric effects in porous formations with compressible grains[J]. Water Resources Research, 1983, 19(2): 538-544. doi: 10.1029/WR019i002p00538 [30] Li H, Li L, Lockington D. Aeration for plant root respiration in a tidal marsh[J]. Water Resources Research, 2005, 41(6): W06023. [31] Xiao K, Li H, Wilson A M, et al. Tidal groundwater flow and its ecological effects in a brackish marsh at the mouth of a large sub-tropical river[J]. Journal of Hydrology, 2017, 555: 198-212. doi: 10.1016/j.jhydrol.2017.10.025 [32] Spiteri C, Cappellen P V, Regnier P. Surface complexation effects on phosphate adsorption to ferric iron oxyhydroxides along pH and salinity gradients in estuaries and coastal aquifers[J]. Geochimica et Cosmochimica Acta, 2008, 72(14): 3431-3445. doi: 10.1016/j.gca.2008.05.003 [33] Spiteri C, Slomp C P, Charette M A, et al. Flow and nutrient dynamics in a subterranean estuary (Waquoit Bay, MA, USA): Field data and reactive transport modeling[J]. Geochimica et Cosmochimica Acta, 2008, 72(14): 3398-3412. doi: 10.1016/j.gca.2008.04.027 [34] Spiteri C, Slomp C P, Tuncay K, et al. Modeling biogeochemical processes in subterranean estuaries: Effect of flow dynamics and redox conditions on submarine groundwater discharge of nutrients[J]. Water Resources Research, 2008, 44(2): W02430. [35] Cooley R L. Some new procedures for numerical solution of variably saturated flow problems[J]. Water Resources Research, 1983, 19(5): 1271-1285. doi: 10.1029/WR019i005p01271 [36] Neuman S P. Saturated-unsaturated seepage by finite elements[J]. Journal of the Hydraulics Division, 1973, 99(12): 2233-2250. doi: 10.1061/JYCEAJ.0003829 [37] Huyakorn P S, Thomas S D, Thompson B M. Techniques for making finite elements competitve in modeling flow in variably saturated porous media[J]. Water Resources Research, 1984, 20(8): 1099-1115. doi: 10.1029/WR020i008p01099 [38] Huyakorn P S, Springer E P, Guvanasen V, et al. A three-dimensional finite-element model for simulating water flow in variably saturated porous media[J]. Water Resources Research, 1986, 22(13): 1790-1808. doi: 10.1029/WR022i013p01790 [39] Gureghian A B. TRIPM: Two-dimensional finite-element model for the simultaneous transport of water and reacting solutes through saturated and unsaturated porous media: Technical report[R]. [S. l. ]: Battelle Memorial Institute, Office of Nuclear Waste Isolation, 1983. [40] Voss C I. A finite-element simulation model for saturated-unsaturated, fluid-density-dependent ground-water flow with energy transport or chemically-reactive single-species solute transport[R]. Water-Resources Invectigations Report 84-4389, Reston: U.S. Geological Survey, 1984. [41] Anderson D, Tannehill J C, Pletcher R H. Computational fluid mechanics and heat transfer[M]. Boca Raton: CRC Press, 2012. [42] Celia M A, Bouloutas E T, Zarba R L. A general mass-conservative numerical solution for the unsaturated flow equation[J]. Water Resources Research, 1990, 26(7): 1483-1496. doi: 10.1029/WR026i007p01483 [43] Gureghian A B. A two-dimensional finite-element solution for the simultaneous transport of water and nultisolutes trough a nonhomogeneous aquifer under transient saturted-unsaturated flow conditions[J]. Science of the Total Environment, 1981, 21: 329-337. doi: 10.1016/0048-9697(81)90166-2 [44] Kinzelbach W. Groundwater modelling: An introduction with sample programs in BASIC[M]. Ansterdan: Elsevier Press, 1986. [45] Huang K, Mohanty B P, vanGenuchten M T. A new convergence criterion for the modified Picard iteration method to solve the variably saturated flow equation[J]. Journal of Hydrology, 1996, 178(1/4): 69-91. [46] Huang K, Mohanty B P, Leij F J, et al. Solution of the nonlinear transport equation using modified Picard iteration[J]. Advances in Water Resources, 1998, 21(3): 237-249. doi: 10.1016/S0309-1708(96)00046-2 [47] Paniconi C, Putti M. A comparison of Picard and Newton iteration in the numerical solution of multidimensional variably saturated flow problems[J]. Water Resources Research, 1994, 30(12): 3357-3374. doi: 10.1029/94WR02046 [48] Putti M, Paniconi C. Picard and Newton linearization for the coupled model for saltwater intrusion in aquifers[J]. Advances in Water Resources, 1995, 18(3): 159-170. doi: 10.1016/0309-1708(95)00006-5 [49] Bergamaschi L, Putti M. Mixed finite elements and Newton-type linearizations for the solution of Richards' equation[J]. International Journal for Numerical Methods in Engineering, 1999, 45(8): 1025-1046. doi: 10.1002/(SICI)1097-0207(19990720)45:8<1025::AID-NME615>3.0.CO;2-G [50] Maurer D, Wieners C. A parallel block LU decomposition method for distributed finite element matrices[J]. Parallel Computing, 2011, 37(12): 742-758. doi: 10.1016/j.parco.2011.05.007 [51] Koniges A E, Anderson D V. ILUBCG2: A preconditioned biconjugate gradient routine for the solution of linear asymmetric matrix equations arising from 9-point discretizations[J]. Computer Physics Communications, 1987, 43(2): 297-302. doi: 10.1016/0010-4655(87)90213-X [52] Wang W, Dai Z, Li J, et al. A hybrid Laplace transform finite analytic method for solving transport problems with large Peclet and Courant numbers[J]. Computers & Geosciences, 2012, 49: 182-189. [53] Boufadel M C. A mechanistic study of nonlinear solute transport in a groundwater-surface water system under steady state and transient hydraulic conditions[J]. Water Resources Research, 2000, 36(9): 2549-2565. doi: 10.1029/2000WR900159 [54] Qu W, Li H, Wan L, et al. Numerical simulations of steady-state salinity distribution and submarine groundwater discharges in homogeneous anisotropic coastal aquifers[J]. Advances in Water Resources, 2014, 74: 318-328. doi: 10.1016/j.advwatres.2014.10.009 [55] Geng X, Boufadel M C, Rajaram H, et al. Numerical study of solute transport in heterogeneous beach aquifers subjected to tides[J]. Water Resources Research, 2020, 56(3): e2019WR026430. [56] Li H, Boufadel M C. Long-term persistence of oil from the Exxon Valdez spill in two-layer beaches[J]. Nature Geoscience, 2010, 3(2): 96-99. doi: 10.1038/ngeo749 [57] Wang X, Li H, Wan L, et al. Loading effect of water table variation and density effect on tidal head fluctuations in a coastal aquifer system[J]. Water Resources Research, 2012, 48(9): W09501. [58] Geng X, Boufadel M C, Xia Y, et al. Numerical study of wave effects on groundwater flow and solute transport in a laboratory beach[J]. Journal of Contaminant Hydrology, 2014, 165: 37-52. doi: 10.1016/j.jconhyd.2014.07.001 [59] Geng X, Boufadel M C. Impacts of evaporation on subsurface flow and salt accumulation in a tidally influenced beach[J]. Water Resources Research, 2015, 51(7): 5547-5565. doi: 10.1002/2015WR016886 [60] Geng X, Boufadel M C. The influence of evaporation and rainfall on supratidal groundwater dynamics and salinity structure in a sandy beach[J]. Water Resources Research, 2017, 53(7): 6218-6238. doi: 10.1002/2016WR020344 [61] Yu S, Jiao J J, Luo X, et al. Evolutionary history of the groundwater system in the Pearl River Delta during the Holocene[J]. Geology, 2023, 51(5): 481-485. doi: 10.1130/G50888.1 [62] Boufadel M C, Suidan M T, Venosa A D. Density-dependent flow in one-dimensional variably-saturated media[J]. Journal of Hydrology, 1997, 202(1/4): 280-301. [63] Boufadel M C, Suidan M T, Venosa A D, et al. 2D variably saturated flows: Physical scaling and Bayesian estimation[J]. Journal of Hydrologic Engineering, 1998, 3(4): 223-231. doi: 10.1061/(ASCE)1084-0699(1998)3:4(223) [64] Boufadel M C, Suidan M T, Venosa A D, et al. Steady seepage in trenches and dams: Effect of capillary flow[J]. Journal of Hydraulic Engineering, 1999, 125(3): 286-294. doi: 10.1061/(ASCE)0733-9429(1999)125:3(286) [65] Boufadel M, Suidan M, Venosa A. Numerical modeling of water flow below dry salt lakes: Effect of capillarity and viscosity[J]. Journal of Hydrology, 1999, 221(1/2): 55-74. [66] Li H, Zhao Q, Boufadel M C, et al. A universal nutrient application strategy for the bioremediation of oil-polluted beaches[J]. Marine Pollution Bulletin, 2007, 54(8): 1146-1161. doi: 10.1016/j.marpolbul.2007.04.015 [67] Li H, Boufadel M C, Weaver J W. Quantifying bank storage of variably saturated aquifers[J]. Groundwater, 2008, 46(6): 841-850. [68] Guo Q, Li H, Zhou Z, et al. Rainfall infiltration-derived submarine groundwater discharge from multi-layered aquifer system terminating at the coastline[J]. Hydrological Processes, 2012, 26(7): 985-995. doi: 10.1002/hyp.8188 [69] Geng X, Boufadel M C. Numerical modeling of water flow and salt transport in bare saline soil subjected to evaporation[J]. Journal of Hydrology, 2015, 524: 427-438. doi: 10.1016/j.jhydrol.2015.02.046 [70] Abdollahi-Nasab A, Boufadel M C, Li H, et al. Saltwater flushing by freshwater in a laboratory beach[J]. Journal of Hydrology, 2010, 386(1/4): 1-12. [71] Boufadel M C, Xia Y, Li H. Modeling solute transport and transient seepage in a laboratory beach under tidal influence[J]. Environmental Modelling & Software, 2011, 26(7): 899-912. [72] Geng X, Boufadel M C, Lee K, et al. Biodegradation of subsurface oil in a tidally influenced sand beach: Impact of hydraulics and interaction with pore water chemistry[J]. Water Resources Research, 2015, 51(5): 3193-3218. doi: 10.1002/2014WR016870 [73] Geng X, Boufadel M C. Numerical study of solute transport in shallow beach aquifers subjected to waves and tides[J]. Journal of Geophysical Research: Oceans, 2015, 120(2): 1409-1428. doi: 10.1002/2014JC010539 [74] Xia Y, Li H, Boufadel M C, et al. Hydrodynamic factors affecting the persistence of the Exxon Valdez oil in a shallow bedrock beach[J]. Water Resources Research, 2010, 46(10): W10528. [75] Guo Q, Li H, Boufadel M C, et al. Hydrodynamics in a gravel beach and its impact on the Exxon Valdez oil[J]. Journal of Geophysical Research: Oceans, 2010, 115(C12): C12077. [76] Li H, Boufadel M C. A tracer study in an Alaskan gravel beach and its implications on the persistence of the Exxon Valdez oil[J]. Marine Pollution Bulletin, 2011, 62(6): 1261-1269. doi: 10.1016/j.marpolbul.2011.03.011 [77] Guo Q, Li H, Boufadel M C, et al. A field experiment and numerical modeling of a tracer at a gravel beach in Prince William Sound, Alaska[J]. Hydrogeology Journal, 2014, 22(8): 1795-1805. doi: 10.1007/s10040-014-1184-3 [78] Geng X, Boufadel M, Abdollahi-Nasab A. Hydrodynamics in a sandy beach polluted with the Deepwater Horizon oil spill[C]//Patterson C L, Struck S D, Murray J D J. Proceedings of the world environmental and water resources congress. Reston: American Society of Civil Engineers, 2013: 460-467. [79] Geng X, Pan Z, Boufadel M C, et al. Simulation of oil bioremediation in a tidally influenced beach: Spatiotemporal evolution of nutrient and dissolved oxygen[J]. Journal of Geophysical Research: Oceans, 2016, 121(4): 2385-2404. doi: 10.1002/2015JC011221 [80] Geng X, Boufadel M C. Modeling biodegradation of subsurface oil in sand beaches polluted with oil[C]//Miller E J. Proceedings of the International Oil Spill Conference Proceedings of the international oil spill conference. Washington: American Petroleum Institute, 2014: 1113-1125. [81] Geng X, Boufadel M C, Jackson N L. Evidence of salt accumulation in beach intertidal zone due to evaporation[J]. Scientific Reports, 2016, 6(1): 1-5. doi: 10.1038/s41598-016-0001-8 [82] Geng X, Heiss J W, Michael H A, et al. Subsurface flow and moisture dynamics in response to swash motions: Effects of beach hydraulic conductivity and capillarity[J]. Water Resources Research, 2017, 53(12): 10317-10335. doi: 10.1002/2017WR021248 [83] Xiao K, Li H, Xia Y, et al. Effects of tidally varying salinity on groundwater flow and solute transport: insights from modelling an idealized creek marsh aquifer[J]. Water Resources Research, 2019, 55(11): 9656-9672. doi: 10.1029/2018WR024671 [84] Bragg J R, Prince R C, Harner E J, et al. Effectiveness of bioremediation for the Exxon Valdez oil spill[J]. Nature, 1994, 368(6470): 413-418. doi: 10.1038/368413a0 [85] Hayes M O, Michel J. Factors determining the long-term persistence of Exxon Valdez oil in gravel beaches[J]. Marine Pollution Bulletin, 1999, 38(2): 92-101. doi: 10.1016/S0025-326X(99)00099-5 [86] Short J W, Lindeberg M R, Harris P M, et al. Estimate of oil persisting on the beaches of prince william sound 12 years after the Exxon Valdez oil spill[J]. Environmental Science & Technology, 2004, 38(1): 19-25. [87] Short J W, Maselko J M, Lindeberg M R, et al. Vertical distribution and probability of encountering intertidal Exxon Valdez oil on shorelines of Three Embayments within Prince William Sound, Alaska[J]. Environmental Science & Technology, 2006, 40(12): 3723-3729. [88] Short J W, Irvine G V, Mann D H, et al. Slightly weathered Exxon Valdez oil persists in Gulf of Alaska beach sediments after 16 gears[J]. Environmental Science & Technology, 2007, 41(4): 1245-1250. [89] Yeh G T. On the computation of Darcian velocity and mass balance in the finite element modeling of groundwater flow[J]. Water Resources Research, 1981, 17(5): 1529-1534. [90] Neuman Shlomo P. Saturated-unsaturated seepage by finite elements[J]. Journal of the Hydraulics Division, 1973, 99(12): 2233-2250. [91] Naba B, Boufadel M C, Weaver J. The role of capillary forces in steady-state and transient seepage flows[J]. Groundwater, 2002, 40(4): 407-415. [92] Li H, Boufadel M C, Weaver J W. Tide-induced seawater–groundwater circulation in shallow beach aquifers[J]. Journal of Hydrology, 2008, 352(1/2): 211-224. [93] Massel S R. Hydrodynamics of coastal zones[M]. Amsterdam: Elsevier Press, 1989. [94] Wright L D, Short A D. Morphodynamic variability of surf zones and beaches: A synthesis[J]. Marine Geology, 1984, 56(1/4): 93-118. [95] Geng X, Heiss J W, Michael H A, et al. Geochemical fluxes in sandy beach aquifers: Modulation due to major physical stressors, geologic heterogeneity, and nearshore morphology[J]. Earth-Science Reviews, 2021, 221: 103800. -





 下载:
下载: