An improved method for determining the coefficient of resource scale variation (k) in reservoir size sequential analysis and its application case
-
摘要:
规模序列法基于Pareto定律，有效获取油气藏规模变化系数（
k ）的取值长期以来是该方法应用中的关键及难点，并制约了该方法的应用成效。通过求取已发现油气资源规模比，利用已发现油气资源可能具有的规模序列号，构建了一种对k 的优化取值技术，主要包括：以资源规模序列号与k 为坐标轴建立坐标系，根据已发现油气资源规模比做数据交汇，当不同规模比下的交汇数据点近似位于垂直于k 轴的直线上时，该直线与k 轴的交点即为k 的一个解；进一步提出了在获取k 及规模序列解集后，对解集进行优选定解的原则，以满足油气资源评价需求。对已发表文献中经典数据的分析表明，通过应用该技术可有效获取油气藏规模变化系数（k ）的取值；并进一步构建了对川中金秋气区盐亭区块侏罗系沙溪庙组6号砂组天然气资源的应用实例，表明预测与实际拟合结果较好，评价结果符合当前盆地天然气勘探认识。该技术对地质经验依赖程度低、不需要设定分析步长、无复杂的行列式-矩阵运算环节，有效降低了在k 取值过程中的主观性和计算强度，并实现了程序化，提高了分析时效性，可为规模序列法的深入应用提供帮助。-
关键词:
- 规模序列 /
- 油气藏规模变化系数（k） /
- 分析算法 /
- 资源评价 /
- 天然气
Abstract:Objective Sequential reservoir size analysis based on the Pareto principle encounters challenges in accurately determining the coefficient '
k ', which quantifies the gradient of resource scale variation, thereby limiting the approach's effectiveness.Methods This study proposes an optimized methodology for calculating '
k ' by analyzing the scale ratio of discovered resources and employing possible sequential numbers. This approach involves establishing a cross-plot with sequential numbers andk -axis values based on calculated ratios, locating combinations of data points from various ratios that form approximately straight vertical lines against thek -axis, and identifying the intersection points on thek -axis as solutions fork . Further optimization principles are suggested to enhance result selection to meet resource assessment requirements.Results Reanalysis of classic datasets from academic literature validated the methodology's capability in accurately determining the coefficient (
k ). A case study of tight gas reservoirs, specifically the 6th group of Jurassic Shaximiao formations in the Yanting Block of the Jinqiu gas-producing area in the central Sichuan Basin, demonstrated favorable linear fitting results between forecasted and actual data. The calculated resource scale is in strong alignment with established tight gas exploration outcomes in the Sichuan Basin.Conclusion The proposed methodology reduces reliance on geological experience, eliminates the need for complex determinant models or matrix manipulations, and minimizes subjectivity and computational complexity in parameter selection. Additionally, the algorithm is available as a coded computer program, enhancing its practical efficiency and applicability in sequential reservoir size methods.
-
油气资源评价的技术思路是基于科学原理，可分为成因法、类比法和统计法3类，其中成因法根据生烃量计算结果，求取烃类物质的资源聚集量；类比法根据不同地区在油气地质条件上的相似性量化结果，利用类比思路获取评价结果；统计法则是利用历史经验的趋势推断法，即利用历史勘探成果资料，通过数学统计分析，对资源潜力构建预测模型，实现对资源规模的定量表征[1-2]。3类评价思路各有优点与不足，其中：
（1）成因法根据油气有机地球化学原理，对烃类物质生成总量获取计算结果，在定量表征烃类物质供给上具有明显的优点，但不足之处在于对与油气资源运聚相关的关键参数取值难度较大，且由于生烃量计算结果在数值上通常较高，因此应用该类技术思路所获取资源量的乐观程度也一般较高。
（2）类比法的优势在于选用参数较多，与油气地质条件联系紧密，适用于不同勘探阶段，但对基础地质资料的分析精度和掌握程度的要求高；且地质参数分级标准的建立对勘探经验依赖较大，该类技术思路的评价结果一般较乐观。
（3）统计法的优势在于与勘探成果和油气发现的相关性好，可量化表征勘探趋势，对具有一定勘探程度的区块及区带级的资源评价有优势，但也受勘探成果资料的制约，在应用中对未来经济发展及勘探技术改进的体现程度较低，该类技术思路的评价结果通常趋稳健。
规模序列法是统计法评价技术中的一种[3]。该方法在技术思路上认为如将评价目标中已发现和待发现的全部油气藏按规模由大至小进行排序后，其形成的序列服从Pareto定律[4-6]。因此利用该定律，可获取评价目标的资源规模[7-8]。该方法的特点是依靠已发现的油气藏规模，利用统计模型，获取评价目标资源规模 [9-10]。规模序列法所具有的优势包括预测模型（Pareto分布模型）的表达简捷清晰、方法原理直观易懂、与已发现油气藏联系紧密等，在对四川、渤海湾、准噶尔、珠江口等盆地的油气资源评价中，不同学者应用该方法均获取了资源评价结果，进一步揭示了其适用性[11-15]。但在规模序列法的应用中，也存在对关键参数的确定难度大、主观性强、相关分析过程复杂繁琐等问题，带来了规模序列法资源评价分析结果在数值上的不确定性，制约了规模序列法在资源评价工作中的成效。
1. 问题的提出
规模序列法的理论基础是Pareto定律。其中，油气藏规模变化系数（k）的取值对规模序列法的应用非常重要，直接关系到评价结果的获取[16-17]。但k值的确定，一直以来是规模序列法应用中的难点之一[18-19]。目前存在的技术问题主要包括：
（1）对k直接赋值的地质勘探经验依赖程度高，主观性强：当k是基于地质经验的直接主观赋值，而不是通过定量计算所获取时，其取值依据往往难以说明。
（2）通过复杂的行列式-矩阵运算，仅以标准差作为对比标准，实际不足以确定k的取值。
以《石油数学地质概论》[20]中所列经典数据为例，已发现油气资源规模由大至小分别为149.143万，61.567万，34.375万，27.277万t，对k取值的分析结果为
1.7321 ，认为当对应油气规模序列号分别是3，5，7，8时，使预测值和实际值之间的标准差达到最小（0.00094 ），因此是“正确的”序列。但分析结果表明，至少可以存在另一组k的取值（
0.2161 ）和油气田序列（2，120，1780 ，5191 ），可使预测值和实际值之间的标准差（0.00036 ）小于文献[20]中所给出的最小标准差（0.00094 ）。（3）既有技术相关运算较复杂，矩阵运算技术步骤多达11步，且迭代分析中需要设定步长，而步长之间的部分则被略过了，可能加剧了分析误差。
基于Pareto定律的常用表达式，通过获取资源规模比后，明确规模序列号与油气藏规模变化系数（k）间的相关性，构建了一种改进的对油气藏规模变化系数（k）的取值技术，可应用于规模序列法资源评价中，有效解决了上述问题。
2. 对油气藏规模变化系数（k）的取值技术构建
2.1 技术步骤
（1）规模序列法评价中对Pareto定律常用的表达式为[20]：
(QmQn)=(nm)k， (1) 式中：Qm为序列号为m的油气藏规模；Qn为序列号为n的油气藏规模；m，n为评价单元内任意2个油气藏，在已发现和待发现的全部油气藏内，根据规模由大至小排序后，它们所处的位置序列号；k为油气藏规模变化系数。
对式（1）可进一步表达为以下形式：
logycAij=k， (2) 式中：c为对某一组已发现的i个（i3），且按规模由大至小排序后的油气资源数据，其中相对规模最大的油气藏所对应的潜在规模序列号；y为某一潜在的油气规模序列号（y为正整数，且y>c）；Aij为在该组已发现油气资源规模数据中，某个非相对规模最大的油气藏（j）与相对规模最大的油气藏（i）间的规模比。
（2）将已发现油气资源按规模由高至低排序，依次计算对应的Aij（规模比）。
（3）将已发现最大油气藏所可能具有的规模序列号（c），作为控制性可变条件，从c=1开始，依次对不同c取值条件下，计算$ y/c$，其中y为自然数，从c+1开始，且单调递增，相邻两者之间间隔为1，一般而言，c在取值上通常不超过20，y在取值上通常不超过
1000 。（4）获取在此条件下$ \mathrm{log}_{\frac{y}{c}}A_{ij} $的系列计算结果，作为k的潜在取值的表征。
（5）以y为纵轴，分别以不同规模比Aij取值条件下的$ \mathrm{log}_{\frac{y}{c}}A_{ij} $计算结果为横轴，构建交会图。
（6）根据交会图上的数据点分布，按图上数据点由低至高，在参数取值上y和规模比Aij由小至大的方式，寻找与y轴平行或近平行的交会数据点组合，其拟合线与横轴的交点，即为在对某c取值条件下，所获取的一个k的解（即沿着横轴的数值减小方向，观察不同规模比下的数据点，寻找其中位于一条垂线，或者近似位于一条垂线上的数据点组合）。
（7）重复步骤（3）～（6），直至在c的其他取值条件下的相关计算和分析完成，形成在一定c取值范围内对k的解集。
2.2 理论算例
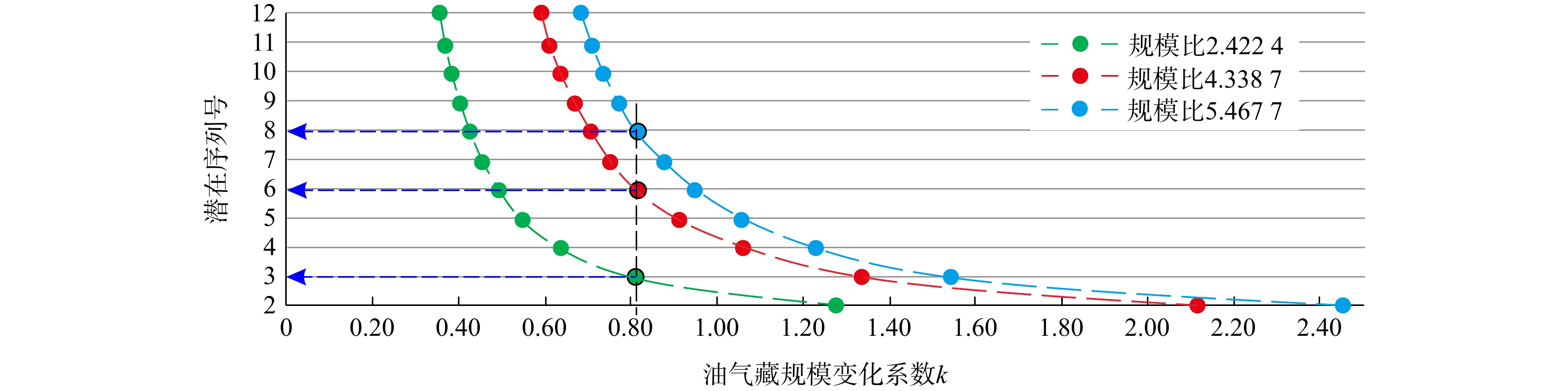
仍以《石油数学地质概论》[20]中的数据集合为例，其表征规模比的数组为：$\left[\dfrac{149.13}{61.567}\approx2.422\ 4， \dfrac{149.13}{34.375}\approx4.338\ 7，\dfrac{149.13}{27.277}\approx5.467\ 7 \right] $。
当c=1，即假设规模为149.13万t的油藏的潜在序列号为1时，根据式（2）则有：
logyb12.422 4=kb， (3) logyc14.338 7=kc， (4) logyd15.467 7=kd， (5) 式中：yb，yc，yd分别为规模为61.567万，34.375万，27.277万t的油藏的潜在序列号（yb，yc，yd均为正整数，且1<yb<yc<yd）；kb，kc，kd均为油气藏规模变化系数。
由此可分别构建在c=1时，不同取值条件下yb，yc，yd对k的映射关系表及交会图，例如，当yb=2，则kb=${\mathrm{log}}_{\frac{2}{1}}2.422\ 4 $=
1.2765 ；当yc=3，则kc=${\mathrm{log}}_{\frac{3}{1}}4.338\ 7 $=1.3358 ，其余以此类推（表1）。表 1 针对某算例c=1条件下潜在序列号对油气藏规模变化系数（k）的映射关系Table 1. Correlations of the potential number with the sequence and the coefficient of the resource scale variation (k) under the condition of c=1 for a certain study case潜在的油气资源规模序列号
（yb，yc，yd）油气藏规模变化系数k kb kc kd 2 1.2765 2.1173 2.4509 3 0.8054 1.3358 1.5464 4 0.6382 1.0586 1.2255 5 0.5497 0.9119 1.0556 6 0.4938 0.8191 0.9482 7 0.4547 0.7542 0.8730 8 0.4255 0.7058 0.8170 9 0.4027 0.6679 0.7732 ··· ··· ··· ··· 注：c为发现最大油气藏所对应的潜在规模序列号；yb，yc，yd分别是规模为61.567万，34.375万，27.277万t的油藏的潜在序列号，yb，yc，yd均为正整数，且1<yb<yc<yd；kb，kc，kd均为油气藏规模变化系数；下同 对比表2中获取的kb、kc和kd，可以看出当以0.02作为精度条件时，对潜在序列号为3，6和8而言，其计算值分别为
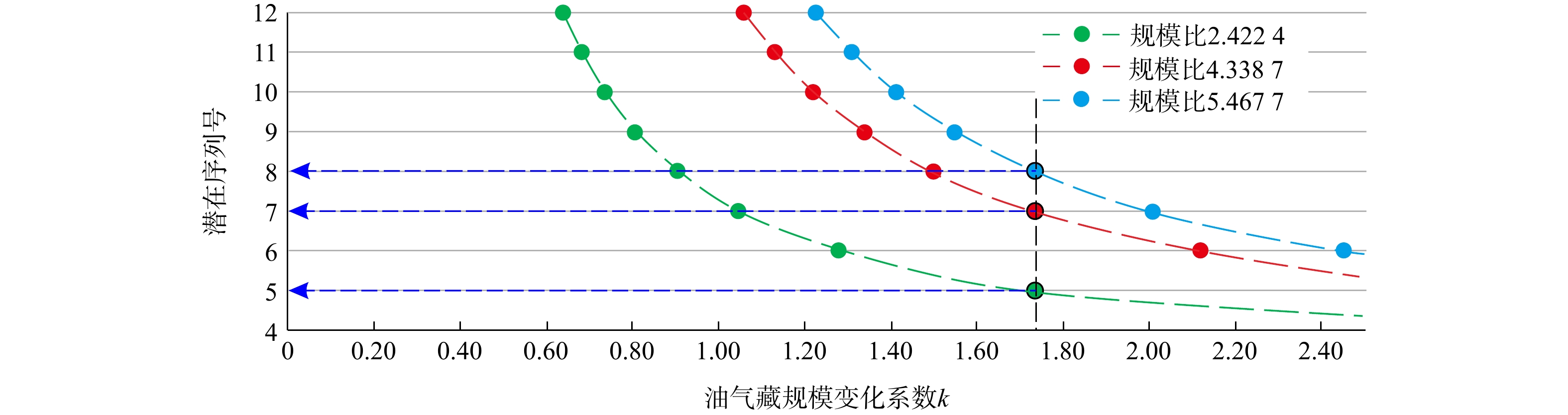
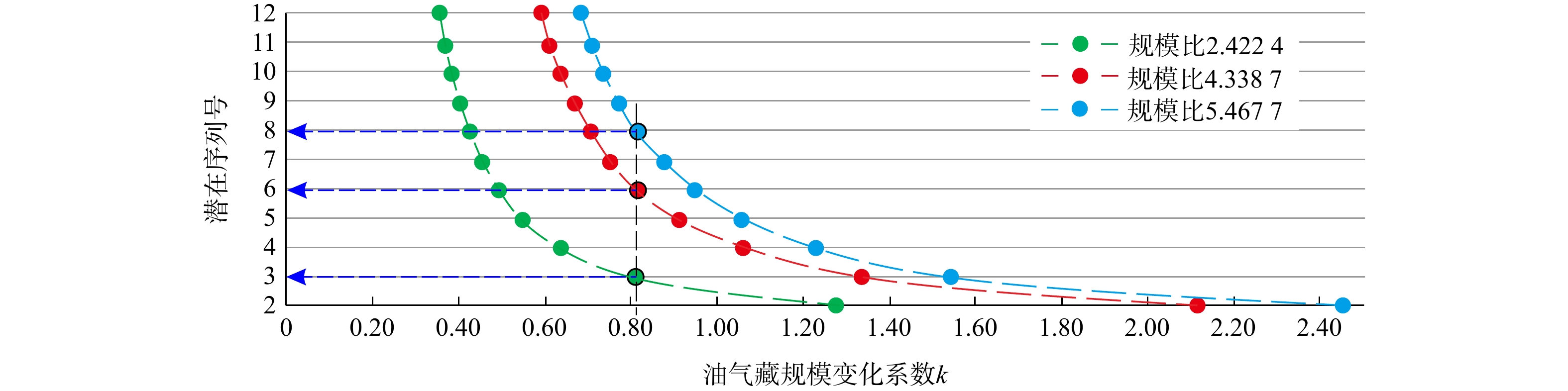
0.8054 ，0.8191 和0.8170 ，以此计算|kb-kc|、|kd-kc|和|kb-kd|，其结果均小于0.02，又由于c=1，表明资源规模序列号（1，3，6，8）为一组该精度条件下的有效解，对应k的取值为$ \dfrac{k_{\mathrm{b}}+k_{\mathrm{c}}+k_{\mathrm{d}}}{3}\approx 0.814\ 0 $，在图1上表现为对应数据点均近似位于一条与x轴垂直的直线上。表 2 针对某算例c=3条件下潜在序列号对油气藏规模变化系数（k）的映射关系Table 2. Correlations of the potential number with the sequence and the coefficient of the resource scale variation (k) under the condition of c=3 for a certain study case潜在的油气资源规模序列号
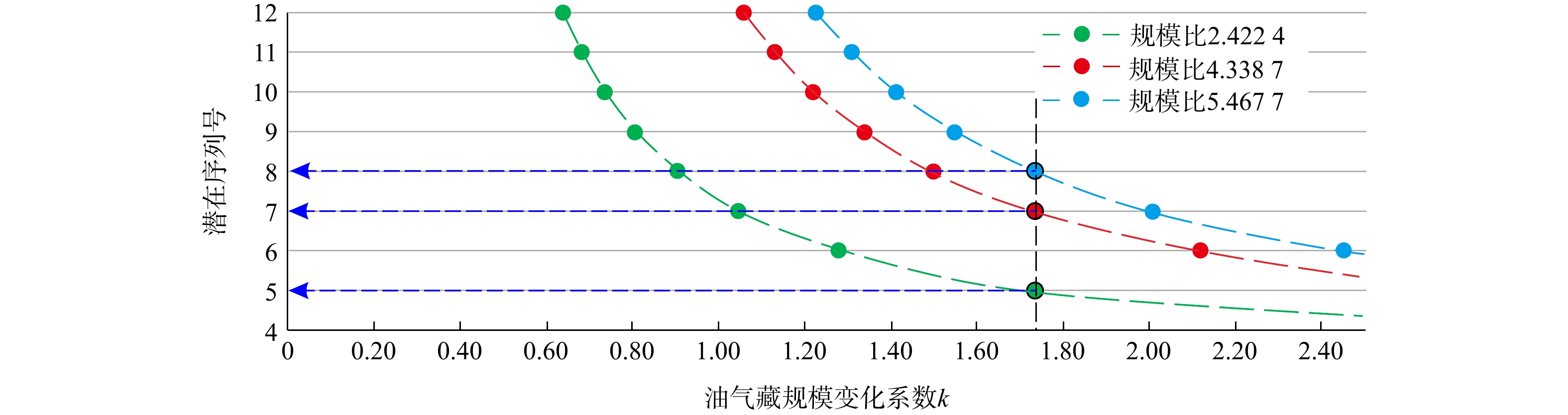
（yb，yc，yd）油气藏规模变化系数k kb kc kd 4 3.0755 5.1014 5.9053 5 1.7321 2.8729 3.3257 6 1.2765 2.1173 2.4509 7 1.0442 1.7321 2.0050 8 0.9021 1.4963 1.7321 9 0.8054 1.3358 1.5464 ··· ··· ··· ··· 
图 1 潜在序列号与油气藏规模变化系数（k）交会图（c=1时）Figure 1. Cross-plot between the potential number with the sequence and the coefficient of the resource scale variation (k) under the condition of c=1以此类推，可知对于c=2、c=3及c等于其他正整数时，也可按照上述过程对k及油气资源规模序列号进行分析求解，其中当c=3时，所获解即为文献[20]中给出的“正确解”：油气资源规模序列号为3，5，7，8时，k的取值对应约为
1.7321 （表2，图2）。
图 2 潜在序列号与油气藏规模变化系数（k）交会图（c=3时）Figure 2. Cross-plot between the potential number with the sequence and k under the condition of c=3因此基于不同已发现最大规模油气藏的潜在规模序列号c取值条件，通过构建潜在序列号与k取值间的映射关系，可实现对k及已发现油气藏规模序列号组合的图解取值（图1，2）。
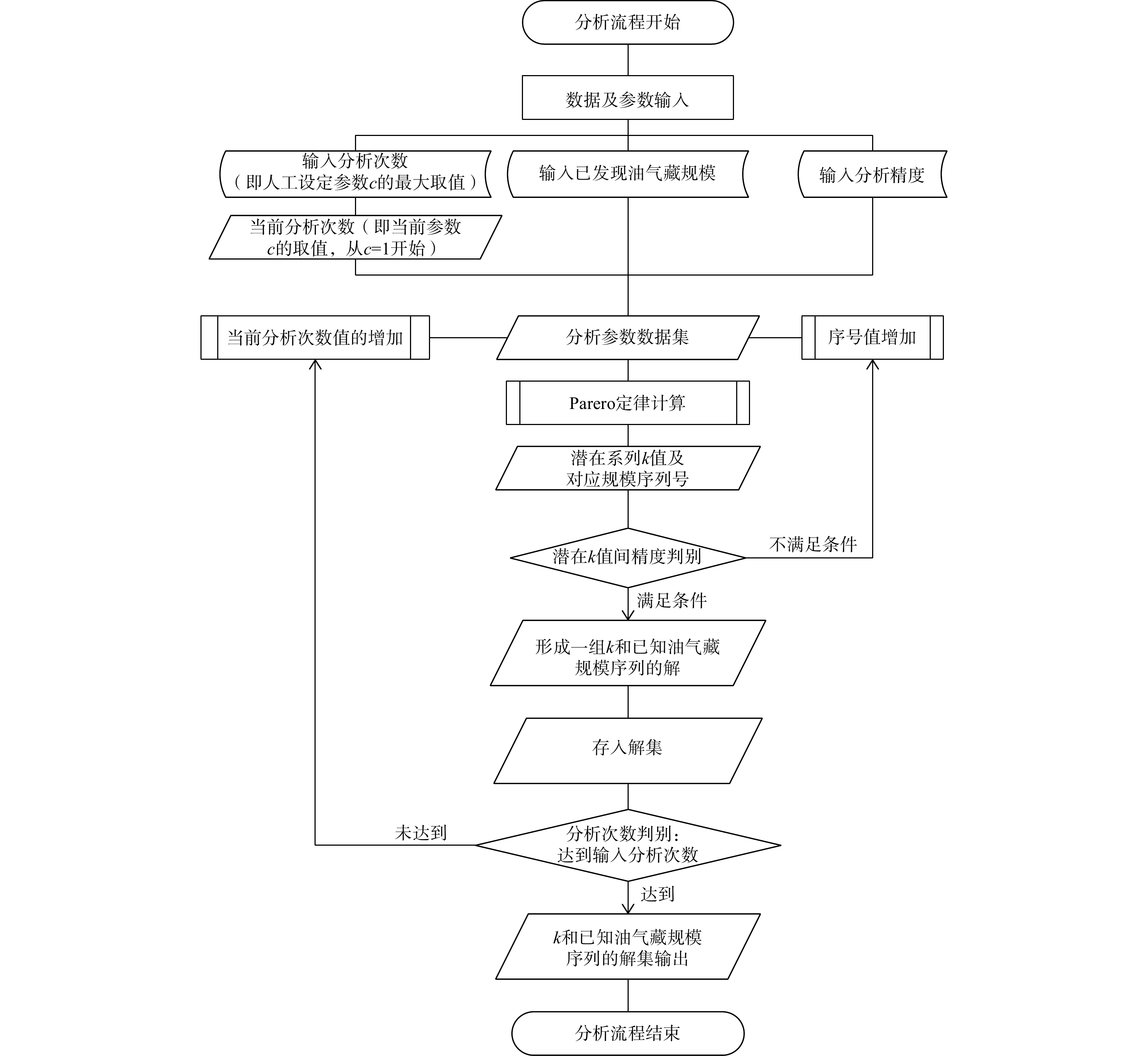
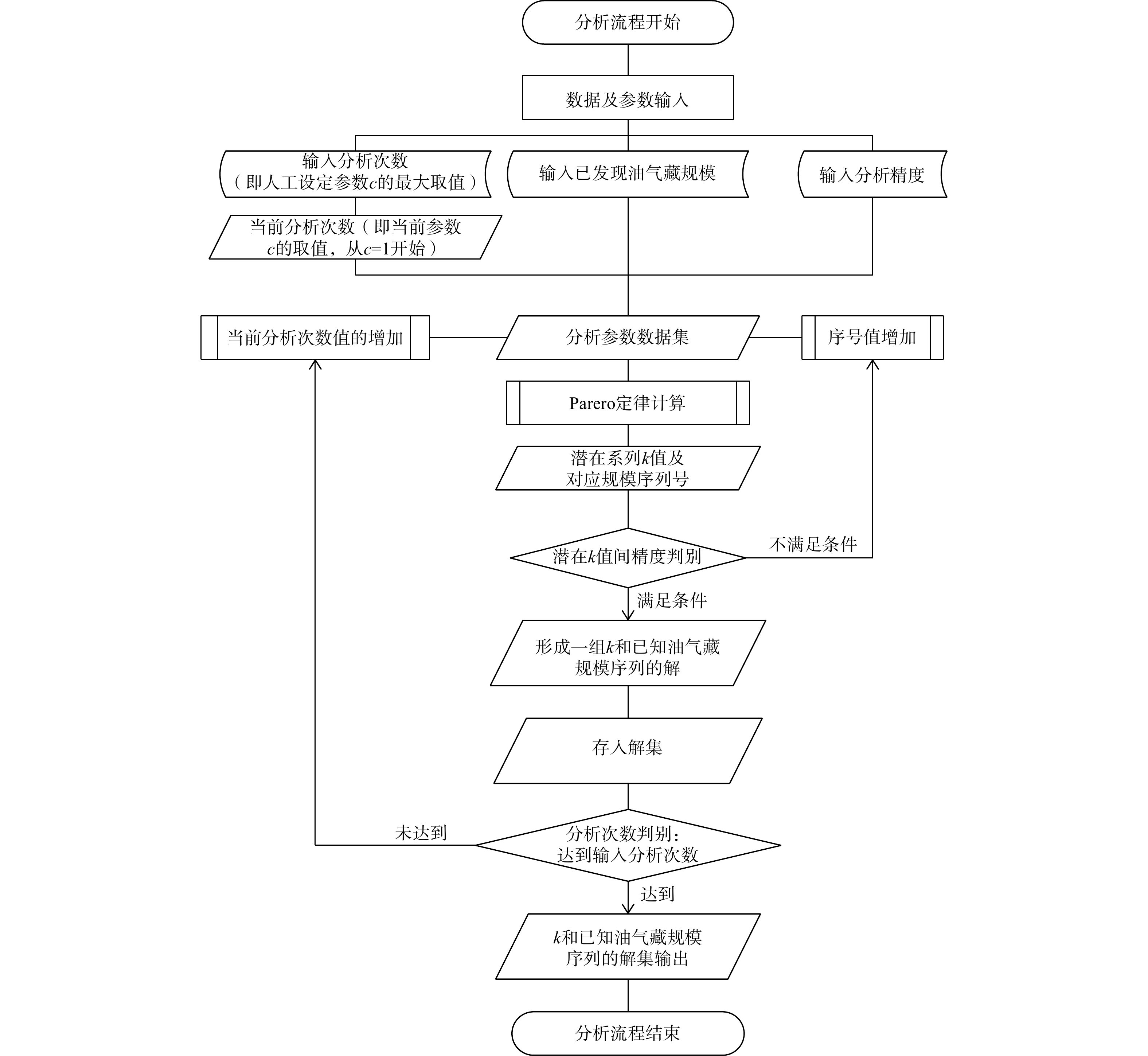
对上述技术过程，目前已基于Python 3.0，实现了程序化，可快速自动获取油气藏资源规模变化系数k和其所属规模序列，程序设计流程如图3所示。
图 3 对规模序列法中油气藏资源规模变化系数（k）及已知油气藏序列号分析的Python程序流程设计图Figure 3. Design of the Python workflow for analyzing k and the sequential number for the reservoir size sequential method2.3 对k取值和油气资源规模序列的确定原则
根据式（1）可知，当规模序列号增加时，通过该式计算获取的资源量值始终为正，因此需要设定“最小经济油气藏规模”以“截断”序列[21-23]。又由于在不同k的取值和已发现油气资源规模序列号的组合条件下，资源评价结果会存在很大差异[23]。因此为有效获取资源规模评价结果，需对k和油气规模序列解集确定取值原则，包括：
（1）已发现最大油气资源规模的序列号（即c的取值）不宜过大。
（2）已发现最大油气资源规模的序列号与次大的油气资源的规模序列号间的间隔不宜过大。
（3）“最小经济油气藏规模”在油气资源规模序列中所对应的序列号，不宜过大。
（4）对k取值分析精度的选取应适宜，不宜过高。
对原则（1）和（2）设定的原因：当最大已知油气藏的序列号过大，或规模次大的油气藏所具有的序列号与c的差值相对过大时，则在对待发现油气藏规模预测中，按规模序列法的应用原理，进行计算并累加求和，结果会明显过于乐观，直至与当前勘探经验不符乃至矛盾。
对原则（3）和（4）设定的原因：最小经济油气藏规模所对应的序列号如果很大，则说明油气资源规模序列中包含的有效油气藏数量很多；另一方面，分析精度过高会使获取的油气资源规模序列总体偏长，造成预测出的待发现油气藏数量过多；由于在分析过程中，已发现油气藏数量是确定的，因此当待发现油气藏过多时，会造成评价结果过于乐观，并在对资源量的累加求和中，形成与勘探经验性认识的矛盾。
在对不同算例[14，20，23]进行反复测算的基础上，目前认为分析精度取0.01～0.02，即可满足规模序列法分析中对结果合理性和数值准确性的兼顾需求。
3. 与既有方法对比
所提出的对油气藏规模变化系数（k）的取值技术，基于已发现油气藏规模所具有的数据结构特征，与目前既有的其他相关技术对比，主要包括以下4方面技术特点：
（1）不需要设定k的初始值，避免了因初始取值选择不恰当造成的分析结果不合理。
（2）对迭代步长无需进行设定，实现了对k取值的连续分析，有助于分析精度的提升。
（3）不用建立矩阵并对其进行求秩计算，降低了分析过程中相关计算的复杂程度。
（4）通过对已发现油气藏规模的定量计算，实现对油气藏规模变化系数（k）解集的获取，降低了对勘探主观经验的依赖程度（表3）。
表 3 不同技术特点对比Table 3. Contrast in traits among different means特点 本次研究提出的方法 矩阵计算 直接赋值 结果客观性 基于已发现资源规模数据；计算相对客观 对地质经验依赖程度高；相对更主观 计算复杂程度 不需要进行矩阵计算，可利用常用办公软件实现图解 需要进行多次矩阵计算 利用经验直接确定 计算复杂程度低 计算复杂程度高 计算复杂程度低 分析步长设置 不需要人工设定 需要人工设定 不需要人工设定 精细程度 不需要迭代，无分析步长，精细程度高 需要迭代，分析步长之间的部分被略过 经验判定，精细化程度低 分析结果形式 对不同条件下对k取值的解集，相对更完整，利于评价与优选 解集中的单个解 4. 应用实例
在研究中，除对上述已发表文献中的相关算例数据进行分析外，还针对四川盆地金秋气区盐亭区块侏罗系沙溪庙组6号砂组的天然气资源构建了应用实例。
4.1 已发现资源规模
四川盆地是我国以天然气为主的重要含油气盆地，陆相地层是盆地天然气资源重要的赋存层系[24-25]。除传统的三叠系须家河组外，川中侏罗系沙溪庙组目前已成为盆地陆相天然气勘探热点，金秋气区盐亭区块是“川中核心建产区”的重要组成部分；在近年取得突破后，该气区沙溪庙组的天然气资源潜力有待进一步评价[26-27]。
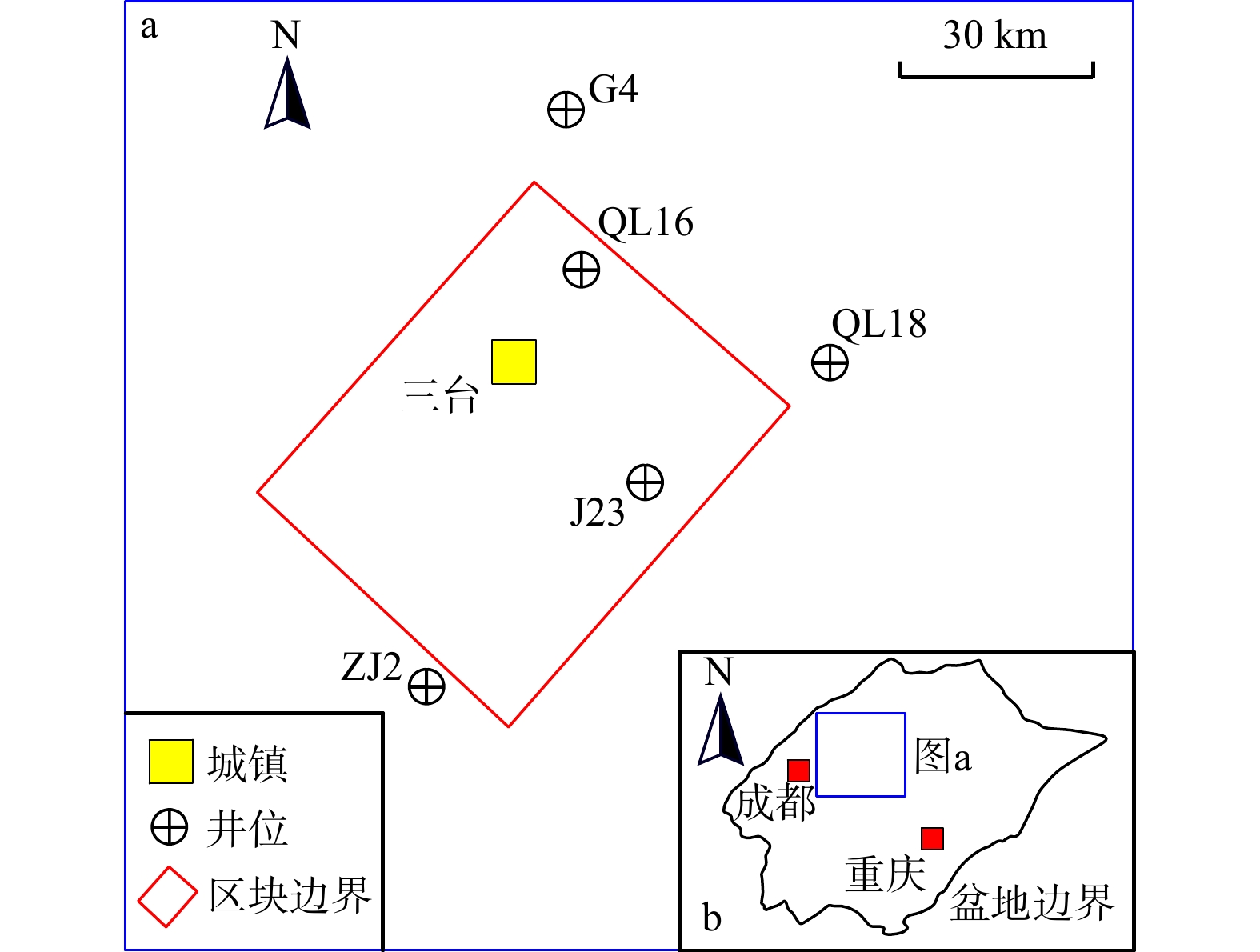
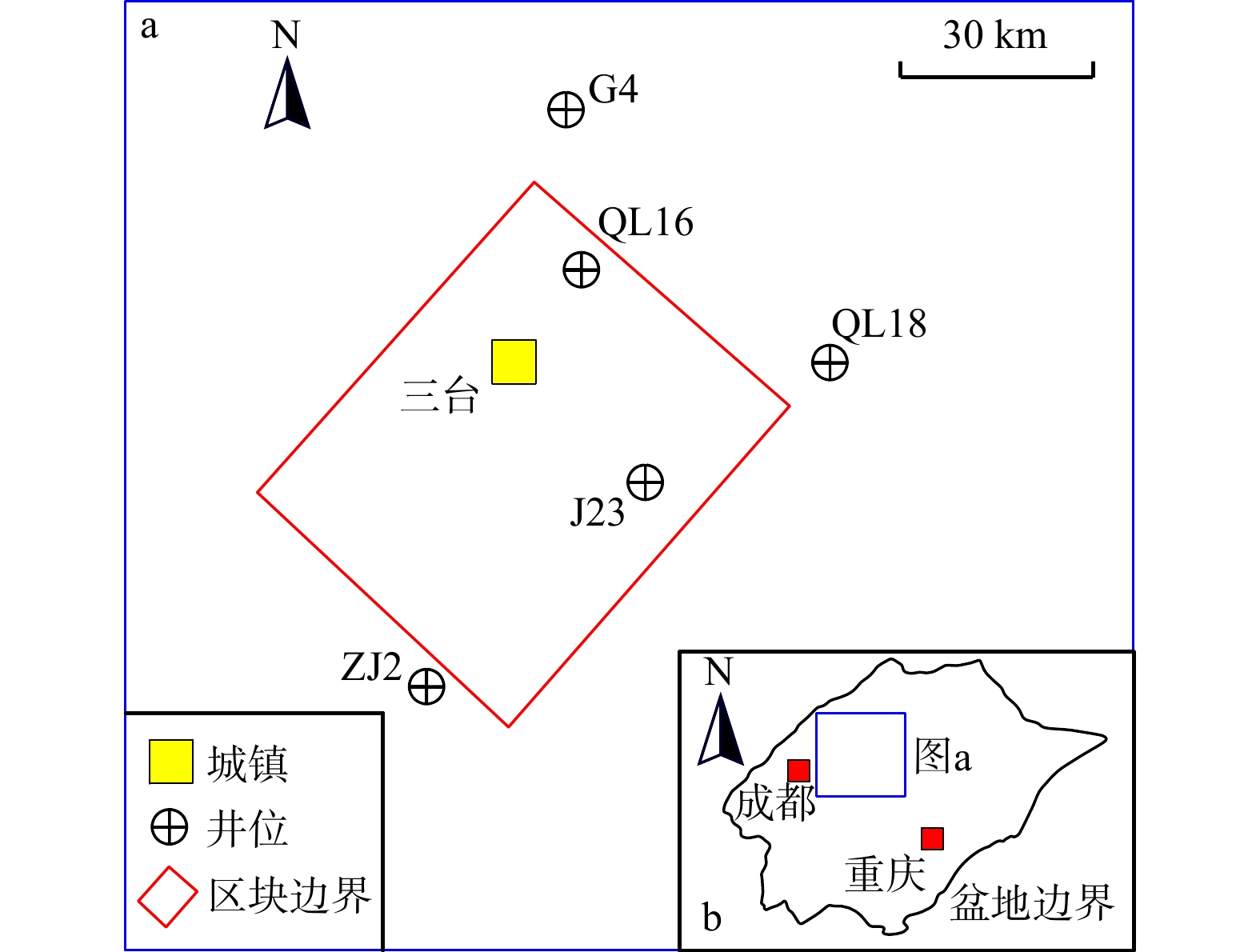
在该应用实例中，已发现气藏来自于同一砂组，从油气地质学的角度看，具有成因上的联系，但由于资源聚集部位在空间分布上存在差异，又在一定程度上存在彼此间作为气藏的独立性。此外在金秋气区，针对该砂组目前已实施了多口探井和开发井，具有一定的勘探程度，因此可以利用油气资源规模序列法对其开展评价。区块位置和已发现资源规模数据见图4和表4。
图 4 川中金秋气区盐亭区块（应用实例）盆地位置示意图Figure 4. Location of the Yanting Block (application case) of the Jinqiu gas-producing area located in the central part of Sichuan Basin表 4 川中金秋气区盐亭区块侏罗系沙溪庙组6号砂组已发现资源规模Table 4. Scale of discovered reservoirs in the 6th group of Jurrasic Shaximiao Formation in the Yanting Block of the Jinqiu gas-producing area located in the central part of Sichuan Basin已发现气藏名称 JQ23 JQ517 JQ518 JQ507 JH51-ST1 ZQ2 天然气资源规模/
108m396.88 0.78 6.87 3.67 6.86 35.07 4.2 三项约束性参数设定
根据所提出方法的分析步骤，需设定分析次数、分析精度及最小经济气藏规模3项约束性参数的取值：
调整 “分析次数”，会使解集中所含k及规模序列解的数量发生变化。
调整“对k取值的分析精度”，精度越高，则会使已发现气藏的规模序列号最大值和最小值之间的范围变大，反之则会变小。
调整 “最小经济气藏规模”时，当该参数取值变小时，会使有效的规模序列号的数量增多，从而使待发现气藏的预测结果增多，反之则会减小。
按所提出的确定原则，对分析次数的设定为20，表明作为当前已发现的最大规模气藏，其可能具有的最小的规模序列号为20；对k取值的分析精度取值为0.01；对最小经济气藏规模的取值，基于当前的勘探经验及气藏开发实际，基于经验值取值为0.5×108 m3。
4.3 通过分析获取解集
根据前述所提出方法，可获取k的取值、已发现气藏的序列号组合，及最小经济气藏规模所对应的序列号（表5）。
表 5 应用实例k、已知气藏规模序列号、最小经济气藏规模对应序列号求解结果Table 5. Results acquired from the calculation analysis of the cofficient of the resource scale variation (k), sequential number of discovered reservoirs and sequential number corresponding to the minimum economic gas reservoir size for the application case分析次数（即参数c的取值） 求解结果 已知气藏的规模序列号 气藏规模变化系数k 最小经济气藏规模条件下所对应规模序列号 1 [1, 3, 17, 17, 32, 174] 0.9345 280 2 [2, 5, 21, 21, 37, 149] 1.1201 220 3 [3, 6, 18, 18, 28, 79] 1.4721 107 4 [4, 8, 24, 24, 37, 105] 1.4735 142 5 [5, 9, 23, 23, 33, 81] 1.7328 104 … … … … 20 [20, 31, 63, 63, 83, 161] 2.3129 194 研究中进一步根据应用实例，利用基于行列式-矩阵的迭代算法对关键参数进行了分析求取，并与所提出方法进行了结果对比。采用相关计算软件-常规与非常规油气资源评价软件（HyRAS 2.0）的分析模块，得到对已知气藏规模序列号组合的分析结果为[5, 9, 23, 23, 33, 81]（即表5中分析次数等于5（c=5）时，已发现气藏所对应的规模序列号），获取在此规模列序列号组合条件下，对k的取值约为
1.7321 （即tan（60°））；该结果与表5中在相同规模序列号组合条件下的气藏规模变化系数（k）（1.7328 ）非常相近，说明2种方法在结果上的可印证性；另一方面，此应用实例中利用提出方法所获结果的标准差相对更小，表明与实际相比，其在数值上的偏差更低（表6）。表 6 行列式-矩阵迭代算法结果与所提出方法中相应解对比情况Table 6. Contrast between the results of determination-matrix iteration and the corresponding solution from the proposed method已发现气藏规模序列号 天然气资源规模/108m3 实际规模 行列式-矩阵迭代算法应用结果k= 1.7321 所提出方法应用相应解k= 1.7328 5 96.88 96.7400 96.8800 9 35.07 34.9500 34.9863 23 6.87 6.8800 6.8835 6.86 6.8800 6.8835 33 3.67 3.6800 3.6824 81 0.78 0.7800 0.7769 标准差 0.0759 0.0428 根据Pareto定律及最小经济气藏规模取值结果，结合上述气藏规模变化系数（k）及已发现气藏规模序列号组合作为计算条件，得到资源量计算结果分别为
3061.80 ×108 m3（行列式-矩阵迭代算法）和3085.30 ×108 m3（所提出方法）。由于当前在6号砂组内已发现天然气资源规模总计为150.13×108 m3，并已具有一定的勘探程度，分析认为该结果可能相对过于乐观，说明除进行标准差计算外，为满足资源量获取结果的合理性，还应在获取上述解集后，进一步对解集进行优选，以确定关键参数和已发现气藏序列号组合的取值。4.4 对解集的优选及评价结果
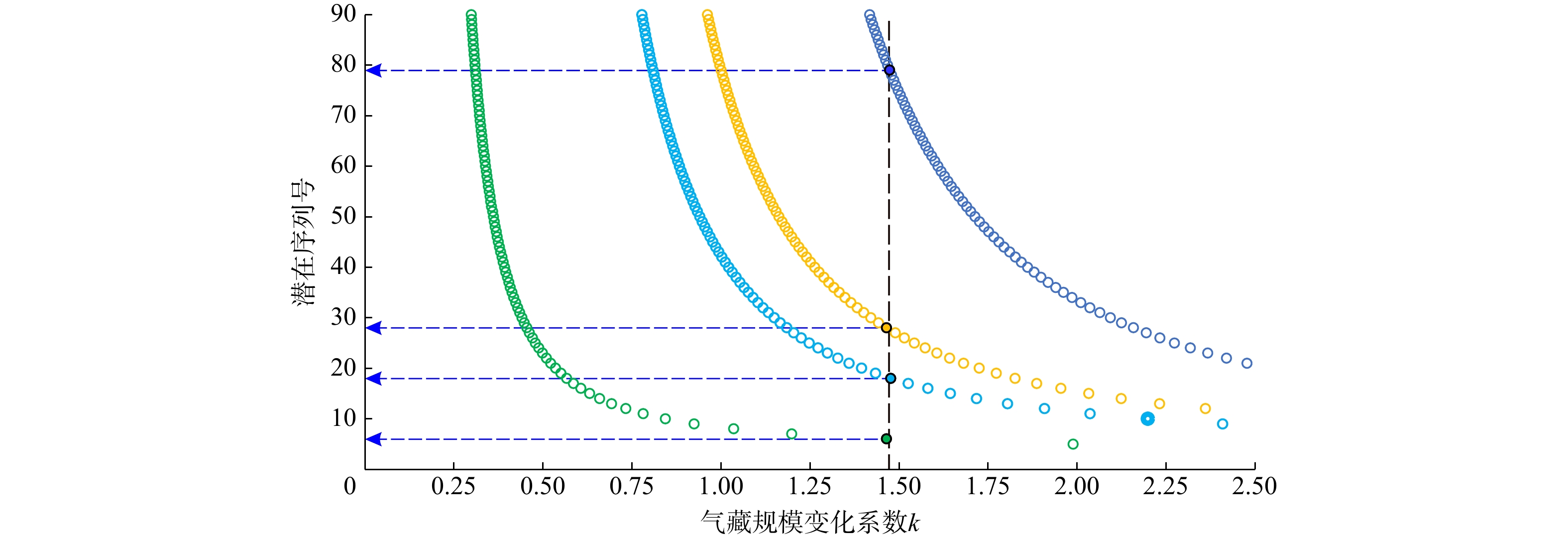
根据表5可知，当c=3时，对应解中气藏规模变化系数（k）的取值为k=
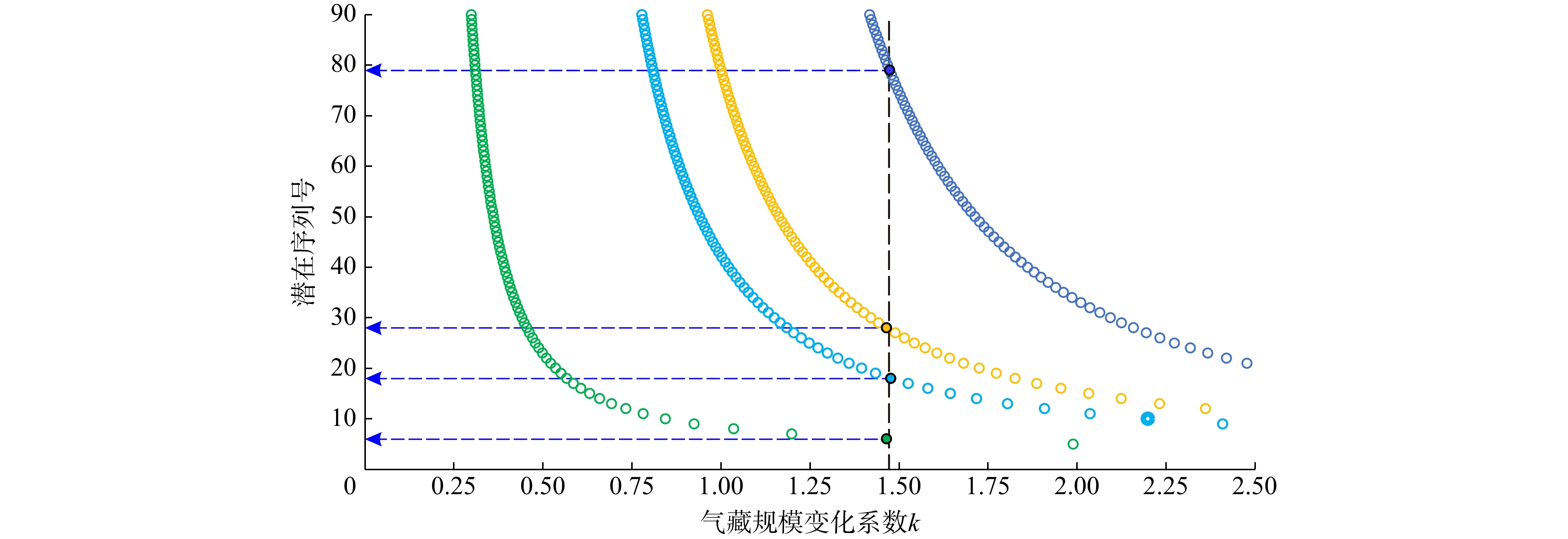
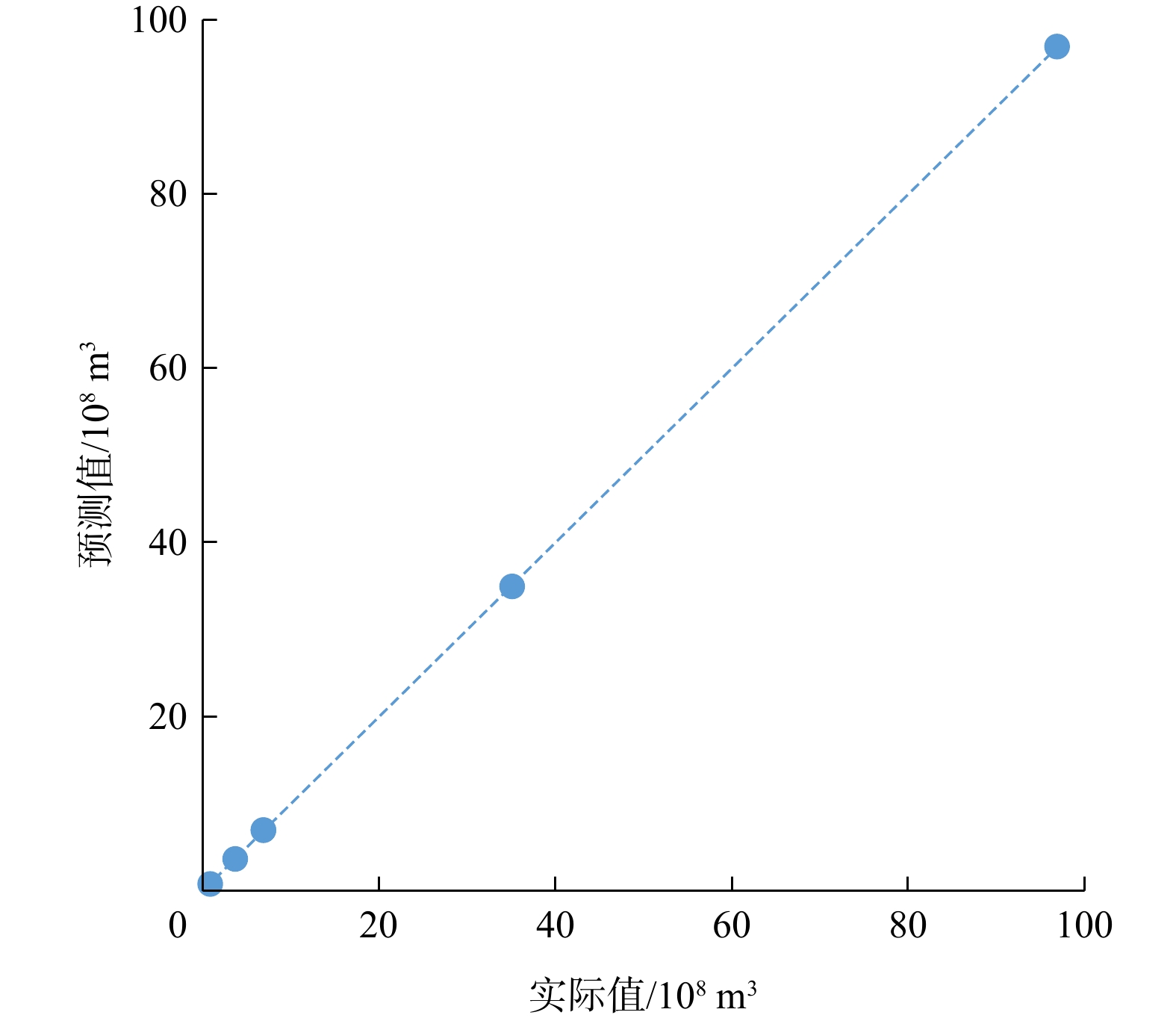
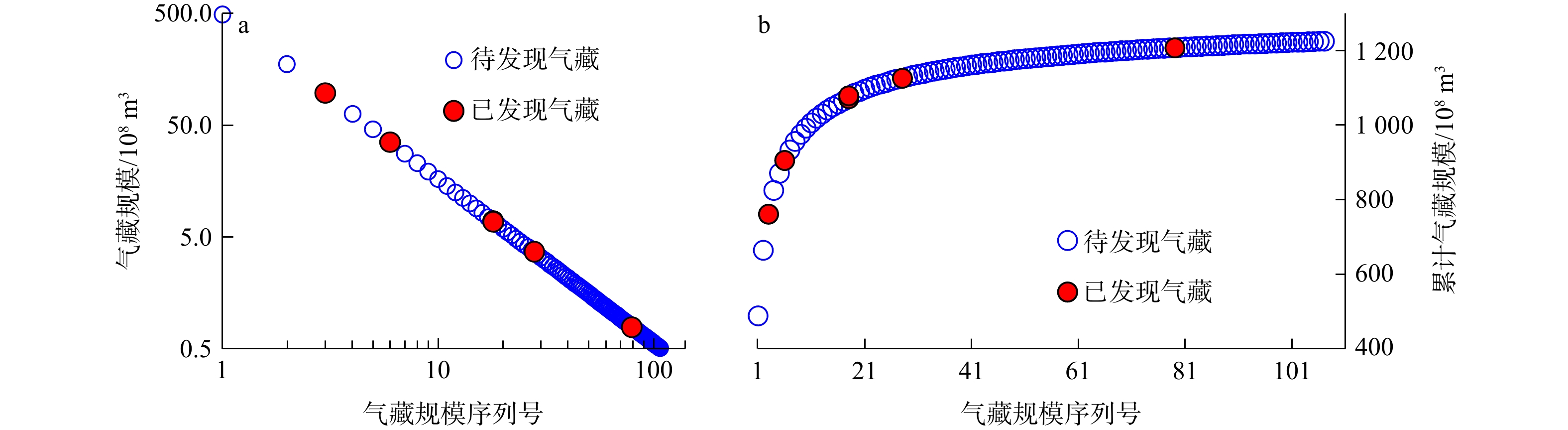
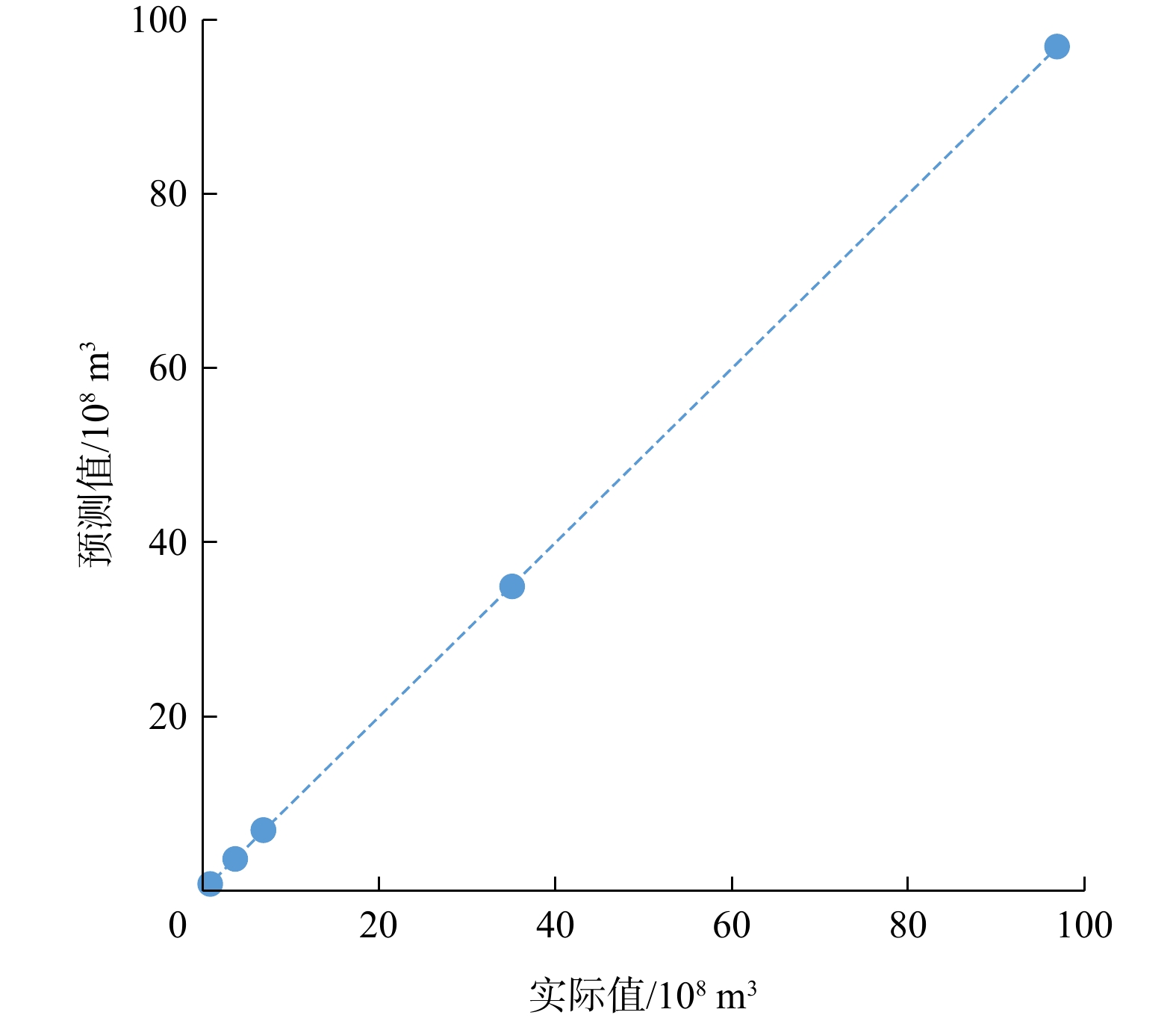
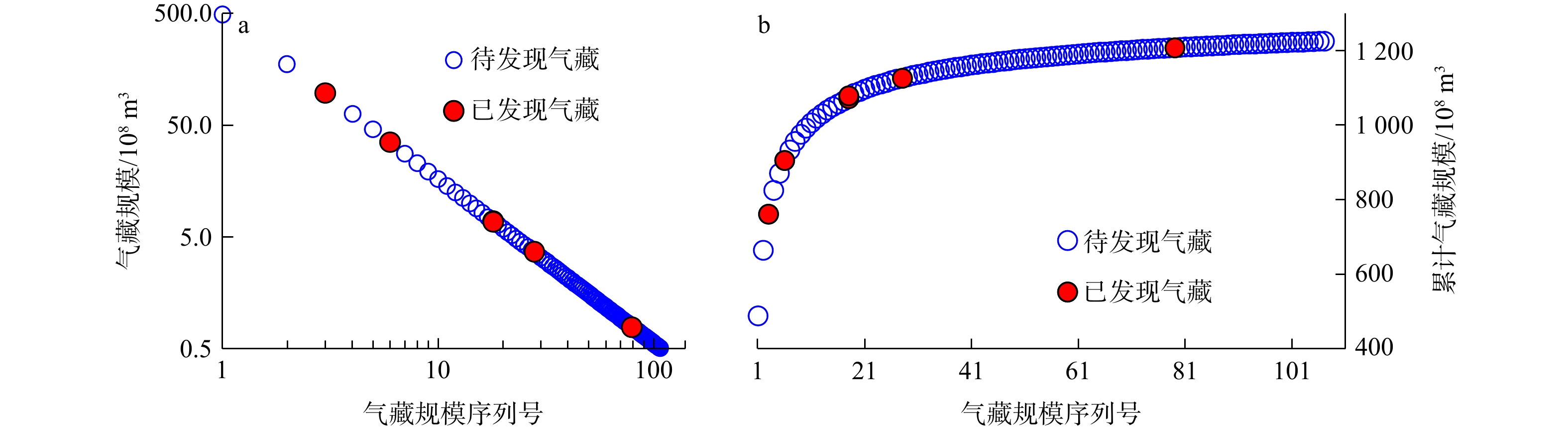
1.4721 ，已知气藏所具有的规模序列号组合为[3, 6, 18, 18, 28, 79]，其中：已知最大规模气藏具有的序列号为3，相对比较靠前；最大和次大已知气藏间的规模序列号差相对较小，表明分析结果相对谨慎，未偏向过于乐观，说明在当前已发现最大规模气藏的基础上，该区仍有一定勘探潜力（序列号1及2均对应为待发现气藏，其根据Pareto定律获取的资源潜力分别为488.2074 ×108 m3和175.9779 ×108 m3），体现了天然气资源评价中一定的预测性和稳健的勘探预期（即未来还可能进一步获取较大的勘探发现）；满足最小气藏规模标准（≥0.5×108 m3）下的最大规模序列号取值为107，在所获的该参数取值中相对较低；与所获解集中的其他解相比，该解相对更为适宜（图5）。
图 5 应用实例潜在序列号与气藏规模变化系数（k）交会图（c=3时）Figure 5. Cross-plot between the potential number with the sequence and k under the condition of c=3 (application case)在确定解集中的一组解后，即可根据该组解中已发现气藏的规模序列号和气藏规模变化系数（k）的取值及最小经济气藏规模，构建完整的资源规模序列；进行计算后可获取对已知气藏规模的预测值，其与实际值的交会拟合结果表明，两者之间差异很小（图6）。
图 6 已知气藏规模预测值和实际值交会图Figure 6. Cross-plot between forecast and actual values at the scale of gas resources在此基础上，对通过相关分析获取的已发现和待发现气藏规模进行累加求和，得到基于Pareto定律该实例的资源规模序列法评价结果，为
1225.51 ×108 m3；经熟悉该气区的气田勘探科技工作者的讨论，认为该结果比较符合实际情况及未来勘探预期（表7，图7）。表 7 应用实例的气藏序列分析结果Table 7. Results obtained from the analysis for the application case of the reservoir size sequential method气藏规模
序列号气藏规模/
108m3气藏规模
变化系数k最小经济
气藏规模/108m31 488.2074 1.4721 0.5 2 175.9779 3 96.8800 4 63.4325 5 45.6721 6 35.0700 7 27.8314 8 22.8647 9 19.2249 ··· ··· 105 0.5167 106 0.5095 107 0.5025 
图 7 应用实例天然气资源规模与规模序列号交会图a. 气藏规模与序列号交会图；b. 累计气藏规模与序列号交会图Figure 7. Acquired sequence of gas resources for the application case5. 结 论
（1）提出了根据已知油气藏规模的数据结构特征，对油气藏资源规模变化系数（k）的优化取值方法：与既有方法相比，该方法降低了对k取值过程中的主观性和复杂性，有助于提升油气资源规模序列法的应用效果。
（2）在对已发表文献中的公开数据进行分析的基础上，以川中金秋气区盐亭区块侏罗系沙溪庙组6号砂组天然气为实例开展了方法技术应用，根据当前已知天然气气藏规模，基于上述所提出的分析方法，对气藏规模变化系数（k）的取值结果为
1.4721 ，获取的天然气资源规模为1225.51 ×108 m3。相关评价结果比较符合实际情况及未来勘探预期，对已知气藏的规模预测值与实际值的交会拟合结果较好，进一步揭示了所提出方法的有效性。所有作者声明不存在利益冲突。
The authors declare that no competing interests exist.
-
图 1 潜在序列号与油气藏规模变化系数（k）交会图（c=1时）
Figure 1. Cross-plot between the potential number with the sequence and the coefficient of the resource scale variation (k) under the condition of c=1
图 2 潜在序列号与油气藏规模变化系数（k）交会图（c=3时）
Figure 2. Cross-plot between the potential number with the sequence and k under the condition of c=3
图 3 对规模序列法中油气藏资源规模变化系数（k）及已知油气藏序列号分析的Python程序流程设计图
Figure 3. Design of the Python workflow for analyzing k and the sequential number for the reservoir size sequential method
图 4 川中金秋气区盐亭区块（应用实例）盆地位置示意图
Figure 4. Location of the Yanting Block (application case) of the Jinqiu gas-producing area located in the central part of Sichuan Basin
图 5 应用实例潜在序列号与气藏规模变化系数（k）交会图（c=3时）
Figure 5. Cross-plot between the potential number with the sequence and k under the condition of c=3 (application case)
图 6 已知气藏规模预测值和实际值交会图
Figure 6. Cross-plot between forecast and actual values at the scale of gas resources
图 7 应用实例天然气资源规模与规模序列号交会图
a. 气藏规模与序列号交会图；b. 累计气藏规模与序列号交会图
Figure 7. Acquired sequence of gas resources for the application case
表 1 针对某算例c=1条件下潜在序列号对油气藏规模变化系数（k）的映射关系
Table 1. Correlations of the potential number with the sequence and the coefficient of the resource scale variation (k) under the condition of c=1 for a certain study case
潜在的油气资源规模序列号
（yb，yc，yd）油气藏规模变化系数k kb kc kd 2 1.2765 2.1173 2.4509 3 0.8054 1.3358 1.5464 4 0.6382 1.0586 1.2255 5 0.5497 0.9119 1.0556 6 0.4938 0.8191 0.9482 7 0.4547 0.7542 0.8730 8 0.4255 0.7058 0.8170 9 0.4027 0.6679 0.7732 ··· ··· ··· ··· 注：c为发现最大油气藏所对应的潜在规模序列号；yb，yc，yd分别是规模为61.567万，34.375万，27.277万t的油藏的潜在序列号，yb，yc，yd均为正整数，且1<yb<yc<yd；kb，kc，kd均为油气藏规模变化系数；下同 
下载: 导出CSV
表 2 针对某算例c=3条件下潜在序列号对油气藏规模变化系数（k）的映射关系
Table 2. Correlations of the potential number with the sequence and the coefficient of the resource scale variation (k) under the condition of c=3 for a certain study case
潜在的油气资源规模序列号
（yb，yc，yd）油气藏规模变化系数k kb kc kd 4 3.0755 5.1014 5.9053 5 1.7321 2.8729 3.3257 6 1.2765 2.1173 2.4509 7 1.0442 1.7321 2.0050 8 0.9021 1.4963 1.7321 9 0.8054 1.3358 1.5464 ··· ··· ··· ···
下载: 导出CSV
表 3 不同技术特点对比
Table 3. Contrast in traits among different means
特点 本次研究提出的方法 矩阵计算 直接赋值 结果客观性 基于已发现资源规模数据；计算相对客观 对地质经验依赖程度高；相对更主观 计算复杂程度 不需要进行矩阵计算，可利用常用办公软件实现图解 需要进行多次矩阵计算 利用经验直接确定 计算复杂程度低 计算复杂程度高 计算复杂程度低 分析步长设置 不需要人工设定 需要人工设定 不需要人工设定 精细程度 不需要迭代，无分析步长，精细程度高 需要迭代，分析步长之间的部分被略过 经验判定，精细化程度低 分析结果形式 对不同条件下对k取值的解集，相对更完整，利于评价与优选 解集中的单个解
下载: 导出CSV
表 4 川中金秋气区盐亭区块侏罗系沙溪庙组6号砂组已发现资源规模
Table 4. Scale of discovered reservoirs in the 6th group of Jurrasic Shaximiao Formation in the Yanting Block of the Jinqiu gas-producing area located in the central part of Sichuan Basin
已发现气藏名称 JQ23 JQ517 JQ518 JQ507 JH51-ST1 ZQ2 天然气资源规模/
108m396.88 0.78 6.87 3.67 6.86 35.07
下载: 导出CSV
表 5 应用实例k、已知气藏规模序列号、最小经济气藏规模对应序列号求解结果
Table 5. Results acquired from the calculation analysis of the cofficient of the resource scale variation (k), sequential number of discovered reservoirs and sequential number corresponding to the minimum economic gas reservoir size for the application case
分析次数（即参数c的取值） 求解结果 已知气藏的规模序列号 气藏规模变化系数k 最小经济气藏规模条件下所对应规模序列号 1 [1, 3, 17, 17, 32, 174] 0.9345 280 2 [2, 5, 21, 21, 37, 149] 1.1201 220 3 [3, 6, 18, 18, 28, 79] 1.4721 107 4 [4, 8, 24, 24, 37, 105] 1.4735 142 5 [5, 9, 23, 23, 33, 81] 1.7328 104 … … … … 20 [20, 31, 63, 63, 83, 161] 2.3129 194
下载: 导出CSV
表 6 行列式-矩阵迭代算法结果与所提出方法中相应解对比情况
Table 6. Contrast between the results of determination-matrix iteration and the corresponding solution from the proposed method
已发现气藏规模序列号 天然气资源规模/108m3 实际规模 行列式-矩阵迭代算法应用结果k= 1.7321 所提出方法应用相应解k= 1.7328 5 96.88 96.7400 96.8800 9 35.07 34.9500 34.9863 23 6.87 6.8800 6.8835 6.86 6.8800 6.8835 33 3.67 3.6800 3.6824 81 0.78 0.7800 0.7769 标准差 0.0759 0.0428
下载: 导出CSV
表 7 应用实例的气藏序列分析结果
Table 7. Results obtained from the analysis for the application case of the reservoir size sequential method
气藏规模
序列号气藏规模/
108m3气藏规模
变化系数k最小经济
气藏规模/108m31 488.2074 1.4721 0.5 2 175.9779 3 96.8800 4 63.4325 5 45.6721 6 35.0700 7 27.8314 8 22.8647 9 19.2249 ··· ··· 105 0.5167 106 0.5095 107 0.5025
下载: 导出CSV
-
[1] LEE P J,WANG P C C. Prediction of oil or gas pool sizes when discovery record is available[J]. Mathematical Geology,1985,17:95-113. doi: 10.1007/BF01033149 [2] 张雪峰,罗安湘,惠潇,等. 基于层区带刻度区地质特点的资源评价方法适用性分析[J]. 地质科技情报,2016,35(4):59-65.ZHANG X F,LUO A X,HUI X,et al. Applicability of resources evaluation method on the geological characteristics of layer zone scale area[J]. Geological Science and Technology Information,2016,35(4):59-65. (in Chinese with English abstract [3] 宋振响,陆建林,周卓明,等. 常规油气资源评价方法研究进展与发展方向[J]. 中国石油勘探,2017,22(3):21-31. doi: 10.3969/j.issn.1672-7703.2017.03.003SONG Z X,LU J L,ZHOU Z M,et al. Research progress and future development of assessment methods for conventional hydrocarbon resources[J]. China Petroleum Exploration,2017,22(3):21-31. (in Chinese with English abstract doi: 10.3969/j.issn.1672-7703.2017.03.003 [4] BAKER R A,GEHMAN H M,JAMES W R,et al. Geologic field number and size assessments of oil and gas plays[J]. AAPG Bulletin,1984,68(4):426-432. [5] RAO S D. Probabilistic methods in petroleum resource assessment,with some examples using data from the Arabian region[J]. Journal of Petroleum Science and Engineering,2004,42:95-106. doi: 10.1016/j.petrol.2003.12.003 [6] CHEN Z H,SINDING-LARSEN R. Estimating number and field size distribution in frontier sedimentary basins using a Pareto model[J]. Nonrenewable Resources,1994,3:91-95. doi: 10.1007/BF02286434 [7] CHEN Z H,OSADETZ K G. Improving reservoir volumetric estimations in petroleum resource assessment using discovery process model[J]. Petroleum Science,2009,6:105-118. doi: 10.1007/s12182-009-0019-7 [8] GAO H Y,CHEN Z H,OSADETZ K G,et al. A pool-based model of the spatial distribution of undiscovered petroleum resoufrces[J]. Mathematical Geology,2000,32:725-749. doi: 10.1023/A:1007594423172 [9] LIU C L,CHARPENTIER R R ,SU J. Comparison of two methods used to model shape parameters of Pareto distributions[J]. Mathematical Geosciences,2011,43(7):847-859. doi: 10.1007/s11004-011-9361-6 [10] HOUGHTON J C. Use of the truncated shifted Pareto distribution in assessing size distribution of oil and gas fields[J]. Mathematical Geology,1988,20:907-937. doi: 10.1007/BF00892970 [11] 吴博,徐忠美. 基于图形法的油藏规模序列设计与实现:以四川盆地南部某气田为例[J]. 断块油气田,2016,23(2):197-209.WU B,XU Z M. Design and realization of reservoir size sequential method based on graphic:Taking one gas field in Sichuan Basin as an example[J]. Fault-Block Oil & Gas Field,2016,23(2):197-209. (in Chinese with English abstract [12] 谢寅符,马中振,刘亚明,等. 以成藏组合为核心的油气资源评价方法及应用:以巴西坎波斯(Campos)盆地为例[J]. 地质科技情报,2012,31(2):45-49.XIE Y F,MA Z Z,LIU Y M,et al. Method of play cored oil and gas resource assessment and application:Taking Campos Basin in Brazil as an example[J]. Geological Science and Technology Information,2012,31(2):45-49. (in Chinese with English abstract [13] 姜生玲,周庆华,李彦举,等. 油藏规模序列法在辽河滩海地区石油资源评价中的应用[J]. 陇东学院学报,2021,9(5):66-68.JIANG S L,ZHOU Q H,LI Y J,et al. Application of pool size sequence method to the prediction of petroleum resources in Tanhai area,Liaohe[J]. Journal of Longdong University,2021,9(5):66-68. (in Chinese with English abstract [14] 李婷,王韬,蒋文龙,等. 油藏规模序列法在玛湖凹陷低勘探程度区油气资源评价中的应用[J]. 特种油气藏,2021,28(5):60-67.LI T,WANG T,JIANG W L,et al. Application of reservoir scale sequence method in hydrocarbon resources assessment in the low-exploration area of Mahu Sag[J]. Special Oil & Gas Reservoirs,2021,28(5):60-67. (in Chinese with English abstract [15] 何敏,黄玉平,朱俊章,等. 珠江口盆地东部油气资源动态评价[J]. 中国海上油气,2017,29(5):1-11.HE M,HUANG Y P,ZHU J Z,et al. Dynamic evaluation of oil and gas resources in eastern Pearl River Mouth Basin[J]. China Offshore Oil and Gas,2017,29(5):1-11. (in Chinese with English abstract [16] SEIFERT D,JENSEN J L. Using sequential indicator simulation as a tool in reservoir description:Issues and uncertainties[J]. Mathematical Geology,1999,31:527-550. doi: 10.1023/A:1007563907124 [17] 石正勇,罗家群,金芸芸,等. 运用油藏规模序列法预测泌阳凹陷资源量[J]. 石油地质与工程,2017,31(1):62-65.SHI Z Y,LOU J Q,JIN Y Y,et al. Prediction of resource quantity in Biyang Depression using reservoir scale sequenc method[J]. Petrolum Geology and Engineering,2017,31(1):62-65. (in Chinese with English abstract [18] 姜振学,庞雄奇,周心怀,等. 油气资源评价的多参数约束改进油气田(藏)规模序列法及其应用[J]. 海相油气地质,2009,14(3):53-59.JIANG Z X,PANG X Q,ZHOU X H,et al. Multiparameter constrained reservoir size sequential method for petroleum resource estimation and the application[J]. Marine Origin Petroleum Geology,2009,14(3):53-59. (in Chinese with English abstract [19] POWER M. Lognormality in the observed size distribution of oil and gas pools as a consequence of sampling bias[J]. Mathematical Geology,1992,24:929-945. doi: 10.1007/BF00894659 [20] 赵旭东. 石油数学地质概论[M]. 北京:石油工业出版社,1992.ZHAO X D. Introduction to petroleum mathematics and geology[M]. Beijing:Petroleum Industry Press,1992. (in Chinese) [21] ATTANASI E D,DREW L J. Lognormal field size distributions as a consequence of economic truncation[J]. Journal of the International Association for Mathematical Geology,1985,17:335-351. doi: 10.1007/BF01032925 [22] STIGLIANO H,SINGH V,YEMEZ I,et al. Establishing minimum economic field size and analyzing its role in exploration-project risks assessment:A practical approach[J]. The Leading Edge,2016,35(2):180-189. doi: 10.1190/tle35020180.1 [23] 李晓光,鲁港,单俊峰. 油藏规模序列法的改进及应用[J]. 新疆石油地质,2009,30(1):106-108.LI X G,LU G,SHAN J F. Improvement and application of reservoir size sequential method[J]. Xinjiang Petroleum Geology,2009,30(1):106-108. (in Chinese with English abstract [24] 常宇,刘明洁,张庄,等. 四川盆地川西坳陷须三段砂岩储层致密化过程定量模拟[J]. 地质科技通报,2023,42(1):311-323.CHANG Y,LIU M J,ZHANG Z,et al. Quantitative simulation of the densification process of sandstone reservoir in the Xu 3 Member of Xujiahe Formation in Western Sichuan Depression,Sichuan Basin[J]. Bulletin of Geological Science and Technology,2023,42(1):311-323. (in Chinese with English abstract [25] 彭伟,舒逸,陈绵琨,等. 四川盆地复兴地区侏罗系凉高山组致密砂岩储层特征及其主控因素[J]. 地质科技通报,2023,42(3):102-113.PENG W,SHU Y,CHEN M K,et al. Tight sandstone reservoir characteristics and main controlling factors of Jurassic Lianggaoshan Formation in Fuxing area,Sichuan Basin[J]. Bulletin of Geological Science and Technology,2023,42(3):102-113. (in Chinese with English abstract [26] QIAO Y G,LIU Z G,LUO W,et al. Characterization of seismic information entropy attributes of braided river delta sedimentary microfacies for the Upper Shaximiao Formation in the Wubaochang area,northeastern Sichuan Basin,China[J]. Earth Science Informatics,2022,15:1371-1383. doi: 10.1007/s12145-021-00748-6 [27] LÜ,Z X,YE S J,YANG G,et al. Quantification and timing of porosity evolution in tight sand gas reservoirs:An example from the Middle Jurassic Shaximiao Formation,western Sichuan,China[J]. Petroleum Science,2015,12:207-217. doi: 10.1007/s12182-015-0021-1 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 792
- PDF下载量: 75
- 被引次数: 0
