Characterization model for the equivalent hydraulic aperture of a nonmatching fracture based on the MIC
-
摘要:
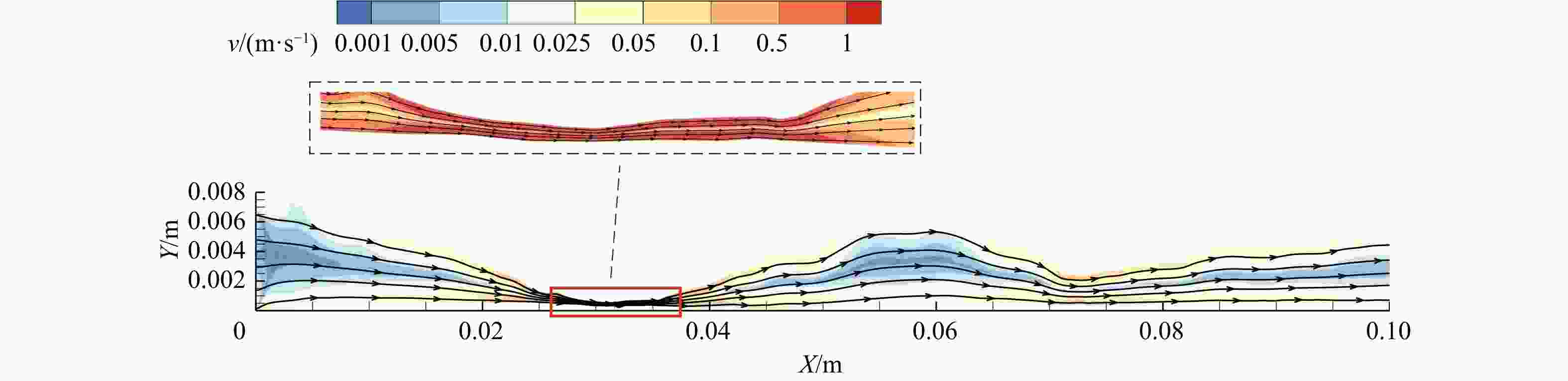
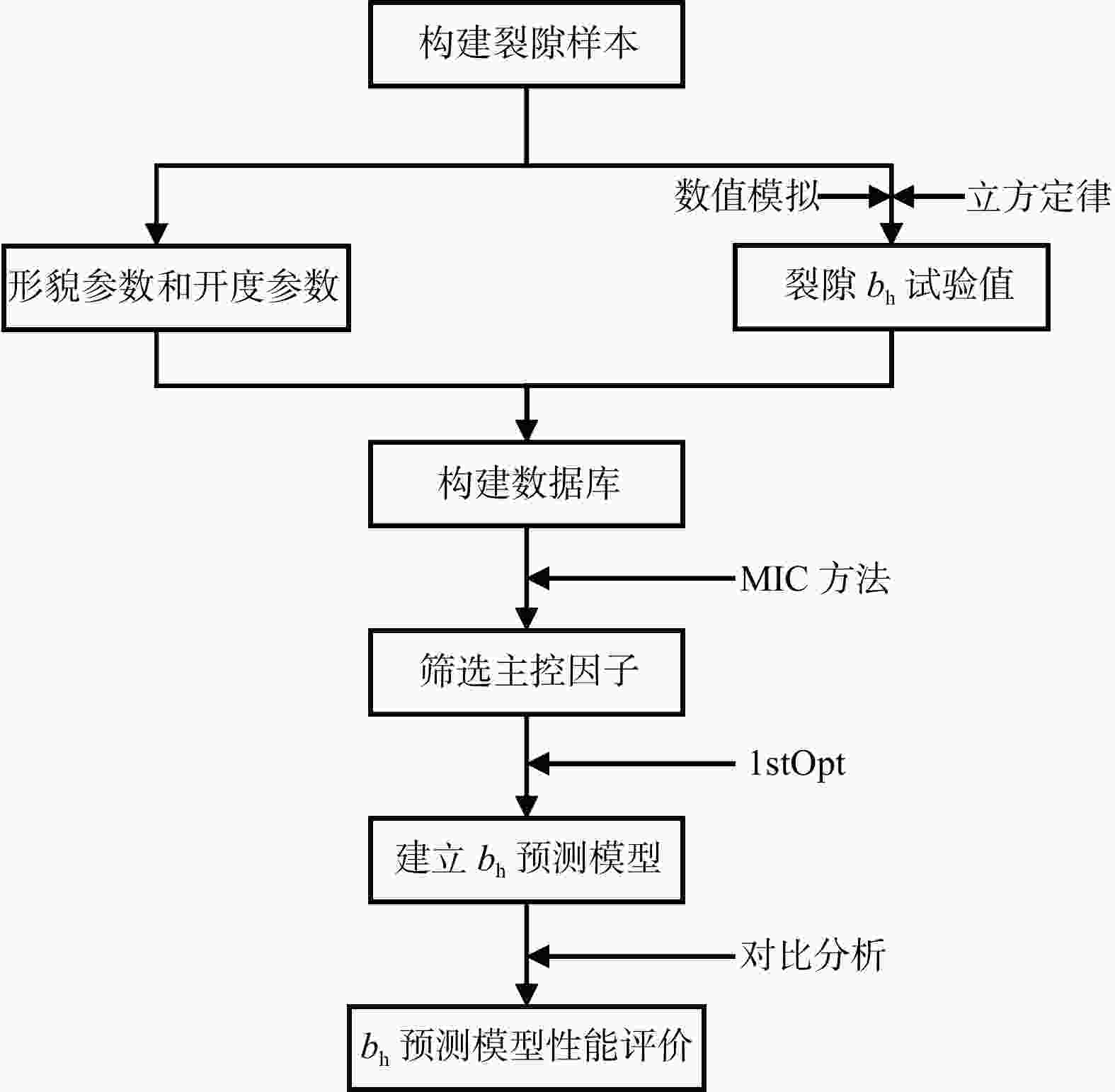
等效水力开度可以定量表征粗糙裂隙在达西流态下的导流能力,等效水力开度的精准预测对很多实际应用工程具有重要的意义。粗糙裂隙的等效水力开度受控于复杂的壁面形貌和开度分布等几何特征,综合考虑裂隙几何信息,通过最大互信息系数(MIC)的方法确定了等效水力开度的主控因子,并基于主控因子建立了粗糙裂隙等效水力开度的表征模型。首先,基于Barton 10条标准曲线构造了900组非吻合粗糙裂隙,通过壁面几何信息得到13个几何参数并采用数值模拟获取了所有裂隙的等效水力开度试验值,然后,采用最大互信息系数方法分析了等效水力开度与13个几何参数之间的相关性,共确定了4个主控因子,并基于主控因子建立了粗糙裂隙等效水力开度的表征模型。基于900个粗糙裂隙数据,选取已有的2个等效水力开度表征模型进行了对比分析。分析结果显示本研究提出的水力开度预测模型具有更好的表征性能。最后,研究了尺寸效应对建立等效水力开度表征模型的影响,并讨论了将该模型推广至三维裂隙的方法。
-
关键词:
- 粗糙裂隙 /
- 等效水力开度 /
- 壁面形貌 /
- 裂隙开度 /
- 最大互信息系数(MIC)
Abstract:Equivalent hydraulic aperture can quantitatively characterize hydraulic conductivity in rough fractures under Darcy flow conditions, making significance for various engineering applications.
Objective The equivalent hydraulic aperture of rough fractures is influenced by complex geometric features such as wall topography and aperture distribution. This study comprehensively considers fracture geometry, applies the maximal information coefficient (MIC) method to identify key factors influencing equivalent hydraulic aperture, and develops a characterization model based on it.
Methods 900 sets of nonmatching rough fractures were generated through Barton's 10 standard curves. Geometric information from fracture walls provided 13 parameters, and numerical simulations were used to obtain the equivalent hydraulic apertures. MIC considers the correlations between equivalent hydraulic aperture and 13 geometric parameters.
Results Four key factors were identified to form the basis of a characterization model for the equivalent hydraulic aperture of rough fractures.
Conclusion 900 rough fracture datasets validated the model's performance against two existing models, with the proposed model being more advanced than the current representations. The study also discussed the impact of size effects on hydraulic aperture models and the application for three-dimensional cases.
-
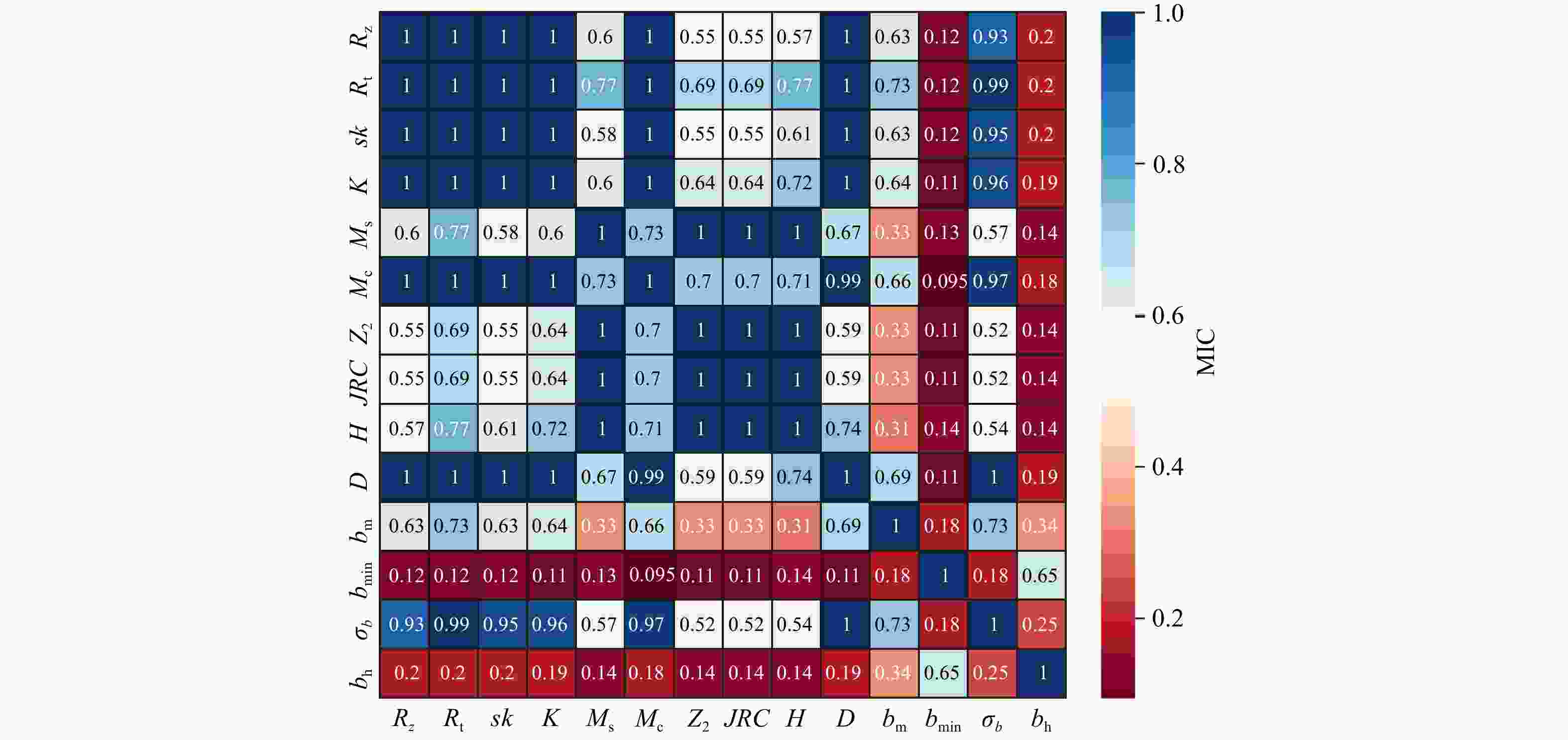
图 6 MIC分析结果(参数含义同表1)
Figure 6. MIC analysis results
表 1 等效水力开度预测方程
Table 1. Prediction equations for the equivalent hydraulic aperture
资料来源 表达式 方法 符号描述 PATIR等[10] ${b_{\text{h}}} = {b_{\text{m}}}{\left( {1 - 0.9{\xi ^{ - 0.56/{C_v}}}} \right)^{1/3}}$ 理论分析 bh为等效水力开度;bm为力学开度平均值;ξ为绝对突起高度;Cv为力学开度变异系数;Δb为力学开度增量;f为0.5~1.0之间的常数;$\eta $为经验常数;ε为裂隙表面积比常数;JRC为节理粗糙度系数;σb为力学开度均方根;τ为曲折系数;m为粗糙影响系数;JRC0为初始粗糙度系数;us为剪切位移;usp峰值处剪切位移;JRCmob为动粗糙度系数;Z2为一阶导数均方根;$\alpha '$为指数函数常数;L为二维粗糙裂隙剖面线的投影长度;D为分形维数;C为接触比;D*为相对分形维数;α和β均为拟合系数;Q为流量;R为粗糙度;(−αi+αi*)为拉格朗日乘子;Xi为支持向量;X为输入变量;A0/A为初级粗糙度归一化面积;C*为无量纲拟合参数;$ \sigma_\Pi $为次级粗糙度标准差;σc为静水压力;Re为雷诺数;t为时间;Be为充填隙宽,下同 WITHERSPOON等[11] ${b_{\text{h}}} = {b_{\mathrm{m}}} + f\Delta b$ 室内试验 WALSH[12] ${b_{\text{h}}} = {b_{\text{m}}}{\left[ {\left( {1 + \eta \varepsilon } \right)\left( {1 - \varepsilon } \right)} \right]^{ - 1/3}}$ 理论分析 BARTON等[13] ${b_{\text{h}}} = b_{\mathrm{m}}^2JR{C^{ - 2.5}}$ 室内试验 AMADEI等[14] ${b_{\text{h}}} = {b_{\text{m}}}{\left[ {1 + 0.6\left( {{\sigma _b}/{b_{\text{m}}}} \right)} \right]^{ - 1/3}}$ 数值模拟 RENSHAW[15] ${b_{\text{h}}} = {b_{\text{m}}}\exp \left( { - \sigma _b^2/2} \right)$ 理论分析 ZIMMERMAN等[16] $ {b_{\text{h}}} = {b_{\text{m}}}{\left[ {\left( {1 - 1.5\sigma _b^2/b_{\text{m}}^2} \right)\left( {1 - 2\varepsilon } \right)} \right]^{1/3}} $ 理论分析 WAITE等[17] $ {b_{\text{h}}} = {b_{\mathrm{m}}} \cdot {\tau ^{ - 1/3}} $ 理论分析 OLSSON等[18] $ \left\{ {\begin{array}{*{20}{l}} {{b_{\text{h}}} = b_{\text{m}}^2JRC_0^{ - 2.5},{u_{\mathrm{s}}} < 0.75{u_{{\mathrm{sp}}}}} \\ {{b_{\text{h}}} = b_{\text{m}}^{1/2}JR{C_{{\text{mob}}}},{u_{\mathrm{s}}} \geqslant {u_{{\mathrm{sp}}}}} \end{array}} \right. $ 室内试验 LIU[19] ${b_{\text{h}}} = {b_{\text{m}}}{\left[ {1 + \left( {\sigma _b^2/b_{\mathrm{m}}^2} \right)} \right]^{ - 1/2}}$ 理论分析 SCESI等[20] $ {b_{\text{h}}} = b_{\mathrm{m}}^{2/3}{\left[ {1 + 8.8\left( {0.5 - {b_{\mathrm{m}}}/2JR{C^{2.5}}} \right)} \right]^{ - 1/2}} $ 理论分析 QIAN等[21] ${b_{\text{h}}} = {b_{\mathrm{m}}}{\left( {\tau \cdot m} \right)^{1/3}}$ 理论分析 LI等[22] $ \left\{ {\begin{array}{*{20}{l}} {{b_{\text{h}}} = \dfrac{{{b_{\mathrm{m}}}}}{{1 + Z_2^{2.25}}},{Re} < 1} \\ {{b_{\text{h}}} = \dfrac{{{b_{\mathrm{m}}}}}{{1 + Z_2^{2.25} + \left( {6 \times {{10}^{ - 5}} + 4 \times {{10}^{ - 3}}} \right)\left( {{Re} - 1} \right)}},{Re} \geqslant 1} \end{array}} \right. $ 数值模拟 LIU等[23] ${b_{\text{h}}} = {\left( {4/\pi \alpha '} \right)^{4 - 2{D}}}{L^{{D} - 1}}$ 理论分析 ZOORABADI等[24] ${b_{\text{h}}} = {b_{\mathrm{m}}}\left( {0.991\ 2 - 4.53 \times {{10}^{ - 6}} \times JR{C^{3.303}}} \right)$ 室内试验 XIE等[25] $ {b_{\text{h}}} = {b_{\text{m}}}{\left[ {0.94 - 5{{\left( {{\sigma _b}/{b_{\mathrm{m}}}} \right)}^2}} \right]^{1/3}} $ 数值模拟 王报等[26] ${b_{\text{h}}} = {b_{\mathrm{m}}}\left( {0.991\ 2 - 1.525 \times {{10}^{ - 6}}JR{C^{3.76}}} \right)$ 数值模拟 CHEN等[27] $ {b_{\text{h}}} = {b_{\mathrm{m}}}{\left( {1 - 1.1C} \right)^4}{\left( {1 + 2/{D^*}} \right)^{3/5}} $ 室内试验 CAO等[28] $ \left\{ {\begin{array}{*{20}{l}} {{b_{\text{h}}} = \alpha + \beta {b_{\mathrm{m}}},{u_{\mathrm{s}}} < {u_{{\mathrm{sp}}}}} \\ {{b_{\text{h}}} = \alpha {e^{\beta {b_{\mathrm{m}}}}},{u_{\mathrm{s}}} \geqslant {u_{{\mathrm{sp}}}}} \end{array}} \right. $ 室内试验 鲁俊杰[29] $ {b_{\text{h}}} = {b_{\text{m}}}\left[ {1 - {\text{exp}}\left( { - 0.388\ 96{b_{\mathrm{m}}}/{\sigma _b}} \right)} \right] $ 室内试验 XIAO等[30] $ \begin{aligned} {b_{\text{h}}} = &\left( { - 0.327Q + 0.5} \right) + \left( {0.311Q - 0.5} \right) \cdot {\sigma _b} + \\ &\left( {0.144Q - 0.232} \right) \cdot R + \left( { - 0.546Q + 0.761} \right) \cdot {b_{\mathrm{m}}} \end{aligned} $ 数值模拟 SUN等[31] $ {b_{\text{h}}} = \displaystyle\sum\limits_{i = 1}^{206} {\left( { - {\alpha _i} + \alpha _i^*} \right){{\mathrm{e}}^{ - 0.939\left\| {{X_i},X} \right\|}} + 0.247\ 3} $ 数值模拟 TAN等[32] $ {b_{\text{h}}} = {\left[ {{A_0}/A\left( {1 - 1/{C^*}} \right)} \right]^{0.4}}\left[ {{b_{\mathrm{m}}} - 1.7\left( {\sigma _\Pi ^2/{b_{\mathrm{m}}}} \right)} \right] $ 理论分析 YIN等[33] $ {b_{\text{h}}} = {b_{\mathrm{m}}}\exp \left( { - 0.686\ 5Z_2^{0.579\ 8}/b_{\mathrm{m}}^{ - 0.887\ 6}} \right) $ 室内试验 赵鹏等[34] $ {b_{\text{h}}} = 16.7 + 72.54\exp \left( { - {\sigma _{\mathrm{c}}}/10.2} \right) $ 室内试验 ZHANG等[35] $\begin{aligned} {b_{\text{h}}} = &0.177\ 3{Q^{ - 0.263\ 5}}\left( { - 0.307\ 1\ln \left( {{Z_2}} \right) + 1.428\ 7} \right)\times \\&\left( {0.133\ 3{b_{\mathrm{m}}} + 0.094\ 6} \right) \end{aligned} $ 数值模拟 甘磊等[36] $\begin{aligned} {b_{\text{h}}} =& { - 135.6B_{\text{e}}^2 + 24.332{B_{\mathrm{e}}} - 5.231\ 4} \ln t - \\ & {1\ 396.9B_{\text{e}}^2 - 185.86{B_{\mathrm{e}}} + 63.709} \end{aligned} $ 室内试验 表 2 不同模型预测性能对比结果
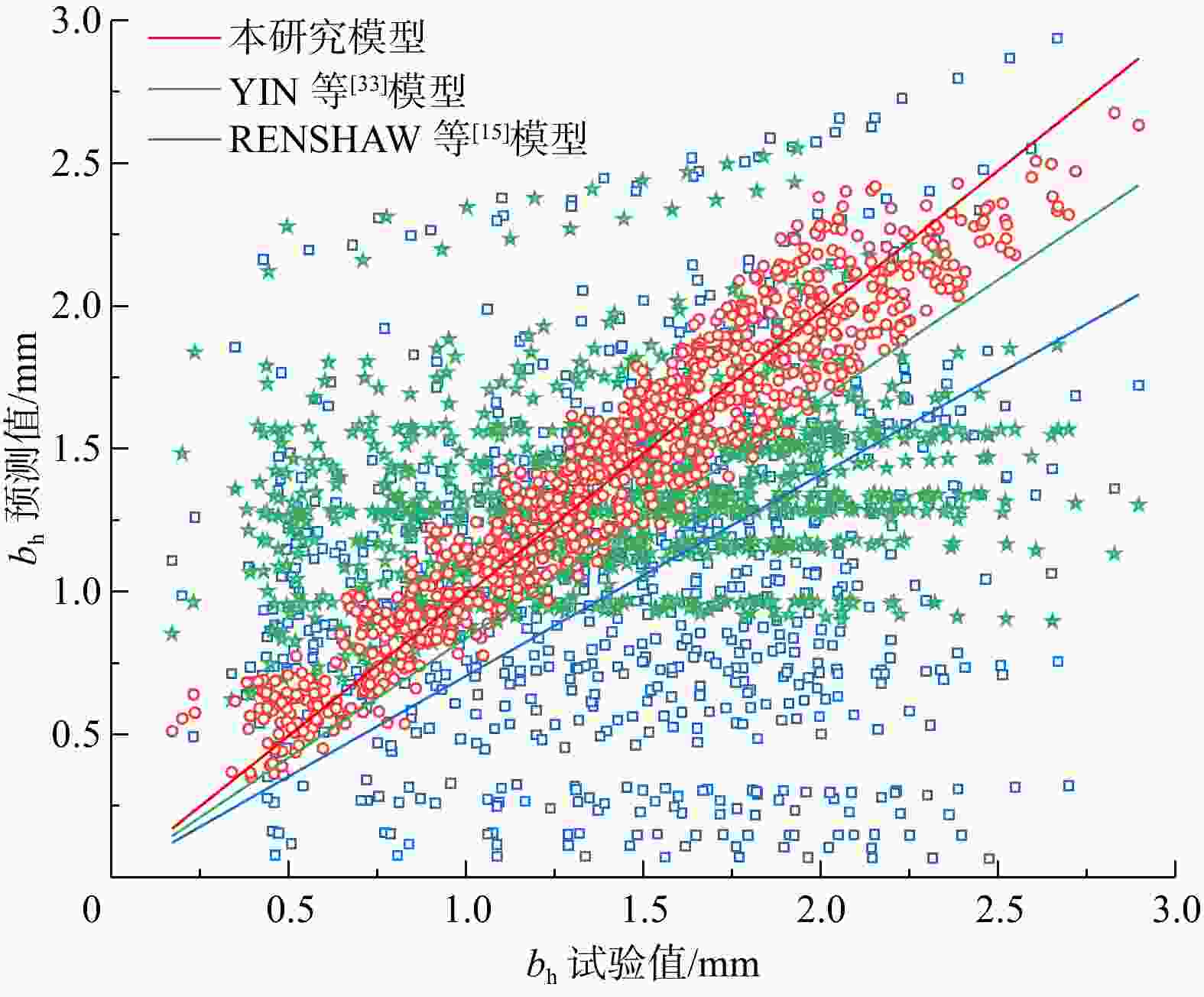
Table 2. Comparison result of the predictive performance of different models
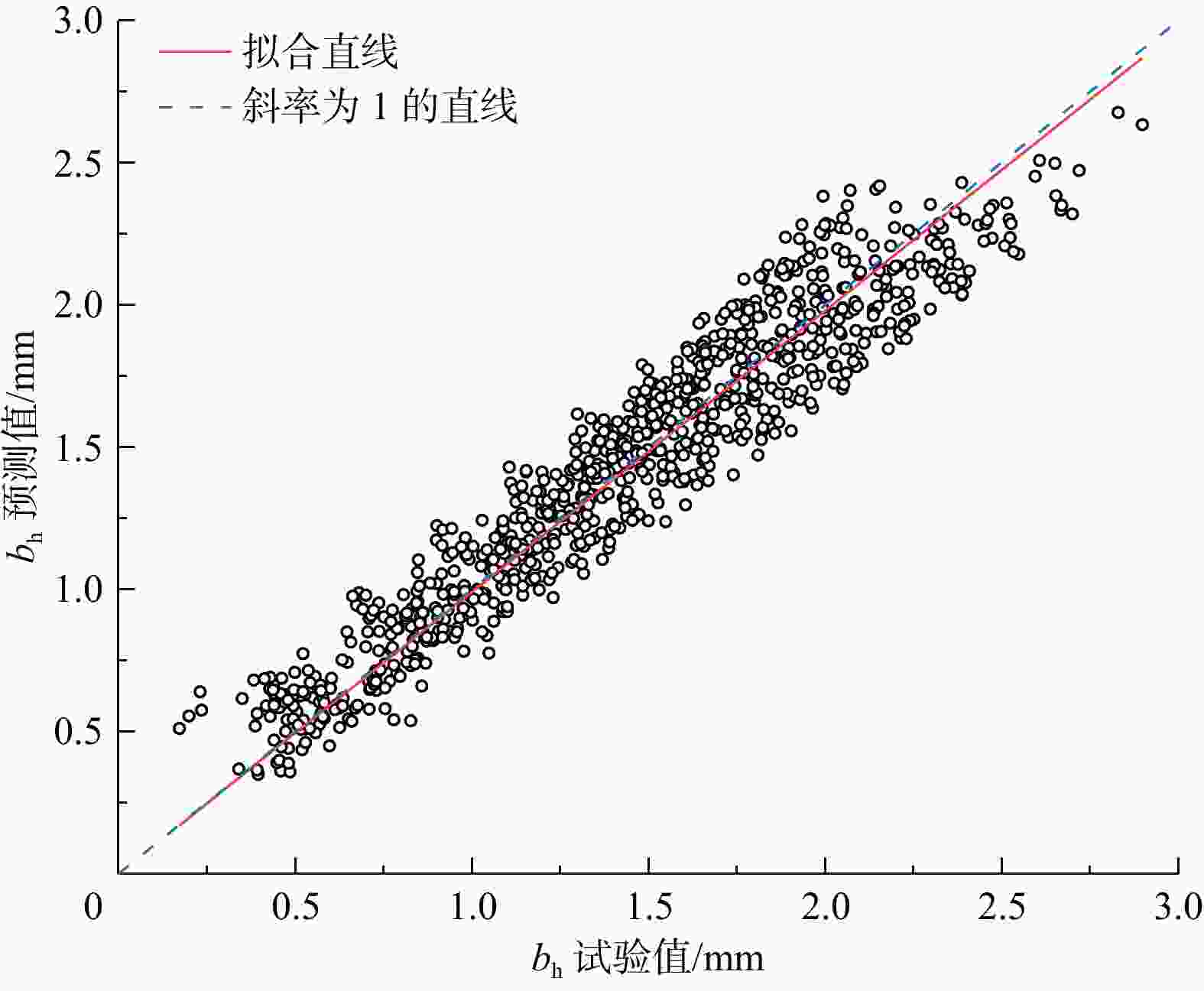
模型 预测公式 使用参数 NOF 本研究 $ {b_{\mathrm{h}}} = \left( {{Z_2} + 3.139} \right)\sqrt {{b_{\mathrm{m}}}{b_{{\mathrm{min}}}}} /\sqrt {5.469 + {R_{\mathrm{t}}}} $ Rt,Z2,bm,bmin 0.280 YIN等[33] $ {b_{\mathrm{h}}} = {b_{\mathrm{m}}}\exp \left( { - 0.686\ 5Z_2^{0.579\ 8}/b_{\mathrm{m}}^{ - 0.887\ 6}} \right) $ Z2,bm 0.531 RENSHAW[15] ${b_{\text{h}}} = {b_{\text{m}}}\exp \left( { - \sigma _b^2/2} \right)$ σb,bm 0.616 表 3 LIU等[44]裂隙模型的几何参数和水力参数
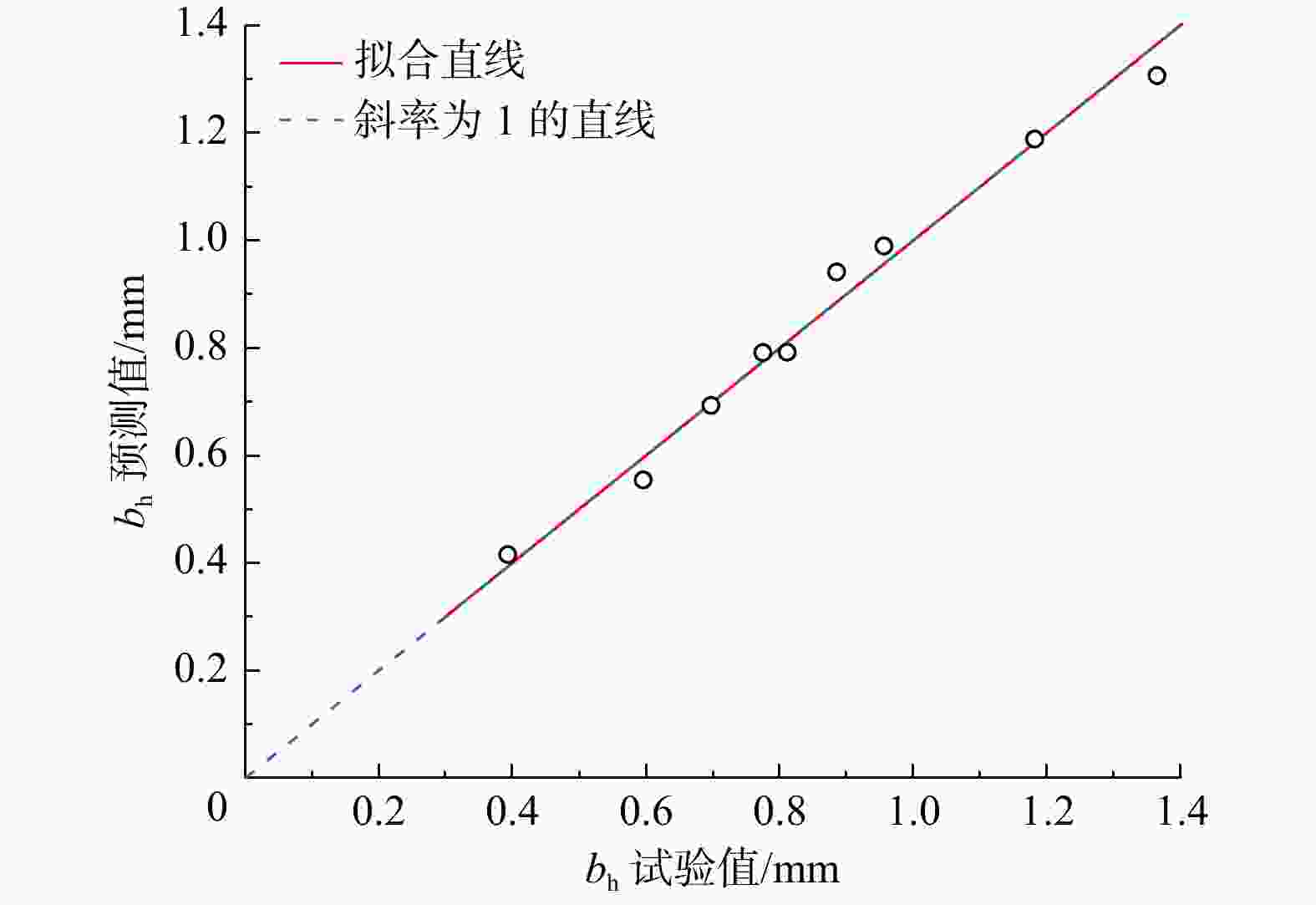
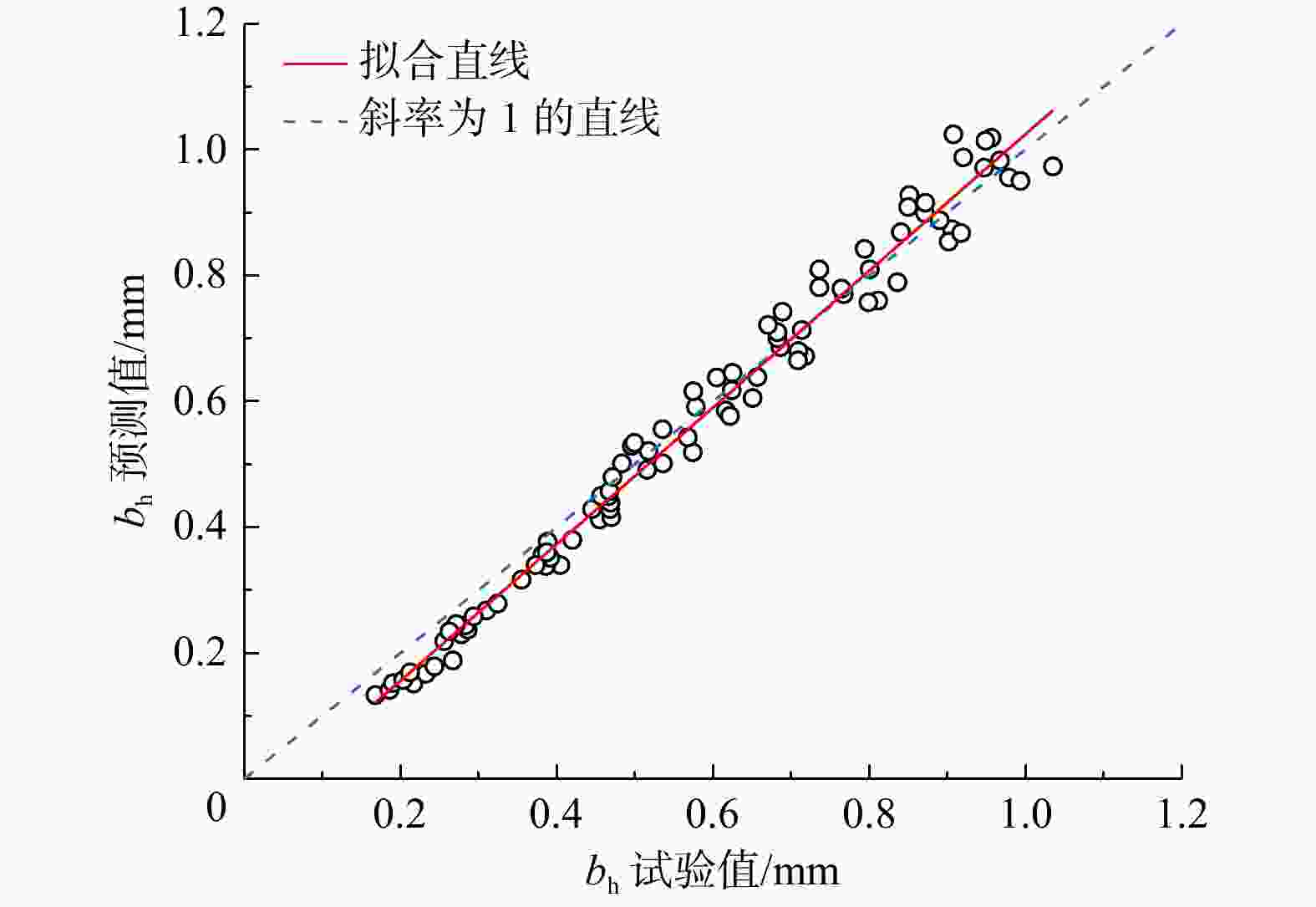
Table 3. Geometric and hydraulic parameters of the fracture model of LIU et al
模型序号 JRC 力学开度/mm bh试验值/mm bh预测值/mm 1 0~2 0.80 0.775 0.716 2 0~2 1.00 0.956 0.945 3 0~2 1.32 1.365 1.311 4 8~10 0.56 0.596 0.641 5 8~10 0.80 0.811 0.916 6 8~10 1.20 1.182 1.174 7 18~20 0.42 0.393 0.479 8 18~20 0.70 0.697 0.599 9 18~20 0.95 0.885 1.084 表 4 Synfrac软件生成裂隙的输入参数
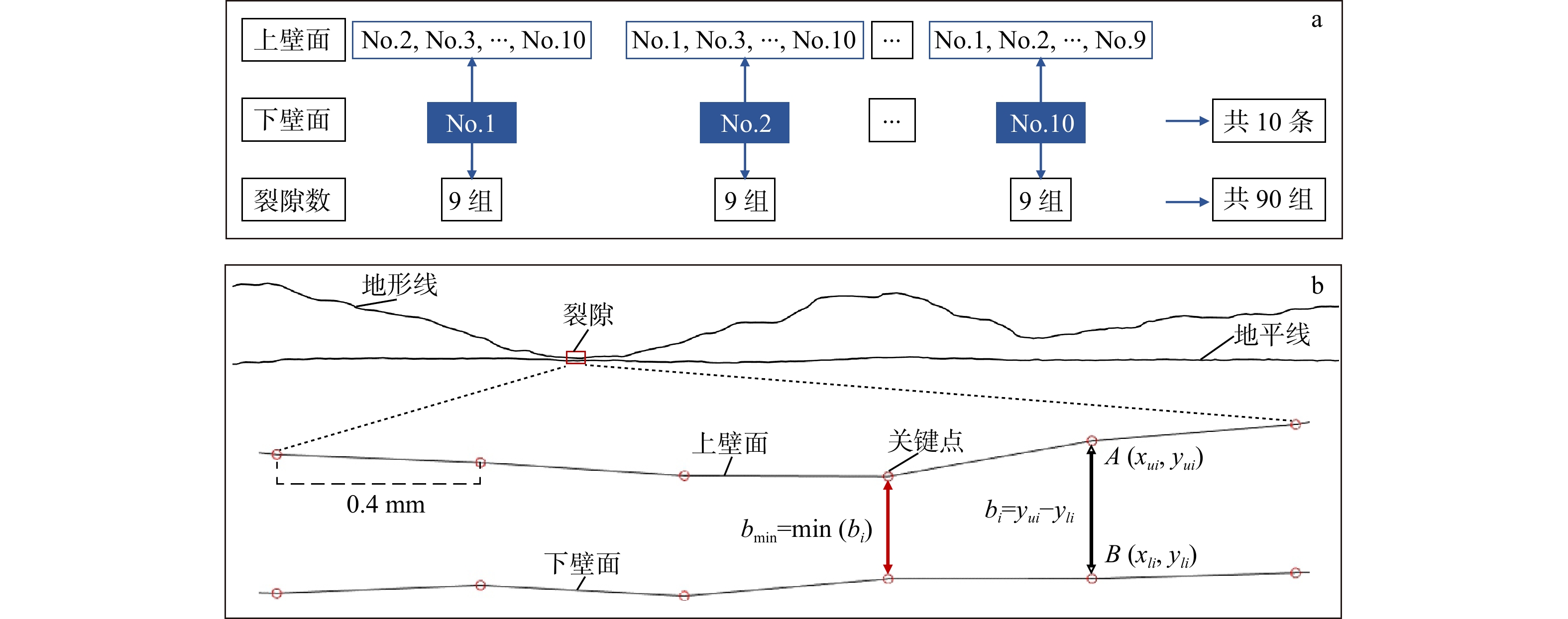
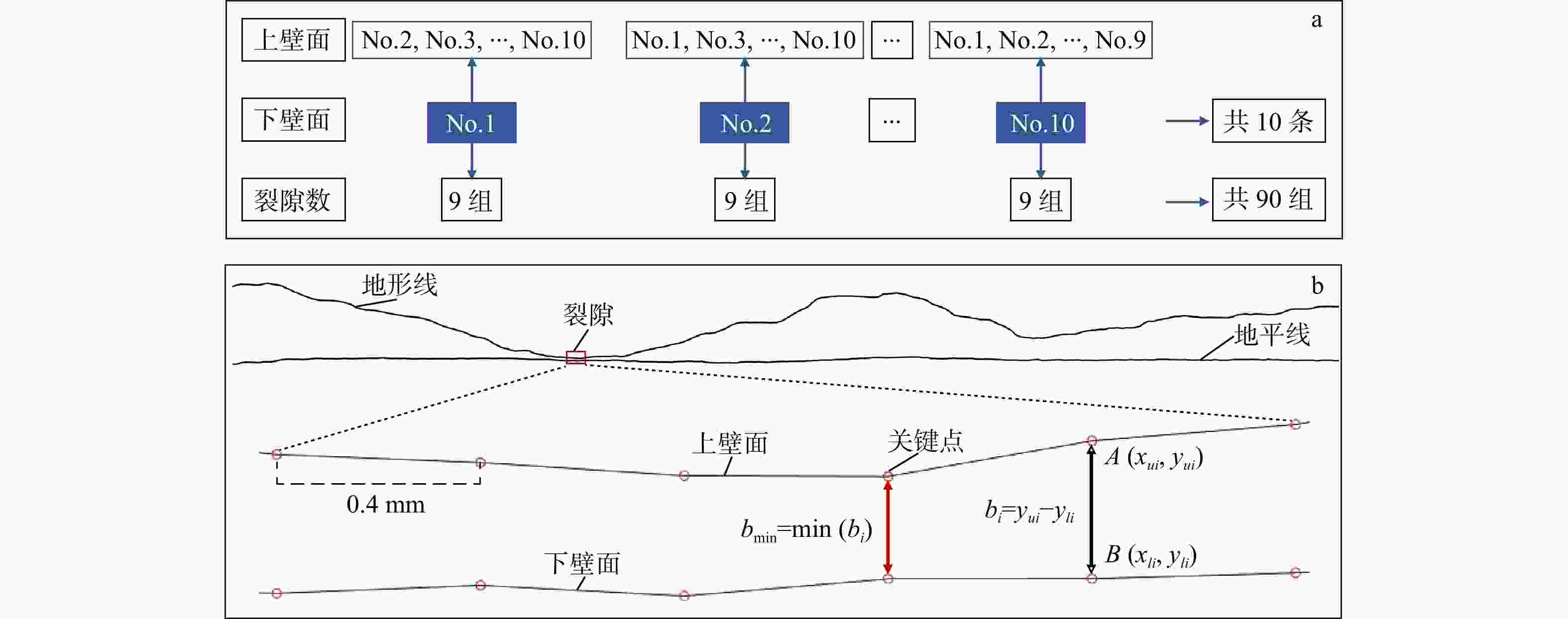
Table 4. Input parameters for fracture generation via Synfrac software
序号 L/mm ML TL/mm σb/mm WLmax WLmin D An 1 150 2.5 90 0.517 0.99 −0.06 2.1 1.07 2 200 2.5 90 0.617 0.99 −0.06 2.2 1.07 3 250 2.5 90 0.717 0.99 −0.06 2.3 1.07 注:L代表裂隙的物理尺寸;ML代表裂隙的不匹配波长;TL代表转变长度;σb代表力学开度标准差;WLmax代表最大匹配因子;WLmin代表最小匹配因子;D代表分形维数;An代表各向异性系数 -
[1] TANG H M,WASOWSKI J,JUANG C H. Geohazards in the Three Gorges Reservoir area,China:Lessons learned from decades of research[J]. Engineering Geology,2019,261:105267. doi: 10.1016/j.enggeo.2019.105267 [2] CHRISTENSEN M,TANINO Y. Enhanced permeability due to apparent oil/brine slippage in limestone and its dependence on wettability[J]. Geophysical Research Letters,2017,44(12):6116-6123. doi: 10.1002/2017GL073603 [3] 胡成,陈刚,曹孟雄,等. 基于离散裂隙网络法和水流数值模拟技术的地下水封洞库水封性研究[J]. 地质科技通报,2022,41(1):119-126.HU C,CHEN G,CAO M X,et al. A case study on water sealing efficieny of groundwater storage caverns using discrete fracture network method and flow numerical simulation[J]. Bulletin of Geological Science and Technology,2022,41(1):119-126. (in Chinese with English abstract [4] 梁劲,王强,胡新丽,等. 渗流-应力耦合下侏罗系红砂岩力学及渗透特性试验研究[J]. 地质科技通报,2023,42(1):52-61.LIANG J,WANG Q,HU X L,et al. Experimental study on mechanics and permeability characteristics of Jurassic red sandstone under hydro-mechanical coupling[J]. Bulletin of Geological Science and Technology,2023,42(1):52-61. (in Chinese with English abstract [5] 赵军,闫文雯,徐通,等. 朝阳沟阶地扶杨油层微观孔隙结构及渗流机理分析[J]. 地质科技通报,2023,42(2):194-206.ZHAO J,YAN W W,XU T,et al. Analysis of microscopic pore structure and seepage mechanism of the Fuyang oil reservoir in Chaoyanggou terrace[J]. Bulletin of Geological Science and Technology,2023,42(2):194-206. (in Chinese with English abstract [6] BEAR J. Dynamics of fluids in porous media[M]. [S. l. ]:American Elsevier Publishing Company,1972. [7] ZIMMERMAN R W,BODVARSSON G S. Hydraulic conductivity of rock fractures[J]. Transport in Porous Media,1996,23(1):1-30. [8] 周佳庆. 裂隙介质非线性渗流与非费克传输的宏细观机制研究[D]. 武汉:武汉大学,2018.ZHOU J Q. Mechanisms of nonlinear flow and anomalous transport in fractured media:From micro- to macro-scale[D]. Wuhan:Wuhan University,2018. (in Chinese with English abstract [9] 孙自豪. 岩石裂隙非线性渗流特性表征及应用[D]. 武汉:中国地质大学,2021.SUN Z H. Characterization and application of nonlinear flow in rock fractures[D]. Wuhan:China University of Geosciences(Wuhan),2021. (in Chinese with English abstract [10] PATIR N,CHENG H S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication[J]. Journal of Lubrication Technology,1978,100(1):12-17. doi: 10.1115/1.3453103 [11] WITHERSPOON P A,WANG J S Y,IWAI K,et al. Validity of cubic law for fluid flow in a deformable rock fracture[J]. Water Resources Research,1980,16(6):1016-1024. doi: 10.1029/WR016i006p01016 [12] WALSH J B. Effect of pore pressure and confining pressure on fracture permeability[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstrats,1981,18(5):429-435. [13] BARTON N,BANDIS S,BAKHTAR K. Strength,deformation and conductivity coupling of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1985,22(3):121-140. [14] AMADEI B,ILLANGASEKARE T. A mathematical model for flow and solute transport in non-homogeneous rock fractures[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1994,31(6):719-731. [15] RENSHAW C E. On the relationship between mechanical and hydraulic apertures in rough-walled fractures[J]. Journal of Geophysical Research (Solid Earth),1995,100(B12):24629-24636. doi: 10.1029/95JB02159 [16] ZIMMERMAN R W,BODVARSSON G S. Hydraulic conductivity of rock fractures[J]. Transport in Porous Media,1996,23(1):121-140. [17] WAITE M E,GE S,SPETZLER H. A new conceptual model for fluid flow in discrete fractures:An experimental and numerical study[J]. Journal of Geophysical Research (Solid Earth),1999,104(6):13049-13059. [18] OLSSON R,BARTON N. An improved model for hydromechanical coupling during shearing of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences,2001,38(3):317-329. doi: 10.1016/S1365-1609(00)00079-4 [19] LIU E. Effects of fracture aperture and roughness on hydraulic and mechanical properties of rocks:Implication of seismic characterization of fractured reservoirs[J]. Journal of Geophysics and Engineering,2005,2(1):38-47. doi: 10.1088/1742-2132/2/1/006 [20] SCESI L,GATTINONI P. Roughness control on hydraulic conductivity in fractured rocks[J]. Hydrogeology Journal,2007,15(2):201-211. doi: 10.1007/s10040-006-0076-6 [21] QIAN C X,HUANG B,WANG Y J,et al. Water seepage flow in concrete[J]. Construction and Building Materials,2012,35:491-496. doi: 10.1016/j.conbuildmat.2012.04.043 [22] LI B,JIANG Y J. Quantitative estimation of fluid flow mechanism in rock fracture :Taking into account the influences of JRC and reynolds number[J]. Journal of MMIJ,2013,129(7):479-484. [23] LIU R C,JIANG Y J,LI B,et al. A fractal model for characterizing fluid flow in fractured rock masses based on randomly distributed rock fracture networks[J]. Computers and Geotechnics,2015,65:45-55. doi: 10.1016/j.compgeo.2014.11.004 [24] ZOORABADI M,SAYDAM S,TIMMS W,et al. Non-linear flow behaviour of rough fractures having standard JRC profiles[J]. International Journal of Rock Mechanics and Mining Sciences,2015,76:192-199. doi: 10.1016/j.ijrmms.2015.03.004 [25] XIE L Z,GAO C,REN L,et al. Numerical investigation of geometrical and hydraulic properties in a single rock fracture during shear displacement with the Navier-Stokes equations[J]. Environmental Earth Sciences,2015,73(11):7061-7074. doi: 10.1007/s12665-015-4256-3 [26] 王报,王媛,牛玉龙. 基于离散标准节理粗糙度系数曲线的粗糙单裂隙等效水力隙宽的确定[J]. 水电能源科学,2017,35(4):77-80.WANG B,WANG Y,NIU Y L. Determination on hydraulic aperture of single rough fractures based on standard curves of discrete joint roughness coefficient[J]. Water Resources and Power,2017,35(4):77-80. (in Chinese with English abstract [27] CHEN Y D,LIANG W G,LIAN H J,et al. Experimental study on the effect of fracture geometric characteristics on the permeability in deformable rough-walled fractures[J]. International Journal of Rock Mechanics and Mining Sciences,2017,98:121-140. doi: 10.1016/j.ijrmms.2017.07.003 [28] CAO C,XU Z G,CHAI J R,et al. Radial fluid flow regime in a single fracture under high hydraulic pressure during shear process[J]. Journal of Hydrology,2019,579:124142. doi: 10.1016/j.jhydrol.2019.124142 [29] 鲁俊杰. 花岗岩裂隙等效水力隙宽表征及渗透特性研究[D]. 南京:南京大学,2019.LU J J. Research on characterization of equivalent hydraulic aperture and permeability in fractures of granite[D]. Nanjing:Nanjing University,2019. (in Chinese with English abstract [30] XIAO F,ZHAO Z Y. Evaluation of equivalent hydraulic aperture (EHA) for rough rock fractures[J]. Canadian Geotechnical Journal,2019,56(10):1486-1501. doi: 10.1139/cgj-2018-0274 [31] SUN Z H,WANG L Q,ZHOU J Q,et al. A new method for determining the hydraulic aperture of rough rock fractures using the support vector regression[J]. Engineering Geology,2020,271:105618. doi: 10.1016/j.enggeo.2020.105618 [32] TAN J,RONG G,ZHAN H B,et al. An innovative method to evaluate hydraulic conductivity of a single rock fracture based on geometric characteristics[J]. Rock Mechanics and Rock Engineering,2020,53(10):4767-4786. doi: 10.1007/s00603-020-02196-y [33] YIN P J,ZHAO C,MA J J,et al. Experimental study of non-linear fluid flow though rough fracture based on fractal theory and 3D printing technique[J]. International Journal of Rock Mechanics and Mining Sciences,2020,129:104293. doi: 10.1016/j.ijrmms.2020.104293 [34] 赵鹏,冯子军,南翰墨,等. 花岗岩干热岩体裂隙的大位移动态剪切-渗流特征[J]. 煤炭学报,2023,48(3):1139-1154.ZHAO P,FENG Z J,NAN H M,et al. Characteristics of large-displacement based dynamic shearing-flow through the fractures in the granitic hot dry rock mass[J]. Journal of China Coal Society,2023,48(3):1139-1154. (in Chinese with English abstract [35] ZHANG W,PENG Z,HAN C,et al. Numerical investigation of an equivalent hydraulic aperture for rough rock fractures based on cosimulation[J]. Computers and Geotechnics,2023,156:105281. doi: 10.1016/j.compgeo.2023.105281 [36] 甘磊,金洪杰,沈振中,等. 不同粗糙度和充填隙宽下石灰岩裂隙渗流特性试验研究[J]. 岩石力学与工程学报,2023,42(增刊1):3415-3424.GAN L,JIN H J,SHEN Z Z,et al. Experimental investigation on seepage characteristics of limestone fractures with different roughness and filling gap width[J]. Chinese Journal of Rock Mechanics and Engineering,2023,42(S1):3415-3424. (in Chinese with English abstract [37] 汪旭. 基于机器学习的入侵检测研究[D]. 成都:西南交通大学,2020.WANG X. Research on intrusion detection based on machine learning[D]. Chengdu:Southwest Jiaotong University,2020. (in Chinese with English abstract [38] 朱道恒,李志强. 最大互信息系数的并行计算方法研究[J]. 科学技术与工程,2021,21(34):14625-14633. doi: 10.3969/j.issn.1671-1815.2021.34.023ZHU D H,LI Z Q. Parallel calculation method for maximum information coefficient[J]. Science Technology and Engineering,2021,21(34):14625-14633. (in Chinese with English abstract doi: 10.3969/j.issn.1671-1815.2021.34.023 [39] 余兴泓. 多维相关时序数据的预测方法研究[D]. 北京:北京工商大学,2021.YU X H. Research on forecasting methods of multi-dimensional correlated time series data[D]. Beijing:Beijing Technology and Business University,2021. (in Chinese with English abstract [40] DONG J B,JU Y. Quantitative characterization of single-phase flow through rough-walled fractures with variable apertures[J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources,2020,6(3):42. doi: 10.1007/s40948-020-00166-w [41] LI M,LIU X S,LI Y,et al. Effect of contact areas on seepage behavior in rough fractures under normal stress[J]. International Journal of Geomechanics,2022,22(4):04022019. doi: 10.1061/(ASCE)GM.1943-5622.0002330 [42] ZHU C,XU X D,WANG X T,et al. Experimental investigation on nonlinear flow anisotropy behavior in fracture media[J]. Geofluids,2019(9):1-9. [43] RASOULI V,HOSSEINIAN A. Correlations developed for estimation of hydraulic parameters of rough fractures through the simulation of JRC flow channels[J]. Rock Mechanics and Rock Engineering,2011,44(4):447-461. doi: 10.1007/s00603-011-0148-3 [44] LIU J,WANG Z C,QIAO L P,et al. Transition from linear to nonlinear flow in single rough fractures:Effect of fracture roughness[J]. Hydrogeology Journal,2021,29(3):1343-1353. doi: 10.1007/s10040-020-02297-6 [45] SUN Z H,WANG L Q,ZHOU J Q,et al. Prediction of the inertial permeability of a 2D single rough fracture based on geometric information[J]. Acta Geotechnica,2023,19(4):2105-2124. [46] BARTON N,CHOUBEY V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics and Rock Engineering,1977,10(1/2):1-54. [47] HEINZE T,FRANK S,WOHNLICH S. FSAT :A fracture surface analysis toolbox in MATLAB to compare 2D and 3D surface measures[J]. Computers and Geotechnics,2021,132:103997. [48] 范斌强. 基于精细雕刻的岩体结构面峰值抗剪强度模型及工程应用研究[D]. 武汉:中国地质大学(武汉),2021.FAN B Q. Research on the peak shear strength model of rock joint based on fine carving and its engineering application[D]. Wuhan:China University of Geosciences(Wuhan),2021. (in Chinese with English abstract [49] GUTJAHR T,HALE S,KELLER K,et al. Quantification of fracture roughness by change probabilities and hurst exponents[J]. Mathematical Geosciences,2022,54(4):679-710. doi: 10.1007/s11004-021-09985-3 [50] TSE R,CRUDEN D M. Estimating joint roughness coefficients[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1979,16(5):303-307. [51] VOSS R F. Fractals in nature:From characterization to simulation:The science of fractal images[M]. New York:Springer ,1988:21-70. [52] ODLING N E. Natural fracture profiles,fractal dimension and joint roughness coefficients[J]. Rock Mechanics and Rock Engineering,1994,27(3):135-153. doi: 10.1007/BF01020307 [53] 蒋宇静,李博,王刚,等. 岩石裂隙渗流特性试验研究的新进展[J]. 岩石力学与工程学报,2008,27(12):2377-2386. doi: 10.3321/j.issn:1000-6915.2008.12.001JIANG Y J,LI B,WANG G,et al. New advances in experimental study on seepage characteristics of rock fractures[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(12):2377-2386. (in Chinese with English abstract doi: 10.3321/j.issn:1000-6915.2008.12.001 [54] 喻亚奇. 岩体裂隙渗流立方定律修正及其工程应用[D]. 武汉:武汉大学,2022.YU Y Q. Corrected cubic law for rock fracture seepage and its engineering application[D]. Wuhan:Wuhan University,2022. (in Chinese with English abstract [55] 潘汝江. 多流态下粗糙单裂隙渗流规律研究[D]. 武汉:武汉轻工大学,2020.PAN R J. Research on the seepage law of rough single fracture in multi-flow state[D]. Wuhan:Wuhan Polytechnic University,2020. (in Chinese with English abstract [56] 何明翰. 基于结构化网格的CiADS绕丝定位燃料组件流动特性研究[D]. 北京:中国科学院大学,2022.HE M H. Study on flow characteristics of wire-wrapped fuel assembly in CiADS based on structured mesh[D]. Beijing:University of Chinese Academy of Sciences,2022. (in Chinese with English abstract [57] 孙志新. 湍流下颗粒滑移速度规律的数值模拟研究[D]. 北京:中国矿业大学,2021.SUN Z X. Numerical simulation research on particle slip velocity under turbulent flow[D]. Beijing:China University of Mining and Technology,2021. (in Chinese with English abstract [58] ZHOU J Q,HU S H,FANG S,et al. Nonlinear flow behavior at low Reynolds numbers through rough-walled fractures subjected to normal compressive loading[J]. International Journal of Rock Mechanics and Mining Sciences,2015,80:202-218. doi: 10.1016/j.ijrmms.2015.09.027 [59] ZHOU J Q,GAN F S,LI C,et al. A global inertial permeability for fluid flow in rock fractures:Criterion and significance[J]. Engineering Geology,2023,322:107167. doi: 10.1016/j.enggeo.2023.107167 [60] RESHEF D,RESHEF Y,FINUCANE H,et al. Detecting novel associations in large data sets[J]. Science,2011,334:1518-1524. doi: 10.1126/science.1205438 [61] 杨云凯. 基于互信息的过滤式特征选择算法研究[D]. 长春:吉林大学,2022.YANG Y K. Research on filtering feature selection algorithm based on mutual information[D]. Changchun:Jilin University,2022. (in Chinese with English abstract [62] SUN G L,LI J B,DAI J,et al. Feature selection for IoT based on maximal information coefficient[J]. Future Generation Computer Systems,2018,89:606-616. doi: 10.1016/j.future.2018.05.060 [63] CAO D,CHEN Y,CHEN J,et al. An improved algorithm for the maximal information coefficient and its application[J]. Royal Society Open Science,2021,8(2):201424. doi: 10.1098/rsos.201424 [64] LIU M,YANG Z,GUO Y,et al. MICAR:Nonlinear association rule mining based on maximal information coefficient[J]. Knowledge and Information Systems,2022,64(11):3017-3042. doi: 10.1007/s10115-022-01730-4 [65] SHI P,LI X,SHEN J N. Nonlinear modelling of selected micro- and macro-properties of weathered asphalt mixtures[J]. Construction and Building Materials,2020,253:119097. doi: 10.1016/j.conbuildmat.2020.119097 [66] MOUTSOPOULOS K N,PAPASPYROS I N E,TSIHRINTZIS V A. Experimental investigation of inertial flow processes in porous media[J]. Journal of Hydrology,2009,374(3/4):242-254. [67] YANG B,YANG T H,XU Z H,et al. Impact of particle-size distribution on flow properties of a packed column[J]. Journal of Hydrologic Engineering,2019,24(3):04018070. doi: 10.1061/(ASCE)HE.1943-5584.0001735 [68] ZHOU J Q,HU S H,CHEN Y F,et al. The friction factor in the Forchheimer equation for rock fractures[J]. Rock Mechanics and Rock Engineering,2016,49(8):3055-3068. doi: 10.1007/s00603-016-0960-x [69] OGILVIE S R,ISAKOV E,GLOVER P W J. Fluid flow through rough fractures in rocks. II:A new matching model for rough rock fractures[J]. Earth and Planetary Science Letters,2006,241(3/4):454-465. doi: 10.1016/j.jpgl.2005.11.041 -




 下载:
下载: