MLP-ANN model for predicting uniaxial compressive strength of rocks based on the rebound method
-
摘要:
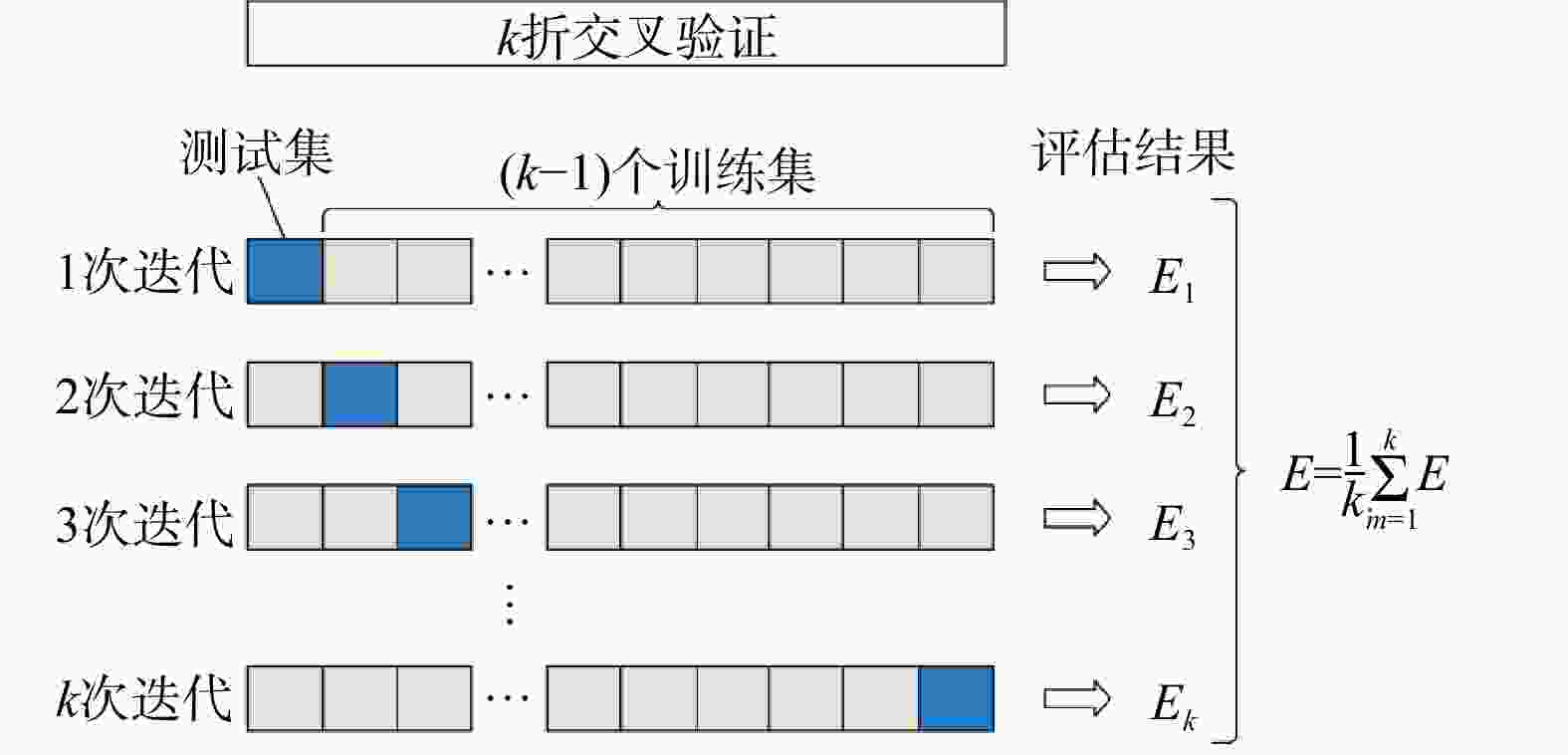
岩石单轴抗压强度是岩土工程中的重要参数，合理确定其数值对工程设计至关重要。本文提出了一种基于多层感知机的人工神经网络（MLP-ANN）模型，用于预测岩石单轴抗压强度。该模型以岩性、节理面、施密特锤回弹高度和纵波波速为输入参数，采用最大最小归一化进行参数标准化，并通过
k 折交叉验证提高模型的泛化能力。为优化模型性能，文章探讨了神经元数量、数据分割比例和激活函数对预测结果的影响。经对比验证，研究确定了最优模型配置：神经元数量为8，训练集与测试集比例为8∶2，激活函数选用Tanh函数。模型预测值与实际值对比分析结果表明，最优模型的平均绝对误差为3.500 MPa，均方根误差为5.836 MPa。结果表明，该模型预测误差较小，预测准确率较高，具有较好的实用性。Abstract:Objective The uniaxial compressive strength (UCS) of rock is an important parameter in geotechnical engineering, as well as accurately determining its value is crucial for engineering design.
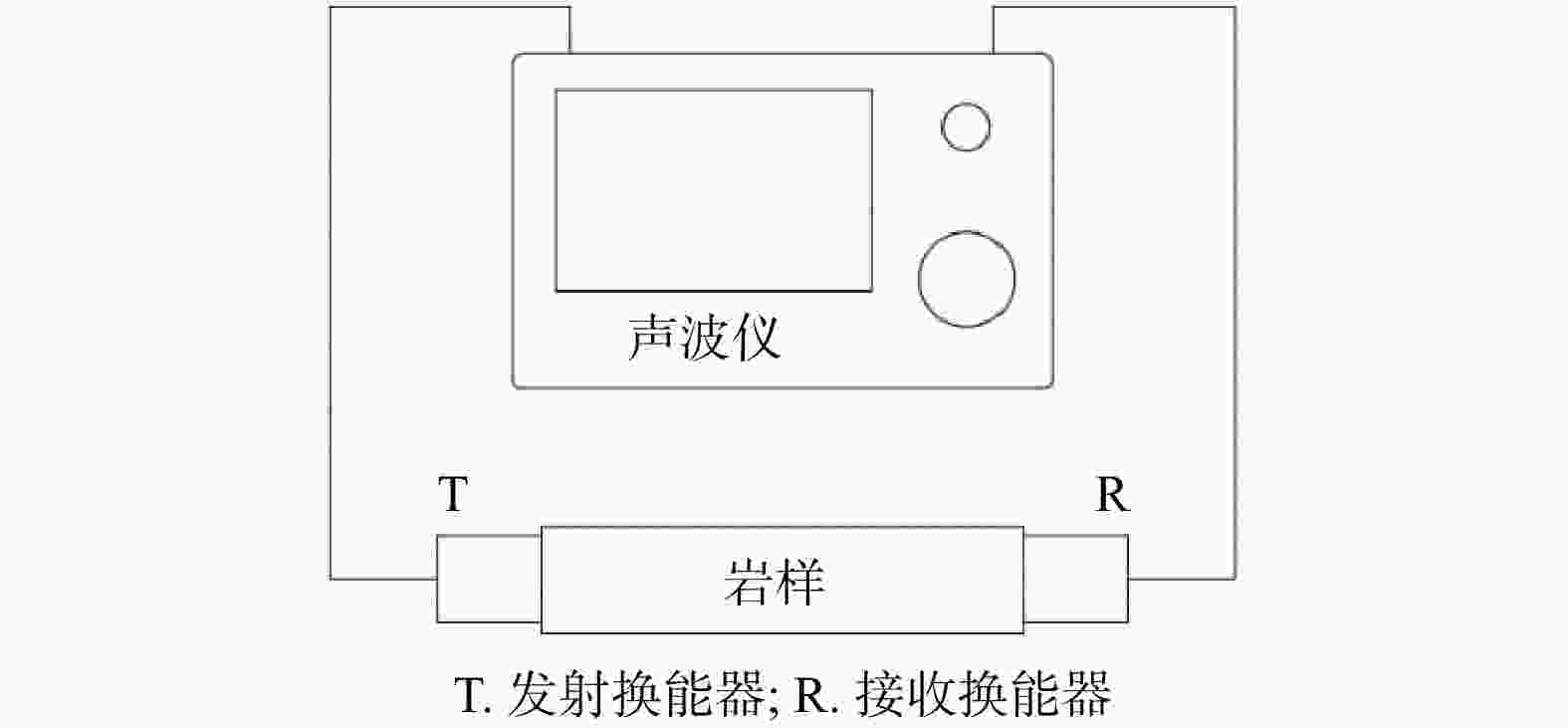
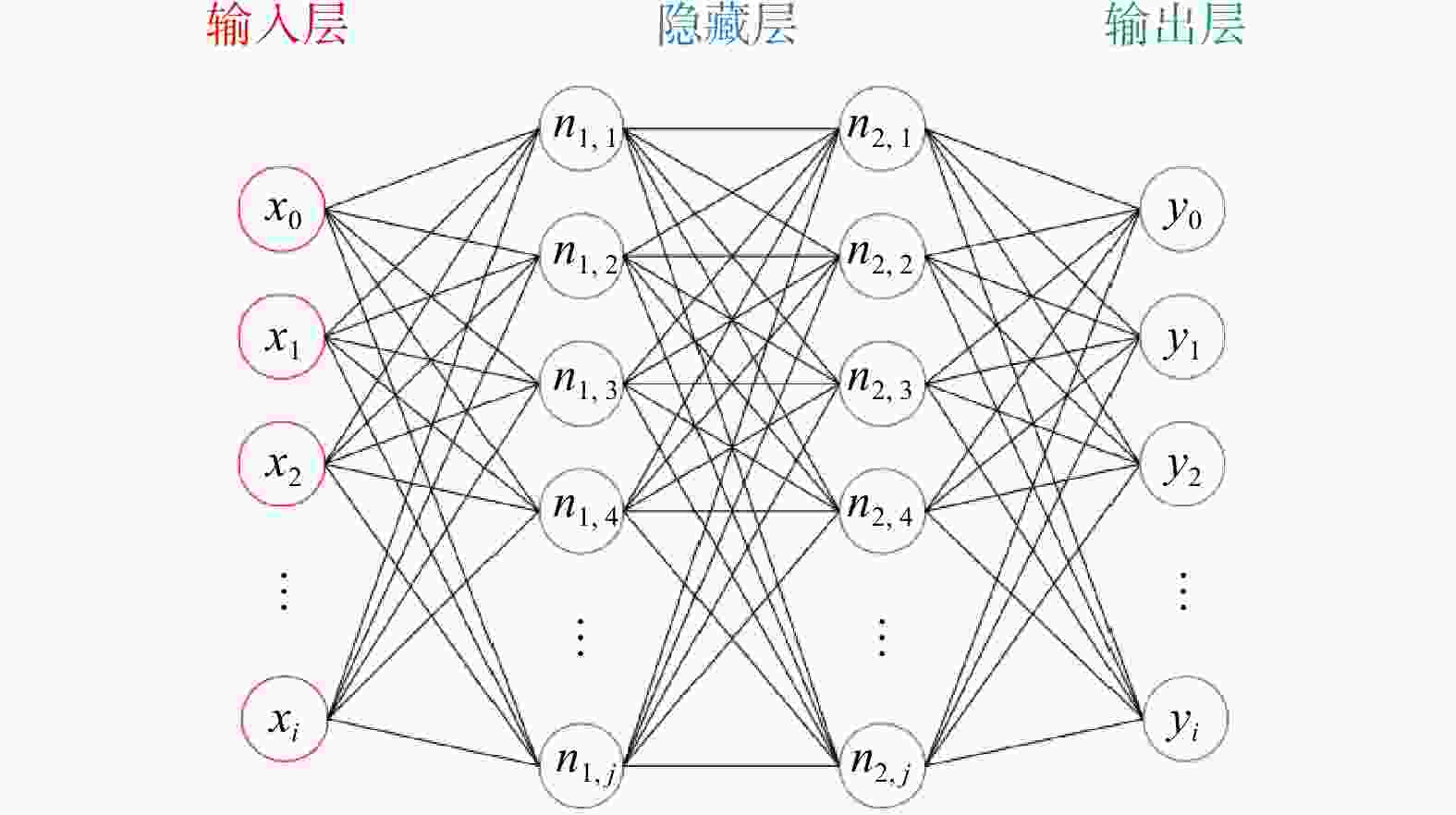
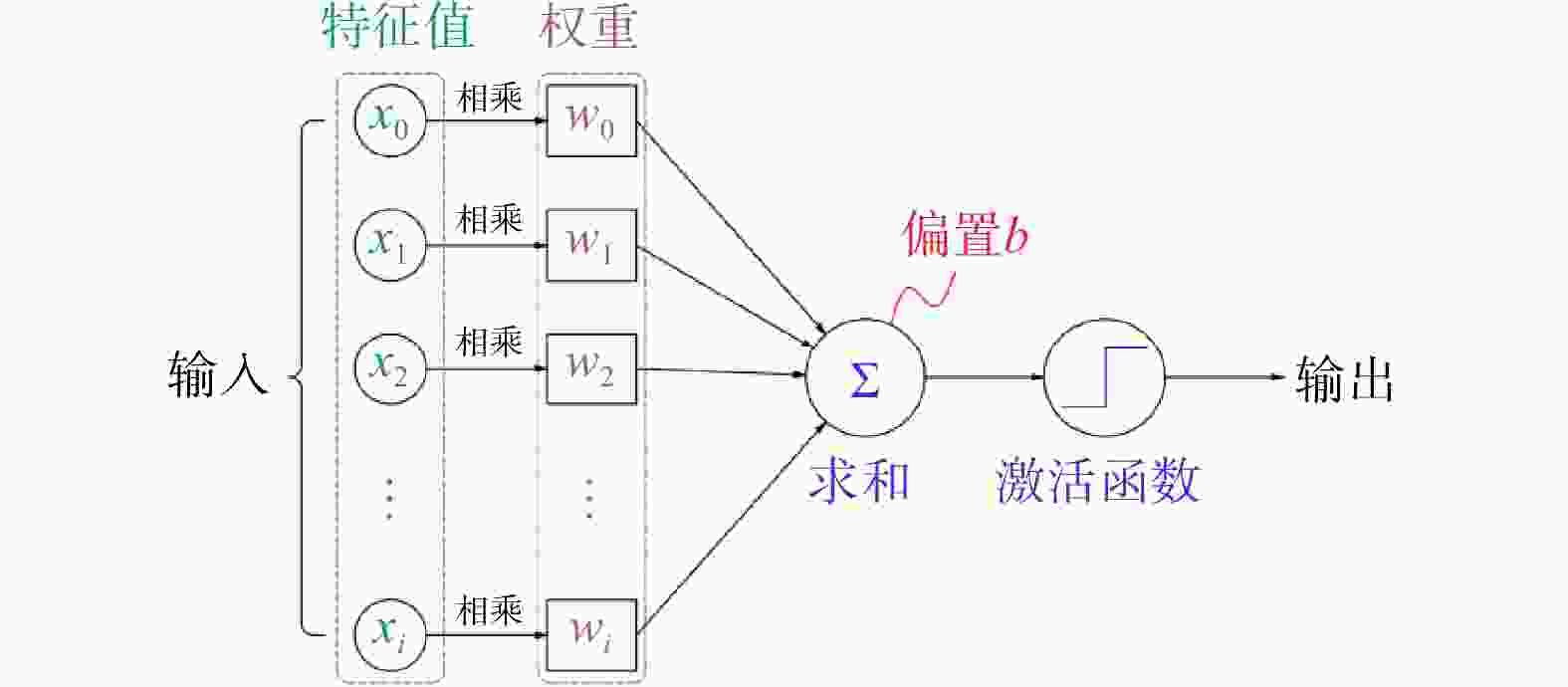
Methods This study proposed a machine learning model based on a multi-layer perceptron-Artificial Neural Network (MLP-ANN) to predict the UCS of rock. The model takes lithology, joint surfaces, Schmidt hammer rebound height, and P-wave velocity as input parameters, and applies min-max normalization to standardize these parameters. Additionally, k-fold cross-validation is used to improve the model’s generalization ability. To further optimize model performance, the paper explores the impact of the number of neurons, data splitting ratio, and activation function on prediction results.
Results Through comparative validation, the study determines the optimal model configuration: 8 neurons, a training-to-testing ratio of 8∶2, and the Tanh activation function. The comparison between predicted and actual values shows that the optimal model achieves an average absolute error of 3.500 MPa and a root mean square error of 5.836 MPa.
Conclusion These results indicate that the model has a small prediction error and high accuracy, illustrating good practicality.
-
图 6 MLP-ANN基本框架
xi为第i个输入变量；ni, j为第i层、第j个神经元；yi为第i个目标值
Figure 6. Basic framework of MLP-ANN
图 8 通过室内实验获取岩样相关参数（SRH、vp、 UCS）相对频率直方图和累计频率分布曲线
μg为平均值；q0为标准差
Figure 8. Histograms and cumulative distribution curves of parameters related to rock samples (SRH, vp, UCS) obtained by laboratory tests
图 10 不同激活函数损失变化图（隐藏层神经元数量=8）
Figure 10. Plot of loss variation with different activation functions (number of neurons in hidden layer = 8)
图 11 数据分割百分比对MLP-ANN预测性能影响
Figure 11. Effect of data segmentation percentage on MLP-ANN prediction performance
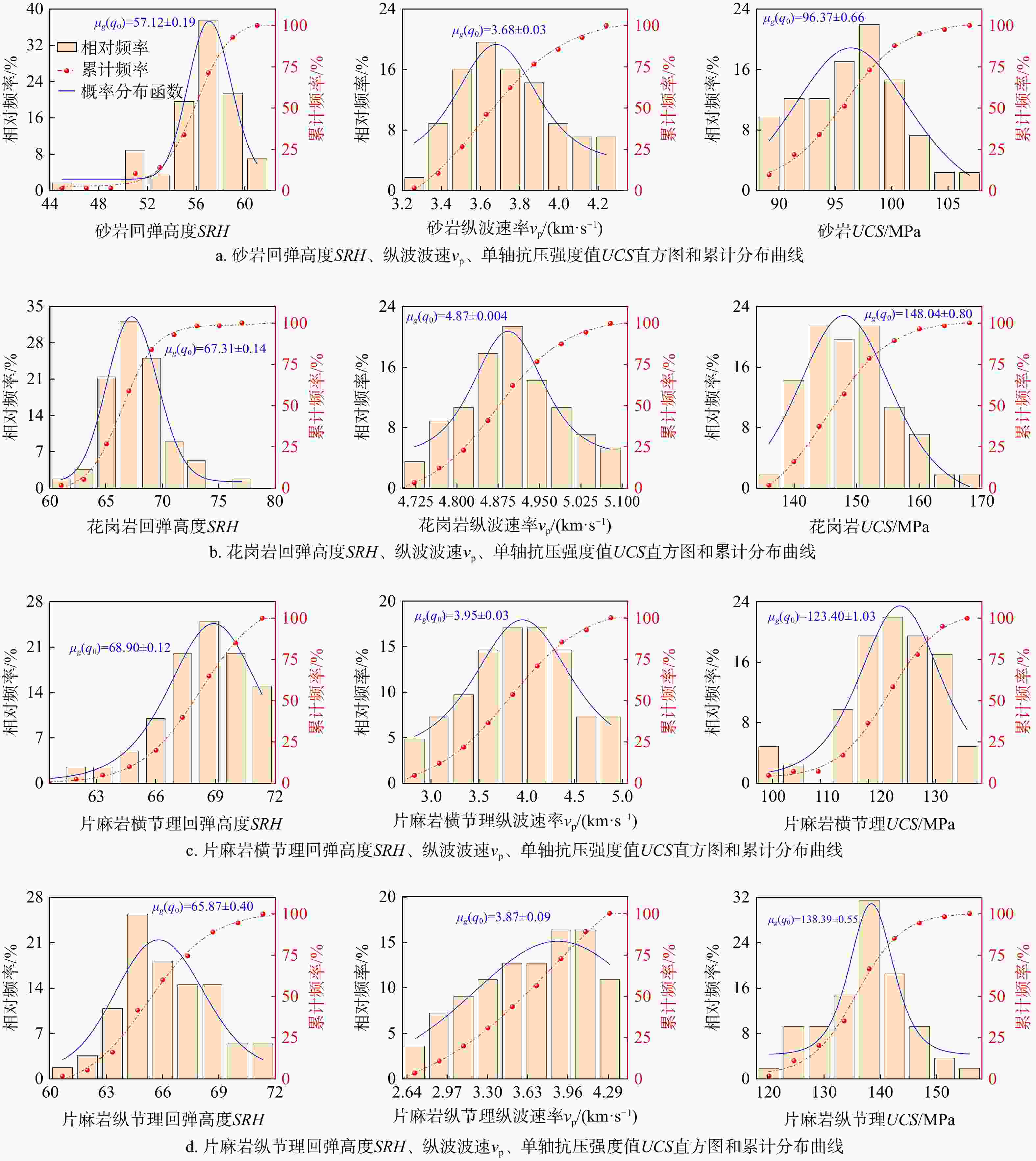
表 1 室内实验结果
Table 1. Results of experimental tests
岩性 数量 参数 最小值 平均值 中值 最大值 COV值/% 砂岩 56 ρ/(g·cm−3) 2.623 2.658 2.659 2.686 0.68 SRH 45.67 56.28 56.67 61.33 5.16 vp/(km·s−1) 3.319 3.747 3.718 4.287 6.66 μd 0.304 0.325 0.314 0.350 5.01 Ed/MPa 0.023 0.026 0.026 0.027 3.83 Gd/MPa 8.670 9.614 9.726 10.160 4.60 UCS/MPa 88.98 93.26 93.43 106.28 7.05 花岗岩 56 ρ/(g·cm−3) 2.780 2.788 2.787 2.794 0.09 SRH 60.67 67.43 67.33 76.33 3.92 vp/(km·s−1) 4.727 4.901 4.899 5.096 1.84 μd 0.347 0.361 0.359 0.381 2.89 Ed/MPa 0.037 0.040 0.039 0.042 3.80 Gd/MPa 13.576 14.470 14.192 15.674 4.70 UCS/MPa 134.33 148.88 149.06 168.59 4.57 片麻岩横节理 41 ρ/(g·cm−3) 2.639 2.652 2.653 2.655 0.12 SRH 62.33 68.24 68.67 72.00 3.27 vp/(km·s−1) 2.762 3.899 3.911 4.936 13.91 μd 0.336 0.356 0.353 0.363 1.40 Ed/MPa 0.031 0.032 0.032 0.033 1.24 Gd/MPa 11.431 11.823 11.875 12.215 2.20 UCS/MPa 97.13 121.75 122.41 137.42 6.94 片麻岩纵节理 55 ρ/(g·cm−3) 2.625 2.652 2.649 2.684 0.53 SRH 60.67 66.19 66.00 71.33 3.68 vp/(km·s−1) 2.652 3.637 3.688 4.395 12.91 μd 0.308 0.329 0.330 0.333 1.15 Ed/MPa 0.030 0.033 0.033 0.035 5.86 Gd/MPa 11.221 12.148 12.193 13.121 5.13 UCS/MPa 119.66 137.65 137.95 157.74 5.46 注：ρ为密度；SRH为施密特锤回弹高度；vP为纵波波速；μd为动泊松比；Ed为动弹性模量；Gd为动剪切模量；UCS为岩石单轴抗压强度，下同 
下载: 导出CSV
表 2 激活函数种类
Table 2. Types of activation functions
序号 函数名称 表达式 图像 1 Sigmoid $ {f}{}{(}{x}{)=}\dfrac{{1}}{{1}{+}{{\mathrm{exp}}}{(-}{x}{)}} $ 
2 Tanh $ {f}{}{(}{x}{)}{=}\dfrac{{1-{\mathrm{exp}}}{(}{-2x}{)}}{{1+{\mathrm{exp}}}{(}{-2x}{)}} $ 
3 ReLU $ f(x)={\mathrm{max}}(0,x) $ 
4 Softmax $ f(x){=}\dfrac{{\mathrm{exp}}(x_{k})}{\displaystyle\sum_{i=1}^{n}{\mathrm{exp}}(x_{i})} $ 
下载: 导出CSV
表 3 神经元数量与不同激活函数在训练集和测试集上的RMSE值比较
Table 3. Comparison of RMSE values between the number of neurons and different activation functions on the training and test sets
RMSE/MPa 隐藏层神经元数量 函数名称 Sigmoid ReLU Tanh Softmax 训练集 测试集 训练集 测试集 训练集 测试集 训练集 测试集 2 0.0580 0.0591 0.0617 0.0626 0.0564 0.0604 0.0562 0.0572 4 0.0576 0.0600 0.0599 0.0610 0.0553 0.0600 0.0562 0.0570 8 0.0570 0.0610 0.0577 0.0603 0.0550 0.0582 0.0560 0.0577 16 0.0570 0.0620 0.0570 0.0621 0.0554 0.0582 0.0560 0.0577 32 0.0576 0.0653 0.0576 0.0633 0.0554 0.0601 0.0561 0.0579 64 0.0596 0.0707 0.0555 0.0622 0.0596 0.0607 0.0562 0.0577
下载: 导出CSV
表 4 测试集数据分配
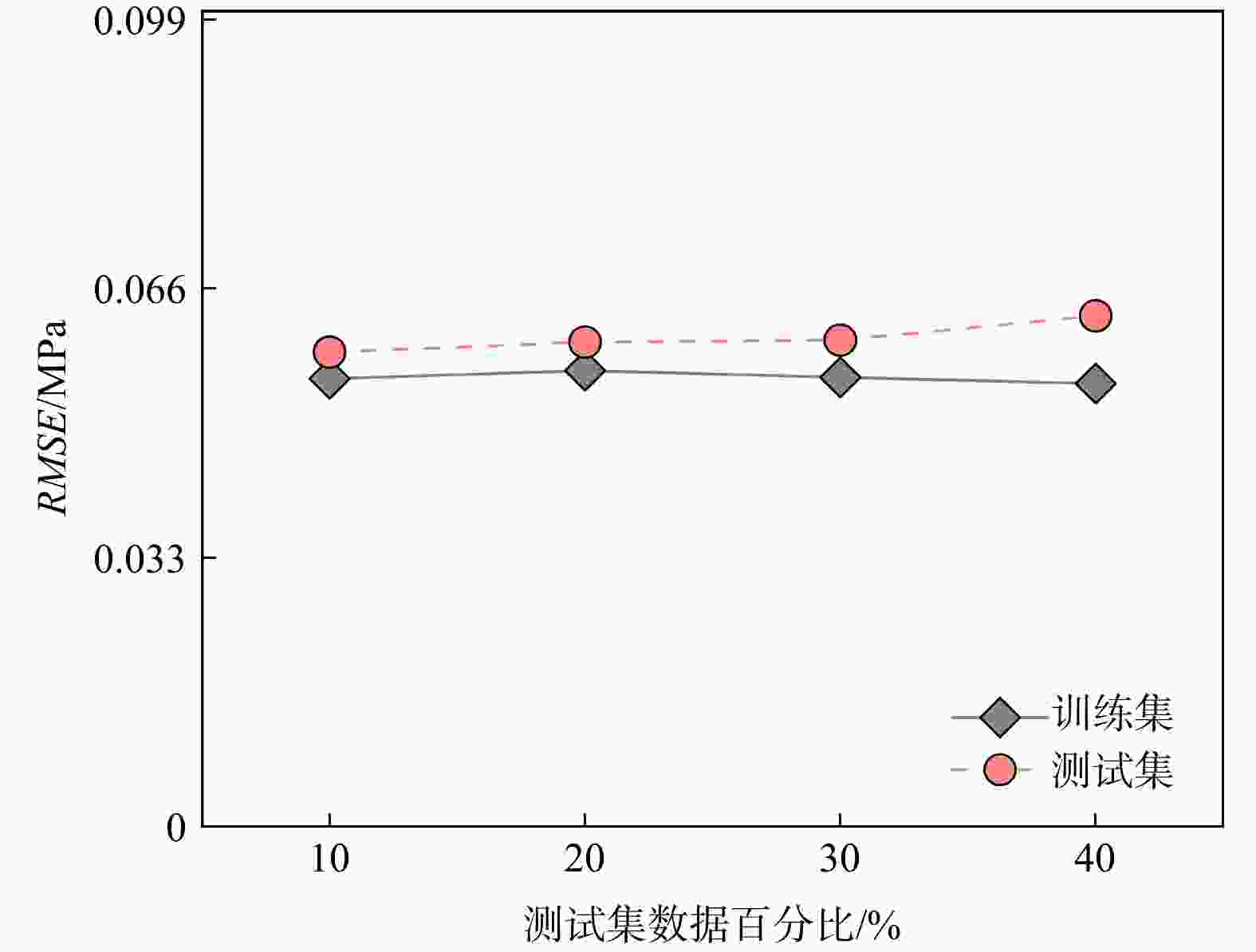
Table 4. Data allocation for the testing set
岩性 数据量 数据量占比/% 测试集数据百分比/% 10 20 30 40 砂岩 56 26.9 6 12 17 22 花岗岩 56 26.9 6 12 17 22 片麻岩横节理 41 19.7 4 8 12 17 片麻岩纵节理 55 26.5 5 10 16 22 合计 208 100 21 42 62 83
下载: 导出CSV
-
[1] 申培武,唐辉明,宁奕冰,等. 基于损伤分区与同一强度理论的岩石本构模型[J]. 地质科技通报,2020,39(5):47-54.SHEN P W,TANG H M,NING Y B,et al. Rock constitutive model based on damage partition and unified strength theory[J]. Bulletin of Geological Science and Technology,2020,39(5):47-54. (in Chinese with English abstract [2] 李志刚,叶宏林,刘伟,等. 干湿循环作用下云母石英片抗压性能劣化规律及机理[J]. 地质科技通报,2023,42(5):36-42.LI Z G,YE H L,LIU W,et al. Law and mechanism of compressive degradation of mica quartz schist under dry wet cycles[J]. Bulletin of Geological Science and Technology,2023,42(5):36-42. (in Chinese with English abstract [3] 杨泽君. 岩石强度回弹法测定的研究[D]. 湖南湘潭:湖南科技大学,2015.YANG Z J. Research on the determination of rock strength by rebound method [D]. Xiangtan,Hunan:Hunan University of Science and Technology,2015. (in Chinese with English abstract [4] MISHRA D A,SRIGYAN M,BASU A,et al. Soft computing methods for estimating the uniaxial compressive strength of intact rock from index tests[J]. International Journal of Rock Mechanics and Mining Science,2015,80:418-424. doi: 10.1016/j.ijrmms.2015.10.012 [5] 曹贵,雷磊. 基于回弹法测试岩石表面强度影响因素分析[J]. 中国建材科技,2014,23(3):16-18. doi: 10.3969/j.issn.1003-8965.2014.03.007CAO G,LEI L. Analysis the strength influence factors of rock surface based on rebound test[J]. China Building Materials Technology,2014,23(3):16-18. (in Chinese with English abstract doi: 10.3969/j.issn.1003-8965.2014.03.007 [6] 王凯笛. 岩石强度的回弹测试研究现状分析[J]. 科学技术创新,2020(30):129-130. doi: 10.3969/j.issn.1673-1328.2020.22.077WANG K D. Analysis of the current status of research on rebound testing of rock strength[J]. Science and Technology Innovation,2020(30):129-130. (in Chinese with English abstract doi: 10.3969/j.issn.1673-1328.2020.22.077 [7] ALIYU M M,SHANG J,MURPHY W,et al. Assessing the uniaxial compressive strength of extremely hard cryptocrystalline flint[J]. International Journal of Rock Mechanics and Mining Sciences,2019,113:310-321. doi: 10.1016/j.ijrmms.2018.12.002 [8] WANG M,WAN W. A new empirical formula for evaluating uniaxial compressive strength using the Schmidt hammer test[J]. International Journal of Rock Mechanics and Mining Sciences,2019,123:94-104. [9] MISHRA D A,BASU A. Estimation of uniaxial compressive strength of rock materials by index tests using regression analysis and fuzzy inference system[J]. Engineering Geology,2013,160:54-68. doi: 10.1016/j.enggeo.2013.04.004 [10] YILMZA I. A new testing method for indirect determination of the unconfined compressive strength of rocks[J]. International Journal of Rock Mechanics and Mining Science,2009,46(8):1349-1357. doi: 10.1016/j.ijrmms.2009.04.009 [11] 刘宗平,王润起,吴小林,等. 施密特锤试验数据处理方法及其在预估岩石可钻性中的应用[J]. 现代地质,1990,4(4):113-125.LIU Z P,WANG R Q,WU X L,et al. Schmidt's hammer test data processing method and its application to the prediction of rock drillability[J]. Modern Geology,1990,4(4):113-125. (in Chinese with English abstract [12] BUYUKSAGIS I S,GOKTAN R M. The effect of Schmidt hammer type on uniaxial compressive strength prediction of rock[J]. International Journal of Rock Mechanics and Mining Science,2007,44(2):299-307. doi: 10.1016/j.ijrmms.2006.07.008 [13] 刘翠,李忠,徐飞亚,等. 考虑微裂纹力学行为的岩石单轴压缩损伤模型[J]. 水文地质工程地质,2024,51(6):104-112.LIU C,LI Z,XU F Y,et al. A compressive damage model for a rock considering the microcrack mechanical behavior[J]. Hydrogeology & Engineering Geology,2024,51(6):104-112. (in Chinese with English abstract [14] KALLU R,ROGHANCHI P. Correlations between direct and indirect strength test methods[J]. International Journal of Mining Science and Technology,2015,25(3):355-360. doi: 10.1016/j.ijmst.2015.03.005 [15] SENGUN N,ALTINDAG R,DEMIRDAG S,et al. P-wave velocity and Schmidt rebound hardness value of rocks under uniaxial compressional loading[J]. International Journal of Rock Mechanics and Mining Sciences,2011,48(4):693-696. doi: 10.1016/j.ijrmms.2011.02.007 [16] POLLAK D,GULAM V,BOSTJAN I. A visual determination method for uniaxial compressive strength estimation based on Croatia carbonate rock materials[J]. Engineering Geology,2017,231:68-80. doi: 10.1016/j.enggeo.2017.09.021 [17] SONMEZ H,TUNUSLUOGLU C. New considerations on the use of block punch index for predicting the uniaxial compressive strength of rock material[J]. International Journal of Rock Mechanics and Mining Science,2008,45(8):1007-1014. doi: 10.1016/j.ijrmms.2007.11.001 [18] LI D,WONG L N Y. Point load test on meta-sedimentary rocks and correlation to UCS and BTS[J]. Rock Mechanics and Rock Engineering,2013,46(4):889-896. doi: 10.1007/s00603-012-0299-x [19] YILMAZ I,YUKSEK,A G. An example of artificial neural network (ANN) application for indirect estimation of rock parameters[J]. Rock Mechanics and Rock Engineering,2007,41(5):781-795. [20] CEVIK A,SEZER E A,CABALAR A F,et al. ,Modelling of the uniaxial compressive strength of some clay-bearing rocks using neural network[J]. Applied Soft Computing,2011,11(2):2587-2594. doi: 10.1016/j.asoc.2010.10.008 [21] YESILOGLU G N,SEZER E. A,GOKCEOGLU C,et al. An application of adaptive neuro fuzzy inference system for estimating the uniaxial compressive strength of certain granitic rocks from their mineral contents[J]. Expert Systems with Applications,2013,40(3):921-928. [22] YAGIZ S,SEZER E A,GOKCEOGLU C. Artificial neural networks and nonlinear regression techniques to assess the influence of slake durability cycles on the prediction of uniaxial compressive strength and modulus of elasticity for carbonate rocks[J]. International Journal for Numerical & Analytical Methods in Geomechanics,2012,36(14):1636-1650. [23] HEIDARI M,MOHSENI H,JALALI S H. Prediction of uniaxial compressive strength of some sedimentary rocks by fuzzy and regression models[J]. Geotechnical & Geological Engineering,2018,36:401-412. [24] XUE X H. A novel model for prediction of uniaxial compressive strength of rocks[J]. Comptes Rendus Mecanique,2022,350(1):159-170. [25] 王睿,孟尧尧,任兆丹,等. 基于声波-回弹联合法的岩石强度快速预测[J]. 铁道工程学报,2018,35(10):27-31. doi: 10.3969/j.issn.1006-2106.2018.10.006WANG R,MENG Y Y,REN Z D,et al. Rapid prediction of rock strength based on combined acoustic wave-rebound method[J]. Journal of Railway Engineering,2018,35(10):27-31. (in Chinese with English abstract doi: 10.3969/j.issn.1006-2106.2018.10.006 [26] 王子娟,刘新荣,傅晏,等. 两种岩石试件的"超声–回弹–密度"综合筛选法研究[J]. 岩石力学与工程学报,2018,37(增刊1):3575-3583.WANG Z J,LIU X R,FU Y,et al. Research on the comprehensive screening method of "ultrasound-rebound-density" for two rock specimens[J]. Journal of Rock Mechanics and Engineering,2018,37(S1):3575-3583. (in Chinese with English abstract [27] ISRM. Suggested methods for determining hardness and abrasiveness of rocks[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1978, 15: 89-97.ISRM. Suggested methods for determining hardness and abrasiveness of rocks[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1978,15:89-97. [28] AYDIN A,BASU A. The Schmidt hammer in rock material characterization[J]. Engineering Geology,2005,81(1):1-14. doi: 10.1016/j.enggeo.2005.06.006 [29] BASU A,AYDIN A. A method for normalization of Schmidt hammer rebound values[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(7):1211-1214. doi: 10.1016/j.ijrmms.2004.05.001 [30] 王让甲. 声波岩石分级和岩石动弹性力学参数的分析研究[M]. 北京:地质出版社,1997.WANG R J. Analytical study on acoustic rock grading and dynamic-elastic mechanical parameters of rocks [M]. Beijing:Geological Press,1997. (in Chinese) [31] 中华人民共和国地质矿产部. 岩石物理力学性质试验规程[S]. 北京:地质出版社,1986.Ministry of Geology and Mineral Resources of the People's Republic of China. Test procedure for physical and mechanical properties of rocks [S]. Beijing:Geological Press,1986. (in Chinese) [32] 吴庆增. 基桩声测与动测技术[M]. 北京:中国电力出版社,2009.WU Q Z. Acoustic and dynamic measurement of foundation piles [M]. Beijing:China Electric Power Press,2009. (in Chinese). [33] LIN P Y,CHEN X Y,JIANG M J,et al. Mapping shear strength and compressibility of soft soils with artificial neural networks[J]. Engineering Geology,2022,300:106585. [34] TIEN T L,ATHANASIA D S,ANNA M,et al. Correlating the unconfined compressive strength of rock with the compressional wave velocity effective porosity and schmidt hammer rebound number using artificial neural networks[J]. Rock Mechanics and Rock Engineering,2022,55:6805-6840. doi: 10.1007/s00603-022-02992-8 -
下载:
点击查看大图
计量
- 文章访问数: 36
- PDF下载量: 4
- 被引次数: 0
