气候变化环境下青藏高原含冰冰碛土斜坡水热力耦合特性与长期稳定性

李奇龙; 周佳庆; 李长冬; 刘洪斌; 王雪萦; 吕豪

doi:10.19509/j.cnki.dzkq.tb20240079

气候变化环境下青藏高原含冰冰碛土斜坡水热力耦合特性与长期稳定性

doi: 10.19509/j.cnki.dzkq.tb20240079

1.
中国地质大学（武汉）工程学院，武汉 430074
2.
武汉大学水资源工程与调度全国重点实验室，武汉 430072

基金项目: 国家自然科学基金项目（42277177）；国家重大自然科学基金川藏铁路重大基础科学问题专项（41941017）

详细信息

作者简介:
李奇龙：E-mail：liqilong@cug.edu.cn

通讯作者:
E-mail：jqzhou@whu.edu.cn

中图分类号: P642.22
计量
- 文章访问数: 478
- PDF下载量: 81
- 被引次数: 0
出版历程
- 收稿日期: 2024-03-05
- 录用日期: 2024-06-07
- 修回日期: 2024-06-06
- 网络出版日期: 2025-02-18

Coupling characteristics and stability evolution of ice-rich moraine soil slopes on the Tibetan Plateau under climate change

1.
Faculty of Engineering, China University of Geosciences (Wuhan), Wuhan 430074, China
2.
State Key Laboratory of Water Resources Engineering and Management, Wuhan University, Wuhan 430072, China

More Information

Author Bio:
E-mail：liqilong@cug.edu.cn

Corresponding author: E-mail：jqzhou@whu.edu.cn

摘要

摘要:
全球气候变暖形势严峻，温度的升高将直接导致广泛分布于青藏高原的各类含冰堆积体与冻结堆积体出现冻结区退化、热融沉降、失稳破坏等一系列工程地质问题。随着青藏地区人类生产实践与工程活动的日益频繁，这些工程地质问题将严重威胁着该地区的人民生命财产安全和重大工程建设进程。本研究建立了考虑冰水相变作用的岩土体渗流-传热-变形耦合数值模型，并通过与已有试验研究以及数值模拟研究的结果进行对比，充分验证了所搭建耦合模拟方法的有效性。基于所搭建的耦合模拟方法，聚焦帕隆藏布流域广泛分布的含冰冰碛土斜坡，结合历史气象数据和气候预测数据（SSP1-2.6与SSP5-8.5两种情景下），开展了自2020-2100年，时长80 a的斜坡多场耦合模拟与长期稳定性计算研究。结果表明，坡体内部各深度土体在长期变暖进程中均呈现不同程度的升温，并进一步导致坡体内部冻结区出现不可逆转的退化，从而导致相应的不可逆转的热融沉降与稳定性下降现象。冻结区的退化与其相应导致的不良工程地质现象受未来不同气候演化模式影响巨大。在SSP5-8.5情景下，持续升温至2080年前后，年均大气温度共抬升了3.84 ℃，坡体内部开始出现冻结区不可逆的退化与随之出现的不可逆沉降现象。在2080年坡体表层出现冻结区永久退化之后，坡体的热融沉降进程与稳定性的下降过程开始出现显著的加速现象，直至2100年，坡体热融沉降可达0.06 m，坡体稳定性较2020年下降了6.3%，这一非线性演化特征深刻反映了含冰土体这一特殊岩土材料在温度升高作用下由量变向质变转变的演化过程。而在SSP1-2.6情景下，冰碛土斜坡并未出现显著的冻结区退化与稳定性劣化的现象。本文构建的嵌入气候模型、考虑了冰水相变的岩土体温度-渗流-应力多场耦合模拟平台，量化评估了不同未来气候情景下坡体退化程度与失稳风险，揭示了气候驱动下含冰冰碛土斜坡水热力多场响应机制，阐明了斜坡长期稳定性演化规律，其成果为高寒高海拔地区地质灾害气候响应和区域地质风险评估奠定了重要理论基础。
- 气候变化 /
- 青藏高原 /
- 含冰冰碛土 /
- 水热力耦合 /
- 斜坡稳定性
Abstract: Objective
The climate warming is severe on a global scale, and the increase in temperature directly leads to a series of engineering geological problems, such as the degradation of frozen regions, thermal thawing-induced subsidence, and the failure of various types of ice-rich and frozen geological structures widely distributed in the Qinghai–Tibetan Plateau. With the increasing frequency of human production practices and engineering construction in the Qinghai–Tibet region, these problems seriously threaten the safety of people's lives and property as well as the construction process of major projects in the region.
Methods
A coupled numerical model of seepage, heat transfer, and deformation considering the water–ice phase transition was established in this study, and its efficiency and accuracy were validated by comparisons with previous experimental and simulated studies. Focusing on the widely distributed moraine slopes containing ice in the Parlung Tsangpo Basin, combined with historical meteorological data and climate prediction data (under the scenarios of SSP1-2.6 and SSP5-8.5), the multi field simulation and long-term stability calculation of slopes were carried out for 80 years from 2020 to 2100.
Results
The results revealed that the soil at different depths inside the slope body was warmed to different degrees under the effect of long-term warming process, which further leads to irreversible degradation of the frozen area inside the slope, resulting in irreversible melt-induced settlement and stability degradation. The degradation of frozen area and accompanying unfavorable geological problems are strongly affected by climate evolution patterns. As the temperature continues to rise until around 2080, the mean annual atmospheric temperature increased by 3.84℃ under SSP5-8.5, and irreversible degradation of the frozen zone and the consequent irreversible subsidence began to occur inside the slope. After the permanent degradation of the frozen zone in the surface layer of the slope in 2080, there was a significant acceleration of thawing-induced subsidence increases and stability decreases. Until 2100, thawing-induced subsidence of the slope could reach 0.06 m, and the stability of the slope decreased by 6.3% compared to 2020. This nonlinear evolution feature reveals the evolution mechanism of ice-rich soil from quantitative changes to qualitative changes under the effect of increasing temperature. However, these degradations did not appear under SSP1-2.6.
Conclusion
In this study, a multiphysics coupled simulation platform of temperature-seepage-deformation behaviors that considers the ice–water phase transition was constructed. It quantitatively evaluated the degree of degradation and instability risk of slopes under different future climate scenarios, revealed the multifield response mechanism and long-term stability evolution of ice-rich moraine slopes driven by climate. The results provide an important theoretical foundation for understanding the climate response to geological hazards in high-cold regions and assessing regional geological risk.
- climate change /
- Tibetan Plateau /
- ice-rich moraine soil /
- thermal-hydraulic-mechanics coupling /
- slope stability

HTML全文

随着全球工业化进程的不断推进，全球在过去的几十年经历了严峻的气候变暖^[1-2]。青藏高原作为全球的“第三极”，更是首当其冲地遭受着气候变暖的冲击^[2-6]，据统计，在过去的几十年，青藏高原地区平均气温的升高幅度要远高于全球平均水平^[5-7]。由于青藏高原地区广泛分布有冰川、冻土等对温度极为敏感的地质结构，持续的气候变暖将显著导致该地区各种地质灾害频发。

滑坡作为青藏高原地区最具代表性的地质灾害之一，威胁着青藏地区的人民生命财产安全以及重大工程建设的安全建设运行。由冰川大幅、多次进退堆积形成的冰碛土滑坡则是其中的一类典型灾害^[8]。由于冰碛土形成于冰川运动过程，所以冰碛土堆积物中常常赋存有不同体积、形状、大小的冰体及冻结物^[9-12]。环境温度升高导致内部冻结物的退化进而导致岩土体强度衰减、变形位移，是导致地质灾害发生的重要原因^[13-16]。1988年7月15日西藏波密米堆沟由于强降雨以及气温上升，导致冰碛土斜坡内冻结物升温融化，然后坡体发生失稳破坏并最终形成大型泥石流^[13]。2007年9月4日、2010年7月23日以及2018年7月11日西藏波密天摩沟由于持续高温及强降雨，导致坡体内部埋藏冻结物大规模消融退化，造成特大泥石流堵塞帕隆藏布江，致使川藏公路G318线路垮塌，交通中断^[17]。因此针对含冰冰碛土斜坡出现失稳破坏机制的探究对于相关地区的防灾减灾工作极为重要。

近几十年来，国内外学者聚焦寒区岩土体已开展了大量的工作。1973年，MCROBERTS等^[18]将冻土边坡的失稳类型归纳为3种，即泥石流、滑坡和崩塌。1990年，王绍令^[19]提出冻土的消融易引起边坡的失稳，且该失稳过程大多为渐变的模式。2006 年，靳德武等^[20]基于青藏高原冻土区的变形监测数据，认为温度升高导致的热融是影响滑体变形的关键因素。2012年，SHAN等^[21]基于现场测试和室内试验的结果，给出了边坡在融化过程中的稳定性与含水量和温度等条件的关系。2014年王超^[22]基于哈大高铁路基边坡土体的室内试验结果，提出了冻融循环次数和含水量与土体力学参数的经验公式，据此对边坡的稳定性进行了分析。近年来，随着数值模拟技术的不断进步，越来越多地用于边坡的稳定性评判研究中，2012年KORSHUNOV等^[23]利用Geostudio 2012软件对冻融前后边坡稳定性做了定量分析，并通过改变水力梯度大小发现了渗流作用的增强对于冰体融化和坡体失稳均有显著的影响，李智明^[24]和CUI等^[25]先后依托有限元软件COMSOL Multiphisics，通过定义冻融前后力学性质的差异，对冻融过程中的边坡采用强度折减法进行了稳定性分析。

综上所述，随着气候的年际高低往复，高寒高海拔地区的边坡内部随之相应地发生着不间断的冻融循环，这一过程显著影响着坡体的稳定性，具体表现为秋冬季节稳定性高，春夏季节稳定性差^[26-31]，且失稳破坏往往发生于解冻区或活动层内部^[29]。同时，寒区边坡的失稳与土体含水率、土体结构以及水热边界条件等多个因素直接相关^[31-32]。但是随着气候的持续变暖，以含冰冰碛土斜坡为代表的各类寒区地质结构将发生何种物理力学演变与稳定性劣化过程，以及在不同气候演化情景下，上述物理力学演化过程将存在何种差异，还是亟待回答的难题。为此，本研究将聚焦于帕隆藏布江流域典型含冰冰碛土斜坡模型，采用有限元数值模拟手段，结合长时间尺度的气候预测数据，以揭示持续气候变暖作用下寒区含冰冰碛土斜坡的水热力演化进程与稳定性演化特征，定量评估未来不同气候演化模式下含冰冰碛土斜坡的退化进程与致灾风险。

1. 研究区概况

1.1 水文地质概况

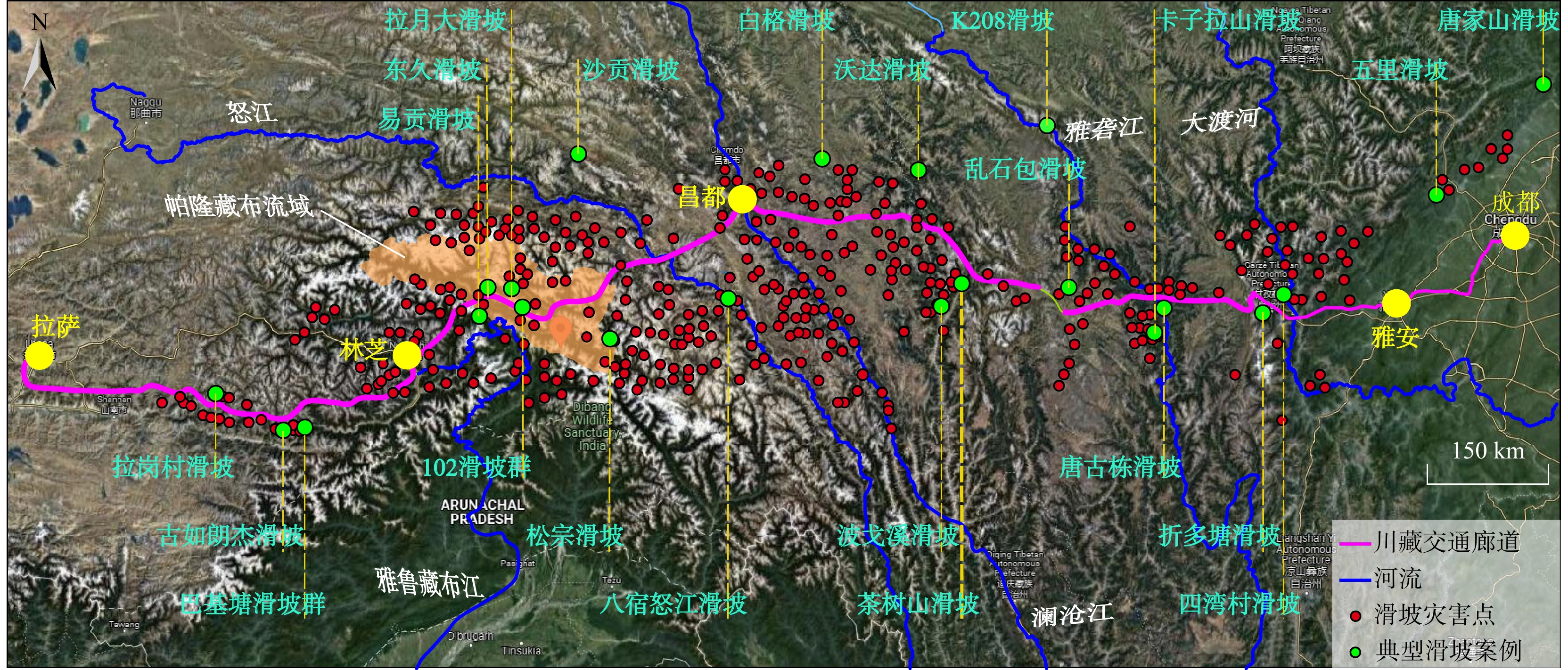
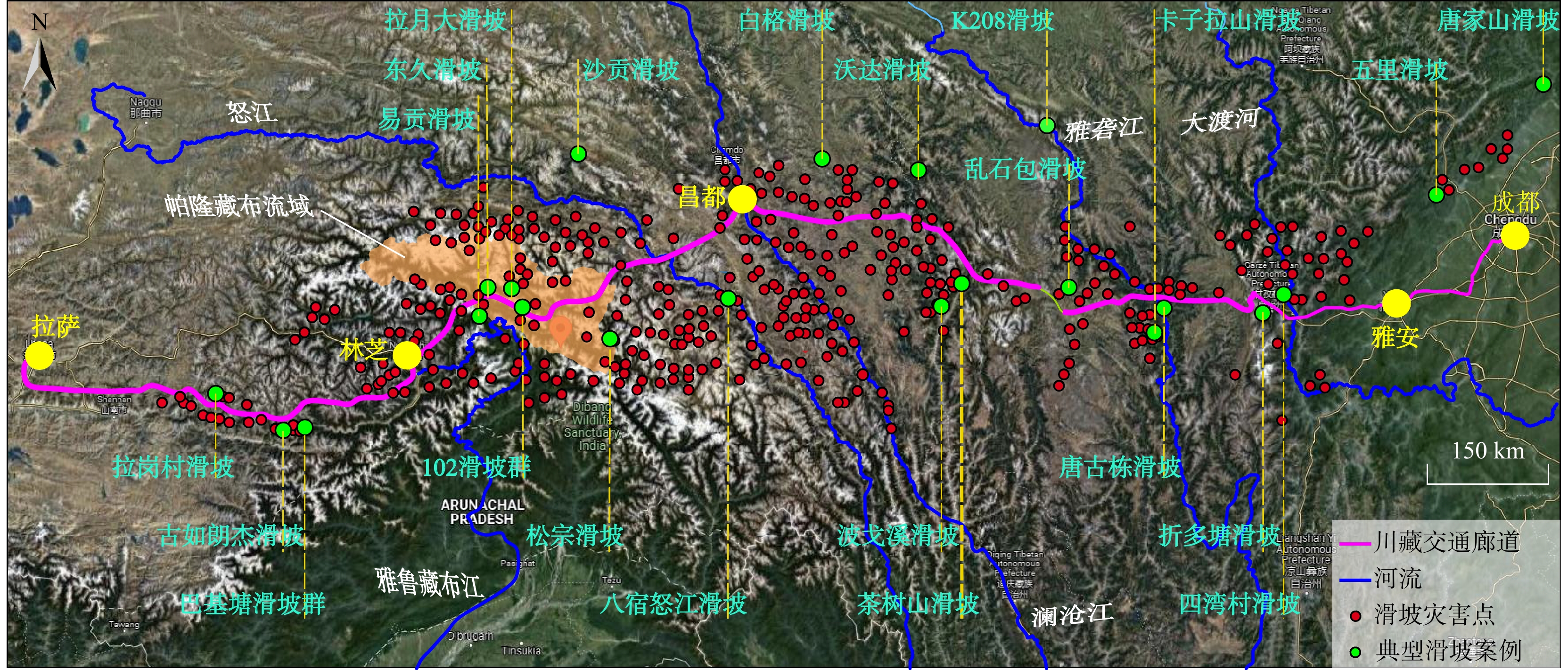
本研究聚焦于青藏高原地区广泛分布的含冰冰碛土斜坡这一特殊地质结构，以帕隆藏布江流域为典型研究区。帕隆藏布江流域位于西藏东南念青唐古拉山和岗日嘎布山之间，是雅鲁藏布江大拐弯北侧最大的支流。帕隆藏布江发源于然乌湖，流经波密县，至通麦与西来的易贡藏布江汇合后向南流入雅鲁藏布江。帕隆藏布江流域由于自身特殊的地质构造条件和水文气象条件以及频繁的冰川活动，该区域含冰冰碛土滑坡、冰雪崩塌、冰川泥石流，冰湖溃决等地质灾害频发。该流域的相关地质灾害具有种类繁多、爆发规模大以及气候敏感性高等特点，因而该流域是川藏交通廊道沿线最为危险的路段之一。如图1所示，在该流域沿线分布着众多纷杂的滑坡灾害点及灾害隐患点。

图 1 研究区灾害点分布概况（滑坡灾害点源自文献[8,33]调研汇编）

Figure 1. Distribution of hazard sites in the study area (Landslide locations are derived from a large number of literature [8,33] research and compilation)

下载: 全尺寸图片幻灯片

在帕隆藏布江流域众多的地质灾害中，含冰冰碛土滑坡是帕隆藏布江流域典型的灾害类型。该类滑坡主要孕育于由冰川运动堆积而成的含冰冰碛土斜坡。由于“小冰期”时期，冰川出现全球性的活跃运动^[34]，冰川运动过程中由于速度快、动能强，通常在其运动的前进方向以及侧向堆积形成大量的松散堆积物，即为冰碛物。这类堆积物通常具有分选差、级配不良的结构特点，加之高寒地区温度极低的气候条件，冰碛物内部常包含有常年不化的埋藏冰体及冻结物。随着冰川退化后移，遗留在冰前及冰侧的冰碛物堆积体即成为现今广泛分布于高寒地区的含冰冰碛土斜坡，这些斜坡通常拥有着陡峭的几何形态和复杂的内部结构。

1.2 气候条件概况

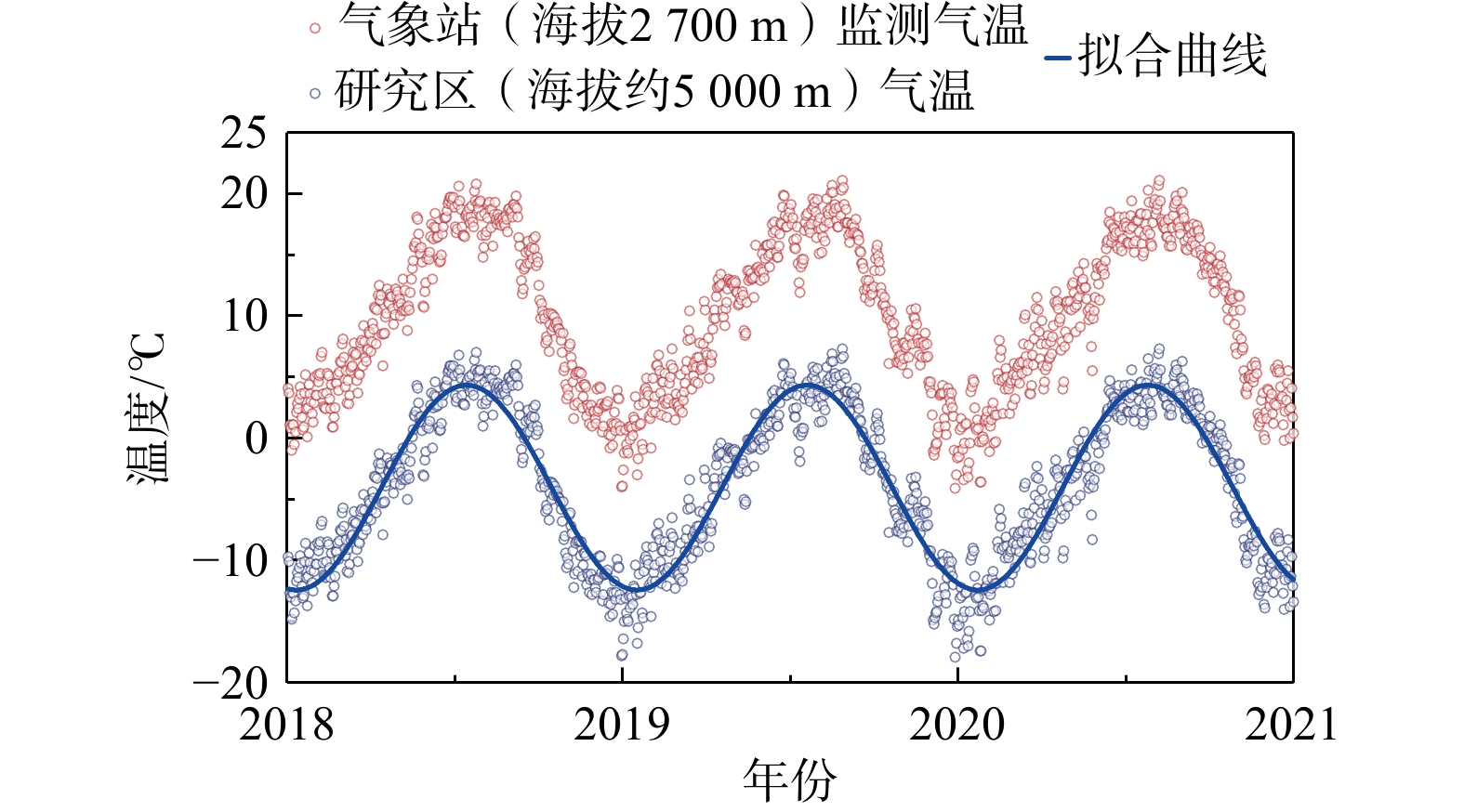
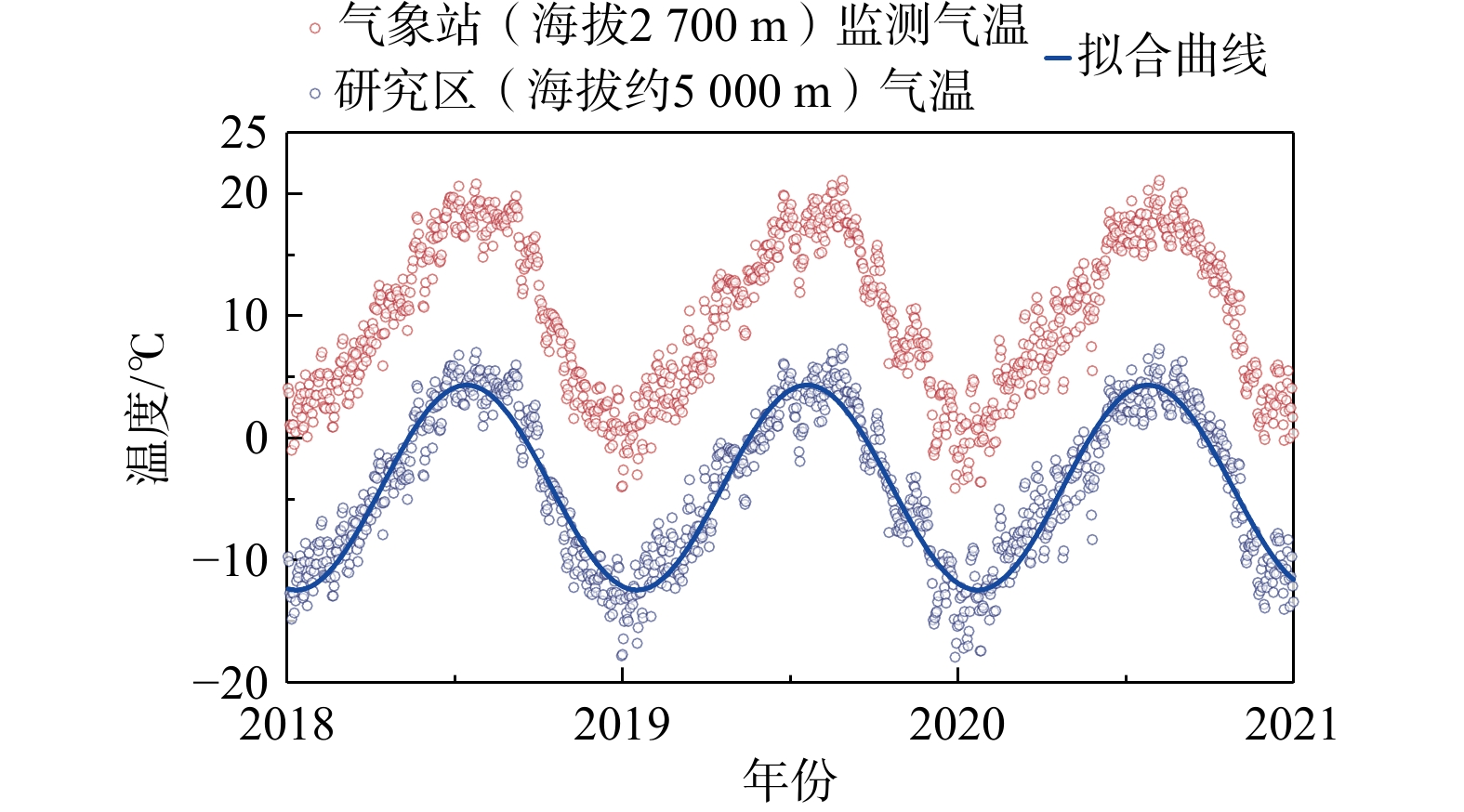
帕隆藏布江流域属于藏东南温带半湿润高原季风气候区，四季分明，冷热明显。由于受热带海洋季风的影响，该流域在夏季高温多雨，具有丰富的热源，是西藏地区平均温度较高的区域。图2统计了帕隆藏布江流域波密气象站（海拔约2700 m）所记录的2018-2020年的日均气温数据，可见其冷暖温差大的气候特点。由于所获取监测数据的气象站位于波密城镇，其海拔相对于冰川、冻土边坡以及含冰冰碛土斜坡所在点位的海拔有显著差距，从而导致气象站的监测气温在数值上不能完全反映研究区的具体温度特征。根据前人关于青藏高原气温与海拔相关性的研究^[35-36]，对获得的监测数据进行修正调整，以更客观合理地对研究区气温特征进行表征描述，调整后的气温数据可见图中蓝色数据点。进一步对调整后的气温数据进行数值拟合，得到式（1），该式可以对研究区的气温波动特征进行概况表征。

图 2 波密地区2018-2020气温波动特征及根据海拔差修正后的研究区气温波动特征

Figure 2. Temperature fluctuation characteristics of Bomê County from 2018 to 2020 and the temperature fluctuation characteristics of the study area corrected according to altitude difference

下载: 全尺寸图片幻灯片

$T_{{\text{air}}}^{\text{0}} = - 5.2 + 8.3\sin (\frac{{2\pi }}{{365}}t + 1.95\pi )，$

(1)

式中： $T_{{\mathrm{air}}}^0$ 为基于波密监测数据经海拔修正后的研究区气温波动表征函数，℃；t为时间，a。

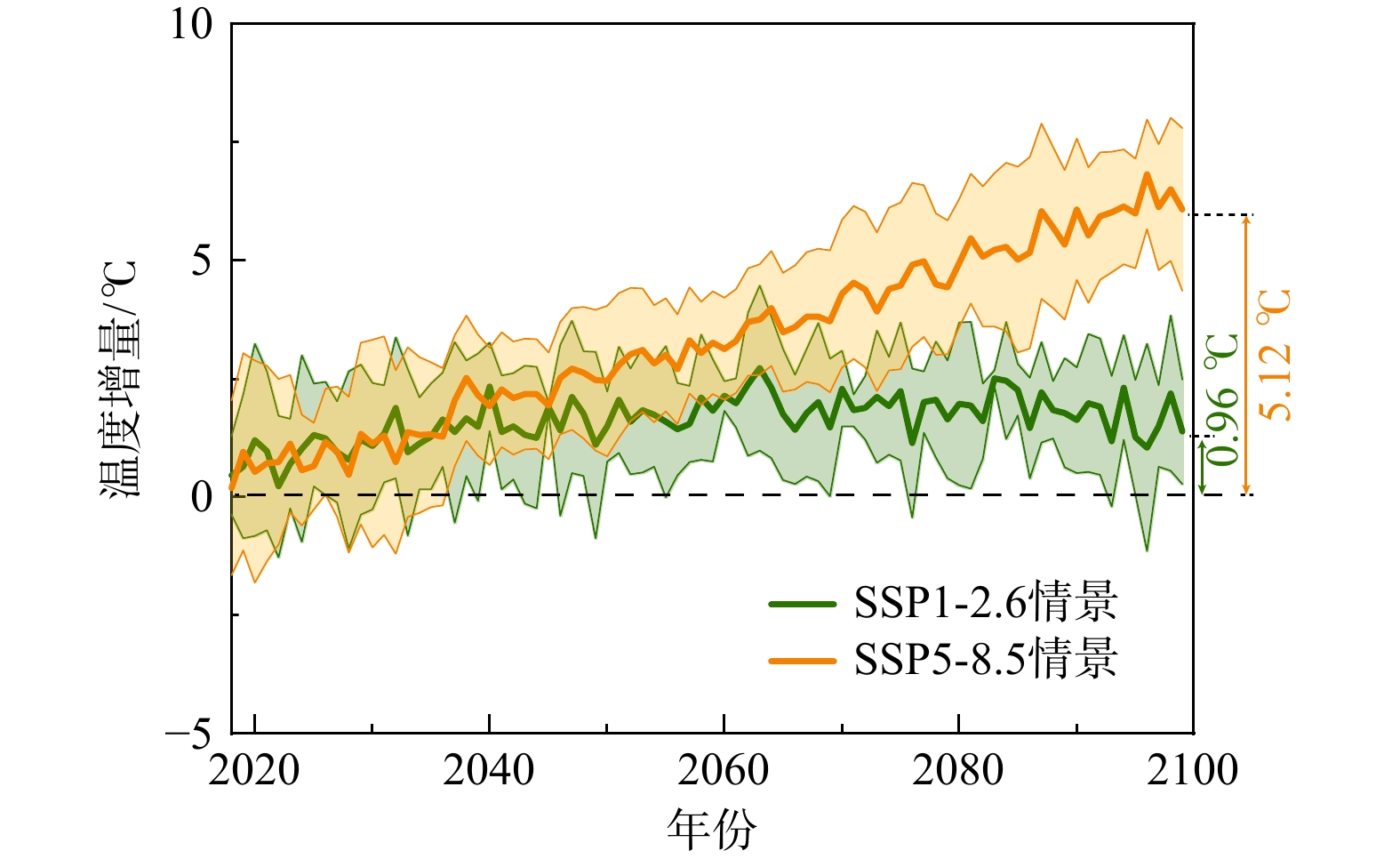
同时，青藏高原作为世界“第三极”，对全球气候变化具有极高的敏感性。第六次国际耦合模式比较计划（CMIP6）汇集了当前最新的气候预测模型，这些模型通过真实完整的物理过程对未来气候进行预测。在预测过程中充分考虑了土地覆盖、土地利用以及社会经济发展等多项因素。模型中不同情景用SSPx-y进行表示，其中x是特定的共享社会经济路径（1～5），y代表2100年长期全球平均辐射强迫水平（2.6～8.5 W/m²）^[37]。图3统计了波密地区在SSP1-2.6（最低辐射强迫水平的可持续发展经济模式）与SSP5-8.5（最高辐射强迫水平的能源密集型经济模式）下的气温增量，在以上2种情景下，大气温度在2020-2100年期间分别上升了约0.96 ℃和5.12 ℃。

图 3 SSP1-2.6与SSP5-8.5情景下波密地区2020-2100气温抬升示意图

Figure 3. Schematic diagram of temperature rise in Bomê County from 2020 to 2100 under SSP1-2.6 and SSP5-8.5 scenarios

下载: 全尺寸图片幻灯片

2. 温度-渗流-应力多场耦合方法

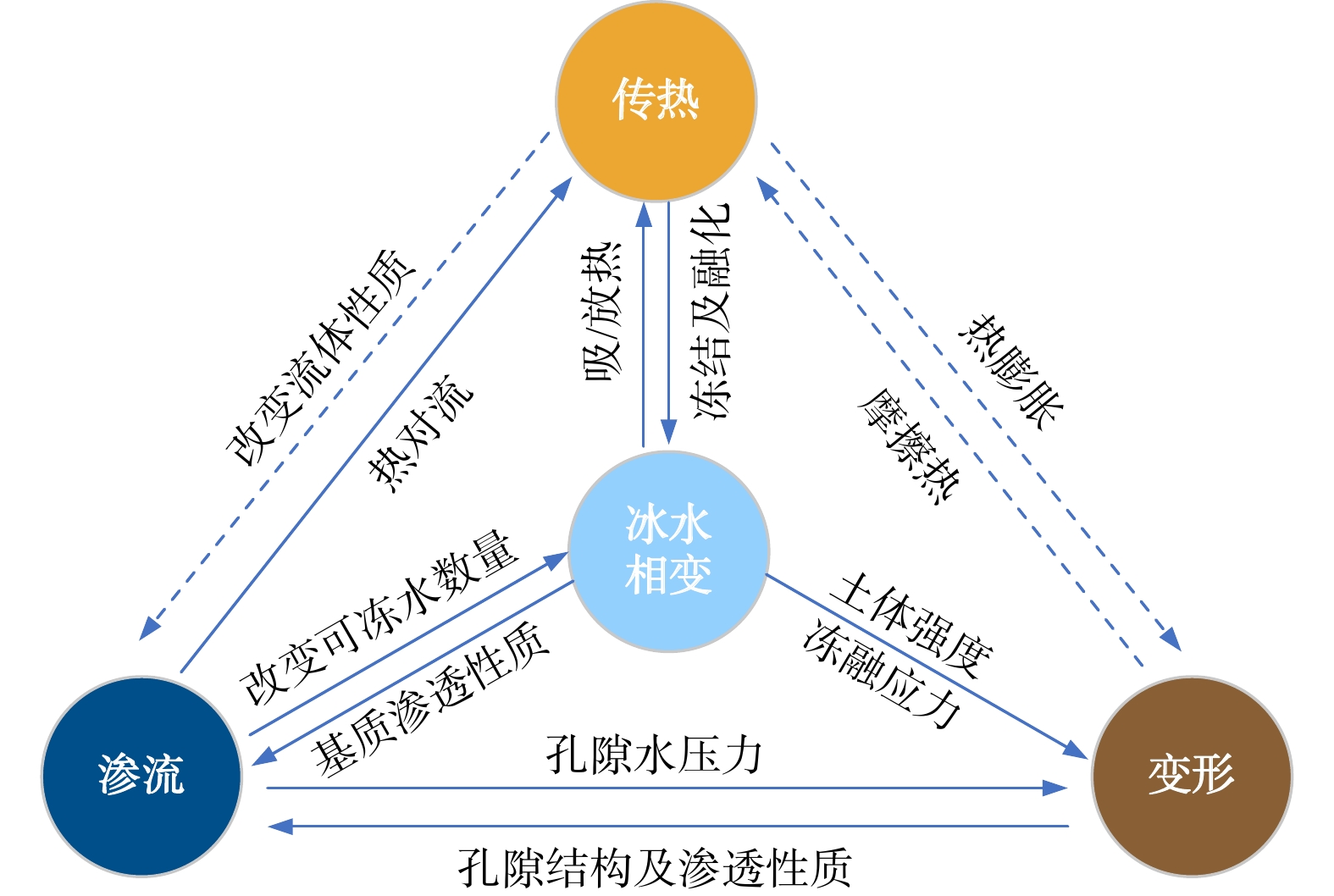
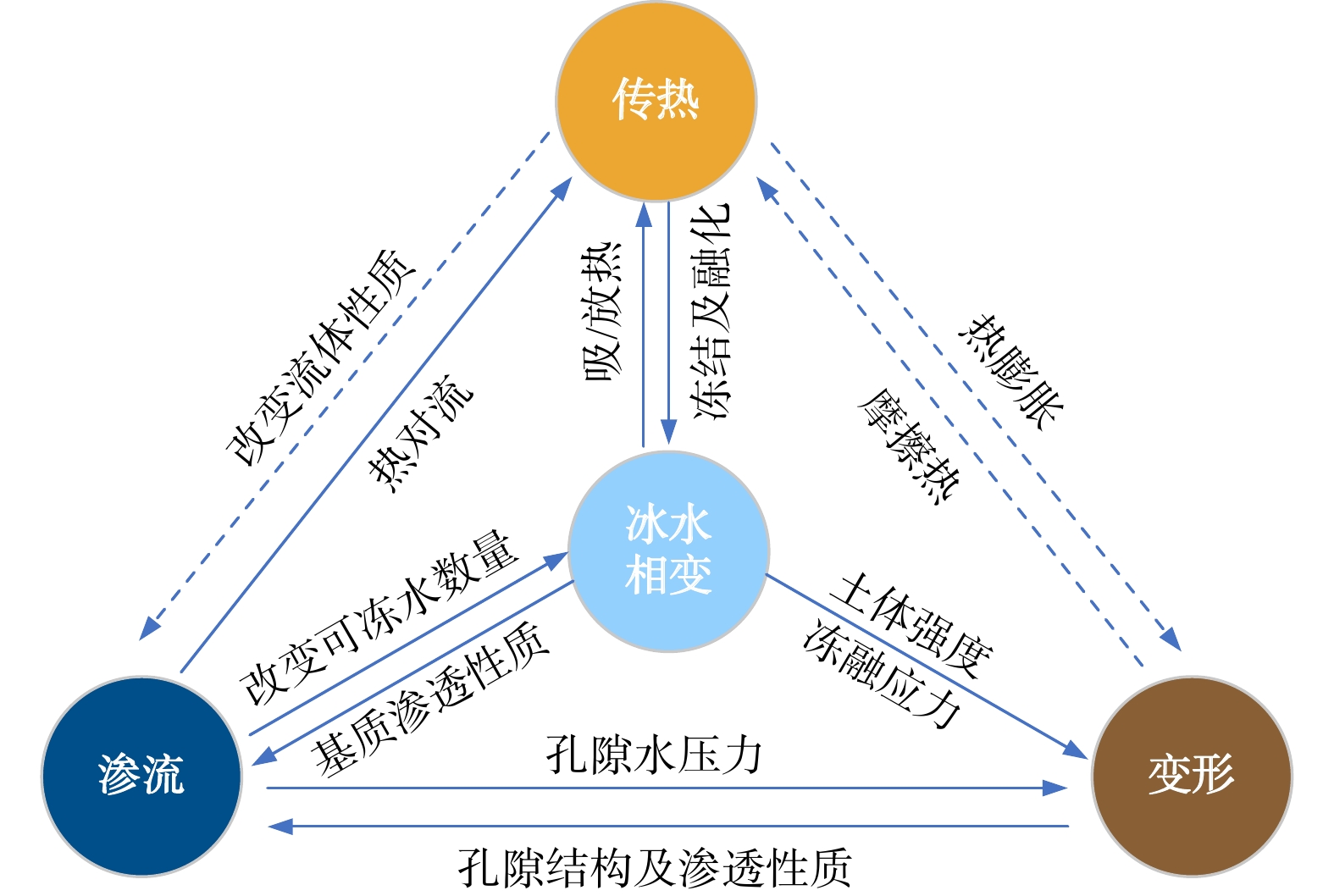
由于富含冰体这一特征，发生于含冰冰碛土斜坡内部的物理力学过程受冰水相变的影响而具有明显的非线性耦合演化特征。具体而言，含冰冰碛土斜坡内部冰水之间的相变过程直接控制着岩土体的流体传输性质、热力学性质以及力学强度性质等，进而影响坡体内部水热力多物理场演化进程（图4）。因而冰水相变过程可以视作含冰冰碛土斜坡内部多物理场耦合作用中的关键因素。本研究着眼于冰水相变过程与渗流-传热-变形物理场之间的作用关系，构建了以冰水相变过程为核心纽带的多物理场耦合数值模拟方法，为探明温度升高环境下寒区含冰冰碛土斜坡的多物理场耦合演化特征奠定了理论基础和技术支持，下面将针对该数值模拟方法中所涉及的相变、渗流、传热、变形理论以及相应的控制方程进行介绍。

图 4 考虑冰水相变作用下传热-渗流-变形耦合示意图（实线表示本模型中所考虑的耦合作用，虚线表示本模型所忽略的耦合作用）

Figure 4. Schematic diagram of heat-seepage-deformation coupling under the consideration of ice-water phase transition (solid line represents the coupling considered in this model, dashed line represents the coupling ignored in this model)

下载: 全尺寸图片幻灯片

2.1 冰水相变过程控制方程

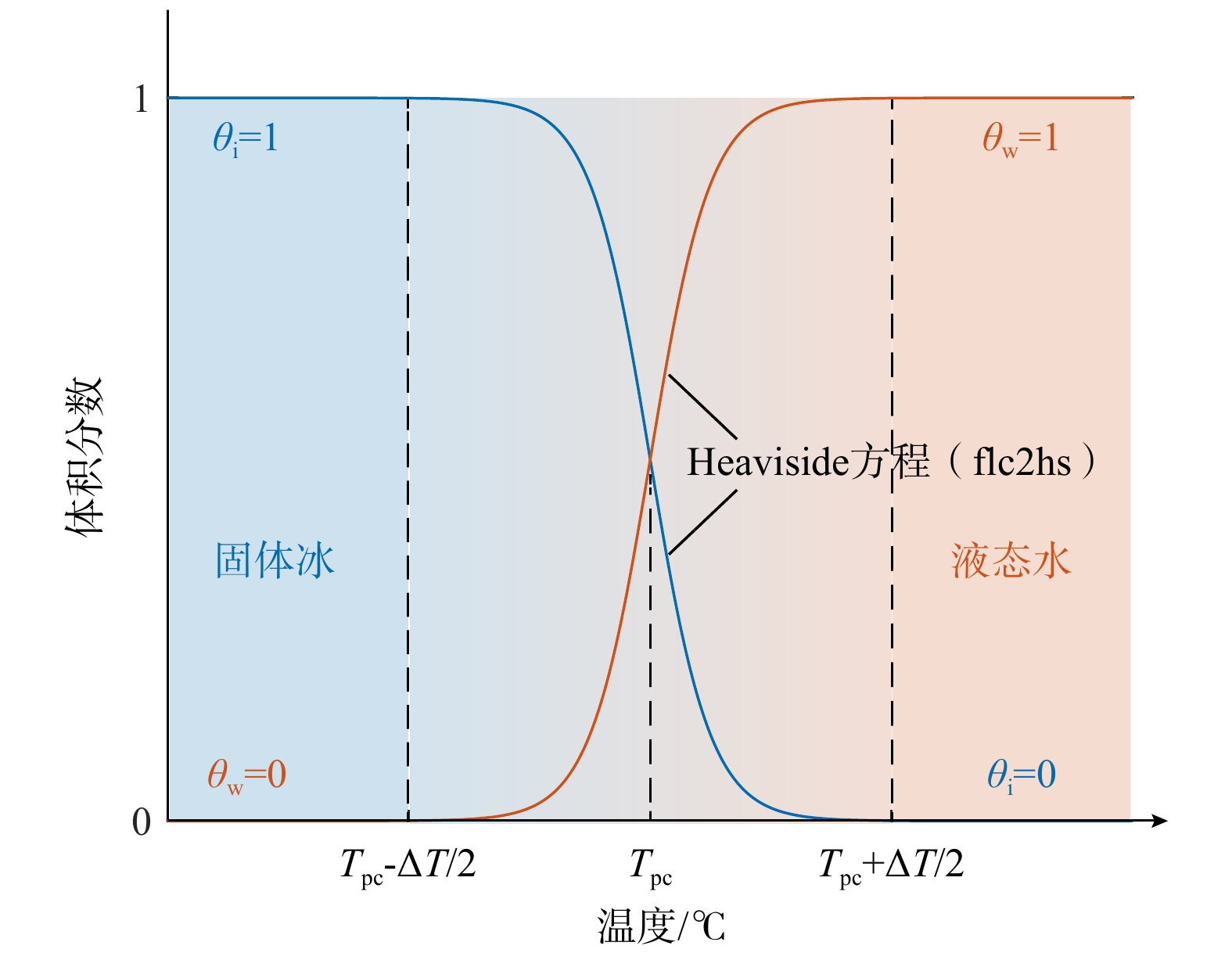
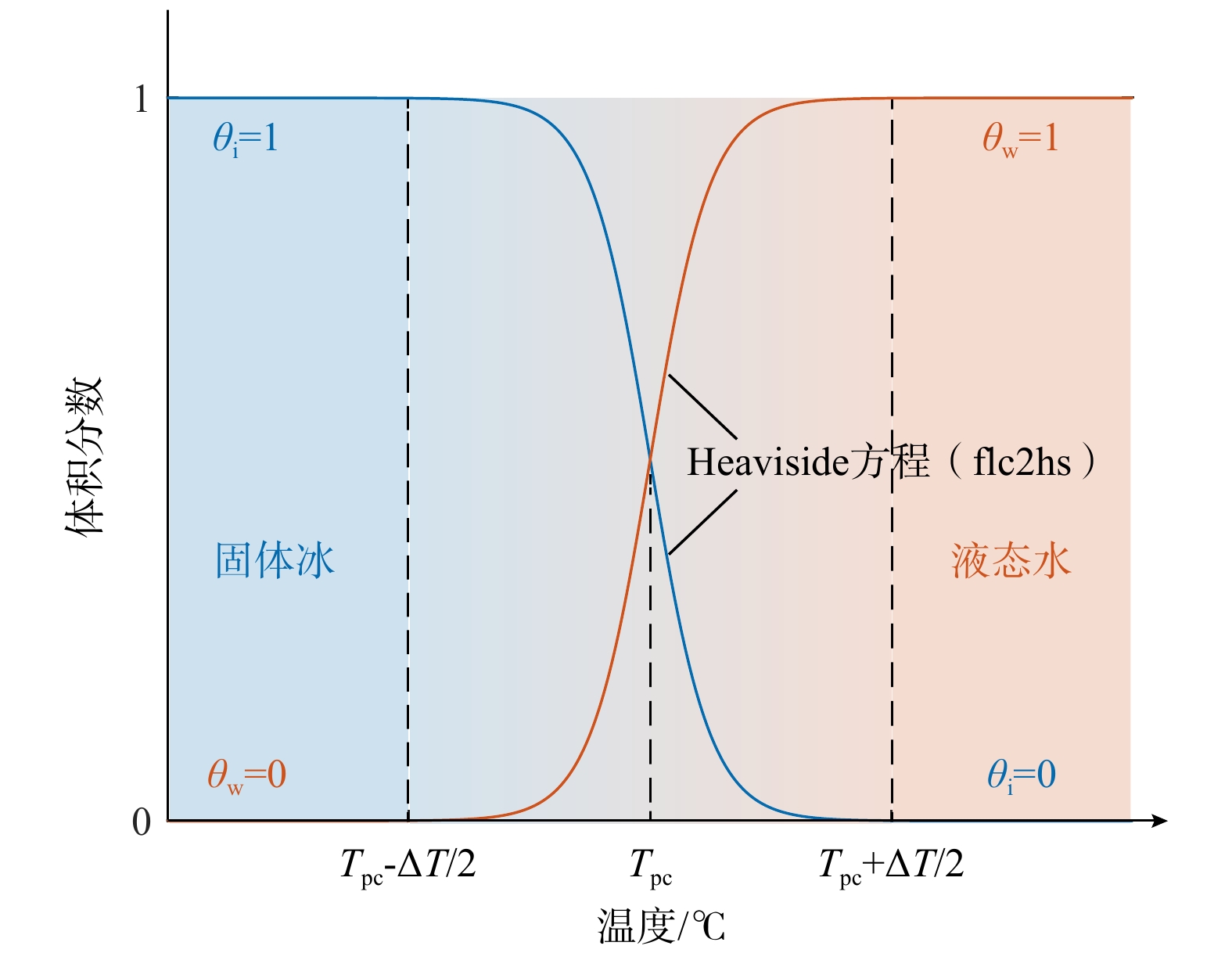
如上文所介绍，含冰冰碛土斜坡内部的冰水相变过程在整个水热力耦合演化进程中起关键纽带的作用，相变过程通过影响土体的各项物理力学性质进而控制着各个物理场的演化进程。因而，如何准确有效地表征冰水相变过程是该模型构建中的关键科学问题。在本研究中，模型采用多物理场耦合模拟软件COMSOL Multiphysics所内置的平滑阶跃函数作为描述冰水相变过程的函数。该阶跃函数以温度为自变量，冰水相对含量为因变量，在相变温度附近设置有一定长度的过渡区间，具体函数图像如图5所示。这样通过过渡函数的设置来表征相变过程是相变模拟研究中常用的方法^[38-39]。在本研究中，相变温度设置为T_pc = 0 ℃，相变过渡区间设置为−1.5～1.5 ℃。

图 5 冰水相变过程示意图

θ_i，θ_w分别为孔隙中冰、水的体积分数；T_pc为相变温度；∆T为地温梯度

Figure 5. Schematic diagram of ice-water phase transition process

下载: 全尺寸图片幻灯片

2.2 考虑冰水相变过程下温度-渗流-应力耦合模型

（1）传热过程控制方程

考虑含冰冰碛土斜坡内存在显著的热对流-热传导作用，根据傅里叶定律，建立考虑相变过程的热对流-热传导方程如式（2）所示，用以描述冻土边坡内部热交换过程。

${(\rho {C_{\mathrm{p}}})_{{\mathrm{eq}}}}\frac{{\partial T}}{{\partial t}} + {\rho _{\text{f}}}{C_{{\mathrm{p}},{\text{f}}}}u \cdot \nabla T + \nabla \cdot ( - {\lambda _{{\mathrm{eff}}}}\nabla T) = 0，$

(2)

式中：T为土体温度；等号左边第2项为热对流项；ρ_f和C_p,f分别表示孔隙内部介质（冰与水）的平均密度和等效热容；u = [n_x, n_y]表示二维渗流速度向量； $\nabla T$ 表示温度梯度。等号左边第3项为热传导项，其中λ_eff表示等效导热系数。

值得一提的是，在本研究中下标f始终代指土体孔隙内部的冰水混合体，模型各处的热力学参数都由土体颗粒骨架（下标s）与孔隙内部相变介质（下标f）以及孔隙内不参与相变的残余水（下标r）共同构成。如式（3）以及式（4）所示，冻土体系的等效恒压热容以及等效导热系数通过各相之间加权平均求得。

${(\rho {C_{\mathrm{p}}})_{{\mathrm{eq}}}} = {\theta _{\mathrm{s}}}{\rho _{\mathrm{s}}}{C_{{\mathrm{p}},{\mathrm{s}}}} + {\varepsilon _0}(1 - {\theta _{\mathrm{r}}}){\rho _{\mathrm{f}}}{C_{{\mathrm{p}},{\mathrm{f}}}} + {\varepsilon _0}{\theta _{\mathrm{r}}}{\rho _{\mathrm{w}}}{C_{{\mathrm{p}},{\mathrm{w}}}}，$

(3)

${\lambda _{{\mathrm{eff}}}} = {\theta _{\mathrm{s}}}{\lambda _{\mathrm{s}}} + {\varepsilon _0}(1 - {\theta _{\mathrm{r}}}){\lambda _{\mathrm{f}}} + {\varepsilon _0}{\theta _{\mathrm{r}}}{\lambda _{\mathrm{f}}}，$

(4)

式中：ρ_f为孔隙内部介质的等效密度，ρ_f=θ_iρ_i+θ_wρ_w；ρ_i，ρ_w分别为孔隙内冰和水的密度；θ_i，θ_w分别为孔隙内冰和水的体积分数；C_p,s ，C_p,f，C_p,w分别表示土体颗粒、孔隙内部混合介质以及水的恒压热容；λ_s，λ_f，λ_w分别表示土体颗粒、孔隙内部混合介质以及水的导热系数；θ_s，θ_r分别代表土体骨架所占体积分数以及土体内部残余未冻水率；ε₀为土体孔隙率。

如式（5）所示，导热系数的计算采用体积平均的方法，其中λ_i和λ_w分别代表冰和水的导热系数。

${\lambda _{\mathrm{f}}} = {\theta _{\mathrm{i}}}{\lambda _{\mathrm{i}}} + {\theta _{\mathrm{w}}}{\lambda _{\mathrm{w}}}。$

(5)

同时，孔隙内部介质又会随温度的变化发生相态的转变（冰与水），这个过程涉及潜热的释放与吸收过程，显著影响着系统的储（放）热作用。如式（6）所示，本研究采用显热容法，通过对水和冰的热容取质量平均继而加上潜热项，从而计算得到孔隙内部介质的等效热容，将复杂的相变问题转换为相对简单易求解的传热问题。

${C_{{\mathrm{p,f}}}} = \frac{1}{\rho }\left( {{\theta _{\text{i}}}{\rho _{\text{i}}}{C_{{\text{p}},{\mathrm{i}}}} + {\theta _{\text{w}}}{\rho _{\text{w}}}{C_{{\text{p}},{\mathrm{w}}}}} \right) + {L_{{\mathrm{ice}} \to {\mathrm{water}}}}\frac{{\partial {\alpha _{\mathrm{m}}}}}{{\partial T}}，$

(6)

${\alpha _{\mathrm{m}}} = \frac{1}{2}\frac{{{\theta _{\text{w}}}{\rho _{\text{w}}} - {\theta _{\text{i}}}{\rho _{\text{i}}}}}{{{\theta _{\text{i}}}{\rho _{\text{i}}} + {\theta _{\text{w}}}{\rho _{\text{w}}}}}，$

(7)

式中：C_p,i，C_p,w分别代表冰和水的恒压热容值；L_ice→water代表相变潜热；α_m为与土体含冰量相关的耦合算子。

（2）渗流过程控制方程

为合理表征含冰冰碛土斜坡内部的渗流过程，本研究采用理查兹方程（8）作为渗流场的控制方程对土体内部饱和-非饱和渗流过程进行描述。

$\rho_{\text{w}}(\frac{C_{\text{m}}}{\rho_{\text{w}}g}+S_{\text{e}}S_{\text{P}})\frac{\partial p}{\partial t}+\nabla\cdot\rho_{\text{w}}[-\frac{k_{\text{eff}}}{\mu}(\nabla p+\rho_{\text{w}}g)]=Q_{\mathrm{m}}，$

(8)

式中：p表示孔隙水压力；ρ_w，μ分别表示水的密度和动态黏度；g为重力加速度；S_p为土体孔隙储水系数；k_eff为土体有效渗透系数；S_e为有效饱和度；C_m为容水度； $\nabla p$ 为压力梯度。

同时，为考虑升温融化或降温冻结过程中伴随的可流动水的增加或减少，在方程（2）右侧设置一个和冰水状态相关的质量源项（Q_m）。Q_m的表达式如方程（9）所示，其中ε_p表示土体有效孔隙度。源项（Q_m）的引入使得冰水相变过程和渗流过程之间的耦合作用能够被有效地表征。

${Q_{\mathrm{m}}} = {\varepsilon _{\mathrm{p}}}({\rho _{\text{i}}} - {\rho _{\text{w}}})\frac{{\partial {\theta _{\text{w}}}}}{{\partial t}}。$

(9)

同时，土体内部的饱和状况将直接影响着土体的宏（微）观渗透特性，在利用理查兹方程描述渗流过程的同时，采用van Genuchten模型以实现对饱和-非饱和工况的表征，引入有效饱和度（S_e）、相对渗透系数（k_r）以及容水度（C_m）来表征不同饱和状态下土体的过流和持水能力。

${S_{\text{e}}} = \left\{ {\begin{array}{*{20}{c}} {{{(1 + {{\left| {\alpha {H_{\text{P}}}} \right|}^n})}^{ - m}}}，&{{H_{\text{P}}} \lt 0} \\ 1,&{{H_{\text{P}}} \gt 0} \end{array}} \right.，$

(10)

${k_{\text{r}}} = {S_{{\mathrm{e}}}}^l{\left[ {1 - {{(1 - {S_{\text{e}}}^{ - m})}^m}} \right]^2}，$

(11)

$m = 1 - \frac{1}{n}，$

(12)

式中：H_p = p/ρ_wg，为确定饱和状态的水头，其中，p为孔隙水压力；ρ_w为水的密度；g为重力加速度；α=1、n=2以及l=0.5均为van Genuchten模型^[40] 的经验参数。容水度（C_m）的数值由有效饱和度以及水头压力共同决定，可由式（13）计算而得。

${C_{\text{m}}} = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{\alpha m}}{{1 - m}}({\theta _{\text{s}}} - {\theta _{\text{r}}}){S_{\text{e}}}^{ - m}{{(1 - {S_{\text{e}}}^{ - m})}^m}}，&{{H_{\text{P}}} \lt 0} \\ 0，&{{H_{\text{P}}} \gt 0} \end{array}} \right. ，$

(13)

同时，式（8）中的S_p为土体孔隙储水系数，由土体的孔隙结构和土体骨架的可压缩性以及流体的可压缩性共同决定，由式（14）及（15）计算而得。

${S_{\text{p}}} = {\varepsilon_{\text{p}}}{\chi_{\text{f}}} + (1 - {\varepsilon_{\text{p}}}){\chi _{\text{p}}}，$

(14)

${\varepsilon}_{\text{p}}={\theta }_{\text{w}}\cdot ({\varepsilon}_{\text{0}}-{\varepsilon}_{\text{r}}）+{\varepsilon}_{\text{r}}+{\varepsilon}_{{\mathrm{vol}}}，$

(15)

式中：χ_f，χ_p分别为流体和多孔介质的可压缩性；ε_p为由土体冻融状态以及土体应力状态共同决定的有效孔隙度；ε₀，ε_r分别为最大孔隙度和孔隙残余含水量；ε_vol为力学过程计算得到的体应变作为水力耦合算子，以表征应力引起的孔隙结构变化对渗流过程的影响，本研究采用水力耦合的经典理论Biot模型定义上述水力耦合作用^[41]。

结合前人对于冻土渗透率演变的研究^[39，42]，本研究定义考虑冻融作用下土体的有效渗透系数k_eff由冻结状态、饱和状态以及土体自身孔隙结构共同决定，其数值由式（16）计算得到。

${k_{{\mathrm{eff}}}} = {k_{{\mathrm{un}}}} \cdot {k_{\mathrm{r}}} \cdot {10^{ - \Omega {\theta _{\mathrm{i}}}}}，$

(16)

式中：k_un = 4×10⁻¹¹ m²为实测于波密现场的未冻结土体渗透率；k_r为van Genuchten模型计算得到的饱和状态相关的相对渗透系数；Ω为冻结阻抗系数。

（3）力学过程控制方程

由于水和冰两种状态的密度有所不同，土体内部的冻结融化通常伴随着土体应力应变状态的改变进而导致相应的土体膨胀和土体沉降。通过线弹性理论对该力学过程进行描述表征，具体方程如下。

平衡方程：

$\nabla \cdot \boldsymbol{\sigma} + {\boldsymbol{F}_{\mathrm{v}}} = 0，$

(17)

式中：σ，F_v分别代表土体内部应力张量以及体积力，σ由初始应力状态、外部应力以及外部应变计算得到：

$\boldsymbol{\sigma} = {{\boldsymbol{\sigma}} _0} + {\sigma _{{\mathrm{ext}}}} + {\boldsymbol{C}}:(\varepsilon - {\varepsilon _{ini}} - {\varepsilon _{{\mathrm{ext}}}})，$

(18)

${\boldsymbol{\varepsilon}} = \frac{1}{2}\left[ {{{(\nabla {\boldsymbol{v}})}^{\rm T}} + \nabla {\boldsymbol{v}}} \right]，$

(19)

式中：σ，ε分别对应土体应力和应变（下标ini表示初始状态）；C = C (E, ν)为表征材料刚度的四阶张量，E和ν分别为杨氏模量和泊松比；v表示位移大小；ε_ext代表冰水相变过程导致的体积应变，由式（20）计算得到；σ_ext代表土体内部渗流场导致的外部应力，本研究参考Biot准则^[40]定义为式（21）：

${\varepsilon _{{\mathrm{ext}}}} = {\varepsilon _0} \cdot (1 - {\theta _{\mathrm{i}}})\left( {\frac{{{\rho _w}}}{{{\rho _{\mathrm{i}}}}} - 1} \right)，$

(20)

${\sigma _{{\mathrm{ext}}}} = - {\alpha _{\mathrm{B}}}p{\boldsymbol{I}}，$

(21)

式中：α_B = 1，为Biot-Willis系数；p为通过水分场计算所得的孔隙水压力；I为单位矩阵。

同时，为探究坡体的稳定性演化过程，本研究采用基于摩尔-库伦准则的强度折减法开展稳定性计算，如式（22）所示。

$\left| \tau \right| + \sigma \tan \varphi - c = 0，$

(22)

式中：φ，c分别为控制土体强度的内摩擦角和黏聚力，而寒区土体在冻融过程自身φ和c的改变是导致斜坡稳定性发生波动的主要原因之一^[16]。本研究采取如式（23）、（24）所示的加权平均算法来描述冻融过程中土体强度参数的变化。

$c = {c_{\mathrm{f}}}{\theta _{\mathrm{f}}} + {c_{{\mathrm{un}}}}{\theta _{{\mathrm{un}}}}，$

(23)

$\varphi = {\varphi _{\mathrm{f}}}{\theta _{\mathrm{f}}} + {\varphi _{{\mathrm{un}}}}{\theta _{{\mathrm{un}}}}，$

(24)

式中：c_f，φ_f分别代表冻结土体的黏聚力和内摩擦角；c_un，φ_un分别代表融化土体的黏聚力和内摩擦角；θ_f，θ_un分别代表冻结水和未冻水的体积分数。

2.3 数值方法有效性验证

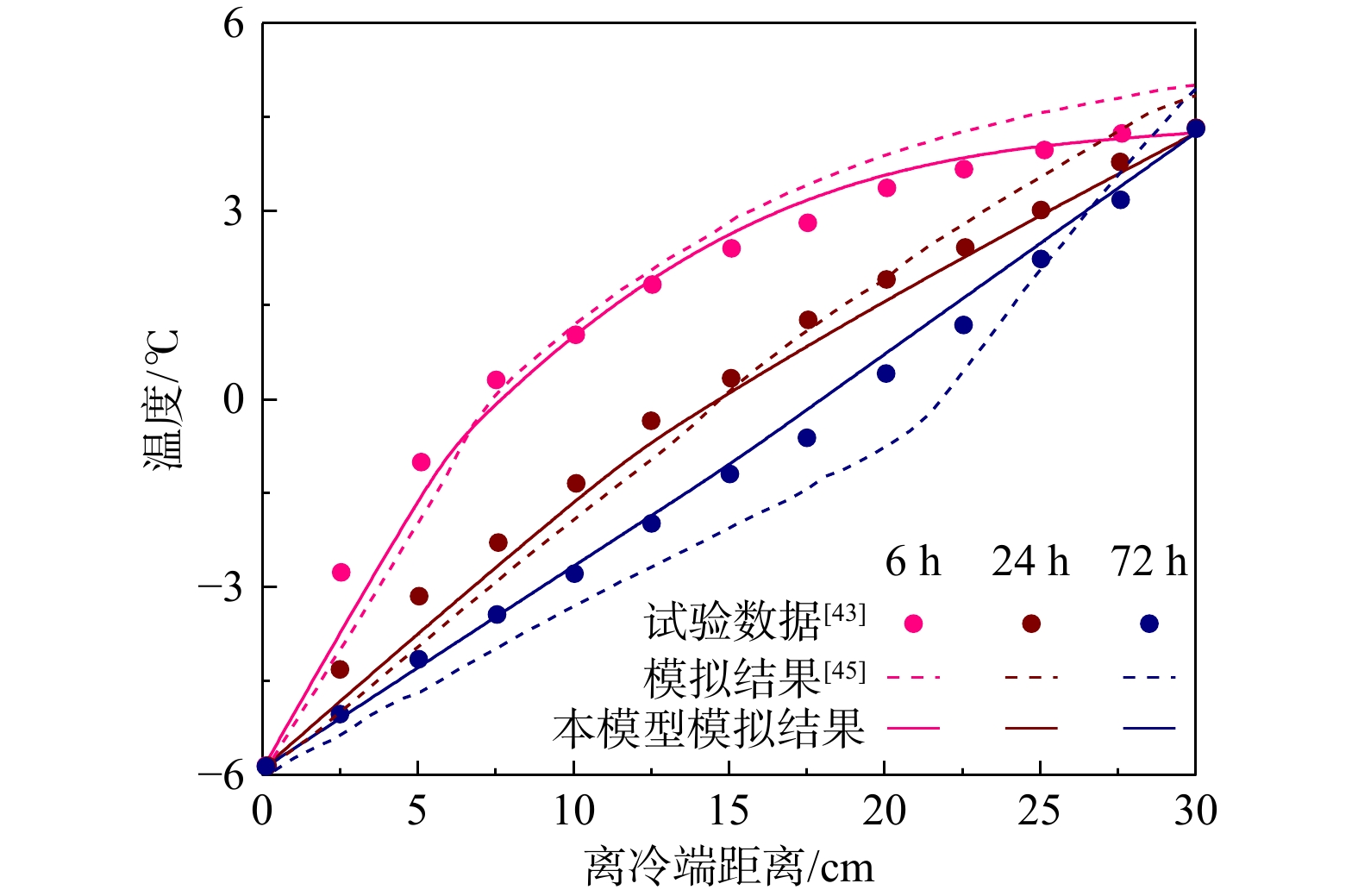
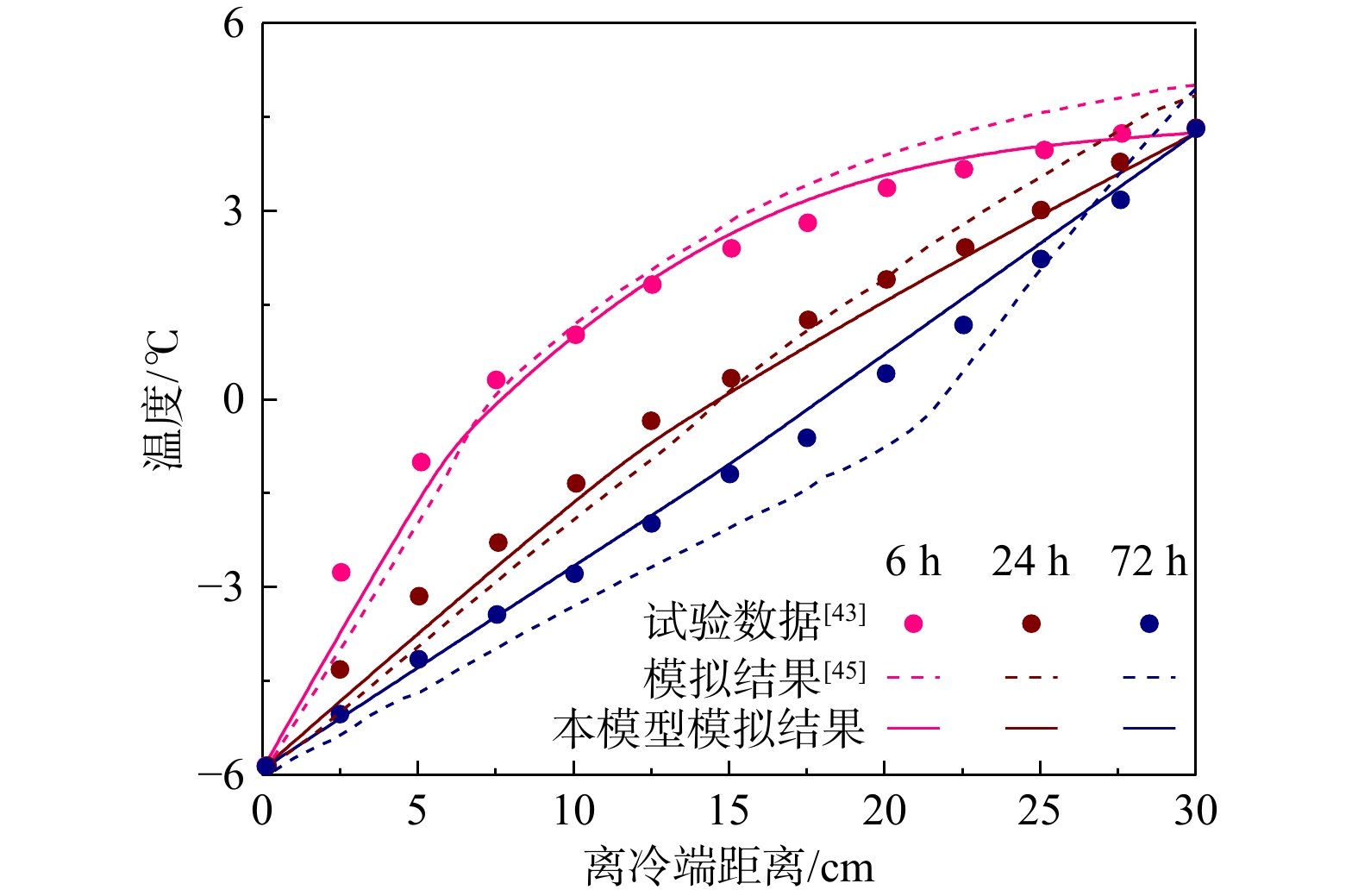
在多孔介质传热相变的众多研究中，JAME^[43]所开展的多孔介质柱体冻结试验被广泛用作验证数值结果准确性与客观性的标准^[44-45]。本研究以JAME^[43]试验研究中的第8组测试结果为标准，对本研究所建立的数值模型进行有效性验证。验证结果如图6所示，通过与试验数据以及前人^[45]模拟研究的对比分析表明，本研究所建立的数值模型能够有效准确地对多孔介质内部水热耦合作用以及相变过程进行客观有效的表征，能够用于模拟含冰冰碛土斜坡内部复杂的水热演化进程。

图 6 数值模型验证对比

数据点为JAME^[43]试验结果；虚线为HUANG等^[45]数值模拟验证结果；实线为本研究所建立数值模型的验证结果

Figure 6. Comparison of numerical model verification

下载: 全尺寸图片幻灯片

3. 含冰冰碛土斜坡水热力耦合特性与稳定性演化规律

3.1 含冰冰碛土斜坡概念模型

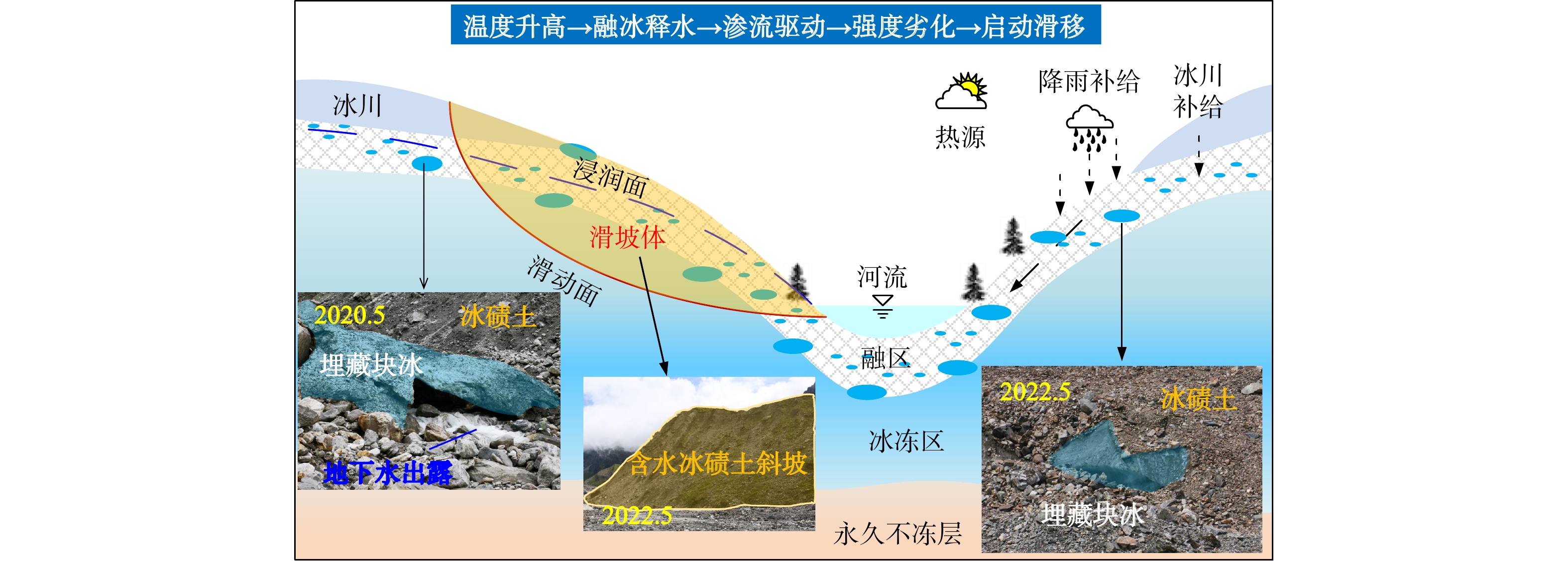
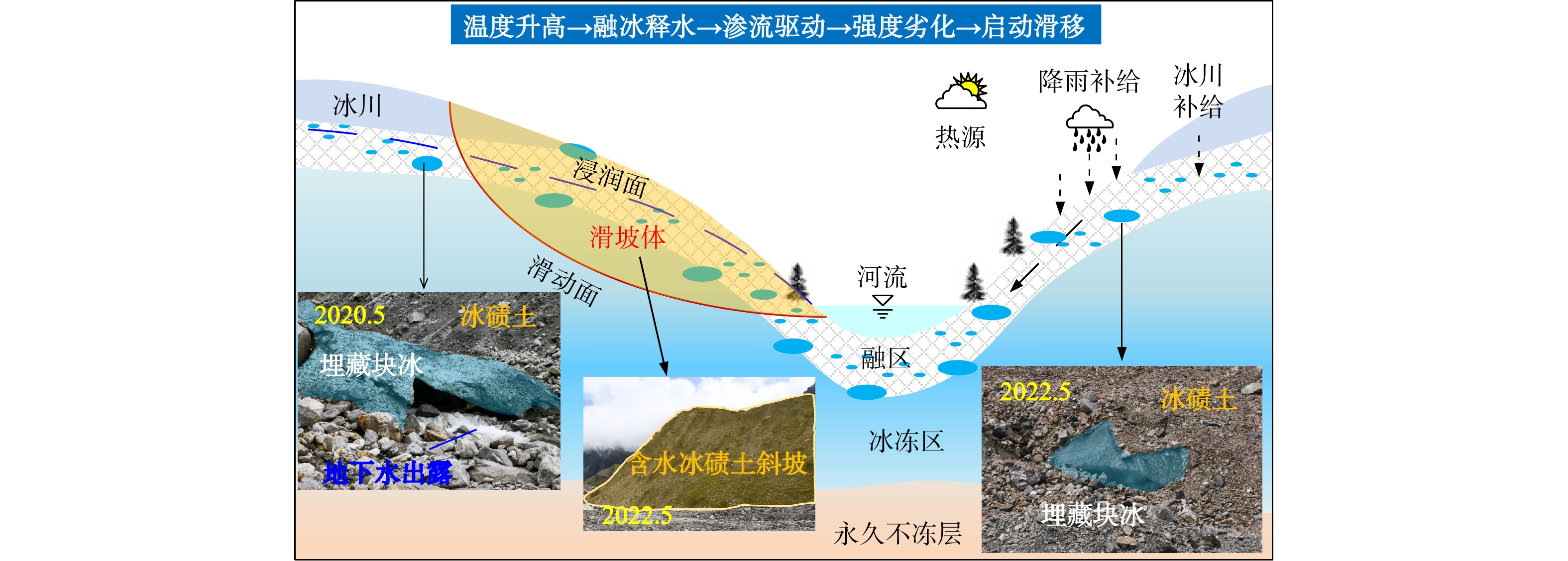
如2.1节所介绍，青藏高原帕隆藏布江流域大量分布的由冰川运动所堆积形成的含冰冰碛斜坡或含冰冰碛坝，这类斜坡内部通常赋存有形式多样的冰体以及冻结物，因而其内部物理力学演化特征极大程度上受温度变化的控制。同时，如图7所示，帕隆藏布江流域的气候条件具有温度波动大、降雨充沛的显著特征，且随全球气候变暖进程，该地区的气候将在未来出现显著升高。温度的升高将导致冻结区的退化、未冻水的增加与土体强度的显著降低，这些宏（微）观的物理力学演变将给含冰冰碛土斜坡的安全稳定带来极大的威胁。为探究含冰冰碛土斜坡在温度升高状况下内部土体物理力学响应过程与整体稳定性的演化特征，本研究建立如图7所示的概念模型。该模型以含冰冰碛土斜坡为主要研究对象，以气候变暖进程中大气温度的升高作为主要热源，旨在探讨气候变暖进程下含冰冰碛土斜坡的水热力耦合特征与稳定性演化过程。

图 7 寒区含冰冰碛土斜坡致灾机理示意图

Figure 7. Conceptual diagram of hazard-causing mechanism of ice-rich moraine landslide in cold regions

下载: 全尺寸图片幻灯片

3.2 含冰冰碛土斜坡边界条件及初始条件

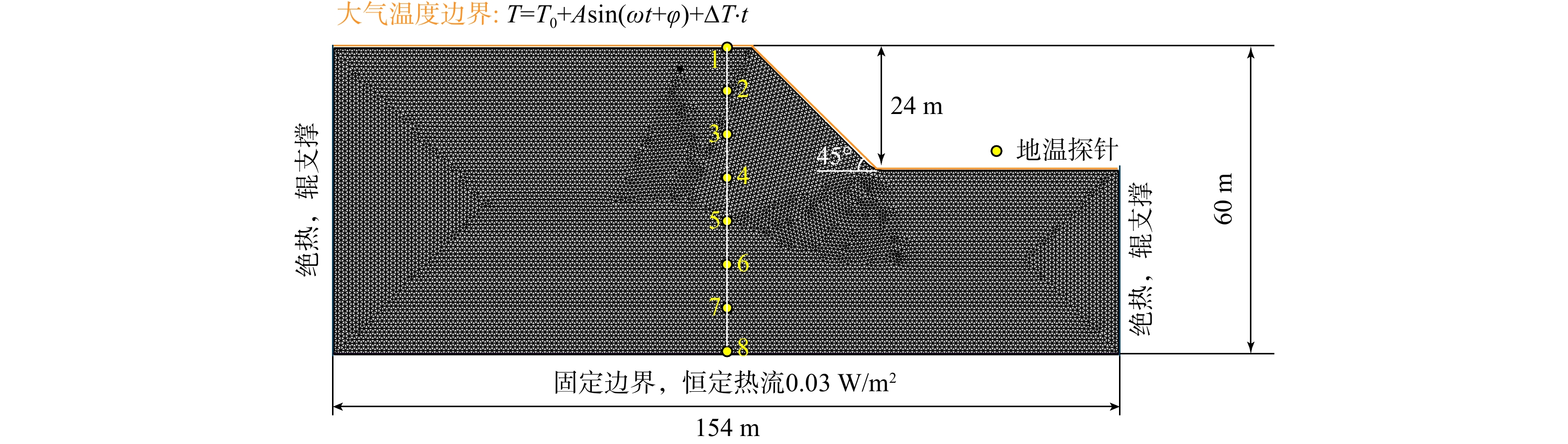
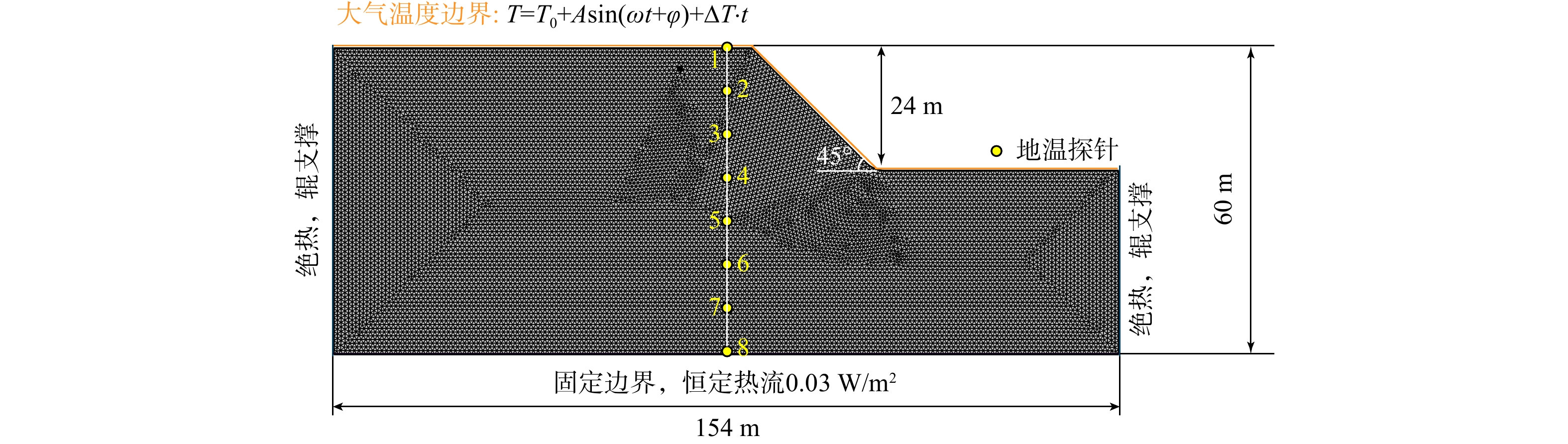
基于对上述含冰冰碛土斜坡的认识，建立典型含冰冰碛土斜坡模型如图8所示。该模型主体为高24 m、坡角45°的土坡，土坡下方由深36 m、长154 m的地下土体组成。该模型上部的表面均为直接与大气接触的地表边界，设置为Neumann边界条件，内向热通量由大气温度T_air配合传热系数h计算而得。根据2.2节所介绍该研究区的历史气候特征以及未来可能出现的气候演变趋势，将历史监测数据与气候预测数据相结合，得到以式（25）进行表征的大气温度T_air，其中升温速率 $\Delta T$ 在SSP1-2.6与SSP5-8.5情景下分别取值为0.012 ℃/a和0.064 ℃/a。模型两侧数值边界设置为绝热的辊支撑边界，底部边界设置为有恒定地热流入的固定边界，恒定地热流设置为0.03 W/m²。由于不考虑降水以及其他形式的水分补给，也不考虑外渗等水分排泄过程，土体内部水分分布仅受冻融作用影响，故所有边界都设置为无流动边界。

图 8 模型几何与边界条件以及网格剖分示意图

注：T为大气温度；T₀为初始年份平均气温；ω为角频率；φ为波动函数初相位；

$\Delta T$ 为升温速率；t为时间；A为温度波动幅值的1/2

Figure 8. Schematic diagram of model geometry and boundary conditions and grid generation

下载: 全尺寸图片幻灯片

$T_{{\text{air}}}^{} = - 5.2 + 8.3\sin (\frac{{2\pi }}{{365}}t + 1.95\pi ){\text{ + }}\Delta T \cdot t。$

(25)

本研究参考前人的研究^[46]，采用循环计算的策略（spin-up strategy），以2018-2020年的气温作为热学边界条件，进行时长为1000 a的模拟计算。直到底部边界温度达到稳定不变，即视为整个坡体达到了这样温度条件下的真实热分布状态，并将这一稳定状态作为后续瞬态计算的初始状态开展研究。这样的计算策略能够在不需要研究区域深层详细地热资料的情况下基于物理过程真实地反演地下土体的温度分布状况，同时有效地避免了将初始状态设置为某一特定均一温度带来的计算误差。

本研究中模型计算涉及的众多物理力学参数均通过现场原位试验、室内试验以及参考前人^[15-16，25]研究获得及选取，如表1所示。

表 1 物理力学参数表

Table 1. Physical and mechanical parameters

参数	数值	描述
ρ_s	2600 kg/m³	土体基质密度
ρ_w	1000 kg/m³	水体密度
ρ_i	918 kg/m³	冰体密度
ε₀	0.15	孔隙率
ε_r	0.05	残余含水率
k_u	4×10⁻¹¹ m²	融土渗透系数
μ	1.793×10⁻³ Pa·s	水体动力黏度
Ω	50	冰体阻抗系数
λ_s	1.07 W/(m·℃)	土体导热系数
λ_w	0.63 W/(m·℃)	水体导热系数
λ_i	2.31 W/(m·℃)	冰体导热系数
C_s	0.93 kJ/(kg·℃)	土体热容
C_w	4.2 kJ/(kg·℃)	水体热容
C_i	2.1 kJ/(kg·℃)	冰体热容
L	334.56 kJ/kg	冰水相变潜热
E_s	100 MPa	土体杨氏模量
$\nu$	0.4	土体泊松比
c_un	60 kPa	融土黏聚力
c_f	200 kPa	冻土黏聚力
φ_un	25 °	融土内摩擦角
φ_f	30 °	冻土内摩擦角

下载: 导出CSV

| 显示表格

3.3 水热力耦合特性

（1）温度场演化特征

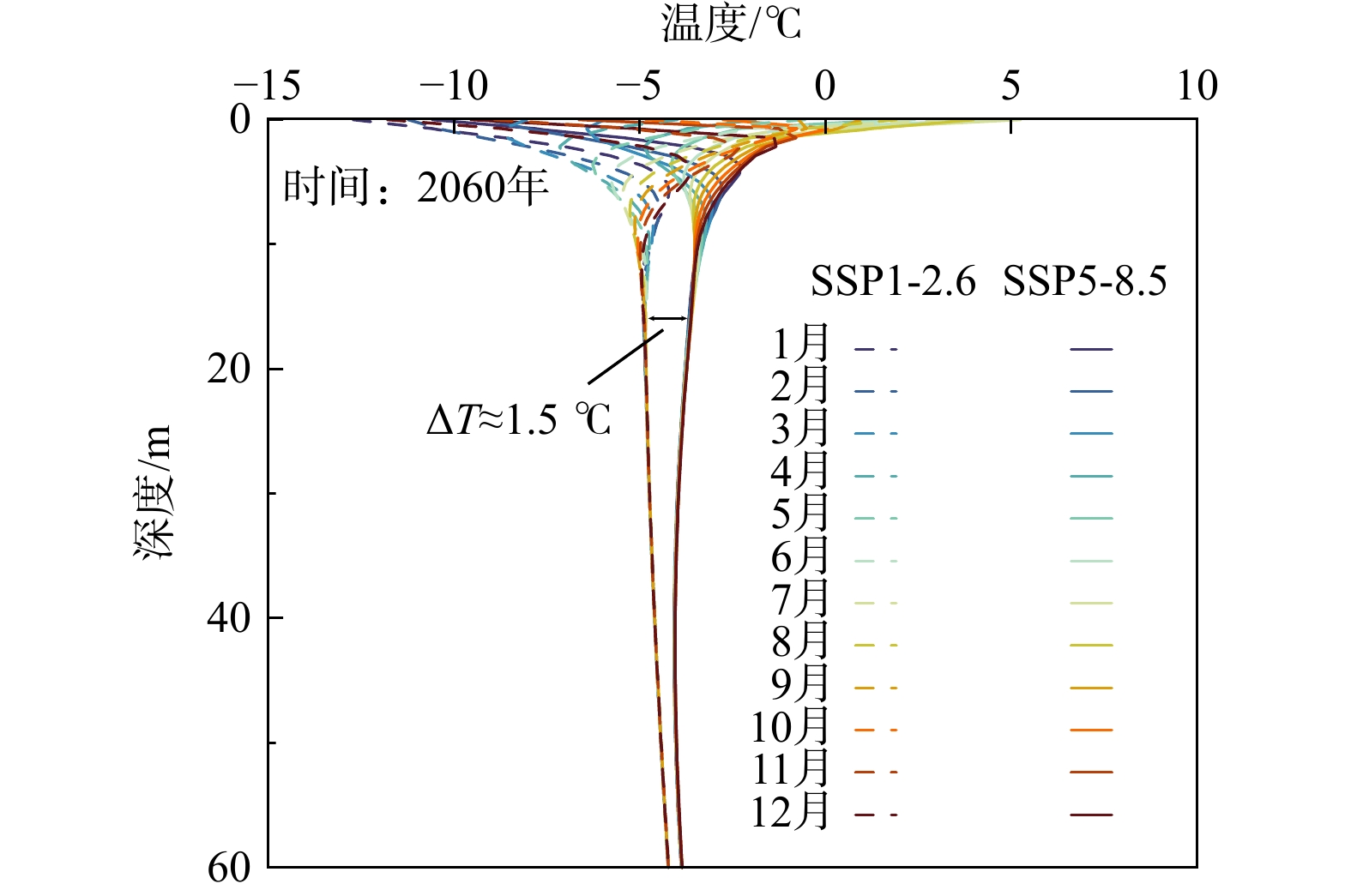
随着季节的更替，大气温度的波动直接影响着坡体内部的温度分布规律。以2059-2060年度的地温分布为例，如图9所示，在气温较高的季节（4-10月），土体呈现浅部温度高、深部温度低的特征；相反，在气温较低的季节（1-3月及11-12月），土体温度规律表现为浅部低而深部相对较高的特征。同时，在一年的气候波动中，大气温度波动对于坡体内部的影响范围有限，以2060年为例，仅20 m深度以内的浅部土体发生季节性的温度波动，即随深度的增加，土体温度的季节性波动特征逐渐微弱。同时，不同气候演变模式下地温演化进程存在显著差异，经历等时长的升温进程，高碳排放情景下（SSP5-8.5）各深度地温升高幅值更大，地温曲线较低碳排放情景下（SSP1-2.6）整体右移，在18 m深度处两种温度升高模式下地温差距（∆T）可达1.5 ℃。

图 9 不同温度升高情景下2060年含冰冰碛土斜坡地温分布特征

Figure 9. Characteristics of ground temperature distribution in ice-rich moraine slopes under different climate warming during 2060

下载: 全尺寸图片幻灯片

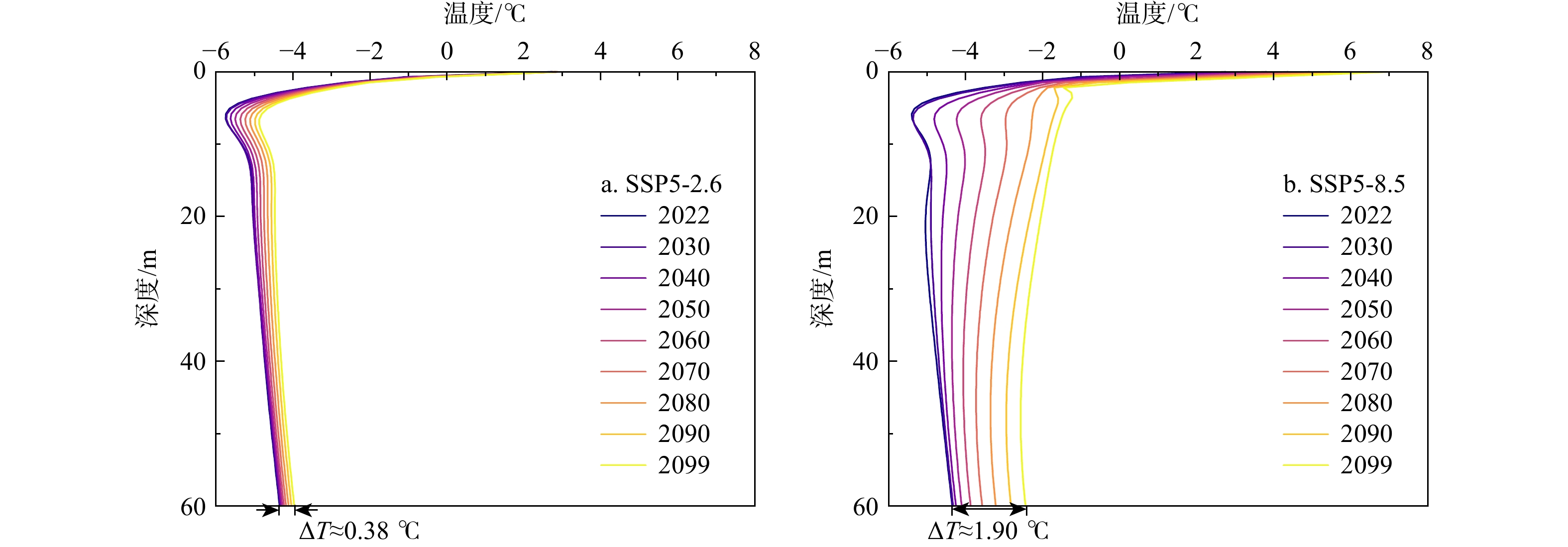
通过每隔10年对夏季中坡体中轴线土体温度分布状态进行统计（图10），可以发现随着时间的推移，气候持续变暖，夏季的地温曲线均出现整体右移。由此可见，尽管在一年内的季节周期内难以察觉大气温度变化对深部土体的影响（图9），但随着更长时间的升温累积，各深度的土体在气候变暖的进程中均出现了不同程度的明显的温度升高。同样地，在长期温升过程中，不同气候情景带来的地温增长差异巨大。以坡体底部（60 m埋深处）为例，土壤温度在SSP1-2.6与SSP5-8.5情景下分别增长了0.38 ℃与1.9 ℃。

图 10 不同温度升高情景下2020-2100年含冰冰碛土斜坡地温分布演化特征

Figure 10. Evolution characteristics of ground temperature distribution in ice-rich moraine slopes under different warming scenarios

下载: 全尺寸图片幻灯片

（2）冻结区演化特征

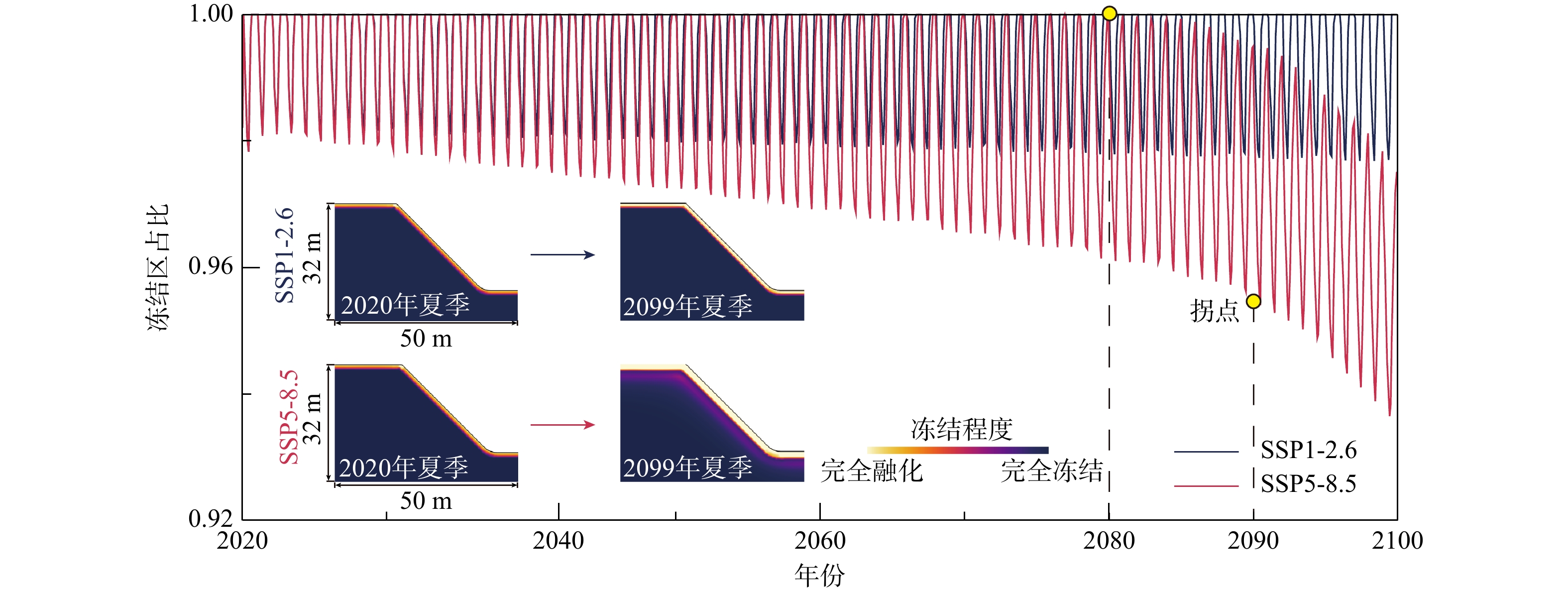
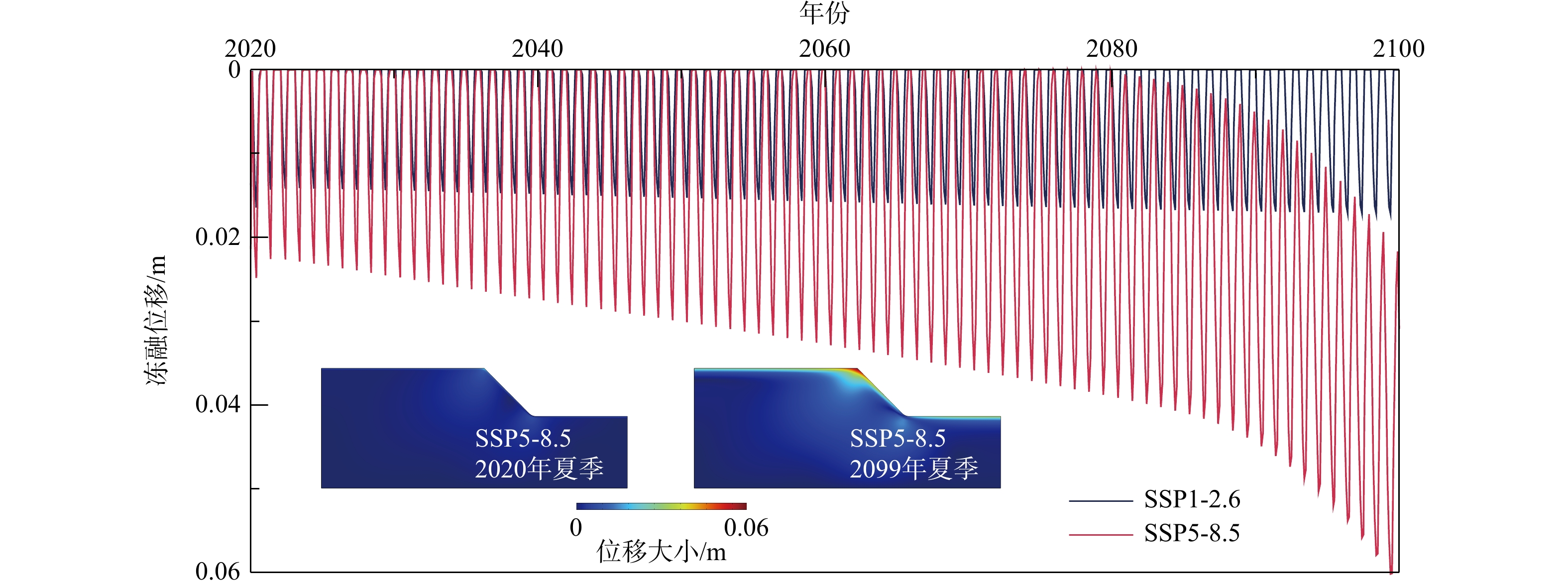
随着大气温度的季节性波动，坡体内部不断地进行着冻结和融化的循环，如图11所示，可以看出，坡体内部的冻融过程主要发生于浅表土体区域，这些随着季节性波动而产生暖季融化、冷季冻结的土体普遍被称为“季节性冻土”或“活动层”。与之相对应，常年不发生融化的冻土则称为“永久冻土”。由图11可见，在SSP1-2.6情景下，升温至2100年，冻结区占比的上下限在季节性波动过程中基本保持不变，即无显著的冻结区退化现象。而在SSP5-8.5情景下，自2020年至2100年，随着坡体温度在气候变暖进程中不断升高，坡体内部冻结区占比的上限和下限均出现明显的下降。最大冻结区占比的下降表明“永久冻土”在逐渐开始消融而转变成“季节性冻土”；最小冻结区占比的下降表明部分活动层逐渐转变为不冻结区域，活动层不断向深部移动。同时，SSP5-8.5情景下冻结区占比曲线在2080年前后出现了一个明显的拐点，2080年之前，尽管年内最小冻结区占比在不断减少，但最大冻结区占比基本没有下降趋势（始终等于1），即在此之前暖季消融的冻结区能够完全在冷季冻结恢复。2080年后（拐点之后），年内冻结区最大占比开始出现明显的退化。同时，略晚于冻结区最大占比出现下降的拐点，在2090年前后，冻结区占比的上下限均出现加速下降的拐点。这样的转变表明，升温至2080年前后，暖季消融的冻结区开始无法完全在冷季冻结恢复，即部分“季节性冻土”出现了永久性消退，转变为永久不冻土。升温至2090年前后，热融的作用将更高效地深入深部的“永久冻土”，使“永久冻土”的退化出现显著加速。位于2080年和2090年这2个拐点的出现不是互相独立的，而是通过实际物理过程联系在一起的。上部“季节性冻土”的消退导致大气温度在向土体内部传递的过程中需要提供更少的潜热，从而同样的热量能够使更深部的土体获得更多的热量，进而加快了冻土消退的进程。因此“永久冻土”加速下降的拐点在时间上并不与“季节性冻土”开始加速下降一致，而是在出现季节性大规模退化之后。在2020-2100年持续80 a的温度升高作用下，坡体内部冻结区将产生6%的消退，由图11可见，在2099年夏季，坡体的融化区深度要显著深于2020年夏季。

图 11 升温情景下含冰冰碛土斜坡冻结区占比演化特征

Figure 11. Evolution characteristics of frozen area proportion of ice-rich moraine slopes under climate warming

下载: 全尺寸图片幻灯片

（3）冻融位移演化特征

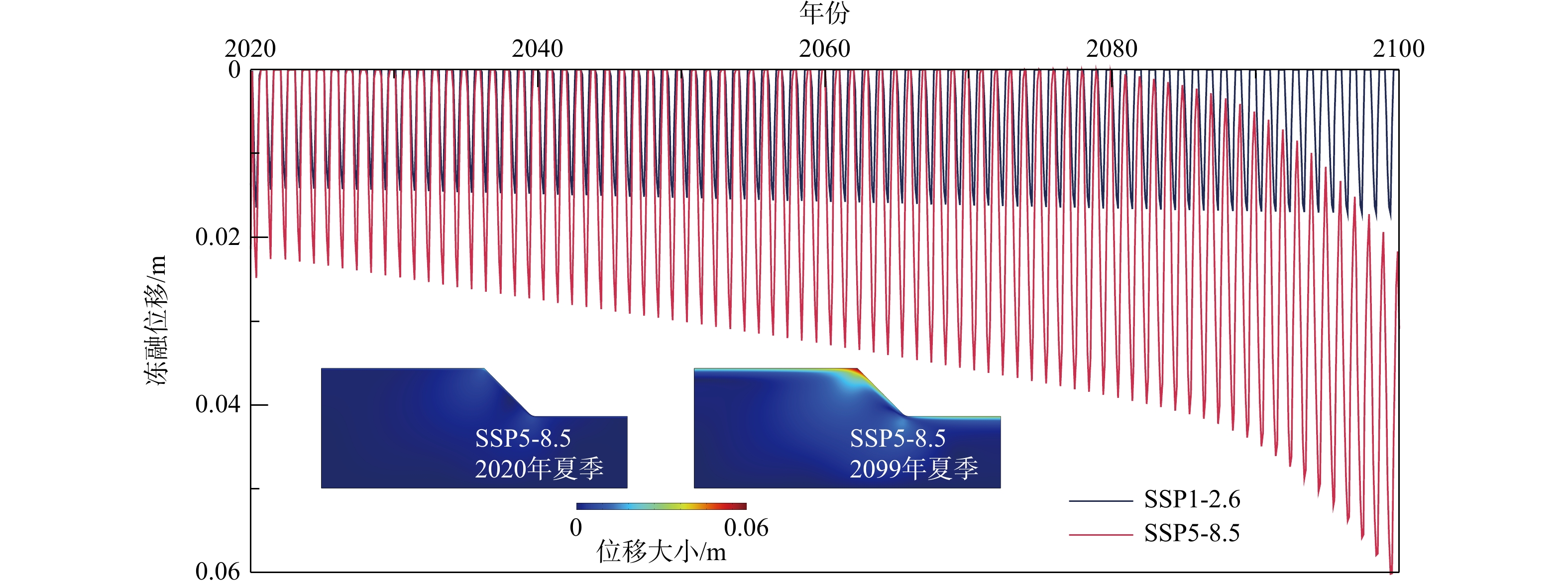
坡体季节性的冻结融化过程中水与冰之间物态的转换导致土体内部会出现冻结膨胀应变或融化沉降应变，导致整个坡体出现冻结膨胀及融化沉降现象。图12统计了2种气候情景下2020-2100年含冰冰碛土斜坡的冻融位移演化。由于冻融位移主要取决于坡体内部的冻结或融化状态以及冻结或融化土体各自的占比，因而位移的演化与冻结区占比的演化具有同样的特征规律。由于坡体季节性冻融过程集中发生于坡体浅表区域，相应地，坡体冻融位移也集中出现在坡体顶部（见冻融位移云图）。在SSP5-8.5情景下，坡体在不断经历季节性“冷季冻结膨胀-暖季融化沉降”循环的同时，持续的升温过程导致坡体融化使坡体逐渐出现了不可逆转的沉降。这一不可逆转的过程主要表现在融化沉降位移逐年增加而冻结膨胀位移基本没有增长，甚至在后期阶段，每年的冻结膨胀量在逐渐下降，这也与上文所描述的冻土退化趋势高度一致。以计算的第一年位移状态为起始点，在SSP5-8.5情景下升温至2080年前后，随着冻结区开始逐渐出现永久性消退，坡体将开始出现不可逆转的热融沉降，直至2100年，坡体年内最大沉降量可达0.06 m。

图 12 升温情景下含冰冰碛土斜坡冻融位移演化图

Figure 12. Evolution of freeze-thaw displacement of ice-rich moraine slope under climate warming

下载: 全尺寸图片幻灯片

3.4 稳定性演化规律

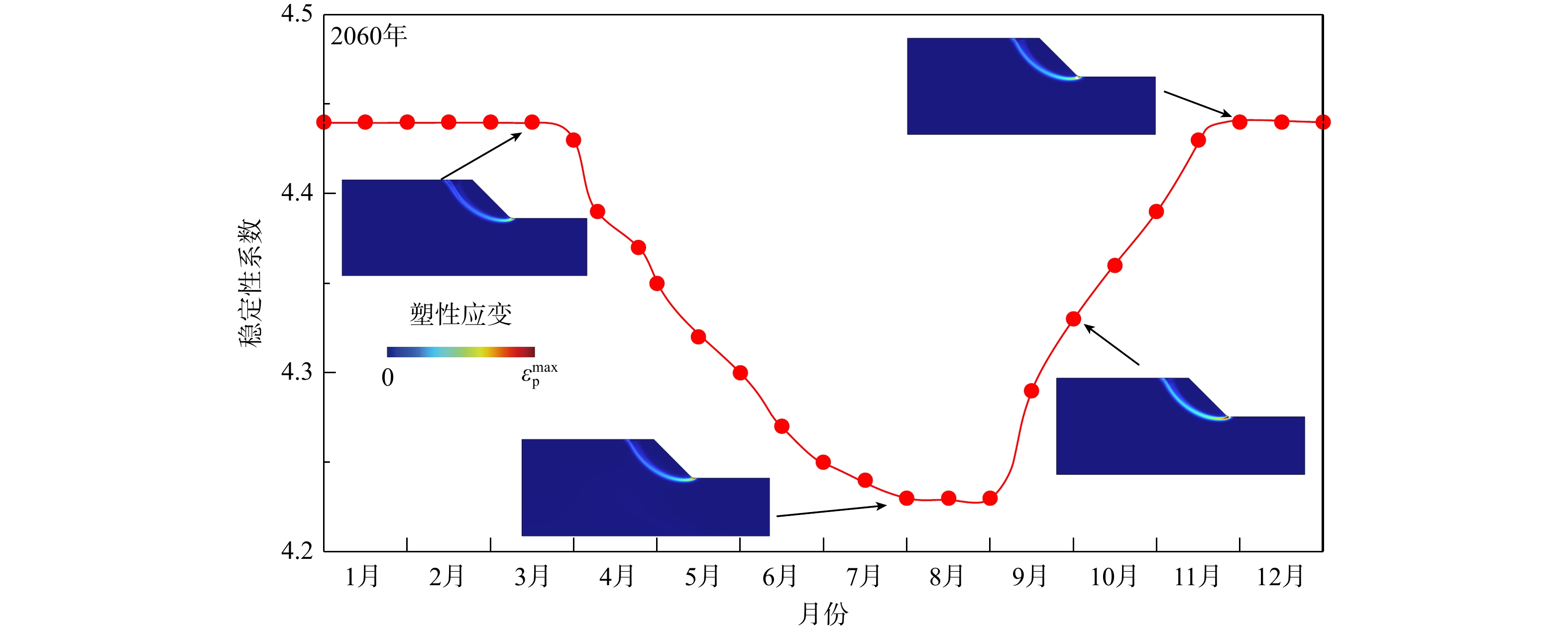
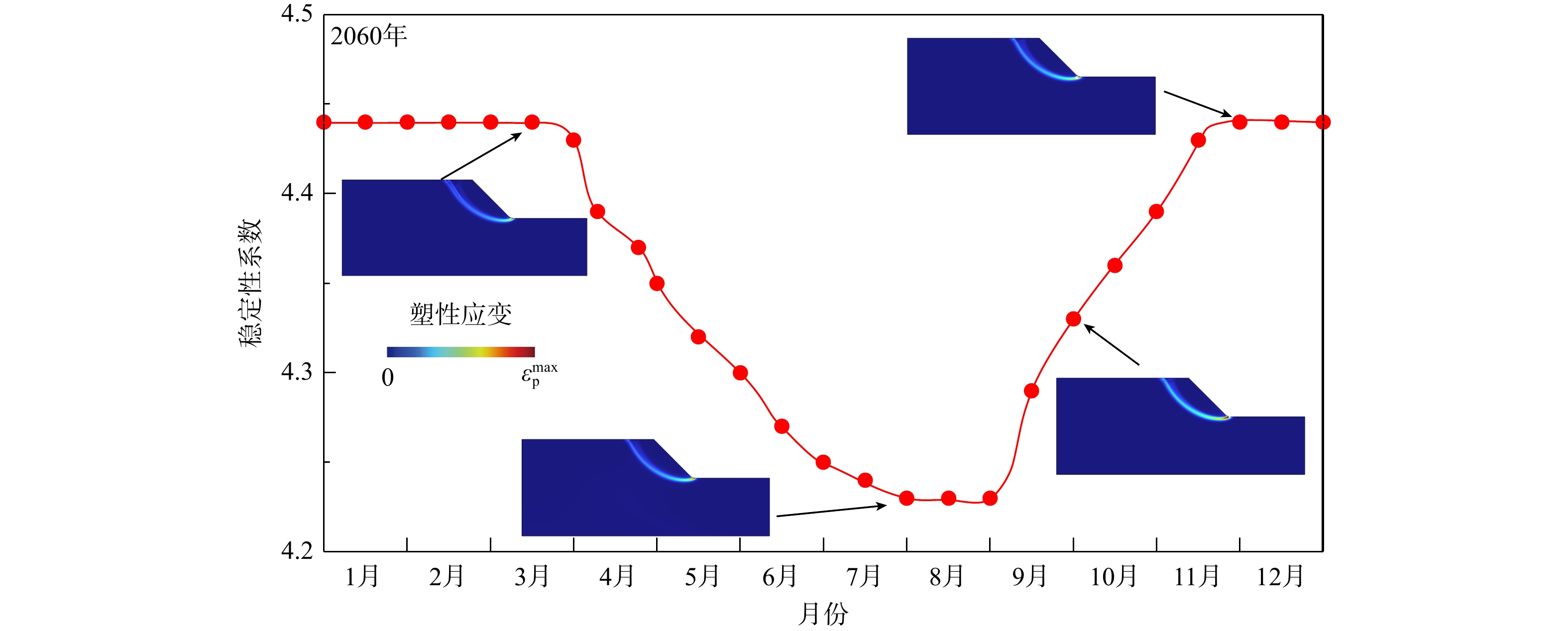
随着斜坡内部季节性的冻融过程，坡体内部土体的强度将相应随之波动。具体表现为，冷季降温冻结，土体强度高；暖季升温融化，土体强度低。因而，坡体的整体稳定性将同样发生季节性的波动。以SSP5-8.5情景下升温至2060年为例，在一年的季节性波动周期中，稳定性的波动曲线整体呈现近似“V”型（图13），稳定性系数在达到年内最低点之后随即出现上升，随后在冷季以较高稳定性保持稳定。同时，如图13所示，在年内的稳定性演化过程中，稳定性的下降过程与上升过程的演化曲线存在一定的非对称现象，表现为下降过程较为缓慢，经历时间较长；而上升过程演化速度相对较为迅速。

图 13 升温情景下2060年含冰冰碛土斜坡稳定性波动示意图

Figure 13. Diagram of ice-rich moraine slope stability seasonal fluctuation during 2060 under climate warming

下载: 全尺寸图片幻灯片

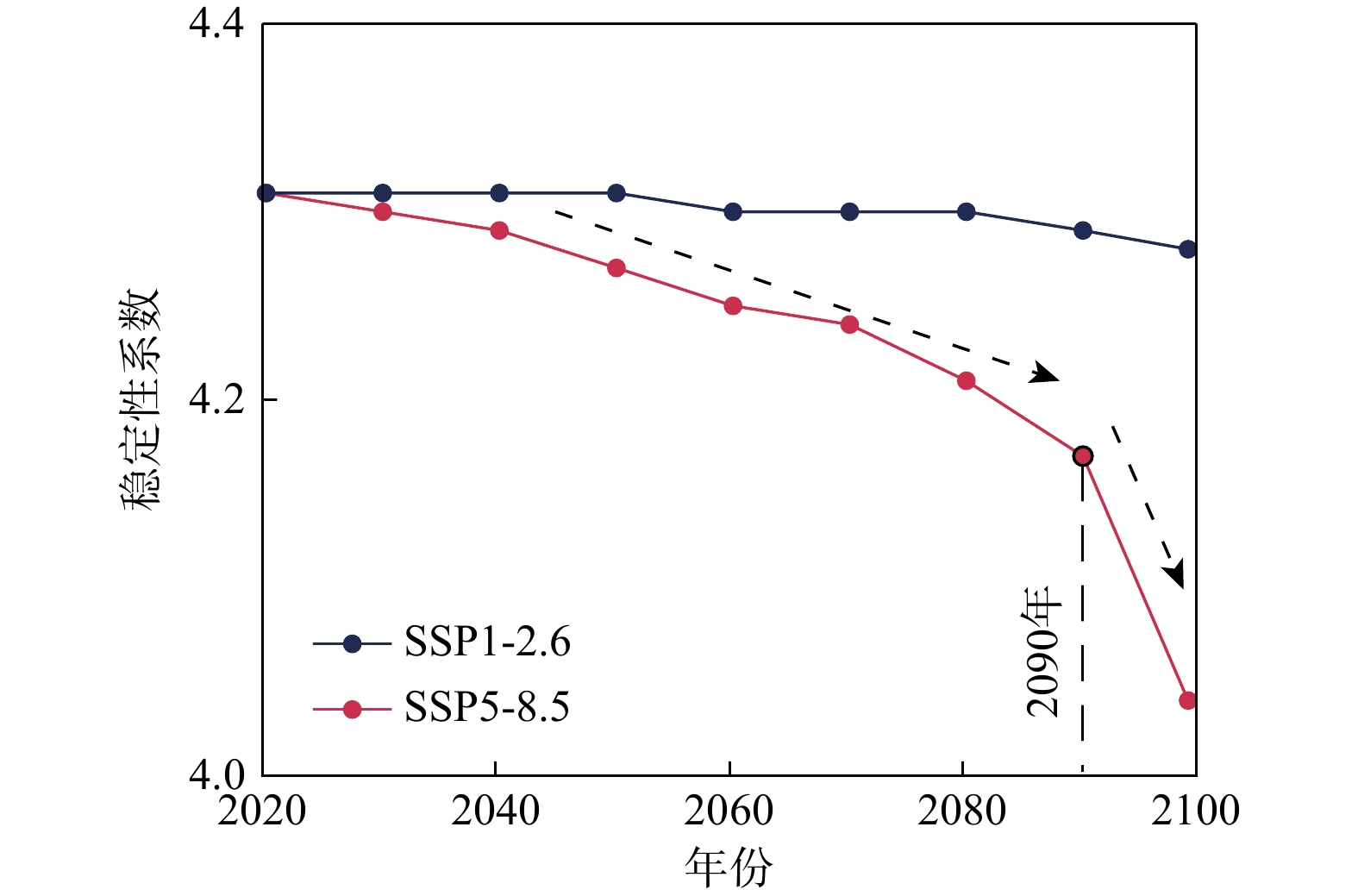
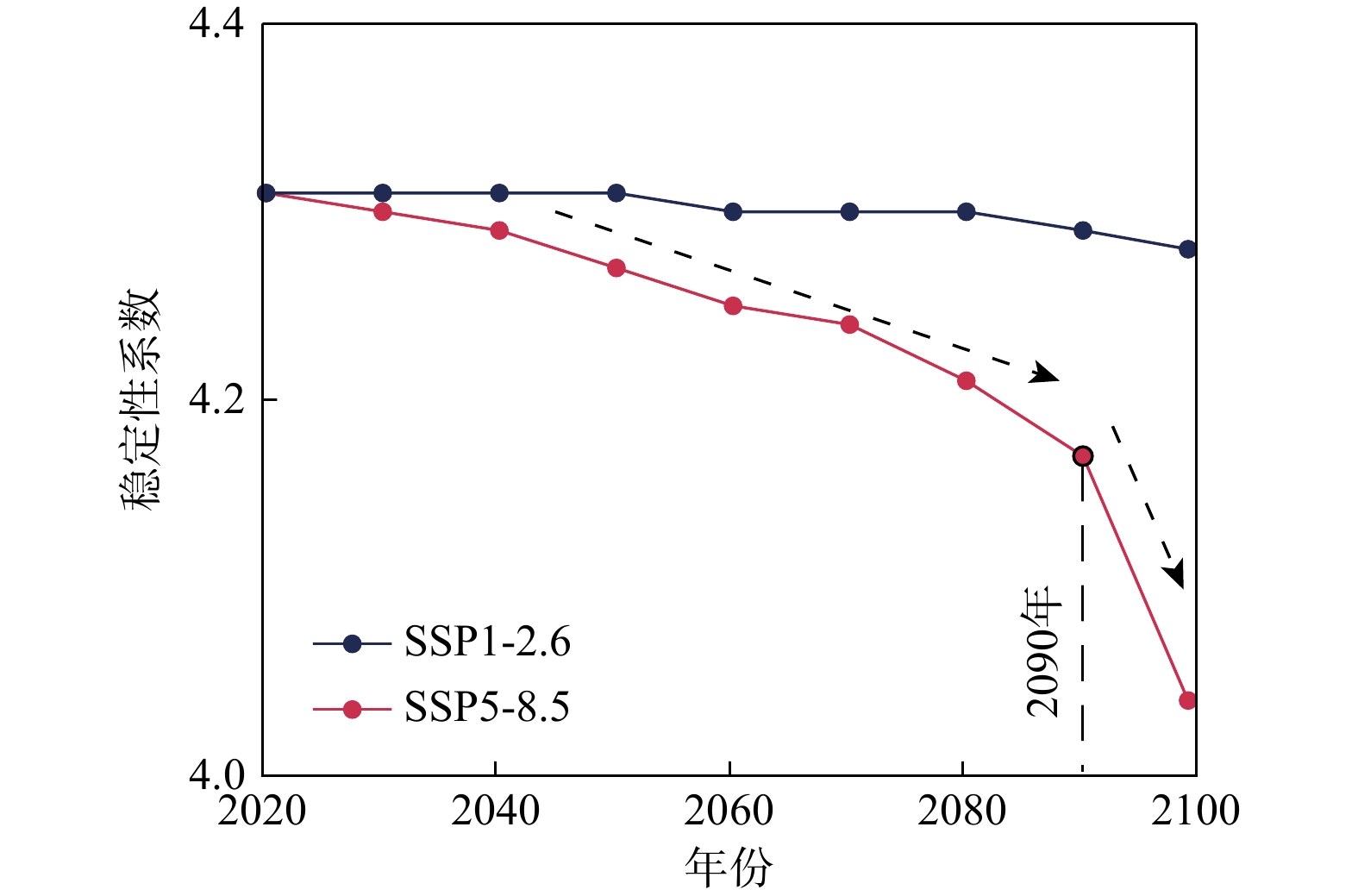
图14统计了2种气候情景下2020-2100年期间坡体年内最差稳定性（夏季所对应的稳定性）的演化过程。坡体的稳定性出现了较为明显的下降且与冻结区占比的下降趋势基本一致（图11）。如3.3节所介绍，在SSP1-2.6情景下，坡体内部冻结区未出现显著的退化，相应地，在该情景下，直至2100年，坡体最差稳定性并未出现显著的下降。而在SSP5-8.5情景下，坡体最差稳定性出现了显著的下降。同时，坡体内部冻结区占比在2090年前后开始出现加速下降，相应地，坡体的最差稳定性在2090前后同样出现加速下降的拐点。这不仅表明坡体的稳定性受控于坡体内部冻结区占比的数量，还揭示了季节性冻土的不断退化以及活动层的不断下移将导致坡体稳定性的下降逐渐出现显著的由量变转向质变的非线性演化特征。由此可以推断，随着热融作用所产生影响的深度不断增加，升温过程对坡体稳定性的削弱作用将更加显著，同样的升温幅度将导致更大程度的稳定性下降，即稳定性在升温过程中出现加速下降的现象，基于该认识可以推断，在更长的时间尺度上，坡体的稳定性将持续地保持加速下降的趋势。统计表明，从2020年至2100年，在两种气候情景下，坡体稳定性系数分别下降了0.7%与6.3%，由此可见不同气候演变模式对于含冰冰碛土斜坡的稳定状况影响显著，更激进的温度升高情景将给如含冰冰碛土斜坡等寒区岩土体的稳定状况带来更大的威胁。这一发现在一定程度上为未来社会经济的可持续发展从而改善气候变暖进程提供了参考依据。

图 14 升温情景下含冰冰碛土斜坡夏季稳定性演化特征

Figure 14. Stability (at summer time) evolution characteristics of ice-rich moraine slopes under climate warming

下载: 全尺寸图片幻灯片

需要说明的是，本研究对于稳定性的探讨是侧重于演化规律的分析。在选取的概念模型和参数设定下，在未来近100 a的气候变化下，坡体稳定性系数并没有下降至1以下，这一方面是由所模拟坡体初始状态较为稳定所致，另一方面来自于该模型计算过程中主要着眼于长时间尺度的温度升高进程对坡体稳定性的影响作用，尚未考虑降雨、冰川融水等复杂边界条件，以及极端高温天气、极端降雨等极端突发气候事件所可能导致的坡体稳定性下降过程。值得说明的是，针对上述复杂水热边界条件以及极端气候事件对坡体稳定性的影响作用与影响机制的研究尚少，本研究也将在探明温度对坡体稳定性的影响机制的基础上，在未来的研究工作中考虑更综合全面的寒区斜坡孕灾致灾模型。

4. 结论与展望

（1）在持续的气候变暖的进程中，含冰冰碛土斜坡显著地响应大气温度升高，在持续升温作用下，60 m深度处土体在SSP1-2.6与SSP5-8.5情况下温度将分别升高0.38℃和1.90℃。随着土体的持续升温，坡体内部将逐渐出现冻结区的退化，该退化包括“季节性冻土”的消失与“永久冻土”向“季节性冻土”的转变。

（2）随着气候季节性波动，坡体内部相应存在持续的冻融循环过程，同时也伴随着周期性的“冻胀-融降”循环不断改变着坡体的形态。在SSP5-8.5情景下升温至2080年前后，大气温度抬升了3.84 ℃，坡体将出现明显的活动层下移现象，与之同时，坡体将出现不可逆转的永久性沉降。

（3）坡体浅表季节性冻土的存在可作为“永久冻土”遭受变暖冲击下的缓冲地带，通过在暖季吸收大量潜热保持“永久冻土”的存在。在SSP5-8.5情景下，2080年坡体活动层开始出现永久消退之后，大气环境与坡体内部土体将进行影响范围更深、效率更高的热交换作用，导致在2090年前后，坡体内部的“永久冻土”开始加速消退。

（4）在持续的升温作用下，含冰冰碛土斜坡在最不利工况下的稳定性将随着坡体内部冻结区的消退而相应地下降，直至2100年，在SSP1-2.6与SSP5-8.5情景下，坡体的夏季稳定性系数分别下降了0.7%与6.3%。在持续的升温作用下，坡体稳定性的下降过程将出现显著的非线性演化特征，这一特征不仅与坡体内部冻结区的占比相关，还与坡体内热融过程的作用深度有关。

本研究通过数值模拟初步探知了寒区含冰冰碛土斜坡在温度升高作用下水热力耦合特征的响应过程以及坡体稳定性的演化过程，为精细化探究寒区复杂水热条件下各类复杂地质体的物理力学演化过程奠定了模拟技术上以及认知上的基础。同时，针对寒区岩土体的相关地质灾害，还有更多的相关科学问题亟待解决，在此展望如下：

（1）更复杂的水热条件下地质体长演化特征探究。如冰湖-冰碛坝结构、热融喀斯特湖等诸多寒区地质体由于其复杂的水文地质环境以及水热条件，内部的物理力学演化过程将更加复杂。因而今后需要开展更多针对性的现场调查、室内外试验以及数值模拟和理论分析工作，对其物理力学过程及多物理场耦合演化特征进行更精细化的表征刻画。

（2）更全面灾害链触发机制及致灾过程研究。高寒地区的滑坡灾害往往具有规模大、运移距离长的特点，这一特征极易导致在滑坡运移堆积过程中形成次生灾害以及触发巨型灾害链，如堰塞堵江、漫顶溃坝以及大型山地泥石流等。如何合理正确地对该类灾害链的形成及演化发展过程进行探究仍是如今亟待解决的科学问题。

所有作者声明不存在利益冲突。

The authors declare that no competing interests exist.

图 1 研究区灾害点分布概况（滑坡灾害点源自文献[8,33]调研汇编）

Figure 1. Distribution of hazard sites in the study area (Landslide locations are derived from a large number of literature [8,33] research and compilation)

下载: 全尺寸图片幻灯片

图 2 波密地区2018-2020气温波动特征及根据海拔差修正后的研究区气温波动特征

Figure 2. Temperature fluctuation characteristics of Bomê County from 2018 to 2020 and the temperature fluctuation characteristics of the study area corrected according to altitude difference

下载: 全尺寸图片幻灯片

图 3 SSP1-2.6与SSP5-8.5情景下波密地区2020-2100气温抬升示意图

Figure 3. Schematic diagram of temperature rise in Bomê County from 2020 to 2100 under SSP1-2.6 and SSP5-8.5 scenarios

下载: 全尺寸图片幻灯片

图 4 考虑冰水相变作用下传热-渗流-变形耦合示意图（实线表示本模型中所考虑的耦合作用，虚线表示本模型所忽略的耦合作用）

下载: 全尺寸图片幻灯片

图 5 冰水相变过程示意图

θ_i，θ_w分别为孔隙中冰、水的体积分数；T_pc为相变温度；∆T为地温梯度

Figure 5. Schematic diagram of ice-water phase transition process

下载: 全尺寸图片幻灯片

图 6 数值模型验证对比

数据点为JAME^[43]试验结果；虚线为HUANG等^[45]数值模拟验证结果；实线为本研究所建立数值模型的验证结果

Figure 6. Comparison of numerical model verification

下载: 全尺寸图片幻灯片

图 7 寒区含冰冰碛土斜坡致灾机理示意图

Figure 7. Conceptual diagram of hazard-causing mechanism of ice-rich moraine landslide in cold regions

下载: 全尺寸图片幻灯片

图 8 模型几何与边界条件以及网格剖分示意图

注：T为大气温度；T₀为初始年份平均气温；ω为角频率；φ为波动函数初相位； $\Delta T$ 为升温速率；t为时间；A为温度波动幅值的1/2

Figure 8. Schematic diagram of model geometry and boundary conditions and grid generation

下载: 全尺寸图片幻灯片

图 9 不同温度升高情景下2060年含冰冰碛土斜坡地温分布特征

Figure 9. Characteristics of ground temperature distribution in ice-rich moraine slopes under different climate warming during 2060

下载: 全尺寸图片幻灯片

图 10 不同温度升高情景下2020-2100年含冰冰碛土斜坡地温分布演化特征

Figure 10. Evolution characteristics of ground temperature distribution in ice-rich moraine slopes under different warming scenarios

下载: 全尺寸图片幻灯片

图 11 升温情景下含冰冰碛土斜坡冻结区占比演化特征

Figure 11. Evolution characteristics of frozen area proportion of ice-rich moraine slopes under climate warming

下载: 全尺寸图片幻灯片

图 12 升温情景下含冰冰碛土斜坡冻融位移演化图

Figure 12. Evolution of freeze-thaw displacement of ice-rich moraine slope under climate warming

下载: 全尺寸图片幻灯片

图 13 升温情景下2060年含冰冰碛土斜坡稳定性波动示意图

Figure 13. Diagram of ice-rich moraine slope stability seasonal fluctuation during 2060 under climate warming

下载: 全尺寸图片幻灯片

图 14 升温情景下含冰冰碛土斜坡夏季稳定性演化特征

Figure 14. Stability (at summer time) evolution characteristics of ice-rich moraine slopes under climate warming

下载: 全尺寸图片幻灯片

表 1 物理力学参数表

Table 1. Physical and mechanical parameters

参数	数值	描述
ρ_s	2600 kg/m³	土体基质密度
ρ_w	1000 kg/m³	水体密度
ρ_i	918 kg/m³	冰体密度
ε₀	0.15	孔隙率
ε_r	0.05	残余含水率
k_u	4×10⁻¹¹ m²	融土渗透系数
μ	1.793×10⁻³ Pa·s	水体动力黏度
Ω	50	冰体阻抗系数
λ_s	1.07 W/(m·℃)	土体导热系数
λ_w	0.63 W/(m·℃)	水体导热系数
λ_i	2.31 W/(m·℃)	冰体导热系数
C_s	0.93 kJ/(kg·℃)	土体热容
C_w	4.2 kJ/(kg·℃)	水体热容
C_i	2.1 kJ/(kg·℃)	冰体热容
L	334.56 kJ/kg	冰水相变潜热
E_s	100 MPa	土体杨氏模量
$\nu$	0.4	土体泊松比
c_un	60 kPa	融土黏聚力
c_f	200 kPa	冻土黏聚力
φ_un	25 °	融土内摩擦角
φ_f	30 °	冻土内摩擦角

下载: 导出CSV

参考文献(46)

[1]	FAN X,DUAN Q,SHEN C,et al. Global surface air temperatures in CMIP6:Historical performance and future changes[J]. Environmental Research Letters,2020,15(10):104056.
[2]	Mountain Research Initiative EDW Working Group. Elevation-dependent warming in mountain regions of the world[J]. Nature Climate Change,2015,5(5):424-430. doi: 10.1038/nclimate2563
[3]	BISKABORN B K,SMITH S L,NOETZLI J,et al. Permafrost is warming at a global scale[J]. Nature Communications,2019,10(1):264. doi: 10.1038/s41467-018-08240-4
[4]	NITZBON J,WESTERMANN S,LANGER M,et al. Fast response of cold ice-rich permafrost in northeast Siberia to a warming climate[J]. Nature Communications,2020,11(1):2201. doi: 10.1038/s41467-020-15725-8
[5]	YOU Q,CAI Z,PEPIN N,et al. Warming amplification over the Arctic Pole and Third Pole:Trends,mechanisms and consequences[J]. Earth-Science Reviews,2021,217:103625. doi: 10.1016/j.earscirev.2021.103625
[6]	ZHANG G,YAO T,XIE H,et al. An inventory of glacial lakes in the Third Pole region and their changes in response to global warming[J]. Global and Planetary Change,2015,131:148-157. doi: 10.1016/j.gloplacha.2015.05.013
[7]	ZHAO L,PING C L,YANG D,et al. Changes of climate and seasonally frozen ground over the past 30 years in Qinghai-Xizang (Tibetan) Plateau,China[J]. Global and Planetary Change,2004,43(1/2):19-31. doi: 10.1016/j.gloplacha.2004.02.003
[8]	崔鹏,郭剑. 沟谷灾害链演化模式与风险防控对策[J]. 工程科学与技术,2021,53(3):5-18. CUI P,GUO J. Evolution models,risk prevention and control counter measures of the valley disaster chain[J]. Advanced Engineering Science,2021,53(3):5-18. (in Chinese with English abstract
[9]	NEUPANE R,CHEN H,CAO C. Review of moraine dam failure mechanism[J]. Geomatics,Natural Hazards and Risk,2019,10(1):1948-1966. doi: 10.1080/19475705.2019.1652210
[10]	RICHARDSON S D,REYNOLDS J M. Degradation of ice-cored moraine dams :Implications for hazard development[M]. Wallingford:IAHS Press,2000.
[11]	HEALY T R. Thermokarst:A mechanism of de-icing ice-cored moraines[J]. Boreas,2008,4(1):19-23.
[12]	HAEBERLI W,HUDER J,KEUSEN H,et al. Core drilling through rock glacier permafrost[C]//Anon. Proceedings of the Fith International Conference on Permafrost. [S. 1. ]:[S. n. ],1988:937-942.
[13]	李德基,游勇. 西藏波密米堆冰湖溃决浅议[J]. 山地研究,1992,10(4):219-224. LI D J,YOU Y. Analysis on the outburst of the glacial lake in Bome Midui,Tibet[J]. Mountain Research,1992,10(4):219-224. (in Chinese with English abstract
[14]	刘建康,张佳佳,高波,等. 我国西藏地区冰湖溃决灾害综述[J]. 冰川冻土,2019,41(6):1335-1347. LIU J K,ZHANG J J,GAO B,et al. An overview of glacial lake outburst flood in Tibet,China[J]. Journal of Glaciology and Geocryology,2019,41(6):1335-1347. (in Chinese with English abstract
[15]	王欣,蒋亮虹,刘时银,等. 喜马拉雅山北坡冰碛湖坝温度特征及其对堤坝稳定的影响[J]. 冰川冻土,2014,36(6):1517-1525. WANG X,JIANG L H,LIU S Y,et al. Temperature features of a moraine-dam on north slopes of the Himalayas and their effect on the dam stability[J]. Journal of Glaciology and Geocryology,2014,36(6):1517-1525. (in Chinese with English abstract
[16]	蒋婷婷,潘华利,艾一帆,等. 冻融循环及含水率对冰碛土力学特性影响[J]. 地质科技通报,2024,43(2):238-252. JIANG T T,PAN H L,AI Y F et al. ,Effect of freeze-thaw cycles and water content on the mechanical properties of moraine soil[J]. Bulletin of Geological Science and Technology,2024,43(2):238-252. (in Chinese with English abstract
[17]	高波,张佳佳,王军朝,等. 西藏天摩沟泥石流形成机制与成灾特征[J]. 水文地质工程地质,2019,46(5):144-153. GAO B,ZHANG J J,WANG J C,et al. Formation mechanism and disaster characteristics of debris flow in the Tianmo gully in Tibet[J]. Hydogeology & Engineering Geology,2019,46(5):144-153. (in Chinese with English abstract
[18]	MCROBERTS E C,MORGENSTERN N R. The stability of thawing slopes[J]. Canadian Geotechnical Journal,1974,11(4):447-469. doi: 10.1139/t74-052
[19]	王绍令. 青藏公路风火山地区的热融滑塌[J]. 冰川冻土,1990,12(1):63-70. WANG S L. Thermal melt collapse in Feng-volcano area of Qinghai-Tibet Highway[J]. Journal of Glaciology and Geocryology,1990,12(1):63-70. (in Chinese with English abstract
[20]	靳德武,牛富俊,李宁. 青藏高原多年冻土区热融滑塌变形现场监测分析[J]. 工程地质学报,2006,14(5):677-682. doi: 10.3969/j.issn.1004-9665.2006.05.019 JIN D W,NIU F J,LI N. In-situ monitoring and analysis of thaw slumping and deformation in gentle slopeing ground of permafrost soils on Qinghai-Tibet Plateau[J]. Journal of Engineering Geology,2006,14(5):677-682. (in Chinese with English abstract doi: 10.3969/j.issn.1004-9665.2006.05.019
[21]	SHAN W,ZHANG C C,GUO Y. Mechanism of shallow slide on soil road cutting slope during spring in seasonal frozen region[J]. Applied Mechanics and Materials,2012,178/181:1258-1263. doi: 10.4028/www.scientific.net/AMM.178-181.1258
[22]	王超. 季冻区哈大高铁边坡冻融滑塌机理研究[D]. 哈尔滨:哈尔滨工业大学,2014. WANG C. Research on freeze-thaw slumping mechanism of harbin-dalian high-speed railway slope in seasonally frozen soil region[D]. Harbin:Harbin Institute of Technology,2014. (in Chinese with English abstract
[23]	KORSHUNOV A A,DOROSHENKO S P,Nevzorov A L. The impact of freezing-thawing process on slope stability of earth structure in cold climate[J]. Procedia Engineering,2016,143:682-688. doi: 10.1016/j.proeng.2016.06.100
[24]	李智明. 冻土水热力场耦合机理研究与工程应用[D]. 哈尔滨:哈尔滨工业大学,2017. LI Z M. Study on mechanisum of moisture-heat-stress coupling for frozen soil and engineering application[D]. Harbin:Harbin Institute of Technology,2017. (in Chinese with English abstract
[25]	CUI K,QIN X. Landslide risk assessment of frozen soil slope in Qinghai-Tibet Plateau during spring thawing period under the coupling effect of moisture and heat[J]. Natural Hazards,2023,115(3):2399-2416. doi: 10.1007/s11069-022-05646-8
[26]	GE Q,WU H,GONG Y F. Research on the soil slope stability based on soil strength deterioration in seasonal frozen areas[J]. Advanced Materials Research,2011,243/249:4270-4273. doi: 10.4028/www.scientific.net/AMR.243-249.4270
[27]	李书林,张哲华,陈鑫鑫,等. 浅析冻融循环作用下青藏高原冻土区软弱结构面长期稳定性[J]. 科学技术创新,2020(26):129-130. doi: 10.3969/j.issn.1673-1328.2020.26.058 LI S L,ZHANG Z H,CHEN X X,et al. Analysis on the long-term stability of weak structural plane in the frozen soil region of Qinghai-Tibet Plateau under the action of freeze-thaw cycle[J]. Science and Technology Innovation,2020(26):129-130. (in Chinese with English abstract doi: 10.3969/j.issn.1673-1328.2020.26.058
[28]	KAWAMURA S,MIURA S. Stability evaluation of volcanic slope subjected to rainfall and freeze-thaw action based on field monitoring[J]. Advances in Civil Engineering,2011(1):1-14.
[29]	NIU F,LUO J,LIN Z,et al. Thaw-induced slope failures and stability analyses in permafrost regions of the Qinghai-Tibet Plateau,China[J]. Landslides,2016,13(1):55-65. doi: 10.1007/s10346-014-0545-2
[30]	XU J,WANG Z Q,REN J W,et al. Mechanism of slope failure in loess terrains during spring thawing[J]. Journal of Mountain Science,2018,15(4):845-858. doi: 10.1007/s11629-017-4584-8
[31]	宋勇军,操警辉,程柯岩,等. 砂岩冻结/解冻过程蠕变特性研究[J]. 水文地质工程地质,2024,51(6):93-103. SONG Y J,CAO J H,CHENG K Y,et al. Creep characteristics of sandstone durir:g freezing/thawing process[J]. Hydrogeology & Engineering Geology,2024,51(6):93-103.(in Chinese with English abstract
[32]	陈兰,范宣梅,熊俊麟,等. 藏东南多依弄巴流域冰湖溃决危险性评价[J]. 地质科技通报,2023,42(2):258-266. CHEN L,FAN X M,XIONG J L,et al. Hazard assessment of glacial lake outbursts in the Doyinongba Basin,southeastern Tibetan Plateau[J]. Bulletin of Geological Science and Technology,2023,42(2):258-266. (in Chinese with English abstract
[33]	郭长宝,吴瑞安,蒋良文,等. 川藏铁路雅安-林芝段典型地质灾害与工程地质问题[J]. 现代地质,2021,35(1):1-17. GUO C B,WU R A,JIANG L W,et al. Typical geohazards and engineering geological problems along the Ya'an-Linzhi section of the Sichuan-Tibet Railway,China[J]. Geoscience,2021,35(1):1-17. (in Chinese with English abstract
[34]	GROVE J M. Little ice ages:Vol. 2[M]. Ed2. Routledge:[S. n. ],2013.
[35]	焦世晖,王凌越,刘耕年. 全球变暖背景下青藏高原多年冻土分布变化预测[J]. 北京大学学报(自然科学版),2016,52(2):249-256. JIAO S H,WANG L Y,LIU G N. Prediction of Tibetan Plateau permafrost distribution in global warming[J]. Acta Scientiarum Naturalium Universitatis Pekinensis,2016,52(2):249-256. (in Chinese with English abstract
[36]	李述训,吴通华. 青藏高原地气温度之间的关系[J]. 冰川冻土,2012,27(5):627-632. LI S X,WU T H. The relationship between earth,air and temperature in Qinghai-Tibet Plateau[J]. Journal of Glaciology and Geocryology,2012,27(5):627-632. (in Chinese with English abstract
[37]	O’NEILL B C,TEBALDI C,VAN VUUREN D P,et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6[J]. Geoscientific Model Development,2016,9(9):3461-3482. doi: 10.5194/gmd-9-3461-2016
[38]	GRENIER C,ANBERGEN H,BENSE V,et al. Groundwater flow and heat transport for systems undergoing freeze-thaw:Intercomparison of numerical simulators for 2D test cases[J]. Advances in Water Resources,2018,114:196-218.
[39]	MCKENZIE J M,VOSS C I,SIEGEL D I. Groundwater flow with energy transport and water-ice phase change:Numerical simulations,benchmarks,and application to freezing in peat bogs[J]. Advances in Water Resources,2007,30(4):966-983. doi: 10.1016/j.advwatres.2006.08.008
[40]	VAN GENUCHTEN M T H. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal,1980,44(5):892-898. doi: 10.2136/sssaj1980.03615995004400050002x
[41]	BIOT M A,Willis D G. The elastic coefficients of the theory of consolidation[J]. Journal of Applied Mechanics,2021,24(4):594-601.
[42]	KURYLYK B L,WATANABE K. The mathematical representation of freezing and thawing processes in variably-saturated,non-deformable soils[J]. Advances in Water Resources,2013,60:160-177. doi: 10.1016/j.advwatres.2013.07.016
[43]	JAME Y W. Heat and mass transfer in freezing unsaturated soil[D]. [S. 1. ]:University of Saskatchewan,1977.
[44]	PENG E X,SHENG Y,HU X Y,et al. Thermal effect of thermokarst lake on the permafrost under embankment[J]. Advances in Climate Change Research,2021,12(1):76-82. doi: 10.1016/j.accre.2020.10.002
[45]	HUANG X,RUDOLPH D L,Glass B. A coupled thermal‐hydraulic‐mechanical approach to modeling the impact of roadbed frost loading on water main failure[J]. Water Resources Research,2022,58(3):e2021WR030933.
[46]	JI H,NAN Z,HU J,et al. On the spin-up strategy for spatial modeling of permafrost dynamics:A case study on the Qinghai-Tibet Plateau[J]. Journal of Advances in Modeling Earth Systems,2022,14(3):e2021MS002750.

施引文献

资源附件(0)

访问统计

点击查看大图

图(14) / 表(1)

计量

文章访问数: 478
PDF下载量: 81
被引次数: 0

1. 研究区概况
1.1 水文地质概况
1.2 气候条件概况
2. 温度-渗流-应力多场耦合方法
2.1 冰水相变过程控制方程
2.2 考虑冰水相变过程下温度-渗流-应力耦合模型
2.3 数值方法有效性验证
3. 含冰冰碛土斜坡水热力耦合特性与稳定性演化规律
3.1 含冰冰碛土斜坡概念模型
3.2 含冰冰碛土斜坡边界条件及初始条件
3.3 水热力耦合特性
3.4 稳定性演化规律
4. 结论与展望

1. 研究区概况
1.1 水文地质概况
1.2 气候条件概况
2. 温度-渗流-应力多场耦合方法
2.1 冰水相变过程控制方程
2.2 考虑冰水相变过程下温度-渗流-应力耦合模型
2.3 数值方法有效性验证
3. 含冰冰碛土斜坡水热力耦合特性与稳定性演化规律
3.1 含冰冰碛土斜坡概念模型
3.2 含冰冰碛土斜坡边界条件及初始条件
3.3 水热力耦合特性
3.4 稳定性演化规律
4. 结论与展望

参考文献(46)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

气候变化环境下青藏高原含冰冰碛土斜坡水热力耦合特性与长期稳定性

doi: 10.19509/j.cnki.dzkq.tb20240079

作者简介:
李奇龙：E-mail：liqilong@cug.edu.cn

通讯作者:
E-mail：jqzhou@whu.edu.cn

计量

Coupling characteristics and stability evolution of ice-rich moraine soil slopes on the Tibetan Plateau under climate change

Author Bio:
E-mail：liqilong@cug.edu.cn

Corresponding author: E-mail：jqzhou@whu.edu.cn

1. 研究区概况

1.1 水文地质概况

1.2 气候条件概况

2. 温度-渗流-应力多场耦合方法

2.1 冰水相变过程控制方程

2.2 考虑冰水相变过程下温度-渗流-应力耦合模型

2.3 数值方法有效性验证

3. 含冰冰碛土斜坡水热力耦合特性与稳定性演化规律

3.1 含冰冰碛土斜坡概念模型

3.2 含冰冰碛土斜坡边界条件及初始条件

3.3 水热力耦合特性

3.4 稳定性演化规律

4. 结论与展望

计量

目录

1. 研究区概况

1.1 水文地质概况

1.2 气候条件概况

2. 温度-渗流-应力多场耦合方法

2.1 冰水相变过程控制方程

2.2 考虑冰水相变过程下温度-渗流-应力耦合模型

2.3 数值方法有效性验证

3. 含冰冰碛土斜坡水热力耦合特性与稳定性演化规律

3.1 含冰冰碛土斜坡概念模型

3.2 含冰冰碛土斜坡边界条件及初始条件

3.3 水热力耦合特性

3.4 稳定性演化规律

4. 结论与展望

留言板

气候变化环境下青藏高原含冰冰碛土斜坡水热力耦合特性与长期稳定性

doi: 10.19509/j.cnki.dzkq.tb20240079

作者简介: 李奇龙：E-mail：liqilong@cug.edu.cn

通讯作者: E-mail：jqzhou@whu.edu.cn

计量

出版历程

Coupling characteristics and stability evolution of ice-rich moraine soil slopes on the Tibetan Plateau under climate change

Author Bio: E-mail：liqilong@cug.edu.cn

Corresponding author: E-mail：jqzhou@whu.edu.cn

1. 研究区概况

1.1 水文地质概况

1.2 气候条件概况

2. 温度-渗流-应力多场耦合方法

2.1 冰水相变过程控制方程

2.2 考虑冰水相变过程下温度-渗流-应力耦合模型

2.3 数值方法有效性验证

3. 含冰冰碛土斜坡水热力耦合特性与稳定性演化规律

3.1 含冰冰碛土斜坡概念模型

3.2 含冰冰碛土斜坡边界条件及初始条件

3.3 水热力耦合特性

3.4 稳定性演化规律

4. 结论与展望

计量

出版历程

目录

1. 研究区概况

1.1 水文地质概况

1.2 气候条件概况

2. 温度-渗流-应力多场耦合方法

2.1 冰水相变过程控制方程

2.2 考虑冰水相变过程下温度-渗流-应力耦合模型

2.3 数值方法有效性验证

3. 含冰冰碛土斜坡水热力耦合特性与稳定性演化规律

3.1 含冰冰碛土斜坡概念模型

3.2 含冰冰碛土斜坡边界条件及初始条件

3.3 水热力耦合特性

3.4 稳定性演化规律

4. 结论与展望

作者简介:
李奇龙：E-mail：liqilong@cug.edu.cn

通讯作者:
E-mail：jqzhou@whu.edu.cn

Author Bio:
E-mail：liqilong@cug.edu.cn