基于物理模型试验的库岸滑坡水阻力系数研究

谢云轩; 汪洋; 王梦瑶; 冯霄; 彭铿; 付昱衡

doi:10.19509/j.cnki.dzkq.tb20240247

基于物理模型试验的库岸滑坡水阻力系数研究

doi: 10.19509/j.cnki.dzkq.tb20240247

谢云轩^1,,
汪洋^1, ,,
王梦瑶¹,
冯霄¹,
彭铿^{2, 3},
付昱衡¹

1.
中国地质大学（武汉）工程学院，武汉 430074
2.
华新水泥股份有限公司，武汉 430035
3.
华新超可隆新型建材科技（黄石）有限公司，湖北黄石 435000

基金项目: 国家自然科学基金项目（42077277）；中国地质大学（武汉）教学试验室开放基金资助项目

详细信息

作者简介:
谢云轩：E-mail：761194047@qq.com

通讯作者:
E-mail：wangyangcug@126.com

中图分类号: P642.22
计量
- 文章访问数: 40
- PDF下载量: 1
- 被引次数: 0
出版历程
- 收稿日期: 2024-05-11
- 录用日期: 2024-07-01
- 修回日期: 2024-06-26
- 网络出版日期: 2025-03-21

Water resistance coefficient of bank slope landslides via physical model experiments

XIE Yunxuan^1
,,
WANG Yang^{1
, ,},
WANG Mengyao¹,
FENG Xiao¹,
PENG Keng^{2, 3},
FU Yuheng¹

1.
Faculty of Engineering, China University of Geosciences (Wuhan), Wuhan 430074, China
2.
Huaxin Cement Co., Ltd., Wuhan 430035, China
3.
Huaxin Chaokelong new building Materials Technology (Huangshi) Co., Ltd., Huangshi Hubei 435000, China

More Information

Author Bio:
E-mail：761194047@qq.com

Corresponding author: E-mail：wangyangcug@126.com

摘要

摘要:
水阻力是影响库岸滑坡运动速度的关键因素之一，为了量化库岸滑坡入水的阻力计算，并进一步为库岸滑坡入水速度的分析提供试验数据和理论基础，设计了入水阻力系数的测试试验，基于水下试块动力学与运动学方程建立了水阻力系数计算模型。采用无量纲化分析方法对试验结果进行了分析，研究了各无量纲因子对水阻力系数的影响，通过多元线性回归分析得出了水阻力系数理论公式。以2018年10月11日西藏自治区达江县白格滑坡第1次滑坡为例，应用水阻力系数理论公式对白格滑坡速度进行了计算，并与其他方法得出的速度计算结果进行了对比分析。结果表明：随着相对速度的增加，水阻力系数整体呈现先上升后下降的趋势；随着相对横截面积增加，水阻力系数减小。水阻力系数理论公式的拟合度R²=0.77，表明理论公式具有较好准确度。与现有计算结果相比，在考虑水阻力的情况下白格滑坡最大运动速度减小了23.5%，最大速度差值为8.5 m/s，最大速度时刻延后了7.7 s。研究提出了水阻力系数计算模型，初步解决了水阻力系数取值困难的问题，有利于提高库岸滑坡入水速度的预测精度。
- 物理模型试验 /
- 库岸滑坡 /
- 滑坡速度计算 /
- 水阻力系数 /
- 白格滑坡
Abstract: Objective
Hydrodynamic resistance is one of the key factors influencing the velocity of landslides entering water. To quantify the resistance experienced by reservoir bank landslides upon water entry and provide experimental data and a theoretical basis for analyzing their entry velocity, this study designed an experiment to measure the water entry resistance coefficient.
Methods
Based on the dynamics and kinematics equations of submerged test blocks, a comprehensive calculation model for the water resistance coefficient was established. The experimental results were analyzed using dimensionless analysis methods to investigate the effects of various dimensionless factors on the water resistance coefficient. A multiple linear regression analysis was conducted to derive the comprehensive water resistance coefficient calculation model. Taking the Baige landslide of October 11, 2018, as a case study, the velocity of the Baige landslide was calculated using the theoretical formula for the water resistance coefficient, and the results were compared with those obtained from other methods.
Results
The results indicate that as relative velocity increases, the comprehensive water resistance coefficient initially rises and then decreases. Additionally, as the relative cross-sectional area increases, the comprehensive water resistance coefficient decreases. The theoretical formula for the water resistance coefficient has a coefficient of determination (R²) of 0.77, demonstrating good accuracy. Compared to existing calculation results, considering hydrodynamic resistance, the maximum movement speed of the Baige landslide decreased by 23.5%, with a maximum speed difference of 8.5 m/s, and the time at which the maximum speed occurred was delayed by 7.7 seconds.
Conclusion
This study proposes a comprehensive calculation model for the water resistance coefficient, addressing the challenge of determining its value accurately. This model contributes to improving the prediction accuracy of the entry velocity of reservoir bank landslides, thereby enhancing risk assessment and mitigation efforts.
- physical model experiment /
- submerged landslide /
- landslide velocity calculation /
- water resistance coefficient /
- Baige landslide

HTML全文

滑坡的破坏性大小往往与其速度息息相关，美国华盛顿州Oso滑坡速度达到了1 m/s，造成43人死亡^[1]；意大利威尼斯Vaiont水坝滑坡以3 m/s的速度冲向大坝下游，1900余人在这场灾难中丧命^[2]；台湾小林滑坡时速达到83 m/s，埋葬了台湾南部整个小林村以及474名居民^[3]；1970年Huascaran滑坡以89 m/s的平均时速造成超过18000人死亡^[4]。这些事件表明更大滑坡速度具有更强的破坏性，因此对滑坡速度的准确计算对于其破坏性评估至关重要^[5]。

在滑坡速度计算中，一般来说考虑影响滑坡速度的因素包括滑坡岩土体性质、降雨^[6-7]以及滑动面摩擦系数的变化^[8]。WEN等^[9]发现每种类型的滑坡运动学参数与地质条件、地形状况与岩土工程特征具有较好的相关性。在水文学中降雨与河流水位变化都会引起滑坡体内孔隙水压力的变化，SCHULZ等^[10]发现滑坡加速与孔隙水压力增加相关。对于滑动面摩擦系数的研究，有助于了解滑坡启动中势能转化机制和滑动过程。SCHEIDEGGER^[11]探讨了滑面摩擦系数与滑坡体积之间的关系，将滑坡运动的阻力分解为一个常数和一个与速度相关的项。YAMADA等^[12]通过地震波形反演和数值模拟，将日本深部滑坡摩擦系数确定在0.3～0.4之间，质心处的最大速度为12～36 m/s。对于滑坡运动过程的分析，目前常用的数值模拟方法为光滑粒子流方法（SPH）^[13-14]、物质点法（MPM）^[15]等，可以较好地模拟滑坡的溃散过程。结合遥感影像与无人机倾斜摄影^[16]、滑坡发生时的地震动信号分析^[17]也可为滑坡的精准识别和运动过程分析提供参考。

库岸滑坡最重要的特征之一就是入水过程，库岸滑坡在入水过程中前缘受到水阻力会对其速度产生影响^[18-19]，代云霞等^[20]考虑了滑坡入水条块受水阻力的情况，对美国土木工程师协会推荐的滑速计算方法进行改进。而汪洋等^[21-22]则通过物理模型试验提出了水下运动试块迎水面的压强水头和阻力计算模型，并量化分析了水阻力对速度的影响。水阻力通常由受速度与物体表面形状控制的兴波阻力以及由水的粘性引起的粘压阻力组成。滑坡为不规则形状，并且高速运动的物体粘压阻力仅占水阻力的5%左右^[23]，所以滑坡水阻力的计算主要考虑兴波阻力。关于兴波阻力的计算主要的理论为Michell方法^[24]、Noblesse细长体理论^[25]、Dawson方法^[26-29]。

库岸滑坡在入水后其速度会发生显著变化。少数研究已考虑到入水过程中迎水面的阻力影响，但未分析水阻力对滑坡运动的整体作用，而滑坡在水中的受力情况与船舶存在较大差异，无法直接利用现有结论。本研究设计了试块入水阻力试验系统，构建了水阻力系数计算模型，基于模型无量纲化分析了试块入水速度、河道水深与滑体横截面积对水阻力系数的影响，提出了水阻力系数理论公式，并选取金沙江白格滑坡为实例，应用本研究提出的理论公式进行滑坡运动速度计算并与现有结果进行对比分析。

1. 物理模型试验

1.1 物理模型试验设计的理论依据

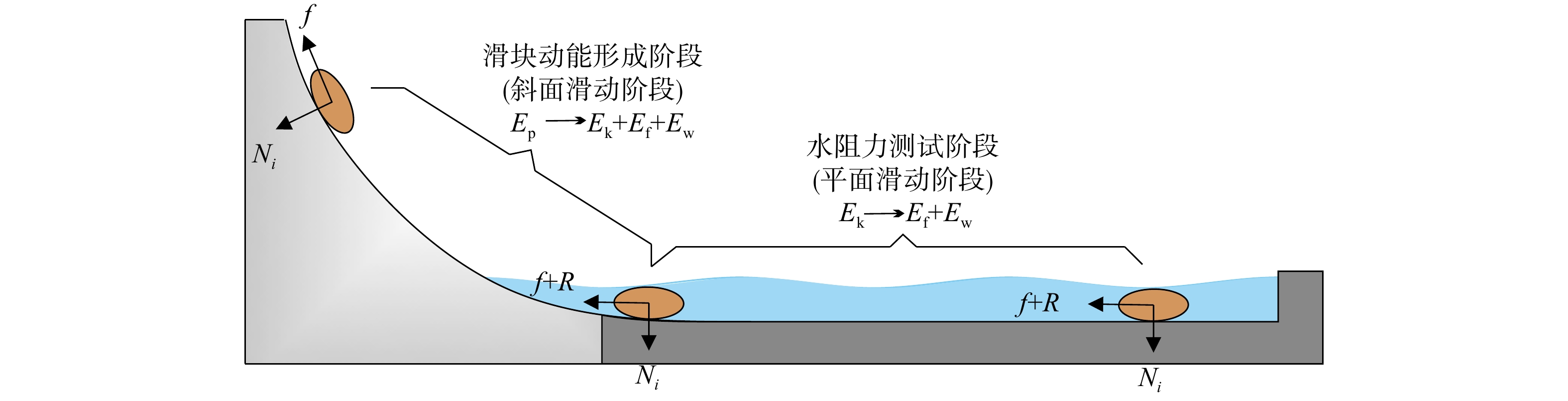
以试块入水运动过程的能量分析作为物理模型试验设计的理论依据，试块的入水运动过程分为斜面滑动阶段与平面滑动阶段（图1），在斜面滑动阶段，试块的势能E_p转化为动能E_k、摩擦热能E_f以及被水阻力所消耗的能量E_w；从斜面底端开始的平面滑动阶段，初始动能E_k被动摩擦阻力f与水阻力R完全消耗直至试块完全静止。取微小时间段dt， ${t}_{i}$ 到 ${t}_{i+1}$ 时刻经历的时间为dt，各时刻对应的速度分别为 ${v}_{i}$ 和 ${v}_{i+1}$ ，结合水阻力计算模型^[30-31]，该过程可表示为：

图 1 基于试验数据的水阻力系数计算模型

f. 动摩擦阻力；E_p. 势能；E_k. 动能；E_f. 摩擦热能；E_w. 被水阻力消耗的能量；R. 水阻力；N_i. 浮重度

Figure 1. Calculation model of the water resistance coefficient the basis of experimental data

下载: 全尺寸图片幻灯片

$\begin{aligned} \frac{1}{2}{m}_{{\mathrm{L}}}\left[{v}^{2}\left({t}_{\mathrm{i}}\right)-{v}^{2}\left({t}_{\mathrm{i}+1}\right)\right]&={N}_{i}\mu {\int }_{{t}_{i}}^{{t}_{i+1}}v\left(t\right){\mathrm{d}}t+\\ &\frac{1}{2}{{C}_{{\mathrm{w}}}\rho }_{{\mathrm{w}}}A{v}^{2}\left({t}_{i+1}\right){\int }_{{t}_{i}}^{{t}_{i+1}}v\left(t\right){\mathrm{d}}t， \end{aligned}$

(1)

式中： ${m}_{{\mathrm{L}}}$ 为试块质量； ${N}_{i}$ 为试块i在平面滑动阶段的浮重度，即正压力； $v\left(t\right)$ 为试块关于时间 $t$ 的速度函数； $\mu$ 为模拟河床动摩擦阻力系数； ${C}_{{\mathrm{w}}}$ 为水阻力系数； ${\rho }_{{\mathrm{w}}}$ 为水体密度； $A$ 为试块在运动方向上的正交投影面积。

动摩擦阻力系数 $\mu$ 与水阻力系数 ${C}_{{\mathrm{w}}}$ 是2个未知量，在斜面滑动阶段，试块与接触面间的正压力 ${N}_{i}$ 方向与大小不断变化，求解动摩擦阻力系数比较复杂。为了更精确获取动摩擦阻力系数，选取平面滑动阶段来分析获取数据；求解动摩擦阻力选取无水条件，且要确保平面段是湿润的。

1.2 试验方案设计

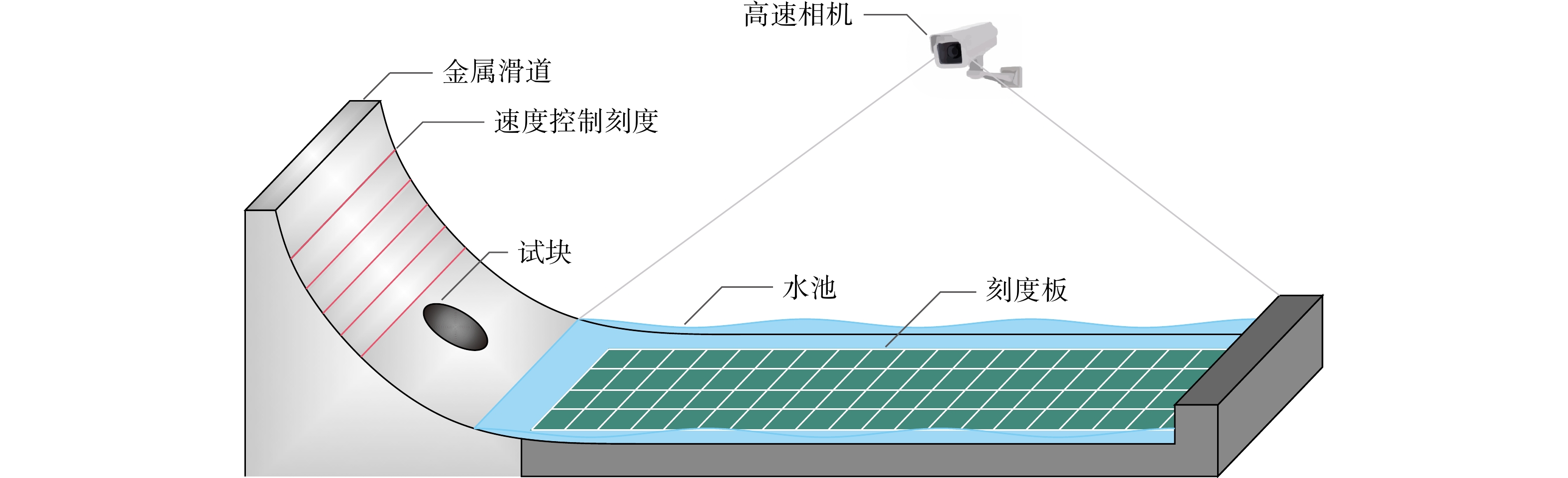
本试验为试块入水阻力试验，通过金属滑道、水池、试块组成的运动系统来模拟滑坡体的入水过程（图2）。测量系统由高速相机与刻度板组成，高速相机布置在运动系统的正右方与正上方，用于拍摄试块滑动到最低点后从入水到完全静止的平面滑动阶段。相机实时采集帧率为40.53，图像摄制速度为25 ms/张，通过试块运动视频背景中刻度版的网格（mm）可以读取试块的运动位置与轨迹。

图 2 物理模型试验系统示意图

Figure 2. Schematic diagram of the physical model test system

下载: 全尺寸图片幻灯片

在试验中选取滑体入水速度v、河道水深h、横截面积A作为试块入水阻力的影响因子。按表1试验工况设计，速度设置5种工况，通过将试块置于金属滑道上标记的速度1到速度5的速度控制刻度来控制（）；水深设置4种工况，通过水池水深控制；横截面积设置6种工况，通过测量选取不同横截面积的试块来控制。在试块的平面滑动阶段同时受到动摩擦阻力与水阻力，依据式（1），为确定摩擦阻力所消耗的能量，通过试块1～6（各试块参数见）无水工况试验确定河道动摩擦阻力系数 $\mu$ ； $\mu$ 值确定后，通过预试验选取入水运动姿态稳定的试块3～6，将选取的试块分别在速度5、水深3下进行入水阻力试验，来计算分析水阻力系数 ${C}_{{\mathrm{w}}}$ 。

表 1 试验工况

Table 1. Experimental Conditions

参数	水平	备注
滑体入水速度v/(cm·s⁻¹)	171(速度1)，151(速度2)， 131(速度3)，111(速度4)，91(速度5)	刻度与地面垂直高度
河道水深h/cm	无水工况：0	无水工况下地面为湿润状态
河道水深h/cm	有水工况：10(水深1)， 15(水深2)，20(水深3)	无水工况下地面为湿润状态
横截面面积A/cm²	7.7，9.5，30.3，33.8，42.0，48.9	—

下载: 导出CSV

| 显示表格

图 3 速度控制刻度 (a) 与试块 (b～g)

Figure 3. Speed control scale (a) and test block (b-g)

下载: 全尺寸图片幻灯片

表 2 试块参数

Table 2. Parameters of the test samples

试块	横截面面积A/cm²	试验室质量/g	ρ/(g·cm⁻³)	厚度/cm
试块1	7.7	73.4	2.8	2.4
试块2	9.5	118.1	2.7	3.1
试块3	30.3	506.1	2.7	3.6
试块4	33.8	663.0	2.6	4.6
试块5	42.0	1202.2	2.6	5.4
试块6	48.9	1027.7	2.7	6.2

下载: 导出CSV

| 显示表格

2. 水阻力系数分析

2.1 动摩擦阻力系数

在无水试验工况下，对试块与河道进行湿润处理，不考虑水对试块的浮力与水阻力，动摩擦阻力消耗的能量为其在位移中所做的功，由式（1）可得动摩擦阻力系数μ表达式：

$\begin{aligned} \mu =\frac{\left[{v}^{2}\left({t}_{i}\right)-{v}^{2}\left({t}_{i+1}\right)\right]}{2g{\int }_{{t}_{i}}^{{t}_{i+1}}v\left(t\right){\mathrm{d}}t}， \end{aligned}$

(2)

式中：g为重力加速度。

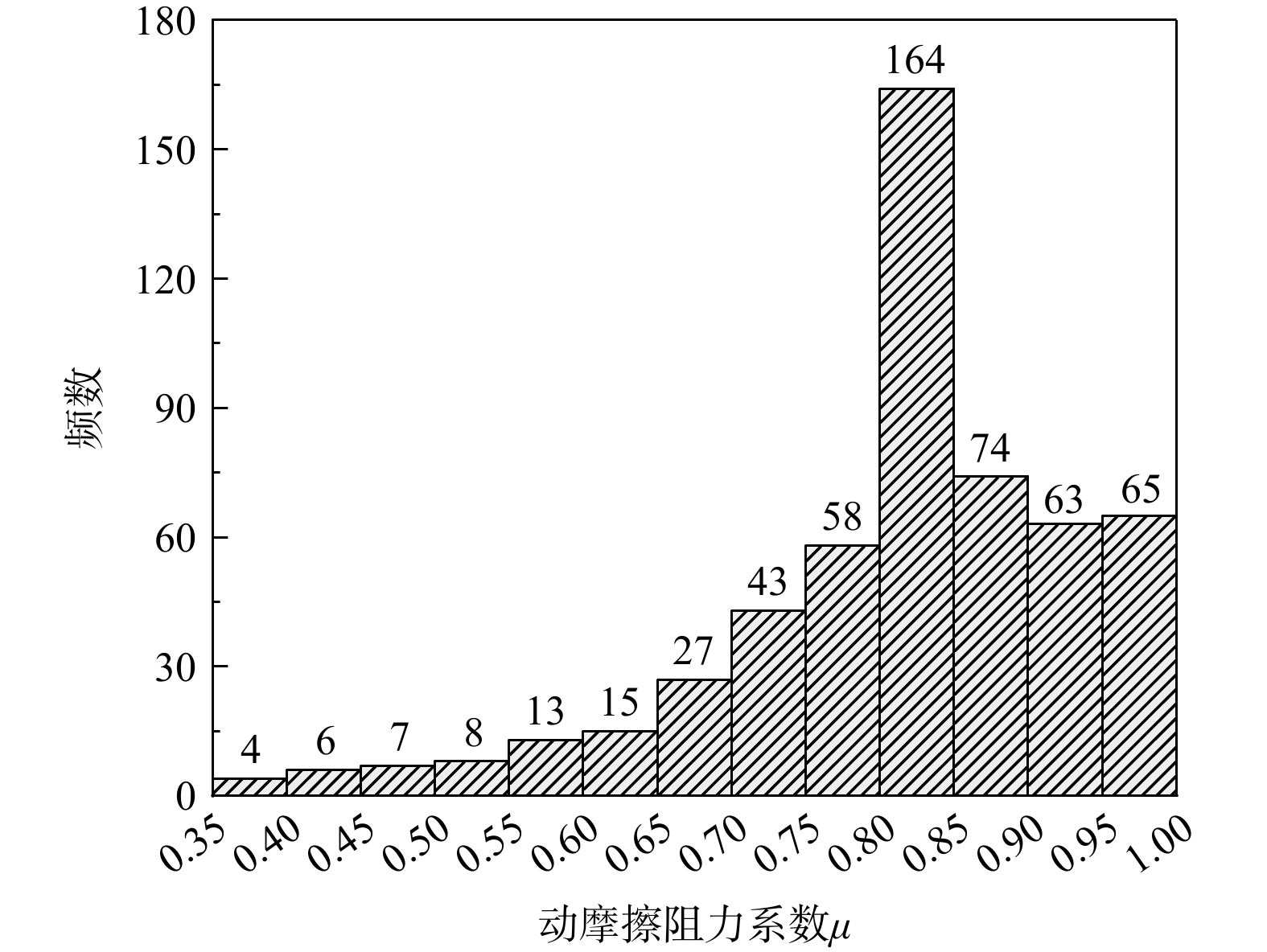
根据上式结合试验数据进行计算，统计各时刻动摩擦阻力系数，从各工况下动摩擦阻力系数的频数统计来看，85.4%动摩擦阻力系数计算值分布在0.75～1区间，其中30.0%集中分布在0.80～0.85区间，其区间均值为0.81（图4）。

图 4 动摩擦阻力系数频数统计

Figure 4. Frequency statistics of the dynamic friction coefficients

下载: 全尺寸图片幻灯片

2.2 水阻力系数模型

确定 $\mu$ 后，根据公式（1），水阻力系数计算模型计算如下：

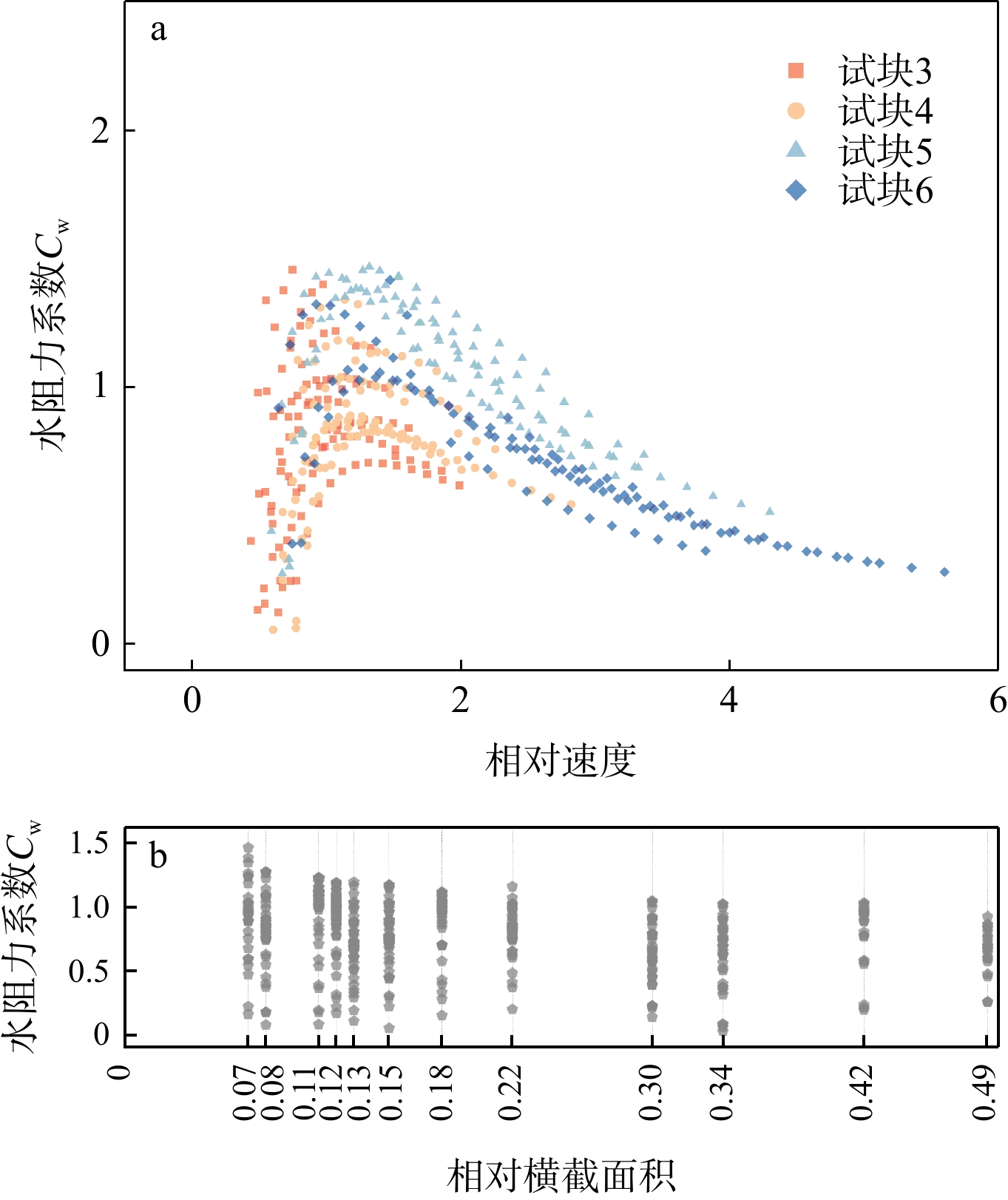
${C}_{{\mathrm{w}}}=\dfrac{\dfrac{1}{2}{m}_{{\mathrm{L}}}\left[{v}^{2}\left({t}_{{i}}\right)-{v}^{2}\left({t}_{{i}+1}\right)\right]-{N_{{i}}}\mu {\int }_{{t}_{i}}^{{t}_{i+1}}v\left(t\right){\mathrm{d}}t}{\dfrac{1}{2}{\rho }_{{\mathrm{w}}}A{v}^{2}\left({t}_{i+1}\right){\int }_{{t}_{i}}^{{t}_{i+1}}v\left(t\right){\mathrm{d}}t} 。$

(3)

为消除物理单位影响，采用无量纲分析方法研究入水速度v、河道水深h、横截面积A 3个参数对水阻力系数的影响。采用相对速度（弗劳德数） ${v}/{\sqrt{gh}}$ 、相对横截面积 ${A}/{{h}^{2}}$ 对水阻力系数进行计算分析。通过图5可以看出，随着相对速度增加，曲线整体呈现先上升后下降的趋势。相对速度在0～1.28区间时，随着相对速度增大，水阻力系数有增大的趋势，并且上升幅度较大，变化率为68.4%；相对速度在1.28～6区间时，水阻力系数下降幅度比较平缓，变化率为12.6%。各速度下试块横截面积改变时，随着相对横截面的增加，水阻力系数整体呈现减小的趋势。

图 5 水阻力系数与相对速度 (a)、相对横截面积 (b) 的相关关系

Figure 5. Hydrodynamic resistance coefficients correlation with relative velocity (a) and relevant cross-sectional area (b)

下载: 全尺寸图片幻灯片

为进一步量化水阻力系数，确定3个参数对水阻力系数的影响程度，通过无量纲多元线性回归分析，结合试验数据与公式（3），得到水阻力系数与3个参数的理论公式：

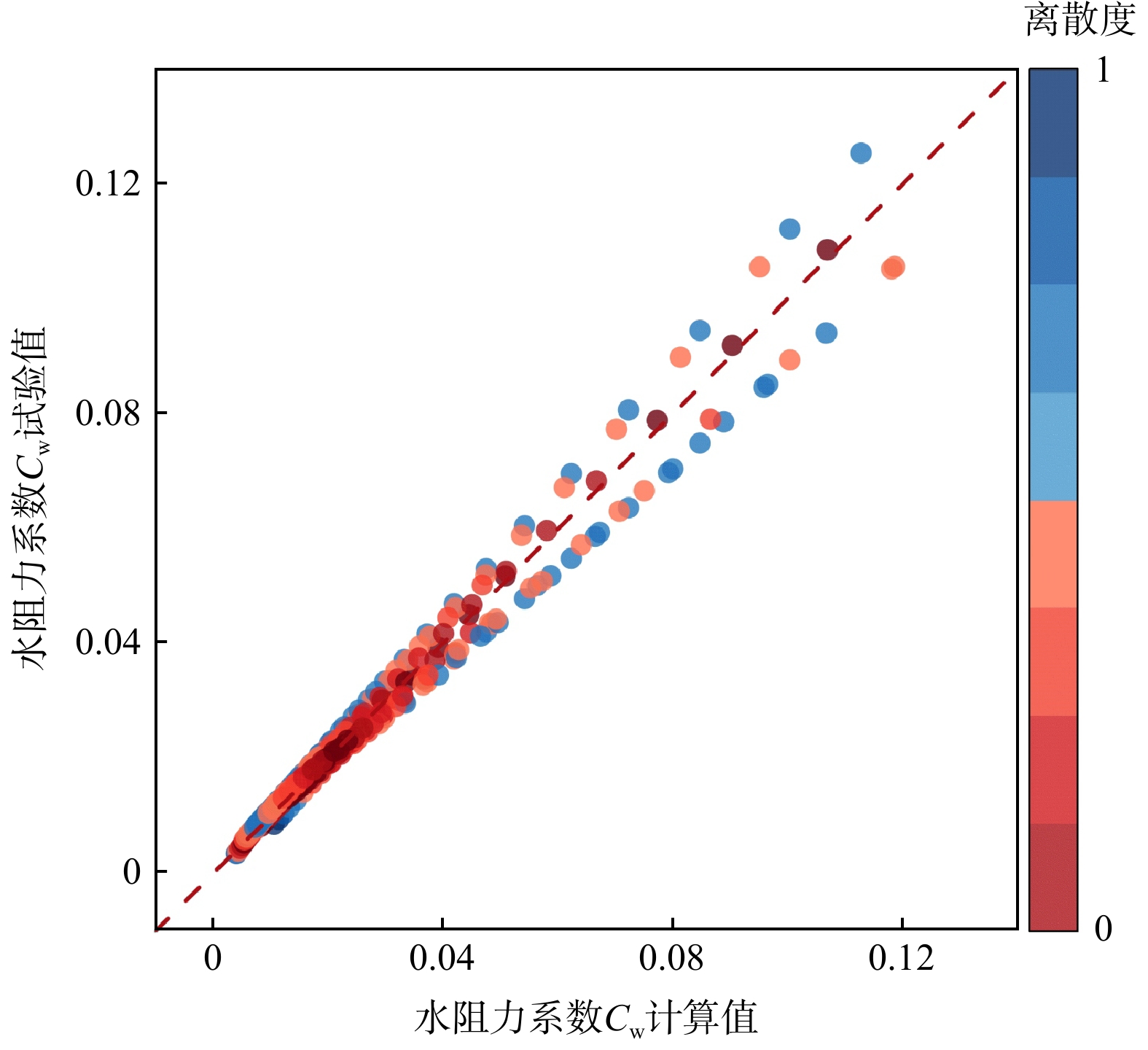
${C}_{{\mathrm{w}}}={a\left(\frac{v}{\sqrt{gh}}\right)}^{b}{\left(\frac{A}{{h}^{2}}\right)}^{c} 。$

(4)

通过对公式（4）进行非线性拟合，确定参数a=1.3，b=0.3，c=0.15，拟合度R²=0.77，表明理论公式具有较好准确度（图6）。

图 6 水阻力系数试验值与计算值比值

Figure 6. Ratio of experimental to calculated values of the water resistance coefficients

下载: 全尺寸图片幻灯片

3. 实例分析

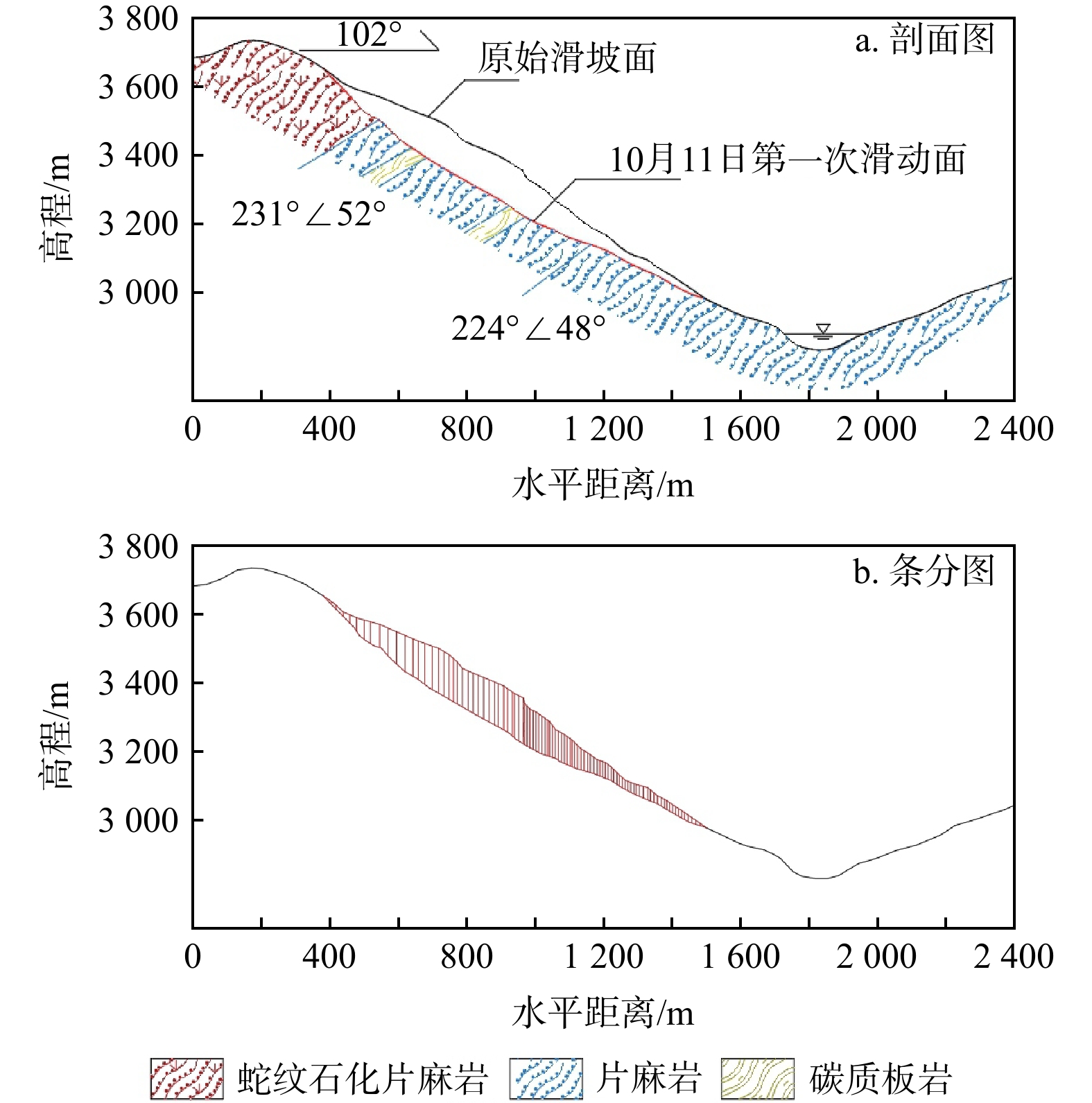
白格滑坡位于西藏自治区江达县白格村金沙江右岸，2018年10月11日和2018年11月3日先后发生2次滑坡^[32]。滑坡第1次滑动为整体迅速启动，势能转化为动能，高速滑跃冲入金沙江；第2次滑动位于第1次滑动的后缘，为局部垮塌^[33]。第1次滑坡体积约为3100×10⁴ m³，宽约645 m，长约1265 m，厚约150.6 m，前缘和后缘高程分别为2981 m和3723 m，坡度50°～65°^[34]（图7，8a），滑坡区出露地层主要为元古宙雄松群浅灰−深灰色片麻岩和零星出露的灰绿色蛇纹岩地层，岩层产状为231°∠52°，属于倾内斜向斜坡。受区域构造作用、地下水升降以及风化作用等因素影响，岩体节理裂隙极为发育，岩体结构破碎，主要发育2组节理，产状分别为65°∠56°，120°∠37°^[33]。

图 7 白格滑坡遥感图

Figure 7. Remote sensing image of the Baige landslide

下载: 全尺寸图片幻灯片

图 8 白格滑坡剖面图 (a) 与条分图 (b)

Figure 8. Cross-sectional profile (a) and strip map (b) of the Baige landslide

下载: 全尺寸图片幻灯片

滑坡滑动过程中滑带黏聚力为13.05 kPa，滑带天然内摩擦角为32.6°，饱和内摩擦角为30.9°^[35]。为考虑通过水阻力系数修正后的水阻力对滑坡运动速度的影响，选取白格滑坡10月11日第1次滑坡进行计算，与现有结果^[32-33]进行对比分析（图8b）。计算采用条分法，假定各条块为刚体，库岸滑坡运动受到的水阻力增量的方向沿滑坡运动方向，认为前一条块和后一条块作用于当前条块的合力方向与滑面平行；认为同一时刻，所有条块具有相同的加速度，计算结果为滑坡的质心速度，根据运动学方程^[21]：

${v}_{i}^{2}={v}_{i-1}^{2}+2{a}_{i}{l}_{i}，$

(5)

式中： ${v}_{i}$ 为条块 $i$ 的速度； ${a}_{i}$ 为条块i的加速度； ${l}_{i}$ 为条块 $i$ 滑动面的长度。

在考虑水阻力系数模型的情况下：

${a}_{i}=\frac{\displaystyle\sum _{i=1}^{n} {W}_{i}{\phi}_{1i}+\displaystyle\sum _{i=1}^{n} {P}_{i}{\phi}_{2i}-\displaystyle\sum _{i=1}^{n} {c}_{i}{l}_{i}-\displaystyle\sum _{i=1}^{n} \dfrac{1}{2}{{C}_{{\mathrm{w}}}\rho }_{{\mathrm{w}}}A{v}^{2}\left({t}_{i+1}\right)}{\displaystyle\sum _{i=1}^{n} {m}_{i}}，$

(6)

式中： ${W}_{i}$ 为条块 $i$ 的重量； ${P}_{i}$ 为渗透力； ${c}_{i}$ 为滑面内聚力； ${m}_{i}$ 为质量，其中：

$\left\{\begin{array}{c}{\phi }_{1i}={\mathrm{sin}}{\alpha }_{i}-{\mathrm{cos}}{\alpha }_{i}{\mathrm{tan}}{\phi }_{i}\\ {\phi }_{2i}={\mathrm{cos}}({\theta }_{i}-{\alpha }_{i})-{\mathrm{sin}}({\theta }_{i}-{\alpha }_{i}){\mathrm{tan}}{\phi }_{i}\end{array}\right. ，$

(7)

式中： ${\phi }_{1i}$ ， ${\phi }_{2i}$ 为中间变量； ${\alpha }_{i}$ 为滑面倾角； ${\theta }_{i}$ 为地下水浸润线倾角； ${\phi }_{i}$ 为内摩擦角。

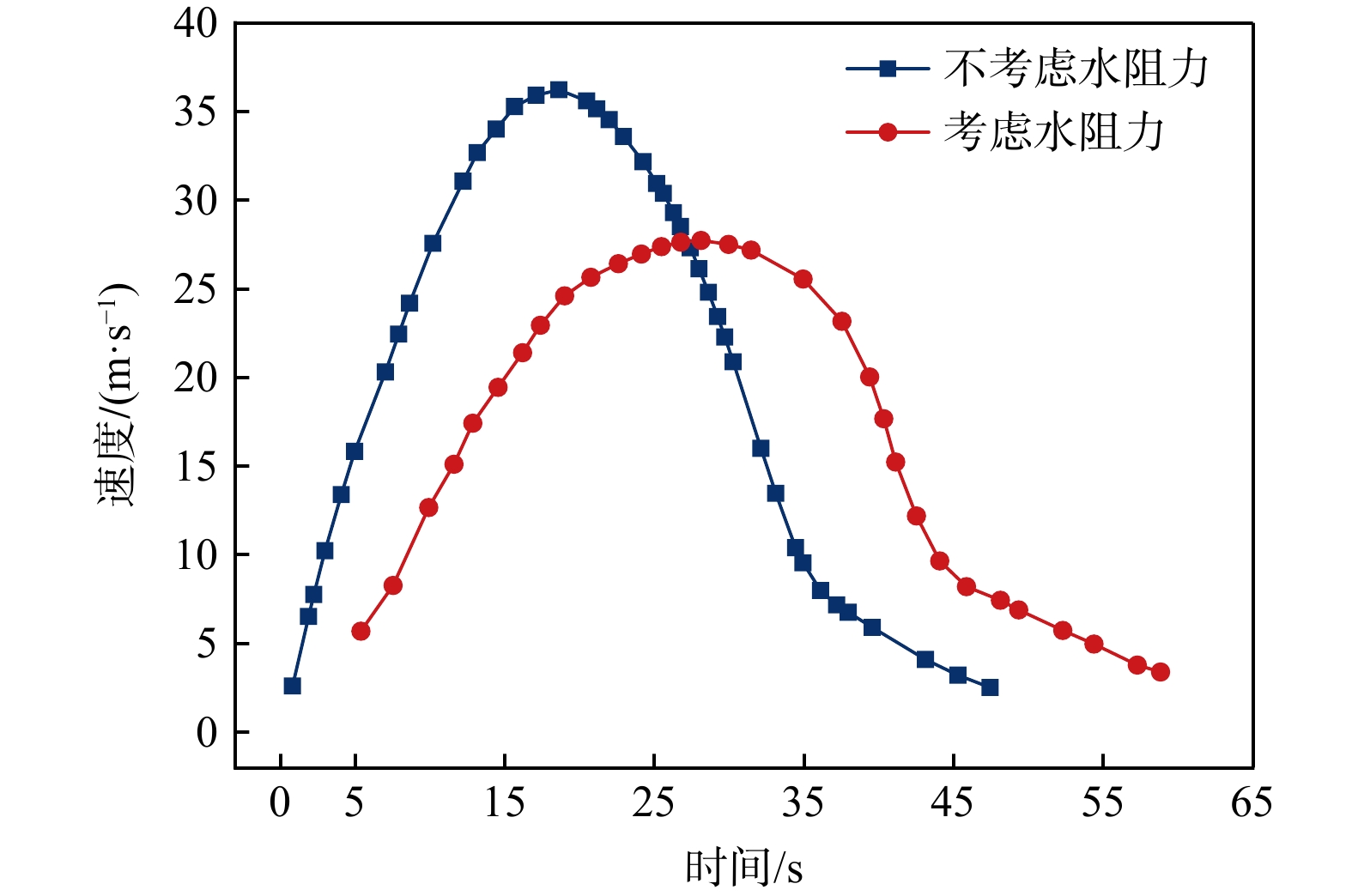
在不考虑水阻力的情况下，滑坡运动的最大速度为36.2 m/s，达到最大运动速度的时刻为18.6 s；在考虑水阻力的情况下，滑坡运动的最大速度为27.7 m/s，达到最大运动速度的时刻为26.3 s。2种情况下最大速度差值为8.5 m/s，相较于不考虑水阻力的情况，考虑水阻力的情况下，其最大运动速度减小了23.5%，最大速度时刻延后了7.7 s（图9），表明水阻力对滑坡的下滑过程存在一定程度的影响，因此对库岸滑坡运动过程的准确计算需要考虑系数修正后的水阻力作用。

图 9 白格滑坡运动速度

Figure 9. Movement velocity of the Baige landslide

下载: 全尺寸图片幻灯片

4. 结　论

（1）基于试块的入水运动过程分析，结合能量守恒定律，设计并进行了滑坡入水阻力模型试验。在无水工况下进行了6个试块对照试验来确定模拟河道的动摩擦力系数；在有水工况下基于对速度、水深、横截面积3个变量的考虑进行了4个试块在5个速度工况和3个水深工况的入水阻力试验。

（2）统计分析了动摩擦阻力系数频数分布，其中30.0%集中分布在0.80～0.85区段，其区间均值为0.81；提出了基于试验数据的水阻力系数计算模型，采用无量纲化分析方法，分析了各无量纲因子对水阻力系数的影响，随着相对速度的增加，水阻力系数整体呈现先上升后下降的趋势；随着相对横截面积增加，水阻力系数减小。通过无量纲多元线性回归分析得出了水阻力系数的理论公式，且理论公式具有较好的拟合度，R²=0.77。

（3）结合水阻力计算模型，开展了白格滑坡速度计算，与白格滑坡现有结果进行对比，结果表明最大速度差值为8.5 m/s，在考虑水阻力系数的情况下最大运动速度减小了23.5%，最大速度时刻延后了7.7 s。

为了更精确地测定水阻力相关的参数，本研究选取刚体来开展试验，相较于实际情况存在一定的局限性和不足，不能考虑滑坡失稳入水运动过程中岩土体的溃散现象，后期研究将通过数值模拟来开展这方面的研究。

所有作者声明不存在利益冲突。

The authors declare that no competing interests exist.

图 1 基于试验数据的水阻力系数计算模型

f. 动摩擦阻力；E_p. 势能；E_k. 动能；E_f. 摩擦热能；E_w. 被水阻力消耗的能量；R. 水阻力；N_i. 浮重度

Figure 1. Calculation model of the water resistance coefficient the basis of experimental data

下载: 全尺寸图片幻灯片

图 2 物理模型试验系统示意图

Figure 2. Schematic diagram of the physical model test system

下载: 全尺寸图片幻灯片

图 3 速度控制刻度 (a) 与试块 (b～g)

Figure 3. Speed control scale (a) and test block (b-g)

下载: 全尺寸图片幻灯片

图 4 动摩擦阻力系数频数统计

Figure 4. Frequency statistics of the dynamic friction coefficients

下载: 全尺寸图片幻灯片

图 5 水阻力系数与相对速度 (a)、相对横截面积 (b) 的相关关系

Figure 5. Hydrodynamic resistance coefficients correlation with relative velocity (a) and relevant cross-sectional area (b)

下载: 全尺寸图片幻灯片

图 6 水阻力系数试验值与计算值比值

Figure 6. Ratio of experimental to calculated values of the water resistance coefficients

下载: 全尺寸图片幻灯片

图 7 白格滑坡遥感图

Figure 7. Remote sensing image of the Baige landslide

下载: 全尺寸图片幻灯片

图 8 白格滑坡剖面图 (a) 与条分图 (b)

Figure 8. Cross-sectional profile (a) and strip map (b) of the Baige landslide

下载: 全尺寸图片幻灯片

图 9 白格滑坡运动速度

Figure 9. Movement velocity of the Baige landslide

下载: 全尺寸图片幻灯片

表 1 试验工况

Table 1. Experimental Conditions

参数	水平	备注
滑体入水速度v/(cm·s⁻¹)	171(速度1)，151(速度2)， 131(速度3)，111(速度4)，91(速度5)	刻度与地面垂直高度
河道水深h/cm	无水工况：0	无水工况下地面为湿润状态
河道水深h/cm	有水工况：10(水深1)， 15(水深2)，20(水深3)	无水工况下地面为湿润状态
横截面面积A/cm²	7.7，9.5，30.3，33.8，42.0，48.9	—

下载: 导出CSV

表 2 试块参数

Table 2. Parameters of the test samples

试块	横截面面积A/cm²	试验室质量/g	ρ/(g·cm⁻³)	厚度/cm
试块1	7.7	73.4	2.8	2.4
试块2	9.5	118.1	2.7	3.1
试块3	30.3	506.1	2.7	3.6
试块4	33.8	663.0	2.6	4.6
试块5	42.0	1202.2	2.6	5.4
试块6	48.9	1027.7	2.7	6.2

下载: 导出CSV

参考文献(35)

[1]	COLLINS B D,REID M E. Enhanced landslide mobility by basal liquefaction:The 2014 State Route 530 (Oso),Washington,landslide[J]. Geological Society of America Bulletin,2020,132(3/4):451-476.
[2]	SITAR N,MACLAUGHLIN M M,DOOLIN D M. Influence of kinematics on landslide mobility and failure mode[J]. Journal of Geotechnical and Geoenvironmental Engineering,2005,131(6):716-728. doi: 10.1061/(ASCE)1090-0241(2005)131:6(716)
[3]	LIN C H. Insight into landslide kinematics from a broadband seismic network[J]. Earth,Planets and Space,2015,67(1):8.
[4]	SCHUSTER R L,FLEMING R W. Economic losses and fatalities due to landslides[J]. Environmental & Engineering Geoscience,1986,xxiii(1):11-28.
[5]	廖德武,郑冰,杜艳松,等. 兴仁“6·10” 彭家洞高速滑坡运动特征与形成机理[J]. 地质科技通报,2022,41(6):66-76. LIAO D W,ZHENG B,DU Y S,et al. Movement characteristics and formation mechanism of the “6·10” Pengjiadong high speed landslide in Xingren[J]. Bulletin of Geological Science and Technology,2022,41(6):66-76. (in Chinese with English abstract
[6]	许艺林,李远耀,李思德,等. 库水位下降叠加降雨作用时堆积层滑坡渗流−变形机制[J]. 地质科技通报,2024,43(1):216-228. XU Y L,LI Y Y,LI S D,et al. Seepage-deformation mechanism of colluvial landslides under the action of reservoir water level decline and rainfall[J]. Bulletin of Geological Science and Technology,2024,43(1):216-228. (in Chinese with English abstract
[7]	谢洋义,殷坤龙,杜娟,等. 基于不同地质环境分区的重庆市滑坡降雨阈值模型研究[J]. 地质科技通报,2025,44(1):126-137. XIE Y Y,YIN K L,DU J,et al. Threshold model of landslide rainfall in Chongqing based on different geological environment zones[J]. Bulletin of Geological Science and Technology,2025,44(1):126-137. (in Chinese with English abstract
[8]	张抒,唐辉明,龚文平,等. 基于物理力学机制的滑坡数值预报模式:综述、挑战与机遇[J]. 地质科技通报,2022,41(6):14-27. ZHANG S,TANG H M,GONG W P,et al. Landslide numerical forecasting mode based on physical- mechanical mechanism:Overviews,challenges and opportunities[J]. Bulletin of Geological Science and Technology,2022,41(6):14-27. (in Chinese with English abstract
[9]	WEN B P,WANG S J,WANG E Z,et al. Characteristics of rapid giant landslides in China[J]. Landslides,2004,1(4):247-261. doi: 10.1007/s10346-004-0022-4
[10]	SCHULZ W H,MCKENNA J P,KIBLER J D,et al. Relations between hydrology and velocity of a continuously moving landslide:Evidence of pore-pressure feedback regulating landslide motion?[J]. Landslides,2009,6(3):181-190. doi: 10.1007/s10346-009-0157-4
[11]	SCHEIDEGGER A E. On the prediction of the reach and velocity of catastrophic landslides[J]. Rock Mechanics,1973,5(4):231-236. doi: 10.1007/BF01301796
[12]	YAMADA M,MANGENEY A,MATSUSHI Y,et al. Estimation of dynamic friction and movement history of large landslides[J]. Landslides,2018,15(10):1963-1974. doi: 10.1007/s10346-018-1002-4
[13]	唐岳灏,姜清辉. SPH-DEM流固耦合方法模拟金沙江白格滑坡应用研究[J]. 长江工程职业技术学院学报,2023,40(2):1-8. TANG Y H,JIANG Q H. Study on application of SPH-DEM fluid-structure interaction to simulating baige landslide in Jinsha River[J]. Journal of Changjiang Institute of Technology,2023,40(2):1-8. (in Chinese with English abstract
[14]	唐岳灏,姜清辉. 金沙江白格滑坡残留体稳定性及堵江风险分析[J]. 水利水电快报,2023,44(5):38-44. TANG Y H,JIANG Q H. Stability and risk assessment of the residual body landslide and river blockage in Baige,Jinsha River[J]. Express Water Resources & Hydropower Information,2023,44(5):38-44. (in Chinese with English abstract
[15]	钟启明,吴昊,单熠博,等. 基于物质点法的白格滑坡堰塞坝形成过程数值模拟[J]. 人民长江,2024,55(4):25-31. ZHONG Q M,WU H,SHAN Y B,et al. Numerical simulation of Baige landslide barrier dam formation process based on material point method[J]. Yangtze River,2024,55(4):25-31. (in Chinese with English abstract
[16]	杨云建,周学铖,何中海,等. 多时相数字孪生滑坡变形监测方法与应用研究:以金沙江白格滑坡为例[J]. 水文地质工程地质,2024,51(2):132-143. YANG Y J,ZHOU X C,HE Z H,et al. Multi-temporal digital twin method and application of landslide deformation monitoring:A case study on Baige landslide in Jinsha River[J]. Hydrogeology & Engineering Geology,2024,51(2):132-143. (in Chinese with English abstract
[17]	林子钰,范刚,陈骎,等. 基于地震动信号分析的滑坡堵江过程研究:以白格滑坡堰塞湖为例[J]. 人民长江,2023,54(10):90-97. LIN Z Y,FAN G,CHEN Q,et al. Study on landslide blocking process based on ground motion signals analysis:Case of Baige landslide dammed lake[J]. Yangtze River,2023,54(10):90-97. (in Chinese with English abstract
[18]	殷坤龙,张宇,汪洋. 水库滑坡涌浪风险研究现状和灾害链风险管控实践[J]. 地质科技通报,2022,41(2):1-12. YIN K L,ZHANG Y,WANG Y. A review of landslide-generated waves risk and practice of management of hazard chain risk from reservoir landslide[J]. Bulletin of Geological Science and Technology,2022,41(2):1-12. (in Chinese with English abstract
[19]	胡大儒,吴述彧,罗超鹏,等. 澜沧江某巨型堆积体蓄水失稳诱发涌浪预测[J]. 地质科技通报,2024,43(6):78-88. HU D R,WU S Y,LUO C P,et al. Prediction of the wave induced by a gaint accumulation impoundment instability in Lantsang River[J]. Bulletin of Geological Science and Technology,2024,43(6):78-88. (in Chinese with English abstract
[20]	代云霞,殷坤龙,汪洋. 滑坡速度计算及涌浪预测方法探讨[J]. 岩土力学,2008,29(增刊1):407-411. DAI Y X,YIN K L,WANG Y. Discussion on method of landslide velocity calculation and surge prediction[J]. Rock and Soil Mechanics,2008,29(S1):407-411. (in Chinese with English abstract
[21]	汪洋,殷坤龙,刘艺梁,等. 考虑水阻力的库岸滑坡运动速度计算模型研究[J]. 工程地质学报,2012,20(6):903-908. WANG Y,YIN K L,LIU Y L,et al. Model test speed model of fording landslide taking into account water resistance[J]. Journal of Engineering Geology,2012,20(6):903-908. (in Chinese with English abstract
[22]	汪洋,刘艺梁. 平面滑动型涉水岩质滑坡速度计算模型研究[J]. 灾害学,2012,27(3):22-24. WANG Y,LIU Y L. Study on speed model of fording rock landslide moving along the planar slip surface[J]. Journal of Catastrophology,2012,27(3):22-24. (in Chinese with English abstract
[23]	倪崇本. 基于CFD的船舶阻力性能综合研究[D]. 上海:上海交通大学,2011. NI C B. A comprehensive investigation of ship resistance prediction based on CFD theory[D]. Shanghai:Shanghai Jiaotong University,2011. (in Chinese with English abstract
[24]	BAŠIĆ J,BLAGOJEVIĆ B,ANDRUN M. Improved estimation of ship wave-making resistance[J]. Ocean Engineering,2020,200:107079. doi: 10.1016/j.oceaneng.2020.107079
[25]	吴广怀,吴培德,蒋耀军,等. 基于兴波阻力的三体船片体位置快速优化方法[J]. 船舶力学,2005,9(4):1-8. doi: 10.3969/j.issn.1007-7294.2005.04.001 WU G H,WU P D,JIANG Y J,et al. Fast method of positional optimization on distance between hulls of a trimaran based on wave resistance[J]. Journal of Ship Mechanics,2005,9(4):1-8. (in Chinese with English abstract doi: 10.3969/j.issn.1007-7294.2005.04.001
[26]	LI M X,CHEN Y,YUAN Z M,et al. Interference effects on the upstream wave generated by the catamaran moving across a depth change[J]. Ocean Engineering,2023,287:115939.
[27]	PENG H,NI S Y,QIU W. Wave pattern and resistance prediction for ships of full form[J]. Ocean Engineering,2014,87:162-173. doi: 10.1016/j.oceaneng.2014.06.004
[28]	卢晓平,王中,孙永华,等. Rankine源Dawson型方法求解三体船兴波阻力[J]. 华中科技大学学报(自然科学版),2008,36(11):103-107. doi: 10.3321/j.issn:1671-4512.2008.11.027 LU X P,WANG Z,SUN Y H,et al. Solution to wave resistance to trimanan using-Rankine source method of Dawson type[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition),2008,36(11):103-107. (in Chinese with English abstract doi: 10.3321/j.issn:1671-4512.2008.11.027
[29]	陈京普,朱德祥,刘晓东. 兴波阻力数值预报方法研究及其在集装箱船船型优化中的应用[J]. 水动力学研究与进展(A辑),2006,21(1):113-121. CHEN J P,ZHU D X,LIU X D. A research on numerical prediction method for wave-making resistance and its application to container ship hull form optimization[J]. Journal of Hydrodynamics (Ser A),2006,21(1):113-121. (in Chinese with English abstract
[30]	LIU S,HE G H,WANG Z K,et al. Resistance and flow field of a submarine in a density stratified fluid[J]. Ocean Engineering,2020,217:107934. doi: 10.1016/j.oceaneng.2020.107934
[31]	ZENG Q S,HEKKENBERG R,THILL C,et al. Scale effects on the wave-making resistance of ships sailing in shallow water[J]. Ocean Engineering,2020,212:107654. doi: 10.1016/j.oceaneng.2020.107654
[32]	周礼,范宣梅,许强,等. 金沙江白格滑坡运动过程特征数值模拟与危险性预测研究[J]. 工程地质学报,2019,27(6):1395-1404. ZHOU L,FAN X M,XU Q,et al. Numerical simulation and hazard prediction on movement process characteristics of Baige landslide in Jinsha River[J]. Journal of Engineering Geology,2019,27(6):1395-1404. (in Chinese with English abstract
[33]	冯文凯,张国强,白慧林,等. 金沙江“10·11” 白格特大型滑坡形成机制及发展趋势初步分析[J]. 工程地质学报,2019,27(2):415-425. FENG W K,ZHANG G Q,BAI H L,et al. A preliminary analysis of the formation mechanism and development tendency of the huge Baige landslide in Jinsha River on October 11,2018[J]. Journal of Engineering Geology,2019,27(2):415-425. (in Chinese with English abstract
[34]	崔玉龙,许冲,焦其松,等. 金沙江白格两次滑坡几何形态分析与体积计算[J]. 工程地质学报,2019,27(增刊1):269-275. CUI Y L,XU C,JIAO Q S,et al. Geometric shape analysis and volume calculation of the two successive Baige landslides in Jinsha River[J]. Journal of Engineering Geology,2019,27(S1):269-275. (in Chinese with English abstract
[35]	杨仲康,魏进兵,高云建,等. 金沙江白格滑坡裂缝区失稳概率分析[J]. 工程科学与技术,2020,52(6):95-101. YANG Z K,WEI J B,GAO Y J,et al. Instability probability analysis of the cracking zones at the site of the Baige landslide in Jinsha River[J]. Advanced Engineering Sciences,2020,52(6):95-101. (in Chinese with English abstract

施引文献

资源附件(0)

访问统计

点击查看大图

图(9) / 表(2)

计量

文章访问数: 40
PDF下载量: 1
被引次数: 0

1. 物理模型试验
1.1 物理模型试验设计的理论依据
1.2 试验方案设计
2. 水阻力系数分析
2.1 动摩擦阻力系数
2.2 水阻力系数模型
3. 实例分析
4. 结　论

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

基于物理模型试验的库岸滑坡水阻力系数研究

doi: 10.19509/j.cnki.dzkq.tb20240247

作者简介:
谢云轩：E-mail：761194047@qq.com

通讯作者:
E-mail：wangyangcug@126.com

计量

Water resistance coefficient of bank slope landslides via physical model experiments

Author Bio:
E-mail：761194047@qq.com

Corresponding author: E-mail：wangyangcug@126.com

1. 物理模型试验

1.1 物理模型试验设计的理论依据

1.2 试验方案设计

2. 水阻力系数分析

2.1 动摩擦阻力系数

2.2 水阻力系数模型

3. 实例分析

4. 结　论

计量

目录

1. 物理模型试验

1.1 物理模型试验设计的理论依据

1.2 试验方案设计

2. 水阻力系数分析

2.1 动摩擦阻力系数

2.2 水阻力系数模型

3. 实例分析

4. 结　论

留言板

基于物理模型试验的库岸滑坡水阻力系数研究

doi: 10.19509/j.cnki.dzkq.tb20240247

作者简介: 谢云轩：E-mail：761194047@qq.com

通讯作者: E-mail：wangyangcug@126.com

计量

出版历程

Water resistance coefficient of bank slope landslides via physical model experiments

Author Bio: E-mail：761194047@qq.com

Corresponding author: E-mail：wangyangcug@126.com

1. 物理模型试验

1.1 物理模型试验设计的理论依据

1.2 试验方案设计

2. 水阻力系数分析

2.1 动摩擦阻力系数

2.2 水阻力系数模型

3. 实例分析

4. 结 论

计量

出版历程

目录

1. 物理模型试验

1.1 物理模型试验设计的理论依据

1.2 试验方案设计

2. 水阻力系数分析

2.1 动摩擦阻力系数

2.2 水阻力系数模型

3. 实例分析

4. 结 论

作者简介:
谢云轩：E-mail：761194047@qq.com

通讯作者:
E-mail：wangyangcug@126.com

Author Bio:
E-mail：761194047@qq.com

4. 结　论

4. 结　论