Elastoplastic analysis of rock and soil masses based on smooth finite element method
-
摘要:
随着大型工程项目的日益增多，工程中的岩土极限问题也频繁出现，致使采用数值方法处理时，经常面对极端的模型变形问题。传统有限元法在处理极端的模型变形，特别是采用低阶单元分析时，往往会产生收敛问题、体积锁定问题以及网格严重畸变而导致的应力失准问题。寻找一种新的方法进行数值分析具有重要意义。光滑有限元法是一种有效改进传统有限元法固有缺陷，提高求解精度和收敛速度的算法。基于光滑有限元法，结合一种修正的Mohr-Coulomb屈服准则和线性搜索优化算法，建立了岩土体弹塑性计算模型。最后，针对经典的条形基础承载力模型和边坡模型进行验算，数值计算结果与参考解均吻合较好。结果表明光滑有限元法的计算精度明显优于传统有限元法，验证了本研究算法的可行性和实用性。本研究采用光滑有限元法建立的计算模型进一步提高了岩土体弹塑性问题的计算精度，降低了采用传统有限元法分析时存在的计算误差及网格畸变引起的应力失准问题。
-
关键词:
- 光滑有限元法 /
- 弹塑性 /
- 岩土体 /
- 修正Mohr-Coulomb屈服准则 /
- 线性搜索
Abstract:Objective With the increasing number of large engineering projects, geotechnical limit problems are becoming more common, often leading to extreme model deformation when numerical methods are employed. The traditional finite element method frequently encounters convergence issues, volume locking, and stress misalignment due to severe mesh distortion during the analysis of extreme model deformation, especially when low-order elements are used. Therefore, developing a new method for numerical analysis is of great importance.
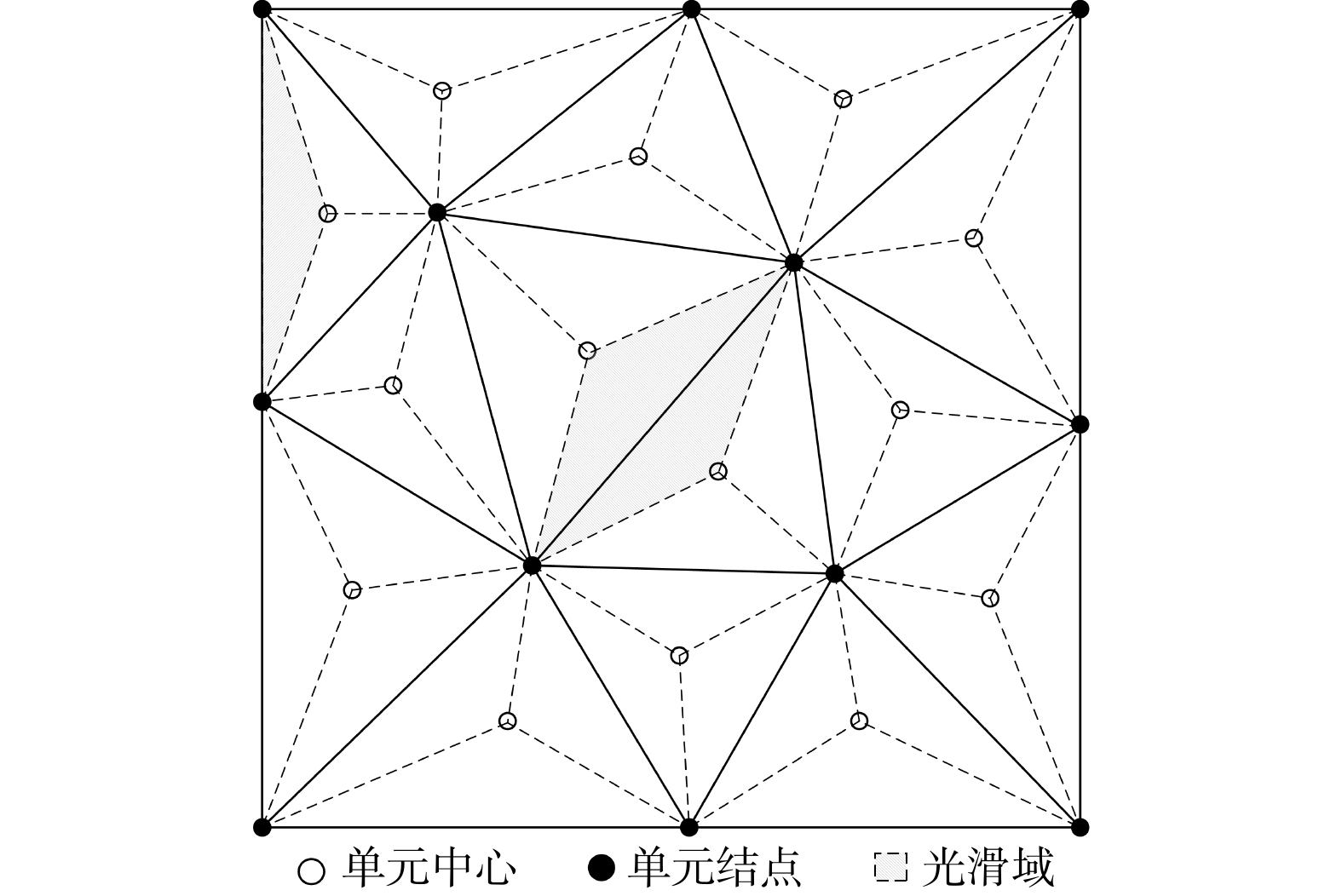
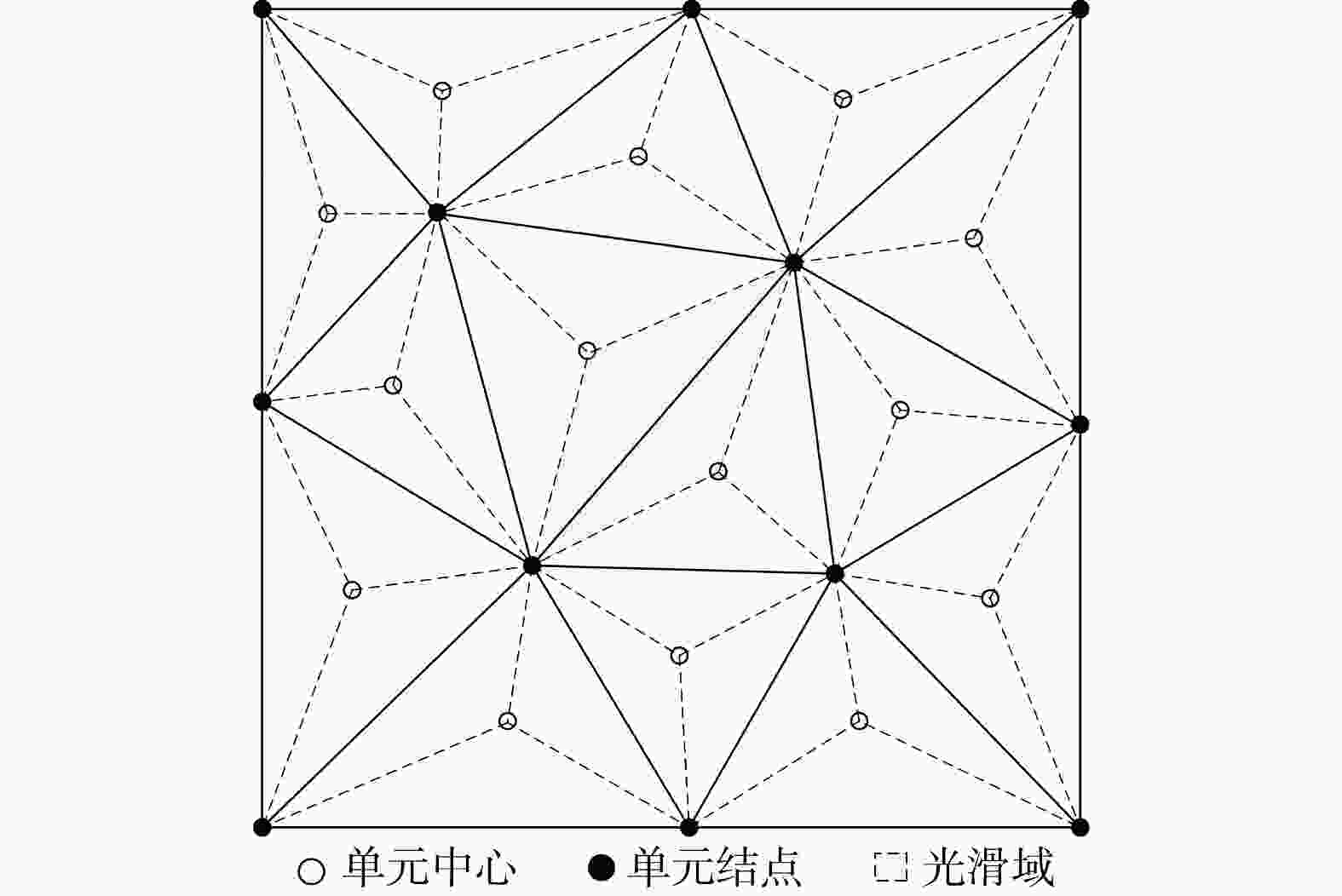
Methods The smooth finite element method is an effective approach to address the inherent defects of the traditional finite element method, enhancing both solution accuracy and convergence speed. Thus, based on the smooth finite element method combined with a modified Mohr-Coulomb yield criterion and a linear search optimization algorithm, an elastoplastic calculation model for rock and soil masses is developed in this study.
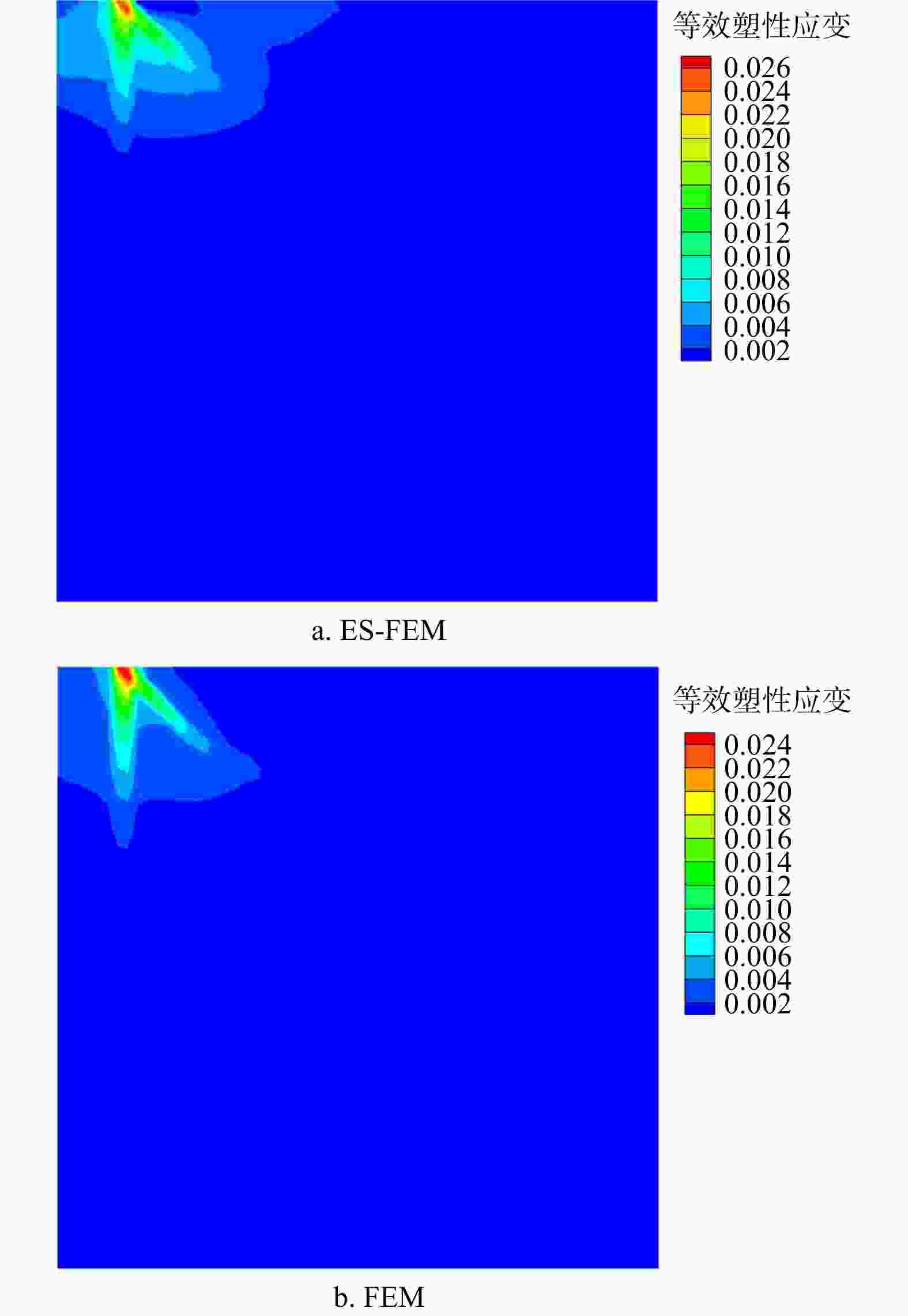
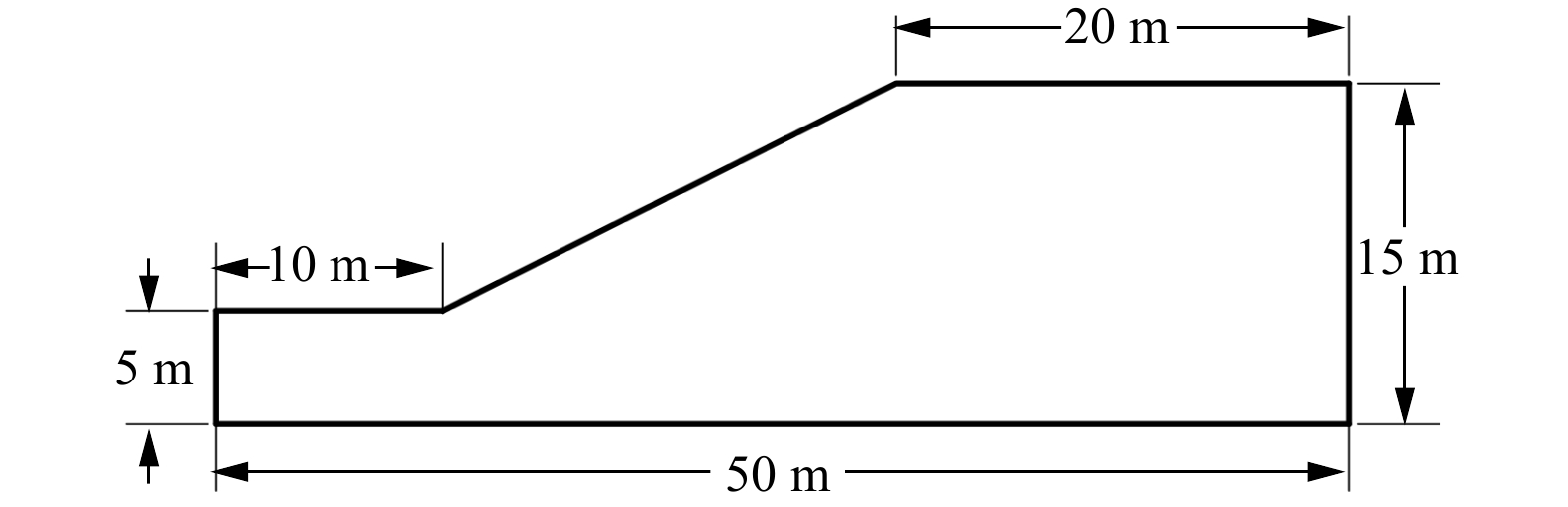
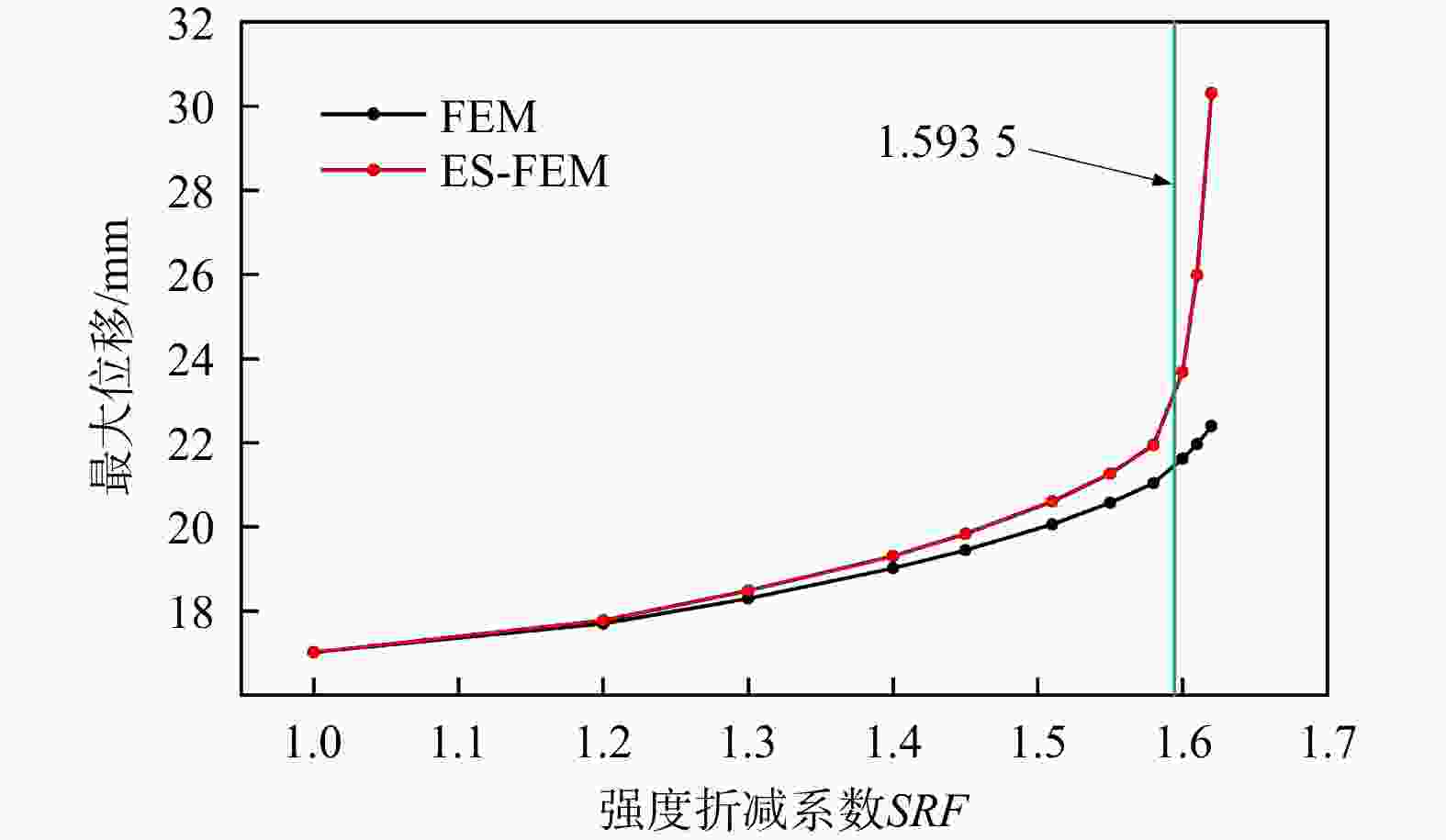
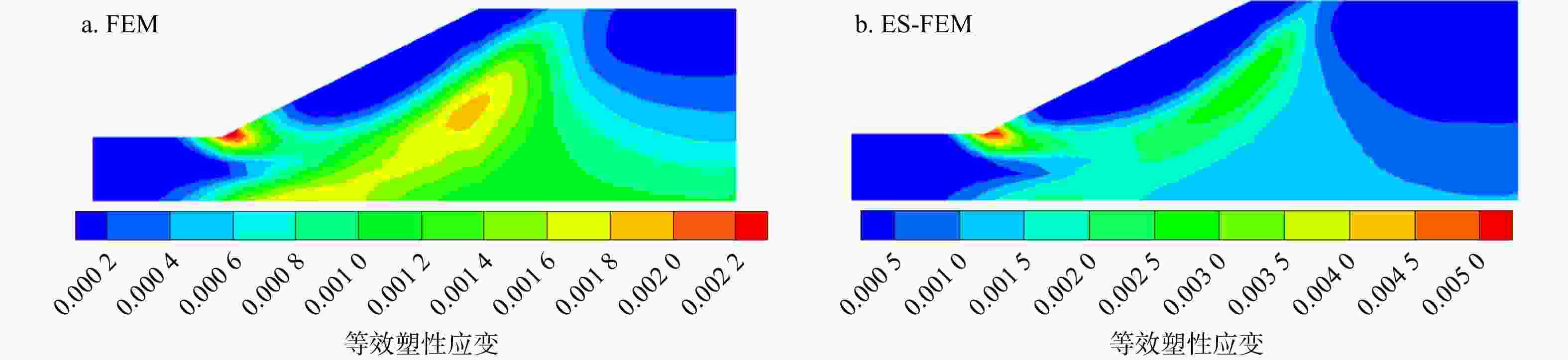
Results The classical bearing capacity model for the strip foundation and slope model was tested, and the numerical results align well with the reference solutions. The findings indicate that the calculation accuracy of the smooth finite element method is clearly superior to that of the traditional finite element method, confirming the feasibility and practicality of the proposed algorithm.
Conclusion In this work, the calculation model developed using the smooth finite element method significantly improves the calculation accuracy for rock and soil elastoplastic problems, while reducing the calculation error and stress misalignment caused by mesh distortion in traditional finite element methods.
-
图 1 边光滑有限元法光滑域划分示意图
Figure 1. Schematic diagram of smooth domain division for the ES-FEM
图 2 修正Mohr-Coulomb屈服准则在子午面内的拟合形式
$ \bar \sigma $为等效应力；$\sigma_{{\mathrm{m}}} $为平均应力；m为参数
Figure 2. Fitting form of the modified Mohr-Coulomb yield criterion in the meridional plane
图 3 修正M-C准则在$ \pi $平面上的屈服曲线
$ \theta $为洛德角；$ \sigma_1 $，$\sigma_2 $，$\sigma_3 $均为主应力；m为参数
Figure 3. Yield curve of the modified M-C criterion in the $ \pi $-plane
图 5 不同数值方法下压力系数与沉降中心的关系
Figure 5. Relationship between the pressure coefficient and center settlement under different numerical methods
图 6 不同数值方法下的塑性应变云图
Figure 6. Plastic strain contour maps under different numerical methods
图 7 不同数值方法下承载力误差与自由度的关系
Figure 7. Relationship between bearing capacity errors and degrees of freedom under different numerical methods
图 9 边坡最大位移与强度折减系数的关系
Figure 9. Relationship between the maximum displacement of the slope and the strength reduction coefficient
图 10 强度折减系数$ S R F = 1.6 $时的等效塑性应变分布
Figure 10. Distribution of the equivalent plastic strain with $S R F = 1.6$
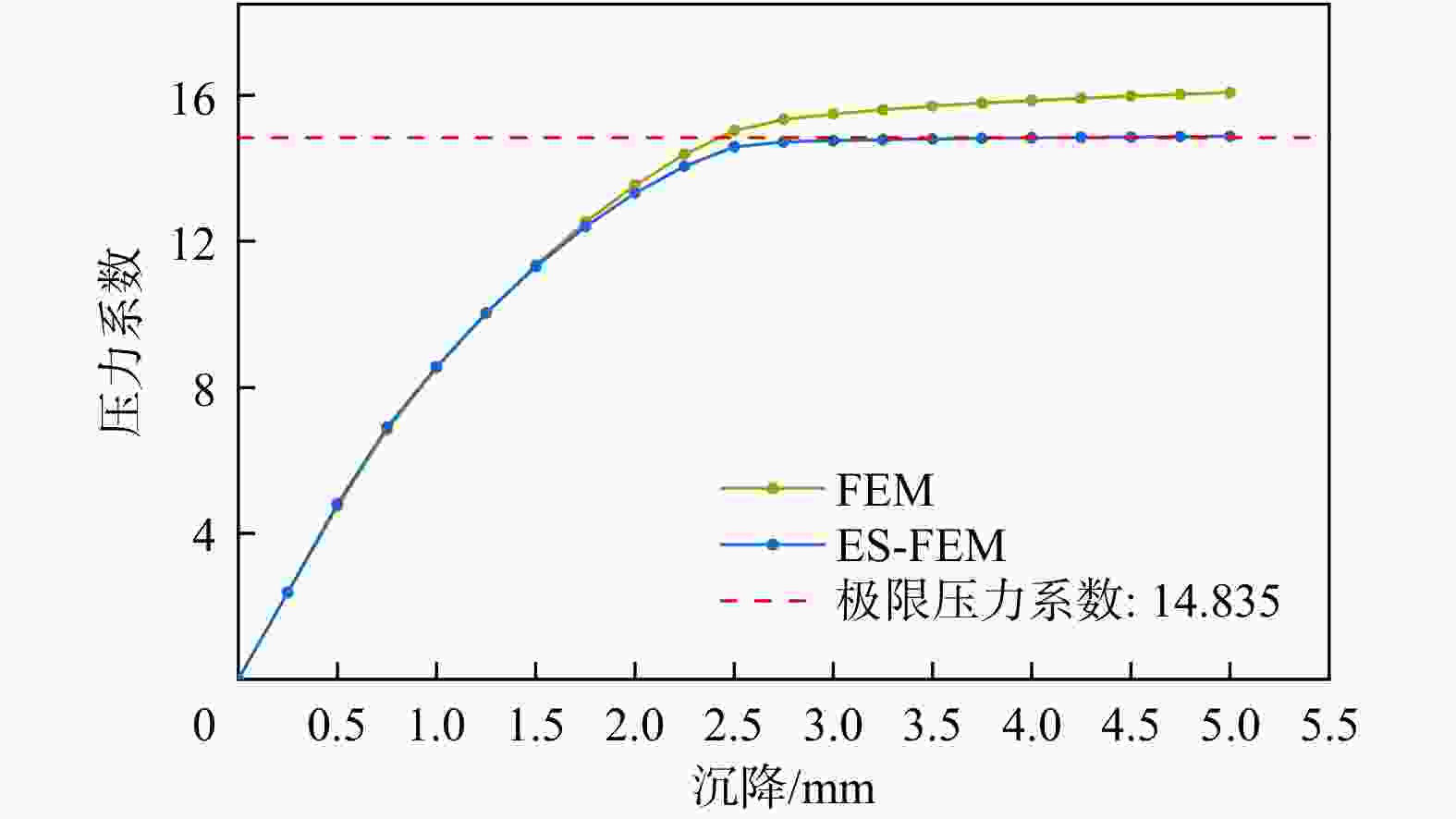
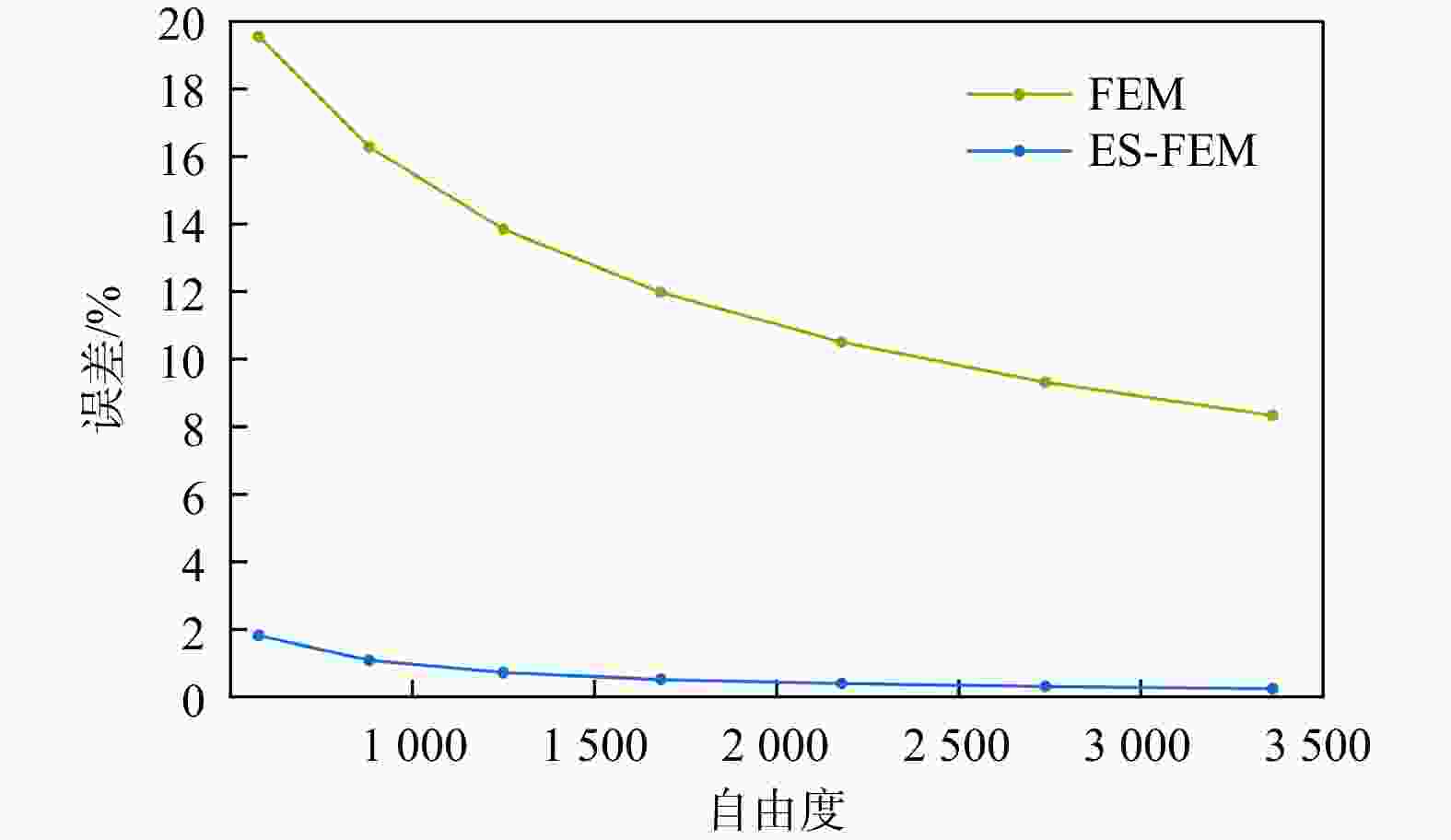
表 1 ES-FEM和FEM在不同自由度下的压力系数及误差
Table 1. Pressure coefficients and errors of ES-FEM and FEM under different degrees of freedom
自由度
DOFFEM ES-FEM 压力系数${L_F}$ 误差/% 压力系数${L_F}$ 误差/% 578 17.74 19.55 15.10 1.81 882 17.25 16.28 15.00 1.08 1250 16.89 13.84 14.94 0.72 1682 16.61 11.97 14.91 0.51 2178 16.39 10.50 14.89 0.40 2738 16.22 9.31 14.88 0.31 3362 16.07 8.33 14.87 0.24 
下载: 导出CSV
-
[1] LIU G R,NGUYEN T T,DAI K Y,et al. Theoretical aspects of the smoothed finite element method (SFEM)[J]. International Journal for Numerical Methods in Engineering,2007,71(8):902-930. doi: 10.1002/nme.1968 [2] CHEN J S,WU C T,YOON S,et al. A stabilized conforming nodal integration for Galerkin mesh-free methods[J]. International Journal for Numerical Methods in Engineering,2001,50(2):435-466. doi: 10.1002/1097-0207(20010120)50:2<435::AID-NME32>3.0.CO;2-A [3] LIU G R,DAI K Y,NGUYEN T T. A smoothed finite element method for mechanics problems[J]. Computational Mechanics,2007,39(6):859-877. doi: 10.1007/s00466-006-0075-4 [4] LIU G R,NGUYEN-THOI T,NGUYEN-XUAN H,et al. A node-based smoothed finite element method (NS-FEM) for upper bound solutions to solid mechanics problems[J]. Computers & Structures,2009,87(1/2):14-26. [5] LIU G R,NGUYEN-THOI T,LAM K Y. An edge-based smoothed finite element method (ES-FEM) for static,free and forced vibration analyses of solids[J]. Journal of Sound and Vibration,2009,320(4/5):1100-1130. [6] NGUYEN-THOI T,LIU G R,LAM K Y,et al. A face-based smoothed finite element method (FS-FEM) for 3D linear and geometrically non-linear solid mechanics problems using 4-node tetrahedral elements[J]. International Journal for Numerical Methods in Engineering,2009,78(3):324-353. doi: 10.1002/nme.2491 [7] CUI X Y,LIU G R,LI G Y,et al. Analysis of elastic–plastic problems using edge-based smoothed finite element method[J]. International Journal of Pressure Vessels and Piping,2009,86(10):711-718. doi: 10.1016/j.ijpvp.2008.12.004 [8] CUI X Y,LIU G R,LI G Y,et al. A smoothed finite element method (SFEM) for linear and geometrically nonlinear analysis of plates and shells[J]. Cmes-Computer Modeling in Engineering & Sciences,2008,28:109-126. [9] LIU J,ZHANG Z Q,ZHANG G. A smoothed finite element method (S-FEM) for large-deformation elastoplastic analysis[J]. International Journal of Computational Methods,2015,12(4):1540011. doi: 10.1142/S0219876215400113 [10] 霍泽楠. 基于Julia语言的弹塑性光滑有限元程序研制[D]. 北京:中国地质大学(北京),2021.HUO Z N. Development of elastoplastic smooth finite element program based on Julia language[D]. Beijing:China University of Geosciences(Beijing),2021. (in Chinese with English abstract [11] LIU G R,CHEN L,NGUYEN-THOI T,et al. A novel singular node-based smoothed finite element method (NS-FEM) for upper bound solutions of fracture problems[J]. International Journal for Numerical Methods in Engineering,2010,83(11):1466-1497. doi: 10.1002/nme.2868 [12] 王建明,李钊全,李博志. 基于光滑−扩展有限元法的裂纹扩展研究[J]. 郑州大学学报(工学版),2022,43(2):51-57.WANG J M,LI Z Q,LI B Z. Research on crack propagation based on smooth-extended finite element method[J]. Journal of Zhengzhou University (Engineering Science),2022,43(2):51-57. (in Chinese with English abstract [13] NGUYEN-XUAN H,LIU G R,NGUYEN-THOI T,et al. An edge-based smoothed finite element method for analysis of two-dimensional piezoelectric structures[J]. Smart Materials and Structures,2009,18(6):065015. doi: 10.1088/0964-1726/18/6/065015 [14] 朱婷婷,刘宝会,王刚,等. 基于边光滑有限元法的骨重建力电效应[J]. 医用生物力学,2022,37(4):631-637.ZHU T T,LIU B H,WANG G,et al. Electromechanical effects of bone remodeling based on edge smoothed finite element method[J]. Journal of Medical Biomechanics,2022,37(4):631-637. (in Chinese with English abstract [15] 黄湛勇,王刚,安玉民. 基于光滑有限元法的屏蔽微带线静电场研究[J]. 电子器件,2023,46(2):379-385. doi: 10.3969/j.issn.1005-9490.2023.02.014HUANG Z Y,WANG G,AN Y M. Study of the electrostatic field of shielded microstrip lines based on the smoothed finite element method[J]. Chinese Journal of Electron Devices,2023,46(2):379-385. (in Chinese with English abstract doi: 10.3969/j.issn.1005-9490.2023.02.014 [16] XUE B Y,WU S C,ZHANG W H,et al. A smoothed fem (s-fem) for heat transfer problems[J]. International Journal of Computational Methods,2013,10(1):1340001. doi: 10.1142/S021987621340001X [17] 马玉娥,陈鹏程,郭雯,等. 基于光滑有限元法的热−弹相场断裂研究[J]. 固体力学学报,2023,44(3):346-354.MA Y E ,CHEN P C,GUO W,et al. Study on thermo-elastic phase fracture modeling based on the cell-based smoothed finite element method[J]. Chinese Journal of Solid Mechanics,2023,44(3):346-354. (in Chinese with English abstract [18] 郑建校,段志善,周立明. 基于渐进均匀化的力−电−热耦合光滑有限元法研究[J]. 中南大学学报(自然科学版),2023,54(4):1325-1335. doi: 10.11817/j.issn.1672-7207.2023.04.011ZHENG J X,DUAN Z S,ZHOU L M. Research on thermo-electro-mechanical coupling smoothed finite element method based on asymptotic homogenization[J]. Journal of Central South University (Science and Technology),2023,54(4):1325-1335. (in Chinese with English abstract doi: 10.11817/j.issn.1672-7207.2023.04.011 [19] 李春光,赵晨,赵嵘. 端承桩法向接触互补问题的非光滑牛顿算法[J]. 华中科技大学学报(自然科学版),2023,51(7):13-17.LI C G,ZHAO C,ZHAO R. Nonsmooth Newton's algorithm for complementary problem normal contact of end-bearing pile[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition),2023,51(7):13-17. (in Chinese with English abstract [20] 范亚杰,李燕,李中潘,等. 接触与大变形问题的光滑有限元分析[J]. 应用数学和力学,2024,45(2):127-143.FAN Y J,LI Y,LI Z P,et al. Smoothed finite element analysis of contact and large deformation problems[J]. Applied Mathematics and Mechanics,2024,45(2):127-143. (in Chinese with English abstract [21] HE Z C,LIU G R,ZHONG Z H,et al. An edge-based smoothed finite element method (ES-FEM) for analyzing three-dimensional acoustic problems[J]. Computer Methods in Applied Mechanics and Engineering,2009,199(1/2/3/4):20-33. [22] 姚凌云,于德介,臧献国. 二维声学数值计算的光滑有限元法[J]. 机械工程学报,2010,46(18):115-120. doi: 10.3901/JME.2010.18.115YAO L Y,YU D J,ZANG X G. Smoothed finite element method for two-dimensional acoustic numerical computation[J]. Journal of Mechanical Engineering,2010,46(18):115-120. (in Chinese with English abstract doi: 10.3901/JME.2010.18.115 [23] 程嘉辉. 基于PWE/S-FEM的半无限声学超材料带隙仿真研究[D]. 天津:河北工业大学,2021.CHENG J H. Simulation of semi-infinite acoustic metamaterial band gap based on PWE/S-FEM[D]. Tianjin:Hebei University of Technology,2021. (in Chinese with English abstract [24] 柴应彬. 基于光滑有限元法的二维和三维维声学问题数值模拟研究[D]. 武汉:华中科技大学,2014.CHAI Y B. Research on numerical simulation of two-dimensional and three-dimensional acoustic problems based on smooth finite element method[D]. Wuhan:Huazhong University of Science and Technology,2014. (in Chinese with English abstract [25] OWEN D R J,HINTON E. Finite elements in plasticity:Theory and practice[M]. Swansea:Pineridge Press,1980. [26] 贾善坡,陈卫忠,杨建平,等. 基于修正Mohr-Coulomb准则的弹塑性本构模型及其数值实施[J]. 岩土力学,2010,31(7):2051-2058.JIA S P,CHEN W Z,YANG J P,et al. An elastoplastic constitutive model based on modified Mohr-Coulomb criterion and its numerical implementation[J]. Rock and Soil Mechanics,2010,31(7):2051-2058. (in Chinese with English abstract [27] ABBO A J,SLOAN S W. A smooth hyperbolic approximation to the Mohr-Coulomb yield criterion[J]. Computers & Structures,1995,54(3):427-441. [28] ZHU D Y,LEE C F,LAW K T. Determination of bearing capacity of shallow foundations without using superposition approximation[J]. Canadian Geotechnical Journal,2003,40(2):450-459. doi: 10.1139/t02-105 [29] MICHALOWSKI R L,YOU L Z. Non-symmetrical limit loads on strip footings[J]. Soils and Foundations,1998,38(4):195-203. doi: 10.3208/sandf.38.4_195 [30] BOLTON M D,LAU C K. Vertical bearing capacity factors for circular and strip footings on Mohr-Coulomb soil[J]. Canadian Geotechnical Journal,1993,30(6):1024-1033. doi: 10.1139/t93-099 [31] KUMAR J. Nγ for rough strip footing using the method of characteristics[J]. Canadian Geotechnical Journal,2003,40(3):669-674. doi: 10.1139/t03-009 [32] KUMAR J,KOUZER K M. Effect of footing roughness on bearing capacity factor Nγ[J]. Journal of Geotechnical and Geoenvironmental Engineering,2007,133(5):502-511. doi: 10.1061/(ASCE)1090-0241(2007)133:5(502) [33] VAN BAARS S. The inclination and shape factors for the bearing capacity of footings[J]. Soils and Foundations,2014,54(5):985-992. doi: 10.1016/j.sandf.2014.09.004 [34] 郑宏,田斌,刘德富,等. 关于有限元边坡稳定性分析中安全系数的定义问题[J]. 岩石力学与工程学报,2005,24(13):2225-2230. doi: 10.3321/j.issn:1000-6915.2005.13.004ZHENG H,TIAN B,LIU D F,et al. On definitions of safety factor of slope stability analysis with finite element method[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(13):2225-2230. (in Chinese with English abstract doi: 10.3321/j.issn:1000-6915.2005.13.004 [35] 陈飞宇,董利飞,王苗,等. 基于灰色马尔科夫模型的地基承载力预测[J]. 地质科技通报,2022,41(3):222-227.CHEN F Y,DONG L F,WANG M,et al. Prediction of foundation bearing capacity based on grey Markov model[J]. Bulletin of Geological Science and Technology,2022,41(3):222-227. (in Chinese with English abstract [36] 周少伟,边小卫,李卫波,等. 考虑降雨条件陕北Q2黄土斜坡稳定性的非线性劣化研究[J]. 地质科技通报,2024,43(3):218-226.ZHOU S W,BIAN X W,LI W B,et al. Nonlinear degradation of stability of Q2 considering rainfall conditions loess slopes in northern Shaanxi[J]. Bulletin of Geological Science and Technology,2024,43(3):218-226. (in Chinese with English abstract [37] SU Z N,SHAO L T. A three-dimensional slope stability analysis method based on finite element method stress analysis[J]. Engineering Geology,2021,280:105910. doi: 10.1016/j.enggeo.2020.105910 [38] FU X D,SHENG Q,ZHANG Y H,et al. Computation of the safety factor for slope stability using discontinuous deformation analysis and the vector sum method[J]. Computers and Geotechnics,2017,92:68-76. doi: 10.1016/j.compgeo.2017.07.026 [39] 李钰,陈明亮,黄会宝,等. 新华滑坡变形演化规律与预警判据[J]. 地质科技通报,2024,43(3):227-239.LI Y,CHEN M L,HUANG H B,et al. Deformation evolution law and early warning criterion of Xinhua landslide[J]. Bulletin of Geological Science and Technology,2024,43(3):227-239. (in Chinese with English abstract [40] 易富,孟兴涛,赵文华,等. 基于因素空间的露天采坑边坡稳定性评价[J]. 地质科技通报,2023,42(5):1-9.YI F,MENG X T,ZHAO W H,et al. Evaluation of slope stability of open pit based on factor space[J]. Bulletin of Geological Science and Technology,2023,42(5):1-9. (in Chinese with English abstract [41] PRANDTL L. Hauptaufsätze:Über die Eindringungsfestigkeit (Härte) plastischer Baustoffe und die Festigkeit von Schneiden[J]. ZAMM - Journal of Applied Mathematics and Mechanics,1921,1(1):15-20. doi: 10.1002/zamm.19210010102 -
下载:
点击查看大图
计量
- 文章访问数: 22
- PDF下载量: 0
- 被引次数: 0
