随着我国进入“十四五”时期，在基础建设、交通、水利等方面涌现了大批的重大工程建设项目，这些重大项目大多集中在西部地质条件复杂的区域，随之而来的工程问题大多呈现复杂化、极端化的特点，给工程推进带来了极大的困难。工程问题大多与岩土体的复杂性息息相关，解决工程问题的核心是正确地认识和评价岩土材料的发展规律，并以恰当的手段对其发展形式做出预测和评价。

近年来，随着计算机技术和计算力学的发展，数值分析也逐步成为了解决岩土工程问题的一种重要手段。在数值分析中，常采用有限元法来实现模型的弹塑性计算，而在有限元法中，低阶单元，特别是二维问题中的三角形单元和三维问题中的四面体单元，由于其具有易于剖分、计算效率高及网格剖分效果良好等特点，对解决岩土工程问题具有极大的吸引力。然而，在使用有限元法求解非线性问题时，由于存在收敛问题、网格畸变和体积锁定等缺陷，这一类低阶线性单元的使用有很大的局限性，因此一部分专家将目光转向了开发优化这些线性单元之上。

LIU等^[1]提出的光滑有限元法是一种有效改进线性单元求解精度和收敛速度的算法，其本质是将传统有限元法与无网格法中的应变光滑技术^[2]结合，在光滑域上采用应变光滑技术计算系统刚度矩阵，能够有效改进有限元结构刚度。LIU等基于该理论提出了一系列的光滑有限元数值算法，包括光滑子单元域有限元法（CS-FEM）^[3]、结点光滑有限元法（NS-FEM）^[4]、边光滑有限元法（ES-FEM）^[5]和面光滑有限元法（FS-FEM）^[6]等。光滑有限元法目前已经在黏弹塑性^[7]、弹塑性^[8-10]、断裂力学^[11-12]、压电结构^[13-15]、传热^[16-18]、接触^[19-20]和声学^[21-24]等多个领域中得到了广泛的应用。在众多光滑有限元算法中，NS-FEM和ES-FEM被广泛使用，其中ES-FEM具有空间离散稳定性和时间响应稳定性，相比于FEM模型中偏硬的刚度以及NS-FEM中过软的刚度，ES-FEM模型的刚度更接近结构的实际刚度，可以对动态问题给出精确、稳定的结果，对静态问题给出超精确的结果。

岩土材料一般遵循Drucker-Prager屈服准则、Mohr-Coulomb屈服准则（简称M-C屈服准则）或Zienkiewicz-Pande屈服准则等。其中，M-C屈服准则是目前在岩土领域运用最广泛的屈服准则，它能较好地描述岩土材料的强度特性和破坏行为，并且考虑了材料抗压强度与抗拉强度的差异以及静水压力影响^[25-26]。但是，传统M-C屈服准则在主应力空间的屈服面边缘和顶端存在奇异点，在数值计算中容易产生奇异性问题，使得对应的弹塑性应力积分效率低下甚至失败。故本研究拟采用ABBO等^[27]提出的一种修正M-C屈服准则，该方法通过构建一种双曲屈服面来拟合M-C屈服面，消除了M-C屈服面中的奇异点，使得屈服面在所有的应力状态下都是连续和可微的，能够极大地提升弹塑性应力积分的稳定性。由于修正M-C准则在处理奇异点时，屈服面的数值实现存在一定的收敛问题，故本研究采用线性搜索优化算法来增强算法的迭代收敛效率。

综上所述，本研究将一种修正M-C屈服准则与ES-FEM结合，建立了求解岩土体弹塑性问题的计算程序。地基承载力和边坡稳定性问题是岩土工程中常见的问题^[28-40]，故本研究采用经典的条形基础承载力模型和边坡模型作为数值算例进行分析。结果表明本研究程序的计算结果与对应岩土问题的解析解均吻合较好，验证了本研究程序的可行性与实用性，且证明了ES-FEM的计算精度明显优于FEM。

1.   光滑有限元法理论及公式

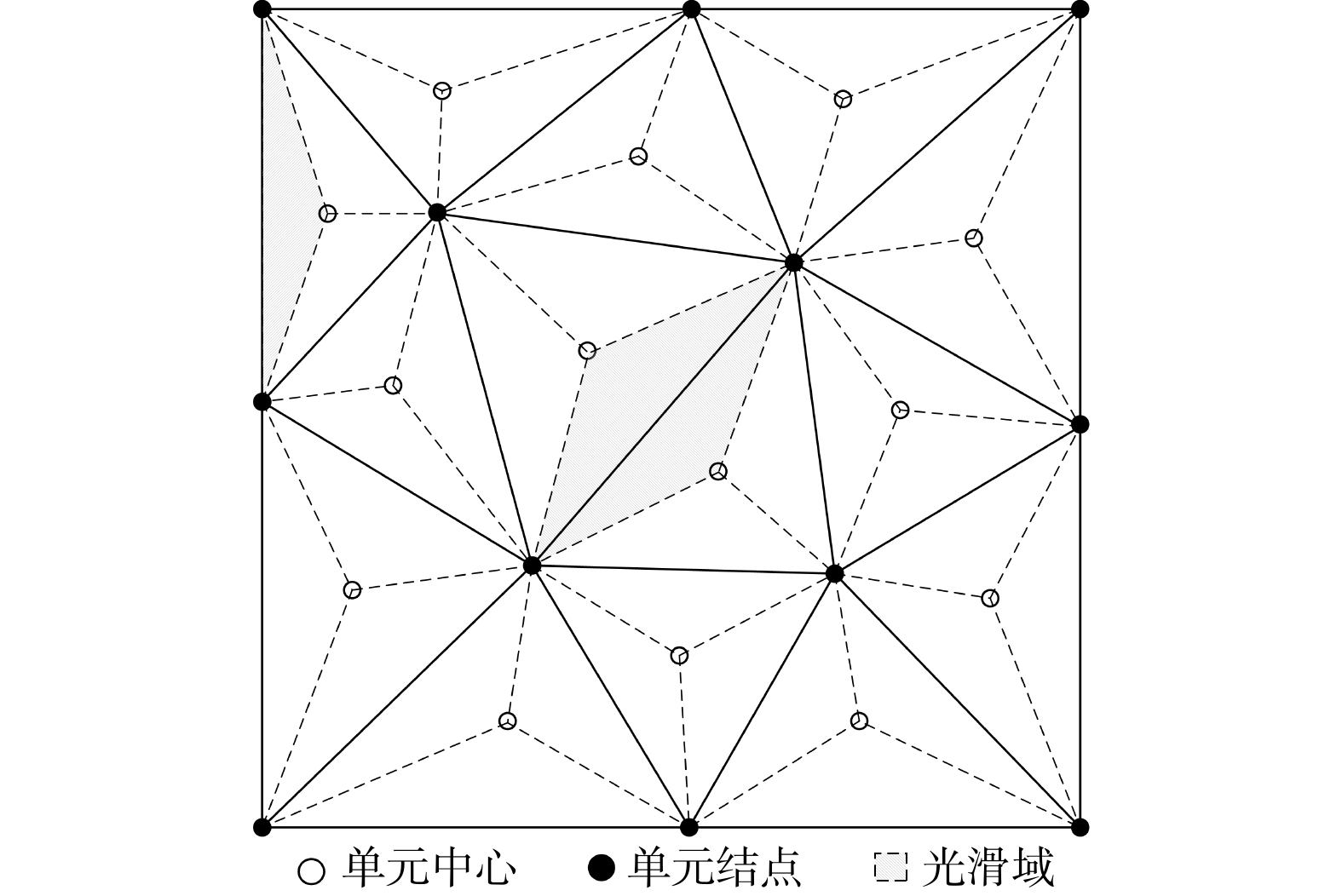
光滑域的划分是实现光滑有限元法的关键，本节以二维的边光滑有限元法为例对其划分形式进行介绍：以单元边为基准划分光滑域，光滑域为基准边上的2个结点和相邻单元面的形心点连接而成的区域，图中实线为单元边，虚线为单元形心与单元结点的连线，如图1所示。假设单元边总数为${N_{\rm eg}}$，光滑域总数为${N_ {\rm s}}$，单元边与光滑域一一对应，即：${N_ {\rm s}} = {N_{\rm{eg}}}$。

图  1  边光滑有限元法光滑域划分示意图

Figure  1.  Schematic diagram of smooth domain division for the ES-FEM

下载: 全尺寸图片 幻灯片

与传统有限元法相同，光滑有限元法也是通过构造形函数来建立问题域的位移场：

式中：$\boldsymbol{\bar u(x)}$为位移函数；$\boldsymbol x$为问题域内的任意坐标向量；${N_n}$为问题域中的结点数目；${\boldsymbol{N}_I}(\boldsymbol{x})$为结点$I$的形函数；${\boldsymbol{\bar d}_I}$为结点$I$的位移向量；$\boldsymbol{N(x)}$为问题域的形函数矩阵；$\boldsymbol{\bar d}$为问题域的位移向量矩阵。

对于光滑有限元法中常用的三角形单元和四面体单元，可以直接使用传统有限元法中的三角形单元和四面体单元的线性形函数。

利用应变光滑技术创建光滑应变场，当相容应变场易得到时，光滑应变场$(\bar \varepsilon )$可通过修正相容应变场获得：

式中：$\boldsymbol{\tilde \varepsilon (x)}$为传统有限元法中的相容应变场；$\varOmega_k^s$为一个包含$\boldsymbol{x_k}$的光滑域；$\boldsymbol{x_k}$为光滑域的基准坐标向量；$\overline W(\boldsymbol{x_k} - \boldsymbol{x})$为与$\boldsymbol{x_k}$有关的光滑函数，可定义为：

式中：$A_k^s = \int {_{\Omega _k^s}{\mathrm{d}}\varOmega}$，为该光滑域的面积。

在相容应变场难以求取时，光滑应变场也可通过对位移场求导得到：

式中：$\boldsymbol{L_d}$为微分算子矩阵。

当相容应变场易获得时，假设光滑域$\varOmega_k^s$中的光滑应变场是一个常数，则由式（2）和式（3）得：

由式（5）可知，当获得了光滑域中的相容应变场之后，可通过对其进行体积平均来获得$\boldsymbol{x_k}$处的光滑应变场，即光滑域$\varOmega _k^s$中的光滑应变场。通常情况下仅有位移场，假定位移场在$\varGamma _k^s$上是连续的，利用高斯散度定理将式（4）从域积分转化为线积分得：

式中：$\varGamma _{{k}}^s$为光滑域$\varOmega _k^s$的边界；$\boldsymbol{L_n}(\boldsymbol{x})$为外法向分量矩阵：

式中：${n_x}$，${n_y}$分别为$\boldsymbol{L_n}(\boldsymbol{x})$的$x$轴和$y$轴的外法向分量。

将式（1）代入式（6），可得：

式中：${\bar {\boldsymbol B} (\boldsymbol{x})}$为全局光滑应变矩阵；${\bar {\boldsymbol B}_{\boldsymbol I}}(\boldsymbol{x})$是结点$I$处的光滑应变矩阵。在模型中，只有$\boldsymbol x$支持光滑域$\Omega _k^s$时，${\bar {\boldsymbol B}_{\boldsymbol I}}(\boldsymbol{x})$是非零的。${\bar {\boldsymbol B}_ {\boldsymbol I}}(\boldsymbol{x})$可通过在光滑边界上进行形函数线积分得到：

式中：

此外，当位移函数连续，且相容应变矩阵${\tilde{\boldsymbol{B_I}}}(\boldsymbol{x})$容易获得时，可按照式（6）中光滑应变场$\boldsymbol{\bar \varepsilon}$的定义，得到光滑应变矩阵${\bar{\boldsymbol{B}}_{\boldsymbol{I}}}$与上述相容应变矩阵${\tilde{\boldsymbol{B}}_{\boldsymbol{I}}}(\boldsymbol{x})$的关系：

光滑有限元法的总体平衡方程可通过使用光滑伽辽金弱化形式得到：

式中：$\boldsymbol{b}$为问题域上的外部体力；${\boldsymbol{D}_ {\rm e}}$为弹性矩阵；$\boldsymbol{\bar u}$为问题域中的位移场；$\boldsymbol{t}$为边界上的外部牵引力。

将式（1）和式（8）代入式（12）并化简可得标准的离散方程组：

式中：$\boldsymbol{\bar d}$为模型中所有的结点位移向量；$\boldsymbol{\tilde f}$为模型所受的载荷向量；$\boldsymbol{\bar K}$为光滑刚度矩阵：

2.   修正Mohr-Coulomb屈服准则

Mohr-Coulomb屈服准则是Coulomb剪切强度准则的推广，其形式由下式定义：

式中：${\tau _n}$为极限抗剪强度；${\sigma _n}$为剪切面上的正应力，以拉为正；$C$为黏聚力；$\varphi$为内摩擦角。

假定物体中某一点的3个主应力分别为${\sigma _1}$，${\sigma _2}$，${\sigma _3}$，且满足${\sigma _1} \gt {\sigma _2} \gt {\sigma _3}$，则M-C屈服准则可表示为：

为便于进行数值计算，Nayak和Zienkiewicz将屈服准则改为由应力不变量表示的形式：

式中：${\sigma _{\mathrm{m}}}$为平均应力，${\sigma _{\mathrm{m}}} = {I_1}/3$，${I_1}$为应力张量的第一不变量；$\bar \sigma$为等效应力，$\bar \sigma = \sqrt {{J_2}}$，${J_2}$为应力偏量的第二不变量；$\theta$为洛德角；$K(\theta )$定义为：

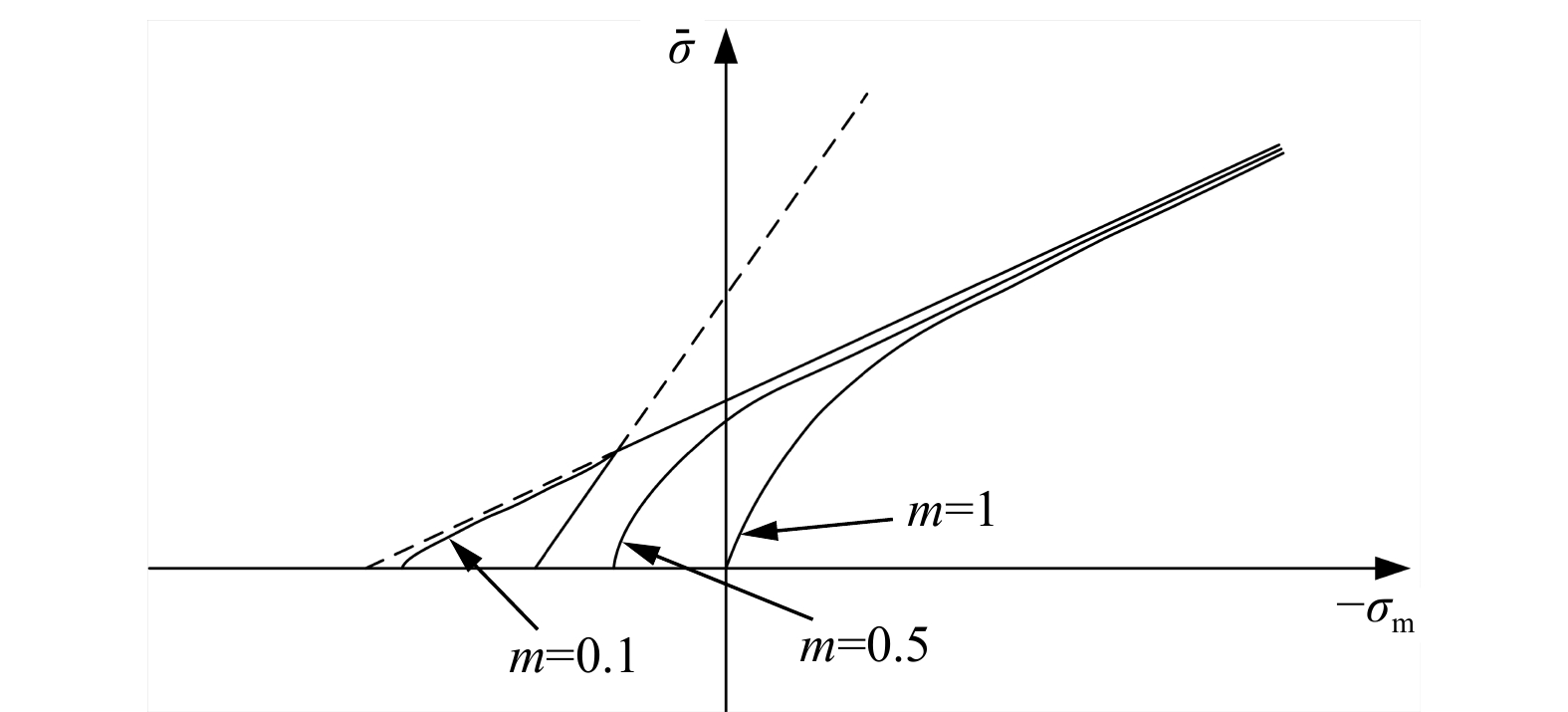
传统M-C屈服准则的屈服面边缘和顶端的角点处，存在导数不连续问题，将这样的点称为屈服面上的奇异点，而在数值计算中，奇异点是必须要消去的。如图2所示，对于屈服面顶端处的奇异点问题，ABBO等^[27]采用了双曲线进行拟合，并通过调节参数$m$使得函数尽可能接近传统M-C屈服准则，代数形式为：

图  2  修正Mohr-Coulomb屈服准则在子午面内的拟合形式

$\bar \sigma$为等效应力；$\sigma_{{\mathrm{m}}}$为平均应力；m为参数

Figure  2.  Fitting form of the modified Mohr-Coulomb yield criterion in the meridional plane

下载: 全尺寸图片 幻灯片

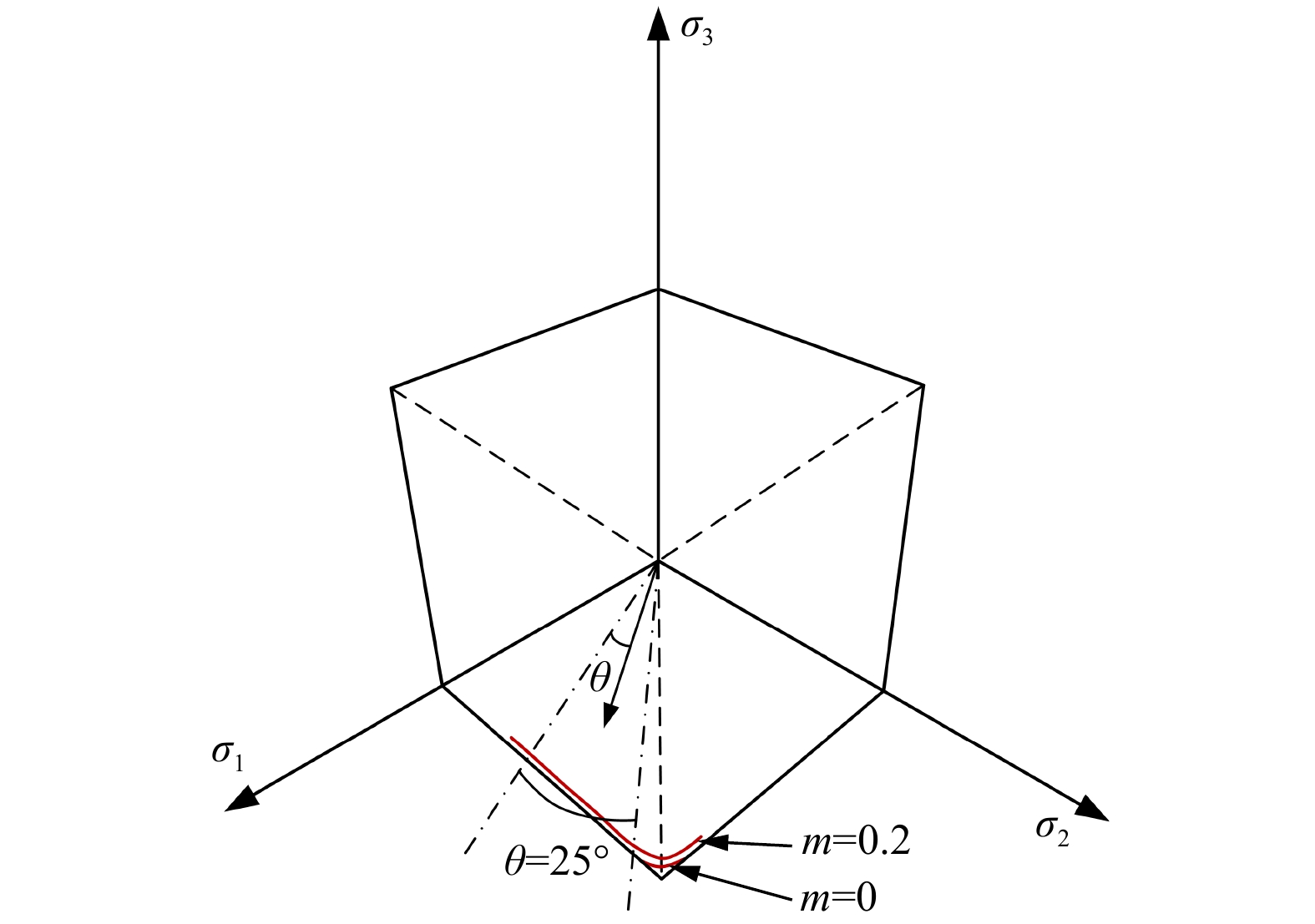
对于屈服面边缘处的奇异性问题，则通过将式（19）改写为一个分段函数，在边缘处采用一种简单的三角逼近对奇异点进行光滑处理，如图3所示，代数形式为：

图  3  修正M-C准则在$\pi$平面上的屈服曲线

$\theta$为洛德角；$\sigma_1$，$\sigma_2$，$\sigma_3$均为主应力；m为参数

Figure  3.  Yield curve of the modified M-C criterion in the $\pi$-plane

下载: 全尺寸图片 幻灯片

式中：${\theta _{\rm T}}$为分段函数的分界点；$A$和$B$的定义为：

式中：

式（19）和式（20）定义了一个完整双曲屈服函数，其在所有的应力状态下都是连续且可微的，并且可以通过调节参数$m$和${\theta _{\rm T}}$来调整与传统M-C屈服准则的趋近度。显然，当$m = 0$且${\theta _{\rm T}} = {30^ \circ }$时，就恢复为传统的M-C屈服准则。ABBO等^[27]对参数$m$进行了精度分析：$m \lt 0.25$时，修正M-C的结果与传统M-C的结果接近；$m = 0.05$时，结果基本一致，但$m$取值过小会在一定程度上影响计算收敛性。故本研究综合考虑求解效率和求解精度，选取$m = 0.1$。

在弹塑性数值分析中，还需要考虑的一个关键问题是塑性势函数的形式，本研究的修正M-C屈服准则在数值实现时采用与屈服函数一致的塑性势函数：

式中：$\varPhi$为剪胀角；$K'(\theta )$与$K(\theta )$形式一致，区别在于使用剪胀角$\varPhi$代换内摩擦角$\varphi$。

3.   弹塑性求解方式

最近点投影法是目前研究中常用的方法，其数学严格、计算结果与迭代路径无关，构建的一致弹塑性切线模量具有二阶收敛性。但其在强非线性情况下收敛性较差，故对最近点投影法中在强非线性状态下存在的收敛性问题，本研究采用Newton法结合线性搜索，保证其收敛。

3.1   最近点映射法

最近点投影法实质上是一种向后欧拉映射算法，利用迭代，得到满足塑性流动法则和屈服条件的解：

式中：$\Delta {\boldsymbol{\varepsilon} _{\rm p}}$为塑性应变增量；$\Delta \lambda$为塑性乘子；$\boldsymbol{b}$为塑性势函数对应力的一阶导数。

定义残差${r}$和自变量${\textit{z}}$为：

式中：$\Delta\boldsymbol{\sigma}$为应力增量；$\Delta\boldsymbol{\sigma}_{\rm p}$表示塑性应变增量$\Delta \varepsilon_{\mathrm{p}}$引起的应力改变量，定义为：

式中：$\Delta \boldsymbol{\varepsilon}$为应变增量。

根据式（25），可得$r$对${\textit{z}}$求偏导为：

式中：$\boldsymbol{I}$为单位矩阵；$\boldsymbol{H}$为塑性势函数对应力的二阶导数；$\boldsymbol{a}$为屈服函数对应力的一阶导数。

易知，当${r} = 0$时，${\textit{z}}$所指代的应力和塑性乘子将同时满足塑性流动法则和屈服条件。求解形式采用Newton迭代法，迭代格式如下：

3.2   一致弹塑性切线模量

在最近点投影法中采用基于本构积分算法的一致弹塑性切线模量，该模量可与路径无关的变量更新格式保持一致，且保留了Newton迭代的二次收敛速度，并在一定程度上改善应力偏离现象。

将式（24）和式（26）改写为增量形式：

增量一致性条件为：

将式（30）代入式（29），得到：

式中：

将式（32）代入增量一致性条件（式（31）），并求解${\mathrm{d}}(\Delta \lambda )$，得到：

将式（34）代入式（32），得到：

式中：

$\boldsymbol{D}_{{\mathrm{ep}}}$即为所求的一致弹塑性切线模量。

3.3   线性搜索

在前2节中给出了最近点投影法的迭代求解形式和一致弹塑性切线模量，如果弹性预测值在实际值附近，则上述求解方式可直接给出真实解。但是在强非线性条件下，单纯的Newton法迭代难以收敛，此时采用线性搜索能够保证程序的收敛。

在3.1节Newton迭代的基础上，引入一个步长系数$\alpha$，即将式（28）改写为：

式中：

式（37）中，步长系数$\alpha$的作用主要是保证迭代始终朝着误差减少的方向进行。

定义误差平方和函数$\phi (\alpha )$来判断步长是否合理，形式如下：

在求解过程中，残差的下降等价于误差平方和函数的下降，并且误差平方和函数是一个凸函数，必然可以求得其最优解。求解误差平方和函数的下降问题，需要其导数，形式如下：

由于平方和函数形式的复杂性，只依靠其导数形式往往难以求解，故在此使用最优化理论中的Wolfe条件进行求解：

式中：${c_1}$和${c_2}$均为常数，针对一般最优化问题，一般取值为$c_1 = 0.000\ 1$，${c_2} = 0.9$。

4.   数值算例

4.1   条形基础承载力

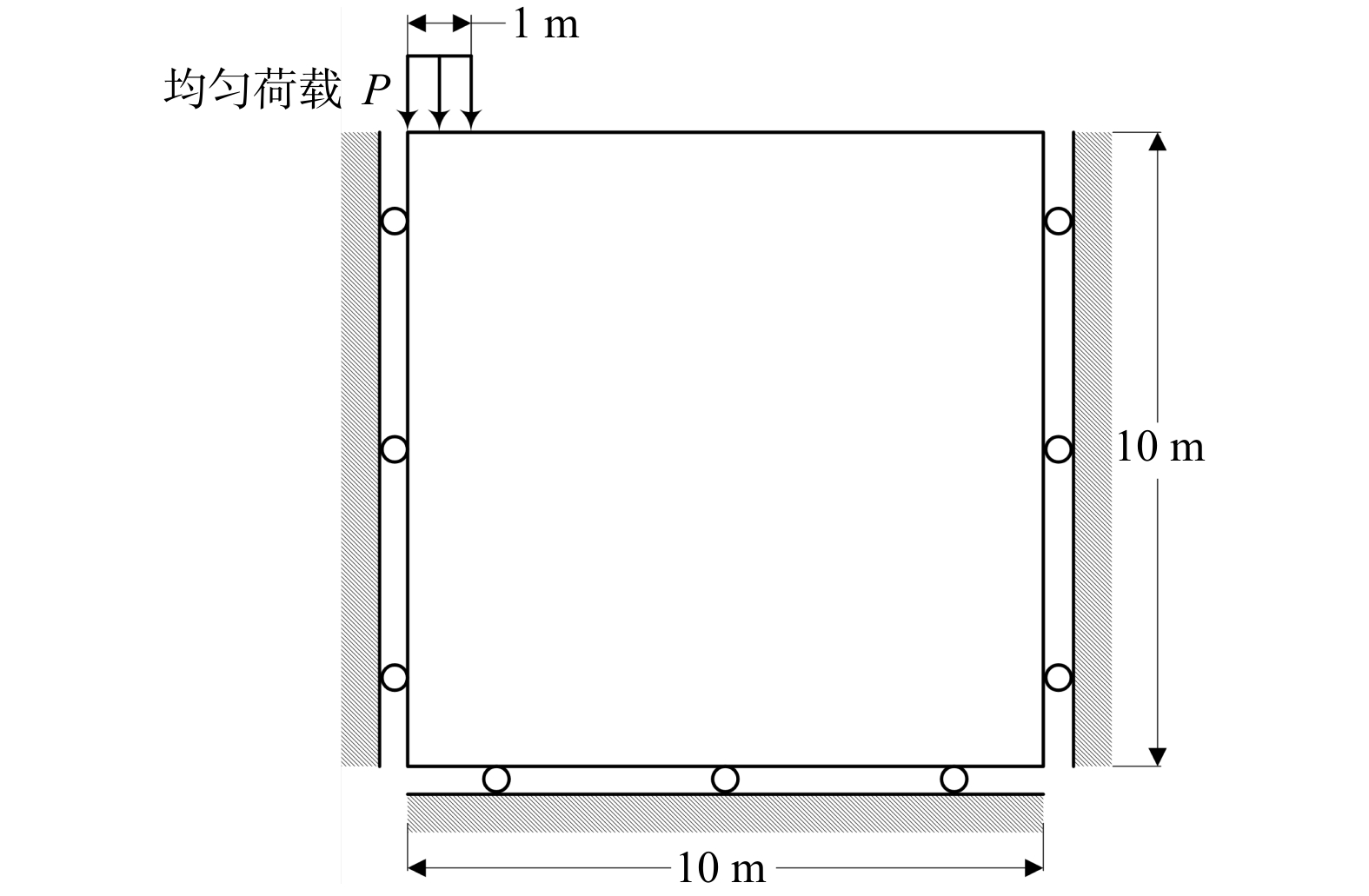
假定模型材料是失重、各向同性的，遵循Mohr-Coulomb理想弹塑性条件，并且不考虑基础与土界面之间的摩擦。利用基础的对称性，只考虑一半的基础，模型几何参数如图4所示，在模型左上部施加均匀荷载P，在模型下部和模型左右两侧施加法向约束。材料参数为：杨氏模量$E = 1 \times {10^7}\ {\mathrm{kPa}}$，泊松比$v = 0.48$，黏聚力$C = 490\ {\mathrm{kPa}}$，内摩擦角$\varphi = {20^ \circ }$。

图  4  条形基础计算模型

Figure  4.  Computational model of strip footing

下载: 全尺寸图片 幻灯片

条形基础的理论极限压力（P_lim）由PRANDTL^[41]解给出：

将本模型的参数代入式（42），得到的理论极限压力系数（L_F）为：

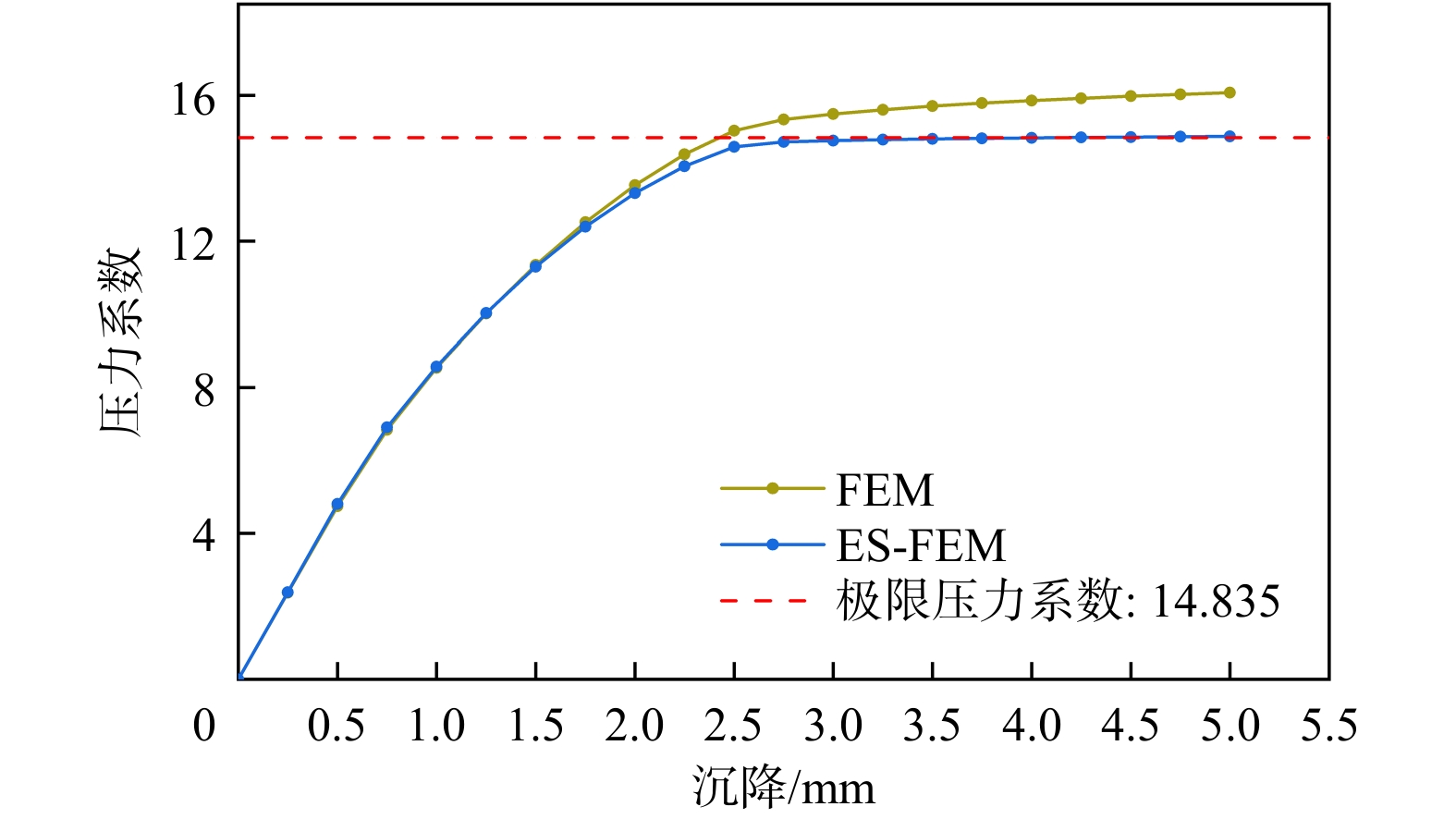
采用关联流动法则，分别使用FEM程序和ES-FEM程序进行分析，以验证ES-FEM的优势。同一网格状态下，不同数值方法计算的压力系数与沉降中心曲线如图5所示。在相同的网格状态下，能明显看出ES-FEM所求的极限载荷与理论值的吻合度远超过FEM，在计算过程中ES-FEM明显比FEM更快达到收敛。其中，FEM所求的极限载荷过大，体现了其刚度相较于模型真实刚度过硬，相比之下，ES-FEM的刚度更接近模型的真实刚度。塑性应变云图如图6所示，2种方法的最大塑性应变都集中在地基边缘位置，符合实际发展趋势，且从ES-FEM的塑性云图中可以明显看出塑性区有形成贯通的趋势。

图  5  不同数值方法下压力系数与沉降中心的关系

Figure  5.  Relationship between the pressure coefficient and center settlement under different numerical methods

下载: 全尺寸图片 幻灯片

图  6  不同数值方法下的塑性应变云图

Figure  6.  Plastic strain contour maps under different numerical methods

下载: 全尺寸图片 幻灯片

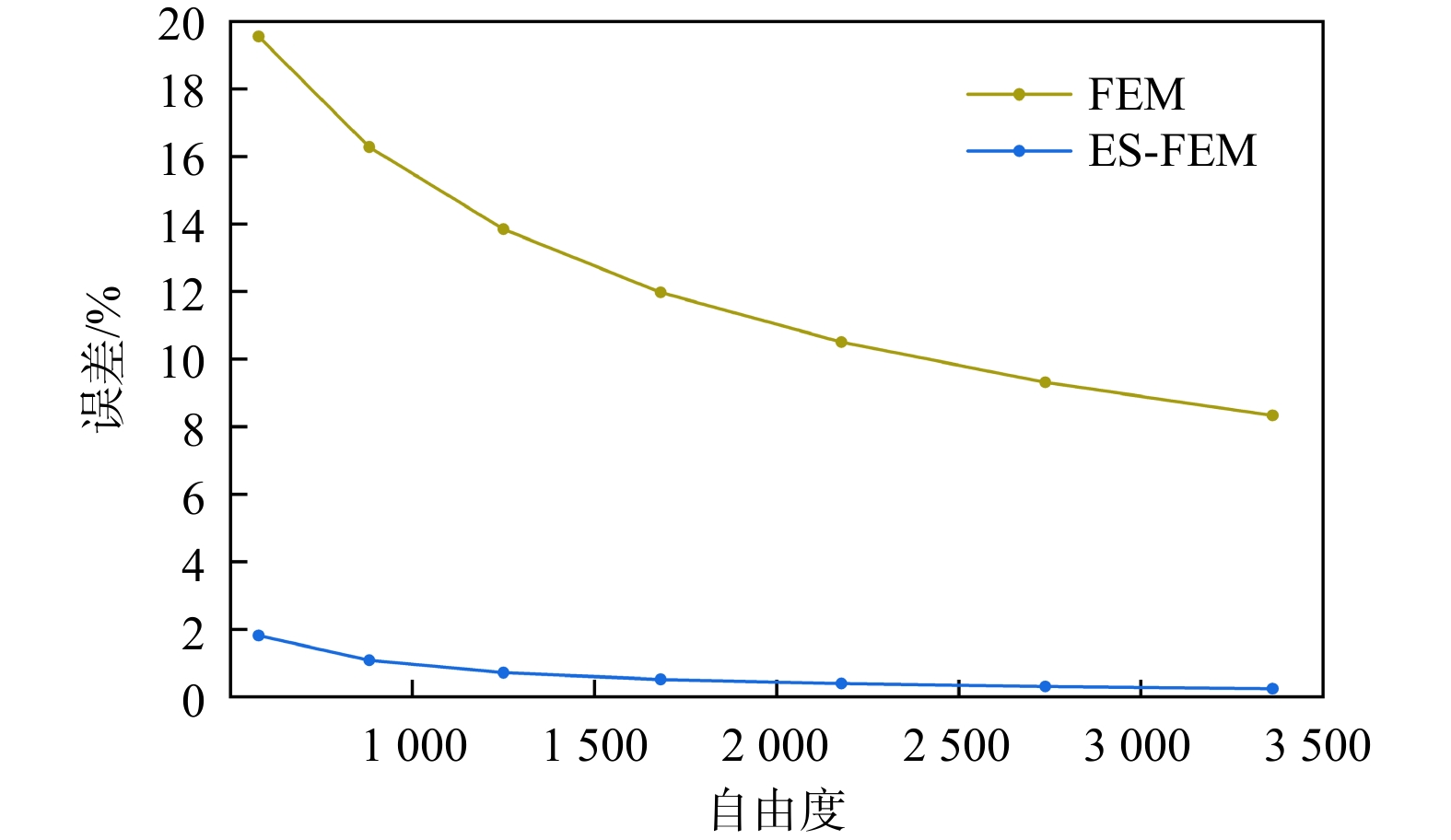
对该条形基础承载力模型以不同网格尺寸（以自由度来衡量）进行划分，采用不同方法计算的压力系数及与解析解的误差数据如表1所示，不同方法计算的承载力误差与自由度的关系如图7所示。ES-FEM在自由度578的状态下，求解误差为1.81%，而FEM由于刚度过硬，即使在自由度3362的状态下，求解误差仍有8.33%，此时ES-FEM的误差仅为0.24%。可知，ES-FEM在稀疏网格状态下便能取得较好的计算精度。

表  1  ES-FEM和FEM在不同自由度下的压力系数及误差

Table  1.  Pressure coefficients and errors of ES-FEM and FEM under different degrees of freedom

自由度 DOF	FEM			ES-FEM
	压力系数${L_F}$	误差/%		压力系数${L_F}$	误差/%
578	17.74	19.55		15.10	1.81
882	17.25	16.28		15.00	1.08
1250	16.89	13.84		14.94	0.72
1682	16.61	11.97		14.91	0.51
2178	16.39	10.50		14.89	0.40
2738	16.22	9.31		14.88	0.31
3362	16.07	8.33		14.87	0.24

下载: 导出CSV 

| 显示表格

图  7  不同数值方法下承载力误差与自由度的关系

Figure  7.  Relationship between bearing capacity errors and degrees of freedom under different numerical methods

下载: 全尺寸图片 幻灯片

4.2   边坡稳定性

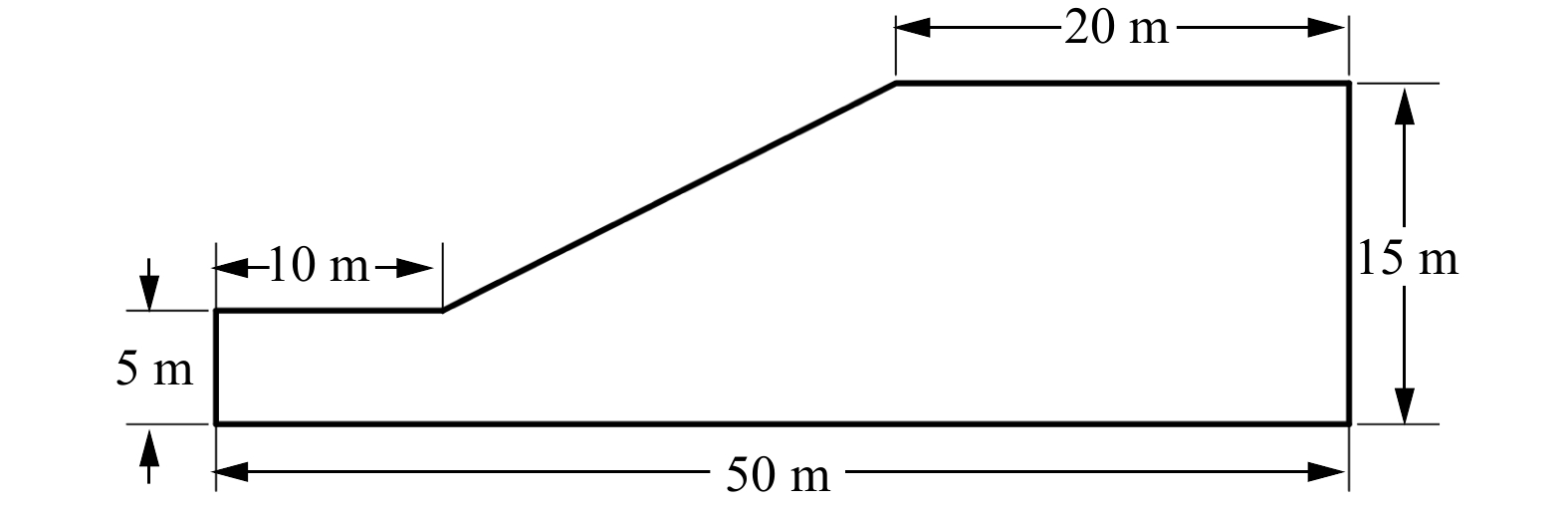
假定材料各向同性，遵循Mohr-Coulomb理想弹塑性条件，使用关联的流动法则。模型几何参数如图8所示。材料参数为：杨氏模量$E = 1 \times {10^5}\ {\mathrm{kPa}}$；泊松比$v = 0.30$；黏聚力$C = 15\ {\mathrm{kPa}}$；内摩擦角$\varphi = {20^ \circ }$；土体容重$\gamma = 20\ {\mathrm{kN}}/{{\mathrm{m}}^3}$。

图  8  边坡计算模型

Figure  8.  Computational model of slope

下载: 全尺寸图片 幻灯片

笔者基于商业软件Geo-Slope采用Bishop法求得安全系数为1.595，采用Morgenstern法求得安全系数为1.592作为参考解，并考虑采用强度折减法计算边坡的安全系数${F_{\mathrm{s}}}$，通过使用强度折减系数（SRF）不断减小强度参数来削弱土体，直到土体丧失稳定性，以最终的强度折减系数来近似表征边坡安全系数，求解形式为：

式中：$SRF$的最终收敛值即为边坡的安全系数${F_{\mathrm{s}}}$。

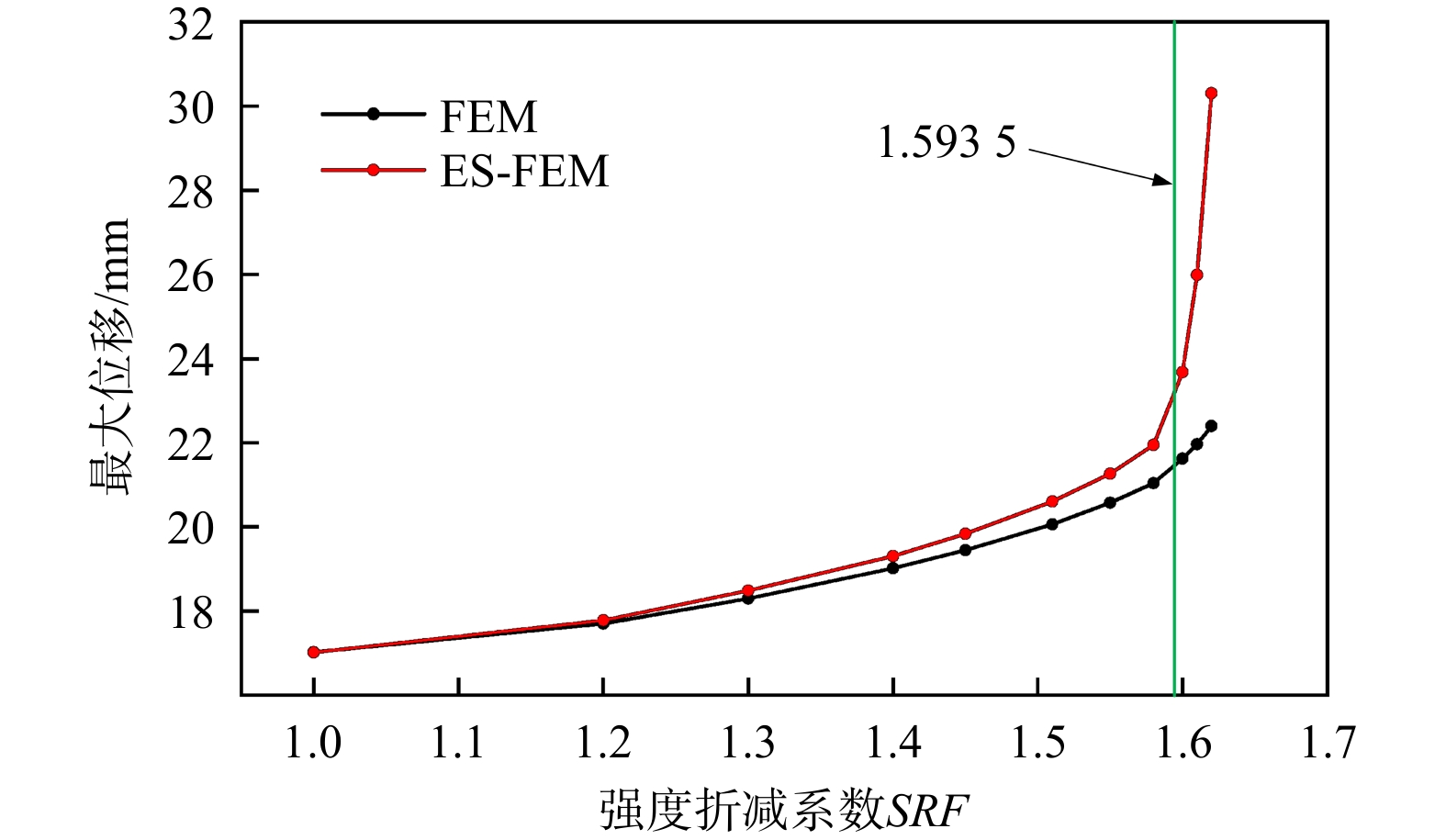
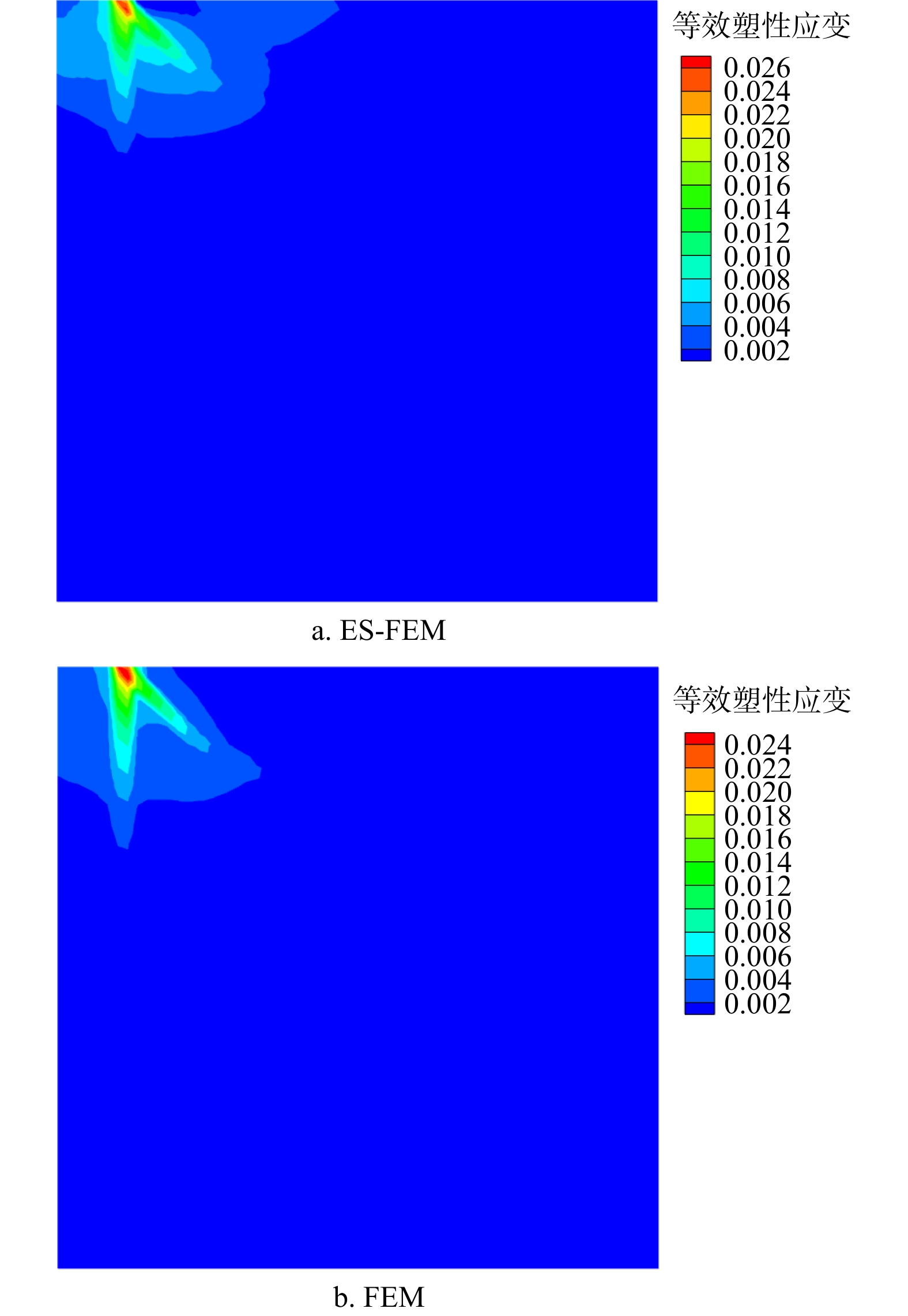
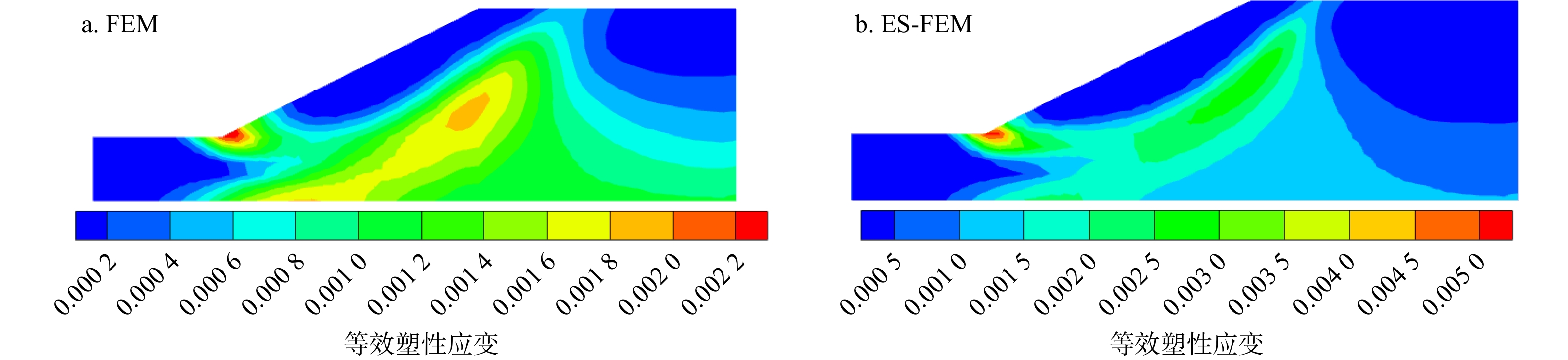
边坡的最大位移与强度折减系数的关系如图9所示（由于Morgenstern和Bishops法的结果极为接近，故在图中以二者均值1.5935为参考解），当$SRF \gt 1.58$后，ES-FEM法所求得边坡的最大位移急剧增大，同时FEM法求得的边坡位移既有增大的趋势也有一定增长。$SRF = 1.6$时的等效塑性应变分布如图10所示，ES-FEM和FEM求得的边坡塑性区都已基本贯通，且ES-FEM的塑性应变明显大于FEM，更符合塑性区贯通后，塑性应变快速增长的特征，说明采用ES-FEM法在$SRF = 1.6$之前就已达到极限状态，而FEM在$SRF = 1.6$时初步达到极限状态，ES-FEM与参考解更为吻合。综合位移和塑性应变的状态，推测安全系数应当在1.58到1.6之间，与参考解较为吻合。

图  9  边坡最大位移与强度折减系数的关系

Figure  9.  Relationship between the maximum displacement of the slope and the strength reduction coefficient

下载: 全尺寸图片 幻灯片

图  10  强度折减系数$S R F = 1.6$时的等效塑性应变分布

Figure  10.  Distribution of the equivalent plastic strain with $S R F = 1.6$

下载: 全尺寸图片 幻灯片

5.   结论

（1）在经典的条形基础承载力模型和边坡模型中，ES-FEM所取得的数值解均与参考解具有极高的吻合度。在条形基础承载力模型中，ES-FEM在自由度3362的状态下，结果与参考解相比误差仅为0.24%；在边坡模型中，ES-FEM在安全系数为1.59附近，边坡最大位移有明显的快速增长，符合实际塑性模型的发展趋势，验证了本研究算法的可行性和实用性，证明ES-FEM可以作为一种有效求解岩土工程问题的数值算法。

（2）在条形基础承载力模型中，通过比较在不同网格状态下ES-FEM和FEM求得的承载力系数，不仅证明了ES-FEM在相同网格状态下计算精度要显著高于FEM，而且证明了ES-FEM采用较为稀疏的网格状态便能取得符合精度需求的解。

所有作者声明不存在利益冲突。

The authors declare that no competing interests exist.